基爾霍夫的電流定律（KCL）是基爾霍夫的第一個(gè)定律，用于處理進(jìn)入和離開結(jié)的電荷守恒。

確定電流周圍的電流量或大小或電子電路，我們需要使用某些法律或規(guī)則，允許我們以等式的形式記下這些電流。所使用的網(wǎng)絡(luò)方程式是根據(jù)基爾霍夫定律的方程式，當(dāng)我們處理電路電流時(shí)，我們將研究基爾霍夫的當(dāng)前定律（KCL）。

Gustav Kirchhoff的現(xiàn)行定律是用于電路分析的基本定律之一。他的現(xiàn)行法律規(guī)定，對(duì)于并聯(lián)路徑，進(jìn)入電路結(jié)的總電流恰好等于離開相同結(jié)的總電流。這是因?yàn)樗鼪]有其他地方可以去，因?yàn)闆]有電荷丟失。

換句話說(shuō)，所有進(jìn)入和離開結(jié)點(diǎn)的電流的代數(shù)和必須等于零：ΣI IN =ΣI OUT 。

基爾霍夫的這個(gè)想法通常被稱為充電守恒，因?yàn)殡娏髟诮Y(jié)點(diǎn)周圍保守而沒有電流損失。讓我們看一下Kirchhoff當(dāng)前定律（KCL）應(yīng)用于單個(gè)連接點(diǎn)的簡(jiǎn)單示例。

單個(gè)連接點(diǎn)

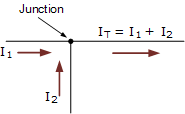
這個(gè)簡(jiǎn)單的單結(jié)示例中，離開結(jié)點(diǎn)的電流 I T 是兩個(gè)電流的代數(shù)和， I 1 和 I 2 進(jìn)入同一個(gè)交叉點(diǎn)。那是 I T = I 1 + I 2 。

請(qǐng)注意我們可以也正確地將其寫為代數(shù)和： I T - （I 1 + I 2 ）= 0 。

所以，如果我 1 等于3安培且I 2 等于2安培，那么總電流I T 離開結(jié)點(diǎn)將是3 + 2 = 5安培，我們可以將此基本定律用于任意數(shù)量的結(jié)點(diǎn)或節(jié)點(diǎn)，因?yàn)檫M(jìn)入和離開的電流總和將相同。

此外，如果我們顛倒了電流的方向，對(duì)于I 1 或I 2 ，得到的方程仍然適用。當(dāng)我 1 = I T -I 2 = 5-2 = 3安培，I 2 = I T -I 1 = 5-3 = 2安培。因此，我們可以將進(jìn)入結(jié)點(diǎn)的電流視為正（+），而離開結(jié)點(diǎn)的電流為負(fù)（ - ）。

然后我們可以看到電流的數(shù)學(xué)總和要么進(jìn)入或者離開交叉點(diǎn)并且在任何方向上總是等于零，這形成了基爾霍夫連接規(guī)則的基礎(chǔ)，更常見的是基爾霍夫的當(dāng)前定律或（KCL）。

并聯(lián)電阻

讓我們看看我們?nèi)绾螌irchhoff的電流定律并聯(lián)應(yīng)用于電阻，無(wú)論這些分支中的電阻是相等還是不相等。請(qǐng)考慮以下電路圖：

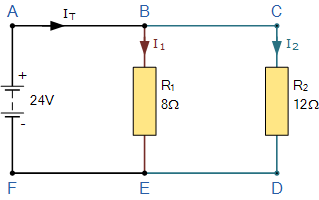
在這個(gè)簡(jiǎn)單的并聯(lián)電阻器示例中，有兩個(gè)不同的電流結(jié)。結(jié)點(diǎn)1發(fā)生在節(jié)點(diǎn)B處，結(jié)點(diǎn)2發(fā)生在節(jié)點(diǎn)E處。因此，我們可以使用基爾霍夫結(jié)點(diǎn)規(guī)則來(lái)處理這兩個(gè)不同結(jié)點(diǎn)的電流，對(duì)于那些進(jìn)入結(jié)點(diǎn)的電流以及流向結(jié)點(diǎn)的電流。 / p>

首先，所有電流，I T 離開24伏電源并到達(dá)A點(diǎn)，然后從那里進(jìn)入節(jié)點(diǎn)B.節(jié)點(diǎn)B是一個(gè)結(jié)，因?yàn)殡娏鳜F(xiàn)在可以分成兩個(gè)不同的方向，一些電流向下流動(dòng)并通過(guò)電阻器R 1 ，其余部分繼續(xù)通過(guò)電阻器R 2 通過(guò)節(jié)點(diǎn)C繼續(xù)。注意電流流動(dòng)進(jìn)入和離開節(jié)點(diǎn)通常稱為分支電流。

我們可以使用歐姆定律來(lái)確定通過(guò)每個(gè)電阻的各個(gè)分支電流：I = V / R，因此：

對(duì)于電流分支B至E，通過(guò)電阻R 1

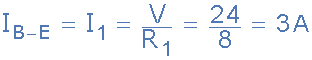
對(duì)于電流分支C至D通過(guò)電阻R <子> 2

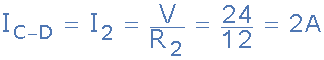
從上面我們知道基爾霍夫的現(xiàn)行定律表明，進(jìn)入結(jié)的電流之和必須等于離開結(jié)的電流之和，在上面的簡(jiǎn)單例子中，有一個(gè)電流I T 進(jìn)入節(jié)點(diǎn)B的結(jié)點(diǎn)，兩個(gè)電流離開結(jié)點(diǎn)，I 1 ，I 2 。

由于我們現(xiàn)在從計(jì)算中知道離開節(jié)點(diǎn)B處的結(jié)的電流是I 1 等于3安培而I 2 等于2安培，進(jìn)入節(jié)點(diǎn)B的結(jié)點(diǎn)的電流必須等于3 + 2 = 5安培。因此Σ IN = I T = 5安培。

在我們的例子中，我們?cè)诠?jié)點(diǎn)B和節(jié)點(diǎn)E有兩個(gè)不同的連接點(diǎn)，因此我們可以確認(rèn)I T 的這個(gè)值，因?yàn)閮蓚€(gè)電流在節(jié)點(diǎn)E再次重新組合。因此，對(duì)于Kirchhoff的連接規(guī)則保持為真，進(jìn)入F點(diǎn)的電流之和必須等于流出的電流之和節(jié)點(diǎn)E的連接點(diǎn)。

由于進(jìn)入結(jié)E的兩個(gè)電流分別為3安培和2安培，因此進(jìn)入F點(diǎn)的電流之和為：3 + 2 = 5安培。因此Σ IN = I T = 5安培，因此基爾霍夫電流定律成立，因?yàn)樗c當(dāng)前離開點(diǎn)A的值相同。

將KCL應(yīng)用于更復(fù)雜的電路。

我們可以使用基爾霍夫電流定律來(lái)找到在更復(fù)雜電路周圍流動(dòng)的電流。我們希望現(xiàn)在知道節(jié)點(diǎn)（連接點(diǎn)）處的所有電流的代數(shù)和等于零，并且考慮到這個(gè)想法，這是確定進(jìn)入節(jié)點(diǎn)和離開節(jié)點(diǎn)的電流的簡(jiǎn)單情況。考慮下面的電路。

基爾霍夫的現(xiàn)行法律例子No1

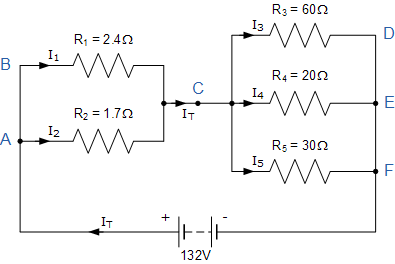
在這個(gè)例子中是電流在節(jié)點(diǎn)A，C，E和節(jié)點(diǎn)F處分開或合并在一起的四個(gè)不同的結(jié)點(diǎn)。電源電流I T 在流過(guò)電阻器R 1 和R 2 ，在節(jié)點(diǎn)C重新組合，然后再次通過(guò)電阻器R 3 ，R 4 和R 5 分離最后在節(jié)點(diǎn)F再次重新組合。

但在我們計(jì)算流過(guò)每個(gè)電阻支路的各個(gè)電流之前，我們必須首先計(jì)算電路總電流I T 。歐姆定律告訴我們I = V / R并且我們知道V的值，132伏，我們需要計(jì)算電路電阻如下。

電路電阻R AC

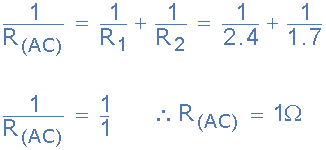
因此節(jié)點(diǎn)A和C之間的等效電路電阻計(jì)算為1歐姆。

電路電阻R CF

>

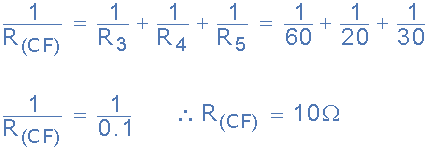
因此節(jié)點(diǎn)C之間的等效電路電阻并且F計(jì)算為10歐姆。然后總電路電流I T 給出如下：

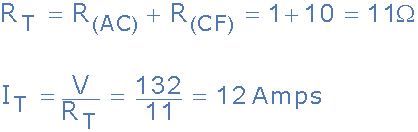
給我們一個(gè)等效電路：

基爾霍夫電流定律等效電路

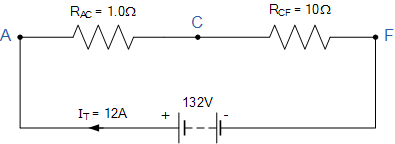
因此，V = 132V，R AC =1Ω，R CF =10Ω，I T = 12A。

建立等效并聯(lián)電阻和電源電流后，我們可以現(xiàn)在計(jì)算各個(gè)分支電流并使用Kirchhoff的連接規(guī)則確認(rèn)如下。

因此，我 1 = 5A，I 2 = 7A，I 3 = 2A，I 4 = 6A，I 5 = 4A。

我們可以通過(guò)使用節(jié)點(diǎn)C作為我們的參考點(diǎn)來(lái)計(jì)算進(jìn)入和離開結(jié)點(diǎn)的電流，確認(rèn)Kirchoff的電流定律適用于電路：

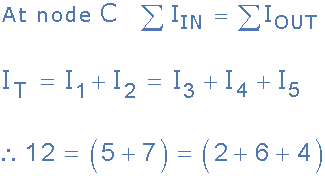
我們還可以仔細(xì)檢查Kirchhoffs Current Law是否適用，因?yàn)檫M(jìn)入交叉點(diǎn)的電流是正的，而離開的是周四，路口是負(fù)面的代數(shù)和是：I 1 + I 2 -I 3 -I 4 -I 5 = 0等于5 + 7 - 2 - 6 - 4 = 0.

因此我們可以通過(guò)分析證實(shí)基爾霍夫電流定律（KCL）表明電流的代數(shù)和在這個(gè)例子中，電路網(wǎng)絡(luò)中的連接點(diǎn)始終為零是正確的。

基爾霍夫電流定律示例No2

使用基爾霍夫電流定律求出在后續(xù)電路周圍流動(dòng)的電流僅

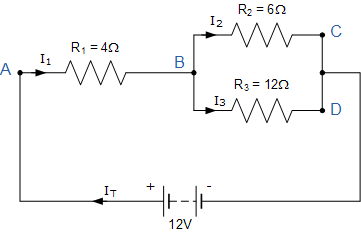
I T 是由12V電源電壓驅(qū)動(dòng)的電路周圍的總電流。在A點(diǎn)， I 1 等于 I T ，因此會(huì)有 I 1 * R 電阻R 1 上的電壓降。

該電路有2個(gè)分支，3個(gè)節(jié)點(diǎn)（B，C和D）和2個(gè)獨(dú)立的循環(huán)，因此兩個(gè)循環(huán)周圍的I * R電壓降將是：

循環(huán)ABC?12= 4I 1 + 6I 2

循環(huán)ABD?12= 4I 1 + 12I 3

由于基爾霍夫現(xiàn)行法律規(guī)定在節(jié)點(diǎn)B處， I 1 = I 2 + I 3 ，因此我們可以用兩個(gè)當(dāng)前的I 1 代替（I 2 + I 3 ）跟隨循環(huán)方程，然后簡(jiǎn)化。

基爾霍夫環(huán)路方程

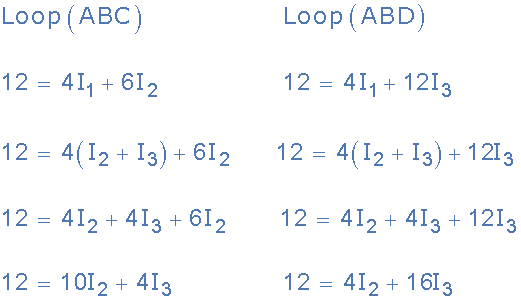
我們現(xiàn)在有兩個(gè)與在電路周圍流動(dòng)的電流有關(guān)的聯(lián)立方程。

Eq。否1： 12 = 10I 2 + 4I 3

等式No 2： 12 = 4I 2 + 16I 3

將第一個(gè)等式（循環(huán)ABC）乘以4并且從循環(huán)ABC中減去Loop ABD，我們可以減少這兩個(gè)方程，得到 I 2 和 I 3 的值

等式否1： 12 = 10I 2 + 4I 3 （x4）? 48 = 40I 2 + 16I <子> 3

等式No 2： 12 = 4I 2 + 16I 3 （x1）? 12 = 4I 2 + 16I <子> 3

等式?jīng)]有1-Eq。否2? 36 = 36I 2 +0

用術(shù)語(yǔ)替換 I 2 of I 3 為我們提供 I 2 的值為 1.0Amps

現(xiàn)在我們可以通過(guò)將第一個(gè)等式（循環(huán)ABC）乘以4和第二個(gè)等式（Loop）來(lái)執(zhí)行相同的過(guò)程來(lái)找到 I 3 的值再次通過(guò)從Loop ABD中減去Loop ABC，我們可以減少兩個(gè)方程，得到 I 2 和 I 的值3

等式否1： 12 = 10I 2 + 4I 3 （x4）? 48 = 40I 2 + 16I <子> 3

等式否2： 12 = 4I 2 + 16I 3 （x10）? 120 = 40I 2 + 160I <子> 3

等式?jīng)]有2-Eq。否1? 72 = 0 + 144I 3

因此替換 I 3 in術(shù)語(yǔ) I 2 為我們提供 I 3 的值為 0.5Amps

正如Kirchhoff的交叉規(guī)則所述： I 1 = I 2 + I 3

流過(guò)電阻器 R 1 的電源電流如下： 1.0 + 0.5 = 1.5Amps

因此 I 1 = I T = 1.5Amps ， I 2 = 1.0Amps 和 I 3 = 0.5Amps 根據(jù)該信息，我們可以計(jì)算出器件和電路周圍各點(diǎn)（節(jié)點(diǎn)）的I * R壓降。

我們可以簡(jiǎn)單而簡(jiǎn)單地使用歐姆定律解決了示例二的電路，但我們?cè)谶@里使用基爾霍夫電流定律來(lái)說(shuō)明如何解決更復(fù)雜的電路當(dāng)我們不能簡(jiǎn)單地應(yīng)用歐姆定律時(shí)。