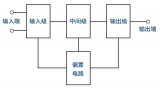
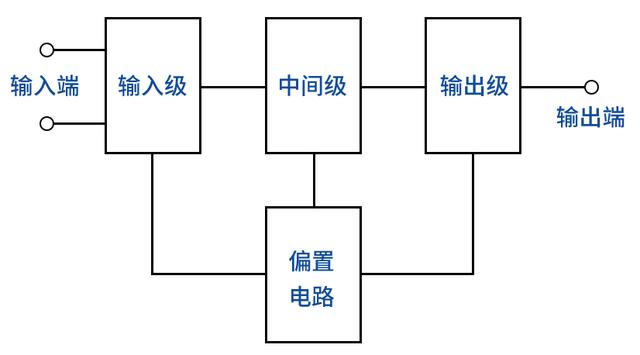
集成運算放大器
電子發(fā)燒友認(rèn)為半導(dǎo)體集成電路是以半導(dǎo)體硅單晶為基礎(chǔ)材料,以制造平面晶體管的平面工藝為基本工藝,將許多無、器件連同它們接線等制造在同一基片上,并能夠完成各種電功能的電子線路。它實現(xiàn)了材料、元器件、電路三者的有機組合,具備集成密度高、引線短、外部焊點少、成本低、可靠性高等優(yōu)點。
1、基本運算電路
集成電路按功能劃分,可分為數(shù)字和模擬兩大類。模擬集成電路用于模擬信號的產(chǎn)生和處理,其種類繁多,包括集成運算放大器、集成模擬乘法器、集成鎖相環(huán)、集成功率放大器、集成穩(wěn)壓電源、集成寬帶放大器、集成數(shù)模和模數(shù)轉(zhuǎn)換電路等。其中集成運放是技術(shù)功能的通用性最大、應(yīng)用最廣泛、以展最快、品種與數(shù)量最多的一種線性集成電路。
集成運放裨上是一種高增益直流放大、直流放大器既能放大變化極其緩慢的直流信號,下限頻率可到零;又能放大交流信號,上限頻率與普通放大器一樣,受限于電路中的電容或電感等電抗性元器件。集成運放和外部反饋網(wǎng)絡(luò)相配置后,能夠在它的輸出和輸入之間建立起種種特定的函數(shù)關(guān)系,故而稱它為“運算”放大器。
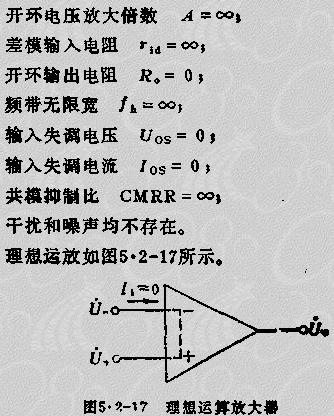
分析處于線性放大狀態(tài)的理想和實際運算放大器的基本依據(jù)是
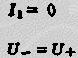
U-=U+也稱“虛短路”。對于實際的運算放大器,常常也可據(jù)此進行近似分析。
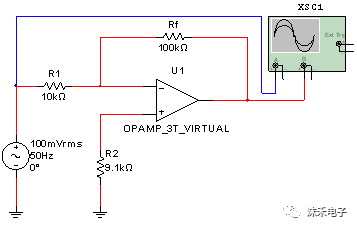
(1)反相運算放大器 圖5.2-18所示是運算放大器反相放大組態(tài)電路,通過反饋元件ZF構(gòu)成閉環(huán)。理想運算放大器反相放大閉環(huán)增益的基本關(guān)系式
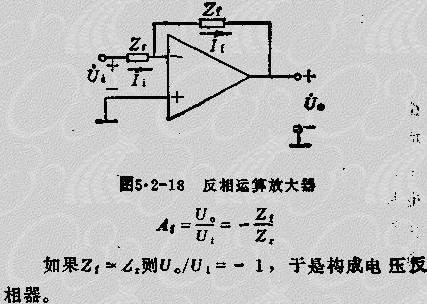
反相輸入端具有地電位,而并沒有真正接地之“虛地”點。
反相運算放大器的輸入阻抗為z1F=Z
反相放大組態(tài)實質(zhì)上是電壓并聯(lián)負(fù)反饋,具有輸入阻抗和輸出阻抗低的特點。
ZPZ為溫度補償元件,為了確保運算放大處于對稱平衡狀態(tài),應(yīng)使從反相輸入端和從同相輸入端賂外部看去的等效直流電阻相等,則元件選擇時應(yīng)使ZP=ZF//ZZ
如果用不同的電阻、電容網(wǎng)絡(luò)來構(gòu)成ZF、ZP,就能得到功能不同的各種反相運算電路。例如反相比例器、加法器、微分器、積分器、有源濾波器和有源校正電路等。下面僅舉反相加法器一例,如圖5.2-19所示電路。
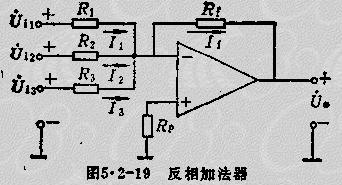
由于反相端為“虛地”,故三個輸入電壓彼此獨立地通過自身的輸入回路電阻,轉(zhuǎn)換成下列各式電流:
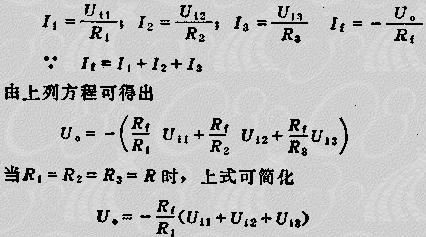
由此可見,當(dāng)運算放大器具有理想特性時,各相加項的比例因子僅與外電路電阻有關(guān),適當(dāng)選擇各電阻阻值,就能得到所需要的比例因子,因此這種加法電路可以達到很高的精度和穩(wěn)定性。加法運算呈現(xiàn)在各輸入電流在反相端相加。故稱反相端為“相加點”,或稱“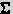 ”點。
”點。
補償電阻RP用于保證電路具有平衡對稱結(jié)構(gòu),其值應(yīng)選為RP=R1||R2||R3||RT
由于反相端為“虛地”,故對每個輸入信號而言,加法器的輸入電阻分別為輸入回路電阻R1、R2、R3。
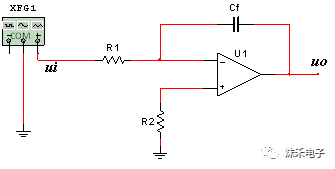
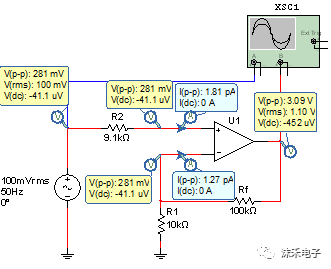
(2)同相運算放大器 圖5.2-20為運算放大器同相放大組態(tài)。
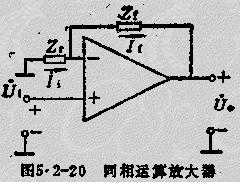
理想運算放大呂同相放大閉環(huán)增益的關(guān)系式:

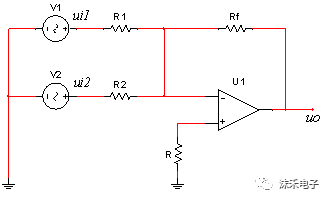
(3)差動放大器
1)基本差動放大器
將反相放大組態(tài)和同相放大組態(tài)二者結(jié)合起來,便構(gòu)成運算放大器的差運放大組態(tài),如圖5.2-21所示。
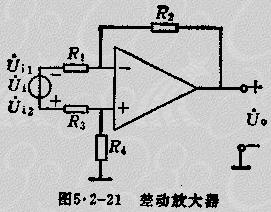
差動運放只對差模輸入信號實現(xiàn)運算,不反映共模輸入信號。對于理想運算放大器,若外部回路

差動放大器具有抑制零點漂移和抗干抗性等特點,所以應(yīng)用極為普遍。
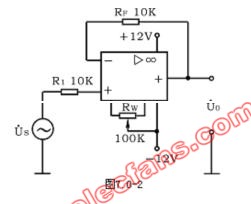
2)增益可調(diào)差動放大器 實際應(yīng)用中,通常要求增益可調(diào)。將基本差動放大器結(jié)構(gòu)適當(dāng)改變,就能實現(xiàn)用一個電位器調(diào)節(jié)增益的任務(wù),電路如圖5.2-22所示。該電路的閉環(huán)增益為
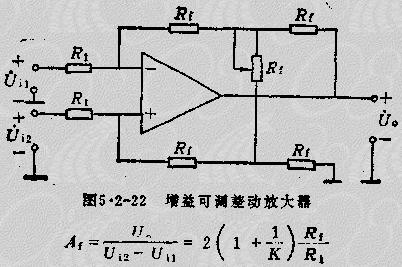
式中K為電位器的滑動比。
當(dāng)滑動端在圖示最上位置時,K=1;在最下位置時,K=0,通常在電位器支路串有一個固定電阻,以避免調(diào)節(jié)過程中出現(xiàn)過大增益,確保電路工作穩(wěn)定。這樣調(diào)節(jié)滑動比,增益A1就可以在很大范圍內(nèi)變化。此種增益調(diào)節(jié)電路簡單易實現(xiàn),且不影響電路的共扼抑制能力,缺點是增益調(diào)節(jié)特性是非線性的。
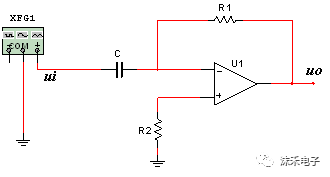
(4)積分器 基本積分器電路圖如5.2-23。其輸入回中元件為電阻,反饋回路元件為電容,屬于反相運算電路。

基本積分器能否實現(xiàn)精確積分運算的關(guān)鍵在于反相端是否為“虛地”,不論什么原因使反相端偏離“虛地”,都將引起積分運算誤差。
差動積分器,可由兩個運算放大組成,電路性能較好,如圖5.2-24所示。
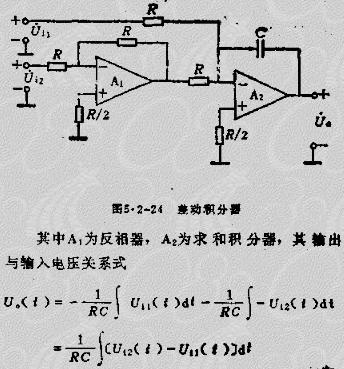
此電路完全避免兩個差動信號分別積分時,要求工作狀態(tài)的一致性。
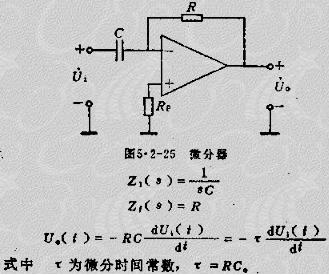
(5)微分器 微分器用來對輸入信號實現(xiàn)微分運算,因為微分是積分的逆運算,所將積分器的輸入回路電阻與反饋回路電容位置相互對換,就構(gòu)成微分器。基本微分電路如圖5.2-25所示。其輸入回路元器為電容,反饋回路元件為電阻,即
(6)對數(shù)與反對數(shù)運算電路 對數(shù)與反對數(shù)運算電路是對輸入信號實行對數(shù)或指數(shù)運算,它們是一類非線性函數(shù)運算電路。對它們進行適當(dāng)組合,可構(gòu)成乘法、除法、乘方和開方等各種非線性運算電路。
1)對數(shù)運算電路 實際應(yīng)用中,將晶體三極管接在反相放大器的反饋支路代替電阻,則構(gòu)成對數(shù)運算電路,如圖5.2-26所示。

即輸出電壓完成對輸入電壓的對數(shù)運算。
2)反對數(shù)運算電路 將基極和集電極短接的晶體三極管接在反相放大器的輸入回路中,就構(gòu)成了反對數(shù)運算放大器,電原理電路如圖5.2-27所示。

即輸出電壓完成對輸入電壓的反對數(shù)運算。
對數(shù)運算電路與反對數(shù)運算電路存在相同問題,即運算精度溫度影響較大,實際應(yīng)用中都必須進行溫度補償。
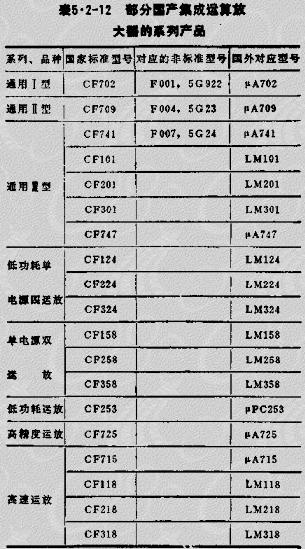
2、部分國產(chǎn)集成運算放大器的系列(見表5.2-12)
 電子發(fā)燒友App
電子發(fā)燒友App










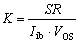










評論