結合傳統的混沌映射，提出一種組合式混沌映射模型。給出了產生新的混沌擴頻序列的方法。首先由給定初值代入組合式混沌映射進行迭代，并且通過隨機的參數切換選擇不同的組合混沌映射，再將迭代產生的序列進行預處理，最后將預處理后的序列進行L比特選擇得到新的混沌擴頻序列。對得到的混沌擴頻序列進行平衡性、保密性和相關性分析，并與現有的混沌擴頻序列的性能進行比較。結果表明，該混沌擴頻序列具有與現有的混沌擴頻序列相近的相關性，而且其平衡性、保密性更好。

　　個擴頻通信系統的性能優劣在很大程度上取決于所選擴頻序列的性能，而混沌擴頻序列在很多方面具有傳統擴頻序列無法比擬的優勢，例如初值敏感性、類噪聲性、非周期性等，使其非常適合于擴頻通信系統。

　　對Logistic混沌擴頻序列進行了改進，提出該序列具有很好的擴頻特性； 對Chebyshev混沌映射的量化進行了改進，體現了很好的偽隨機性能。雖然典型的混沌擴頻序列及其改進序列在很多方面都具有很好的性能，但是存在復雜度不高、保密性不理想的缺陷。針對典型的混沌擴頻序列存在的保密性不理想的問題，提出了一種在改進型Logistic混沌映射和Chebyshev混沌映射基礎上構建的組合混沌映射，并指出該混沌擴頻序列具有與Logistic混沌擴頻序列相近的良好性能，而且保密性更好。但是給出的利用符號函數產生混沌擴頻序列的方法復雜度較低，嚴重影響其抗破譯能力。本文針對的混沌擴頻序列存在的不足，提出了一種新的組合混沌映射模型，并給出了可以提高抗破譯能力的混沌擴頻序列的產生方法。仿真結果表明，本文提出的混沌擴頻序列具有更好的平衡性和保密性。

　　1組合式混沌映射模型

　　結合傳統的Logistic 型、改進Logistic 型、Chebyshev型混沌映射，本文給出一一種組合式混沌映射模型，其數

　　學表達式為：

　　（1）xn+1= b + b2cos （4cos ‘x ）+ b 3xn- b4xn

　　式中b.b2、bs、b4 稱為組合系數。

　　結合傳統的Logistic 型、改進Logistic 型、Chebyshev型混沌映射的特點，組合系數矩陣b 的具體取值為：當

　　b;=0，bz=0，b3=r，ba=r 時，為Logistic 型混沌映射;當bp=1，

　　bz=0，b3=0，ba=2 時，為改進Logistic 型混沌映射;當bp=0，

　　b2=1，bz=0，ba=0 時，為Chebyshev 型混沌映射，其中r 的取值范圍為re［1，4］。

　　指出，Chebyshev 型混沌映射都是傳統Logistic 型的函數變換，所以將三種混沌映射進行組合后的混沌映射模型在本質上與三種混沌映射是一致的。

　　2. 混映頻定外的產告

　　由于混沌序列在理想情況下是非周期的圖1，將其應用到擴頻通信系繞中時，需要截取其中的一段，截短后的序列的相關性能不會發生變化。并且混沌實值序列不能直接應用到現有的數字擴頻通信系統中，需對其進行數字化得到二進制序列。

　　假設需要得到混沌擴頻序列的總長度為K，擴頻用戶數為M，產生混沌擴頻序列的具體步驟為：

　　（1）由給定初值的前提下，將其代入組合式混沌映

　　射進行M次迭代，設迭代產生的混沌擴頻序列為，xn..*.x.且xe （-1，1）;

　　（2）將迭代產生的混沌序列進行預處理，使得預處理后的序列ye（0，1），便于后續的數字化處理，預處理的方法如下：

　　yi=（xi+1）/2

　　（3 ）將序列y 表示為二進制形式，y=0.k1，k2其中kj=0或1。在產生的二進制序列中再進行比特選擇，選擇L位比特的序列，例如從j=Ll 開始（L1為L的起始位），得到的序列為：kuku.iun.L 的大小取決于K/M

　　值得渺意的是，在將給定初值代入組合式混沌映射模型中是行送股舒T岢以展鋸不世的組答紫數進行參數切換，而W參4V的實你naA所很多外因擇，可以采用等距離參數切換，也可以采用不等距的參數切換，還可以進行隨機的參數切換［81。從提高序列保密性的角度考慮，本文采用了隨機的參數切換。參數切換的具體步驟為：

　　（1）由于有3 種混沌映射可以選擇，故可以產生2-l=7種不同的參數切換情況，如表1所示。表1中“A”

　　表示Logistic 型混沌映射，“B”表示改進Logistic 型混沌映射。

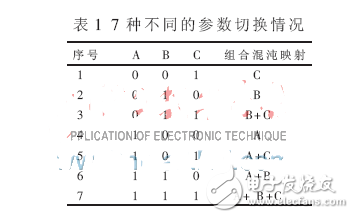
　　（2）序號為1、2、4的三種情況下，組合混沌映射即為三種典型的混沌映射中的一種，且迭代產生的序列的取值范圍一定滿足xi∈（-1，1）；

　　（3）序號為3、5、6、7的四種情況下，組合混沌映射為三種典型的混沌映射的不同組合，其迭代產生的序列的取值范圍不一定滿足xi∈（-1，1），此時就需要進行閾值判斷，也即，如果序列的取值不在（-1，1）范圍內就舍棄，如果在（-1，1）范圍內就保留。

　　（4）在給定初值進行迭代時， 7種不同的參數切換情況隨機地進行選擇。

　　該方法得到的混沌擴頻序列的優勢主要體現在：

　　（1）先根據擴頻用戶數確定迭代的序列長度，大大減少了運算量；

　　（2）將給定初值代入式（1）進行迭代時可以根據不同的組合系數進行參數切換，相比傳統的單一混沌映射，可以提高序列的保密性；

　　（3）在進行L比特選擇的時候，起始位L1可以隨機產生，進一步提高了序列的保密性。

　　2 混沌擴頻序列性能分析

　　2.1平衡性分析

　　在擴頻通信系統中，擴頻序列的平衡性與載波抑制度有密切關系，且不平衡的序列會使系統載波泄露大，易出現誤碼或信息丟失，故混沌擴頻序列的平衡性對擴頻通信系統有非常重要的意義。用P和Q分別表示混沌擴頻序列中“0”和“1”的個數，則序列的平衡度可以表示為：

　　E=|P-Q|/K （3）

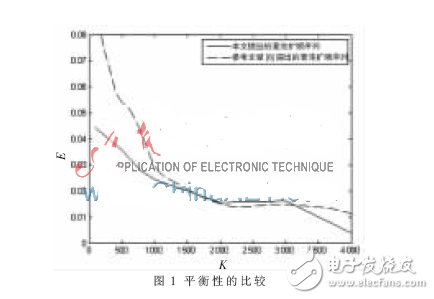
　　將本文的混沌擴頻序列的平衡性與中給出的混沌擴頻序列的平衡性進行比較，結果如圖1所示，圖1中用實線表示本文提出的混沌擴頻序列的平衡度，虛線表示提出的混沌擴頻序列的平衡度。從圖1中很直觀地可以看出，本文提出的混沌擴頻序列的平衡性優于現有的混沌擴頻序列的平衡性。

　　2.2 保密性分析

　　本文提出的混沌擴頻序列在的基礎上對保密性進行了提高，主要體現在三個方面：

　　（1）給出了7種參數切換的隨機選擇情況；

　　（2）混沌擴頻序列的產生方法從整體上優于給出的方法，僅僅通過符號函數將混沌實值序列變換為混沌數字化序列；

　　（3）采用的L位的比特選擇，其起始位可以隨機產生。圖2中給出利用本方法產生的混沌擴頻序列的一個例子，假設序列長度為900，初值為0.123 4。

　　2.3 相關性分析

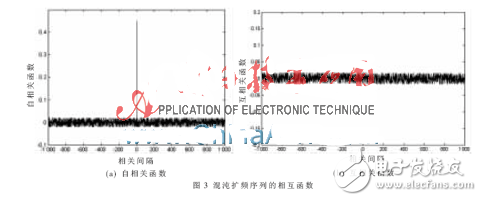
　　根據序列的自相關函數和互相關函數的定義，可以得出本文提出的混沌擴頻序列的相關性，如圖3所示。其中圖3（a）表示初值為0.345 6、序列長度為2 000的混沌擴頻序列的自相關函數隨相關間隔的變化情況，相關間隔的取值范圍為-1 000~1 000。從圖3（a）中可以看出，當m=0時，自相關函數值為0.46，自相關旁瓣接近0，仿真結果表明該混沌擴頻序列具有很好的自相關性。 圖3（b）表示兩個不同的混沌擴頻序列的互相關函數隨相關間隔的變化情況，互相關值也很小，接近于0。從圖3中可以看出，本文提出的混沌擴頻序列與的序列的相關性相近。

　　本文提出一種組合式混沌映射模型，該模型結合了現有的三種典型的混沌映射，包括：Logistic型、改進Logistic型和Chebyshev型混沌映射。同時提出了產生混沌擴頻序列的方法，該方法在給定初值的前提下進行迭代，迭代時可以根據7種不同組合的系數進行隨機的參數切換。再將序列進行預處理，預處理后的序列再進行L比特選擇，其中所選擇的L位序列的起始位L1可以隨機產生，進一步提高該序列的保密性。將本文提出的混沌擴頻序列的平衡性給出的序列的平衡性進行比較，仿真結果表明，本文的序列的平衡性優于現有序列的平衡性。本文提出的混沌擴頻序列的產生方法從多個角度提高了序列的保密性，包括隨機的7種參數切換、L位的比特選擇，相比具有更好的保密性。并對該混沌擴頻序列的相關性進行了分析，仿真結果表明與現有序列的相關性相當。新的混沌擴頻序列的產生方法的提出，為混沌序列在擴頻通信系統中的應用奠定了堅實的理論基礎。