什么是AD轉換?
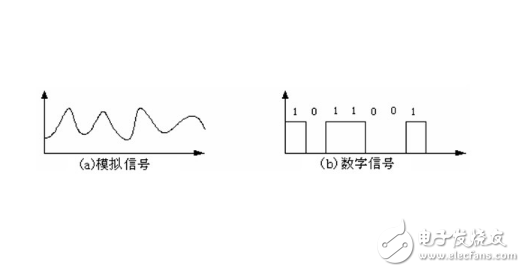
AD轉換就是模數轉換。顧名思義,就是把模擬信號轉換成數字信號。主要包括積分型、逐次逼近型、并行比較型/串并行型、Σ-Δ調制型、電容陣列逐次比較型及壓頻變換型。
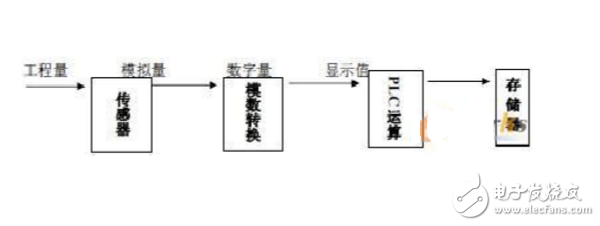
A/D轉換器是用來通過一定的電路將模擬量轉變為數字量。模擬量可以是電壓、電流等電信號,也可以是壓力、溫度、濕度、位移、聲音等非電信號。但在A/D轉換前,輸入到A/D轉換器的輸入信號必須經各種傳感器把各種物理量轉換成電壓信號。
信號采樣概念
信號采樣也稱抽樣(sample),是連續信號在時間上的離散化,即按照一定時間間隔△t 在模擬信號x(t)上逐點采取其瞬。
時值。它是通過采樣脈沖和模擬信號相乘來實現的。
采樣間隔的選擇和信號混淆:對模擬信號采樣首先要確定采樣間隔。如何合理選擇△t 涉及到許多需要考慮的技術因素。一般而言,采樣頻率越高,采樣點數就越密,所得離散信號就越逼近于原信號。
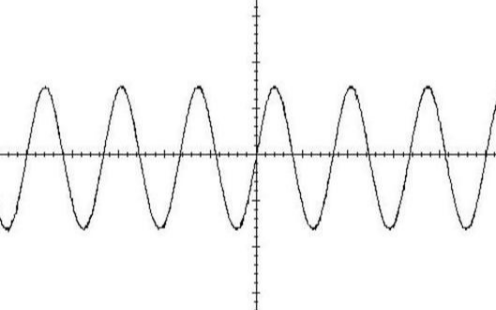
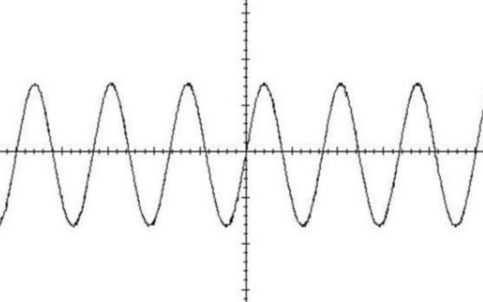
但過高的采樣頻率并不可取,對固定長度(T)的信號,采集到過大的數據量(N=T/△t),給計算機增加不必要的計算工作量和存儲空間;若數據量(N)限定,則采樣時間過短,會導致一些數據信息被排斥在外。采樣頻率過低,采樣點間隔過遠,則離散信號不足以反映原有信號波形特征,無法使信號復原,造成信號混淆。直觀地說信號混迭是把本該是高頻的信號誤認為低頻信號。
根據采樣定理可以得到,當采樣頻率大于原信號中最大組成頻率的兩倍時,可以比較好的還原信號,若小于最大組成頻率的兩倍則為欠采樣,會出現信號混疊現象。
模擬信號采樣與AD轉換
1 著名的Nyquist采樣定理
盡管大家都知道,但還是提一提。大牛奧本海姆的《信號與系統》中是這樣描述的:
Let x(t) be a band-limited signal with X(jw) = 0 for |w|》 wM. Then x(t) is uniquely determined by its samples x(nT),n=1,±1,±2,。。。,if
ws 》 2wM where ws = 2 pi/T.
Given these samples, we can reconstruct x(t) by generating a periodic impluse train in which successive impluse have amplitudes that are successive sample values. This impluse train is then processed through an ideal lowpass filter with gain T and cutoff frequency greater than wM and less than ws-wM. The resulting output signal will exactly equal x(t)。
來捋一捋,幾個點:
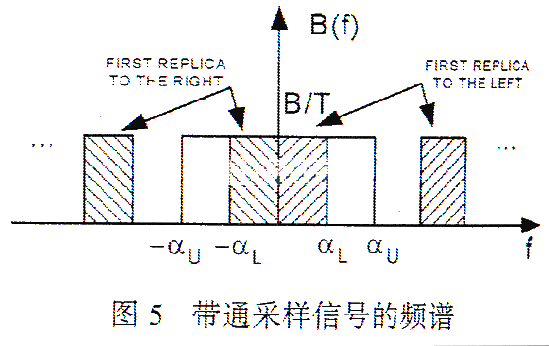
帶寬有限(band-limited)
采樣頻率大于2倍信號最高頻率后可以無失真的恢復出原始信號
實際中,信號往往是無線帶寬的,如何保證帶寬有限?所以,我們在模擬信號輸入端要加一個低通濾波器,使信號變成帶寬有限,再使用2.5~3倍的最高信號頻率進行采樣。關于此我們下面將模擬數字轉換過程將會看到。
雖說是不能小于等于2倍,但選2倍是不是很好呢,理論上,選擇的采樣頻率越高,越能無失真的恢復原信號,但采樣頻率越高,對后端數字系統的處理速度和存儲要求也就越高,因此要選擇一個折中的值。
如果后端數字信號處理中的窗口選擇過窄,采樣率太高,在一個窗口內很難容納甚至信號的一個周期,這從某方面使得信號無法辨識。比如,數字信號處理的窗口大小為1024個點,采樣率為50KHz,則窗口最多容納1024*(1/50KHz)=20.48ms的信號長度,若信號的一個周期為30ms》20.48ms,這就使得數字信號的處理窗口沒法容納一個周期信號,解決的辦法就是在滿足要求的前提下使用減小采樣率或增加窗口長度。
2 模數轉換
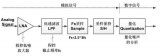
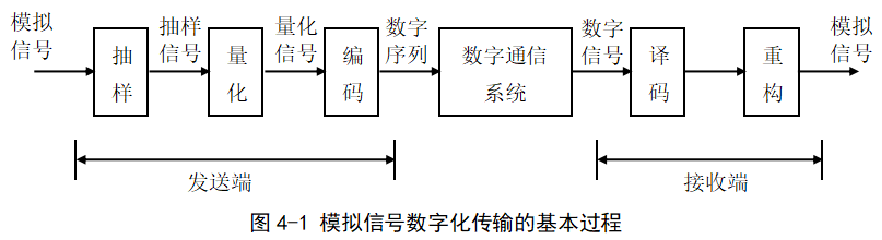
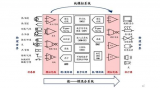
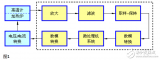
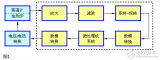
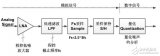
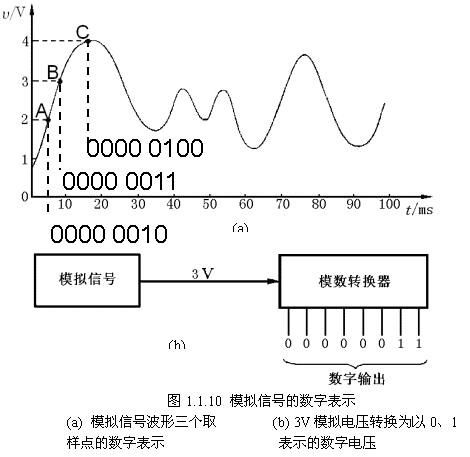
記得有一次參加中科院計算所的實習筆試,里面就有這么一道題:模擬信號轉換到數字信號要經歷哪兩個步驟?還好,早有準備,立刻填上了采樣和量化。我們下面就來詳細分析下這兩個過程,但在分析之前,我們先給出一張整個過程的流圖,您可以先想想為什么需要各模塊。
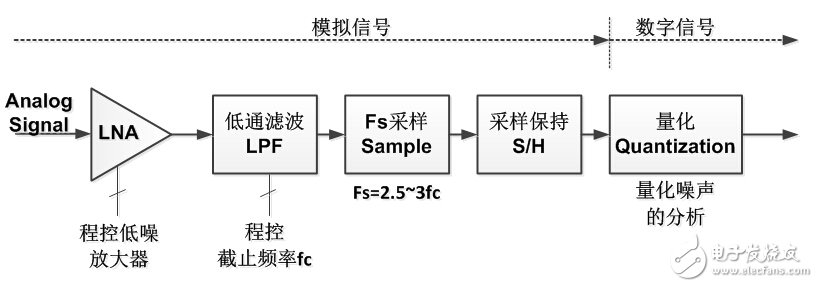
程控放大器
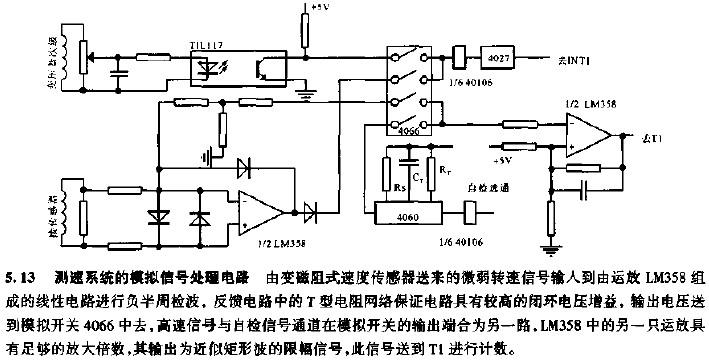
我們實際中的模擬信號都是通過傳感器采集進來的,做過單片機的人應該熟知DS18B20溫度傳感器,不好意思,那是數字傳感器,也就是說人家做傳感器的時候把AD轉換也放到傳感器里面了。但這并不是普遍的情況,因為溫度量是模擬信號中最容易測量的量了,而大多數的傳感器并沒有集成AD轉換過程,如大多數的加速度傳感器、震動傳感器、聲音傳感器、電子羅盤,甚至有的GPS(別懵了,GPS也算是一種傳感器哦)等,都是模擬輸出的。而且由于物理制作的原因,傳感器返回的電信號非常微小,一般在幾mV(如果是電流,也一般在幾mA),這么微弱的信號,如果經過導線或電纜傳輸很容易就湮滅在噪聲中。因此,我們常常見到模擬傳感器的輸出線都會使用套上一層塑膠的線,叫屏蔽線(如圖)。
屏蔽線只能保證在信號傳輸到系統之前受到的干擾最小,但信號仍要經過處理才能為數字系統使用。在模擬信號(尤其是高頻信號)的輸入端首先要使用低噪聲放大器對信號進行放大,這個放大器有特殊的要求,一定是低噪聲,我們已經知道,模擬信號信號已經非常微弱,如果放大器還存在一定的噪聲,在噪聲疊加之后放大出來的信號可能已經不再是原信號了。既然說到低噪聲,那么低噪聲是如何衡量的呢?這可以通過放大器噪聲系數(NF)來定,
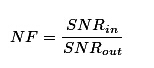
噪聲系數定義為放大器輸入信號與輸出信號的信噪比。其物理含義是:信號通過放大器之后,由于放大器產生噪聲,使信噪比變壞;信噪比下降的倍數就是噪聲系數。噪聲系數通常用dB表示,
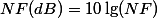
實際中除了考慮低噪聲系數外,還要考慮放大器的帶寬和頻率范圍以及最重要的放大增益。由于輸入信號的強度可能時變,采用程序可控(程控)的放大增益保證信號能達到滿度而又不會出現飽和(實際中要做到這一點還是很難的)。
低通濾波器
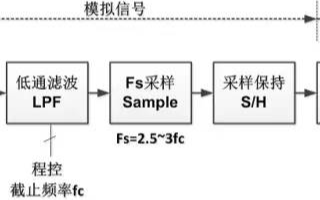
在Nyquist采樣定理中已經提過,要滿足采樣定理必須要求信號帶寬有限,使用大于2倍的最高信號頻率采樣才能保證信號的不混疊。低通濾波器的一個考慮就是使信號帶寬有限,以便于后期的信號采樣,這個低通濾波器是硬件實現的。另一方面,實際情況中我們也只會對某個頻頻段的信號感興趣,低通濾波器的另一個考慮就是濾波得到感興趣的信號。比如,測量汽車聲音信號,其頻率大部分在5KHz以下,我們則可以設置低通濾波器的截止頻率在7KHz左右。
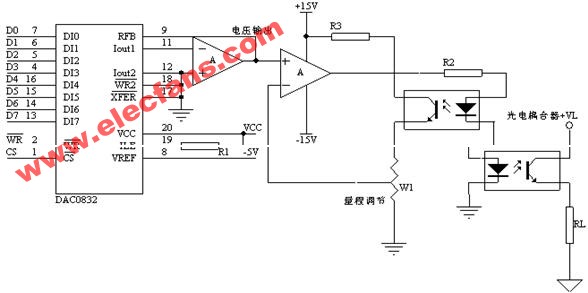
程控的實現方法就是使用模擬通道選擇芯片(如74VHC4051等)。
NOTES:
在采樣之前的所有電路實現方案叫信號調理電路。這樣,我們就可以根據這個詞到處Google/Baidu文獻了。
 電子發燒友App
電子發燒友App















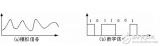
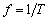










評論