波特圖應用
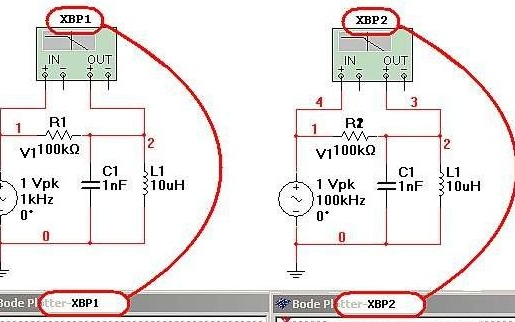
現在以一簡單的低通濾波器來窺探下波特圖的魅力。
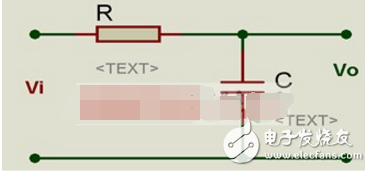
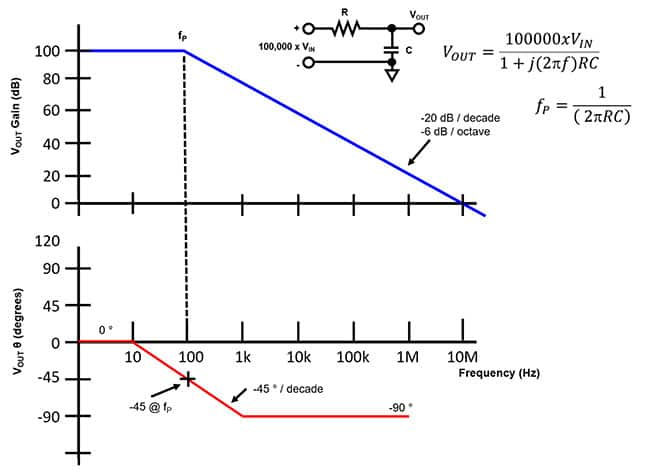
傳遞函數

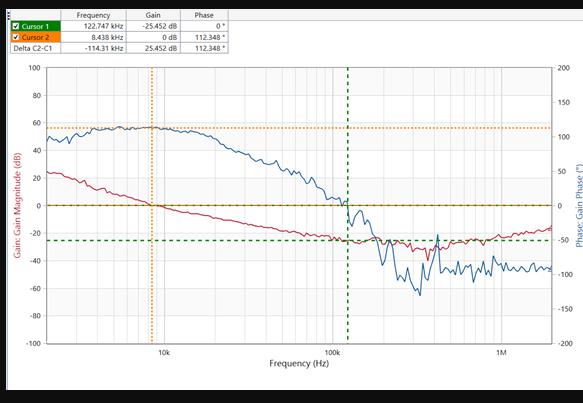
我們將該點叫做頻率轉折點,在頻率較低的范圍內,增益大約為1,在頻率較高的范圍內,系統增益以-20dB/10倍頻的速度下降。在濾波器設計中,也就是我們常聽到的3dB帶寬的截止頻率。低通濾波器的波特圖頻率響應部分如下所示:
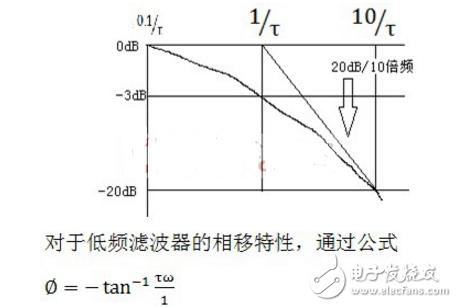
由于正切函數是非線性的,描述其特性比較難搞,其實我們可以依據我們擁有的基礎數學知識來近似描述該函數:

位為0°、45°和90°。在波特圖的相頻圖中畫出相應曲線,如下圖所示:
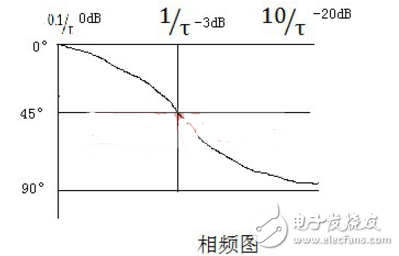
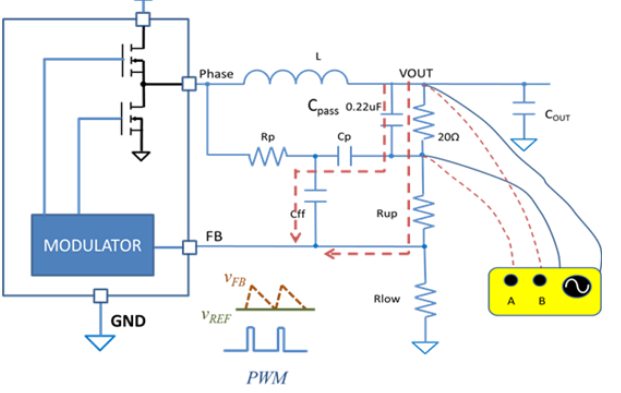
以上以一簡單的一階低通濾波器作為例子進行系統的波特圖分析和畫制,在實際的工程中,常常會因為采用多個電容和電阻構成了更加負責的系統,其實原理分析都是如此,只不過在分析過程中,找出關鍵位置的頻率點,就能掌握系統傳遞函數的綱要,達到高屋建瓴的效果。
在多極點和零點傳遞函數中,使分母為零的頻率點叫極點,使分子頻率為零的頻率點叫零點,極點可以使增益曲線下降,零點使增益曲線上升。在多極點和零點的系統中,只要找到各個極點和零點,找出其特性,將各個增益曲線疊加即可實現系統的極零分析,這個定理可以幫助大家在畫多極點和零點的傳遞函數有個直觀的印象。
 電子發燒友App
電子發燒友App










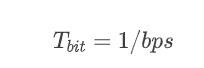
















評論