異或,是一個數學運算符,英文為exclusive OR,縮寫為xor,應用于邏輯運算。異或的數學符號為“⊕”,計算機符號為“xor”。其運算法則為:
a⊕b = (?a ∧ b) ∨ (a ∧?b)
如果a、b兩個值不相同,則異或結果為1。如果a、b兩個值相同,異或結果為0。
異或也叫半加運算,其運算法則相當于不帶進位的二進制加法:二進制下用1表示真,0表示假,則異或的運算法則為:0⊕0=0,1⊕0=1,0⊕1=1,1⊕1=0(同為0,異為1),這些法則與加法是相同的,只是不帶進位。
異或略稱為XOR、EOR、EX-OR
程序中有三種演算子:XOR、xor、⊕。
使用方法如下
z = x ⊕ y
z = x xor y
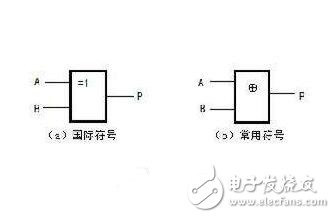
異或運算的作用
參與運算的兩個值,如果兩個相應bit位相同,則結果為0,否則為1。
即:
0^0 = 0,
1^0 = 1,
0^1 = 1,
1^1 = 0
按位異或的3個特點:
(1) 0^0=0,0^1=1 0異或任何數=任何數
(2) 1^0=1,1^1=0 1異或任何數-任何數取反
(3) 任何數異或自己=把自己置0
按位異或的幾個常見用途:
(1) 使某些特定的位翻轉
例如對數10100001的第2位和第3位翻轉,則可以將該數與00000110進行按位異或運算。
10100001^00000110 = 10100111
(2) 實現兩個值的交換,而不必使用臨時變量。
例如交換兩個整數a=10100001,b=00000110的值,可通過下列語句實現:
a = a^b; //a=10100111
b = b^a; //b=10100001
a = a^b; //a=00000110
(3) 在匯編語言中經常用于將變量置零:
xor a,a
(4) 快速判斷兩個值是否相等
舉例1: 判斷兩個整數a,b是否相等,則可通過下列語句實現:
return ((a ^ b) == 0)
舉例2: Linux中最初的ipv6_addr_equal()函數的實現如下:
static inline int ipv6_addr_equal(const struct in6_addr *a1, const struct in6_addr *a2)
{
return (a1-》s6_addr32[0] == a2-》s6_addr32[0] &&
a1-》s6_addr32[1] == a2-》s6_addr32[1] &&
a1-》s6_addr32[2] == a2-》s6_addr32[2] &&
a1-》s6_addr32[3] == a2-》s6_addr32[3]);
}
可以利用按位異或實現快速比較, 最新的實現已經修改為:
static inline int ipv6_addr_equal(const struct in6_addr *a1, const struct in6_addr *a2)
{
return (((a1-》s6_addr32[0] ^ a2-》s6_addr32[0]) |
(a1-》s6_addr32[1] ^ a2-》s6_addr32[1]) |
(a1-》s6_addr32[2] ^ a2-》s6_addr32[2]) |
(a1-》s6_addr32[3] ^ a2-》s6_addr32[3])) == 0);
}
5 應用通式:
對兩個表達式執(zhí)行按位異或。
result = expression1 ^ expression2
result
任何變量。
expression1
任何表達式。
expression2
任何表達式。
說明
^ 運算符查看兩個表達式的二進制表示法的值,并執(zhí)行按位異或。該操作的結果如下所示:
0101 (expression1)1100 (expression2)----1001 (結果)當且僅當只有一個表達式的某位上為 1 時,結果的該位才為 1。否則結果的該位為 0。
只能用于整數
下面這個程序用到了“按位異或”運算符:
class E
{ public static void main(String args[ ])
{
char a1=‘十’ , a2=‘點’ , a3=‘進’ , a4=‘攻’ ;
char secret=‘8’ ;
a1=(char) (a1^secret);
a2=(char) (a2^secret);
a3=(char) (a3^secret);
a4=(char) (a4^secret);
System.out.println(“密文:”+a1+a2+a3+a4);
a1=(char) (a1^secret);
a2=(char) (a2^secret);
a3=(char) (a3^secret);
a4=(char) (a4^secret);
System.out.println(“原文:”+a1+a2+a3+a4);
}
}
就是加密啊解密啊
char類型,也就是字符類型實際上就是整形,就是數字。
計算機里面所有的信息都是整數,所有的整數都可以表示成二進制的,實際上計算機只認識二進制的。
位運算就是二進制整數運算啦。
兩個數按位異或意思就是從個位開始,一位一位的比。
如果兩個數相應的位上一樣,結果就是0,不一樣就是1
所以111^101=010
那加密的過程就是逐個字符跟那個secret字符異或運算。
解密的過程就是密文再跟同一個字符異或運算
010^101=111
至于為什么密文再次異或就變原文了,這個稍微想下就知道了。。
異或運算:按位異或運算符
首先異或表示當兩個數的二進制表示,進行異或運算時,當前位的兩個二進制表示不同則為1相同則為0.該方法被廣泛推廣用來統(tǒng)計一個數的1的位數!
參與運算的兩個值,如果兩個相應bit位相同,則結果為0,否則為1。
即:
0^0 = 0,
1^0 = 1,
0^1 = 1,
1^1 = 0
按位異或的3個特點:
(1) 0^0=0,0^1=1 0異或任何數=任何數
(2) 1^0=1,1^1=0 1異或任何數-任何數取反
(3) 任何數異或自己=把自己置0
按位異或的幾個常見用途:
(1) 使某些特定的位翻轉
例如對數10100001的第2位和第3位翻轉,則可以將該數與00000110進行按位異或運算。
10100001^00000110 = 10100111
(2) 實現兩個值的交換,而不必使用臨時變量。
例如交換兩個整數a=10100001,b=00000110的值,可通過下列語句實現:
a = a^b; //a=10100111
b = b^a; //b=10100001
a = a^b; //a=00000110
位運算
位運算時把數字用二進制表示之后,對每一位上0或者1的運算。理解位運算的第一步是理解二進制。二進制是指數字的每一位都是0或者1.比如十進制的2轉化為二進制之后就是10。
其實二進制的運算并不是很難掌握,因為位運算總共只有5種運算:與、或、異或、左移、右移。如下表:

左移運算:
左移運算符m《《n表示吧m左移n位。左移n位的時候,最左邊的n位將被丟棄,同時在最右邊補上n個0.比如:
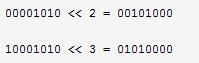
右移運算:
右移運算符m》》n表示把m右移n位。右移n位的時候,最右邊的n位將被丟棄。但右移時處理最左邊位的情形要稍微復雜一點。這里要特別注意,如果數字是一個無符號數值,則用0填補最左邊的n位。如果數字是一個有符號數值,則用數字的符號位填補最左邊的n位。也就是說如果數字原先是一個正數,則右移之后再最左邊補n個0;如果數字原先是負數,則右移之后在最左邊補n個1.下面是堆兩個8位有符號數作右移的例子:
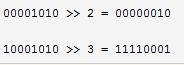
關于移位的運算有這樣的等價關系:把整數右移一位和把整數除以2在數學上是等價的。

計算機內部只識別1、0,十進制需變成二進制才能使用移位運算符《《,》》 。
int j = 8;
p = j 《《 1;
cout《《p《《endl;
在這里,8左移一位就是8*2的結果16 。
移位運算是最有效的計算乘/除乘法的運算之一。
按位與(&)其功能是參與運算的兩數各對應的二進制位相與。只有對應的兩個二進制位均為1時,結果位才為1,否則為0 。參與運算的數以補碼方式出現。
先舉一個例子如下:
題目:請實現一個函數,輸入一個正數,輸出該數二進制表示中1的個數。

這里用到了這樣一個知識點:把一個整數減去1,再和原整數做與運算,會把該整數最右邊一個1變成0 。 那么一個整數的二進制表示中有多少個1,就可以進行多少次這樣的操作。
總結:把一個整數減去1之后再和原來的整數做位與運算,得到的結果相當于是把整數的二進制表示中的最右邊一個1變成0 。
位運算的應用可以運用于很多場合:
清零特定位(mask中特定位置0,其它位為1 , s = s & mask)。
取某數中指定位(mask中特定位置,其它位為0, s = s & mask)。
舉例:輸入兩個整數m和n,計算需要改變m的二進制表示中的多少位才能得到n。
解決方法:第一步,求這兩個數的異或;第二步,統(tǒng)計異或結果中1的位數。
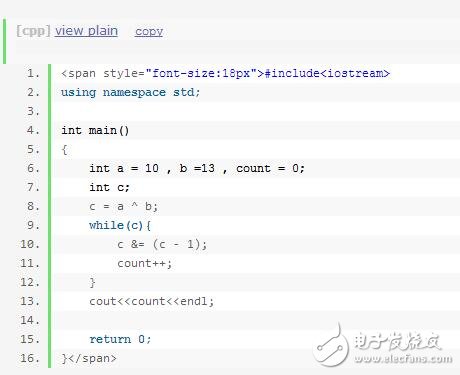
接下來我們再舉一例,就可以更好的說明移位運算了:用一條語句判斷一個整數是不是2的整數次方。
解決方法:一個整數如果是2的整數次方,那么它的二進制表示中有且只有一位是1,而其它所有位都是0 。 根據前面的分析,把這個整數減去1后再和它自己做與運算,這個整數中唯一的1就變成0了。
解答:!(x & (x - 1))
 電子發(fā)燒友App
電子發(fā)燒友App

























評論