1、引言
本課程設計主要用于MSK信號的調制與解調,同時進一步了解MSK信號的的解調調制原理以及其性能。再次基礎上進一步對信號疊加噪聲,并繪制相應波形,同時進行分析。
1.1課程設計目的
利用MATLAB集成環境下的M文件,編寫程序來實現MSK的調制解調,并繪制出解調前后的時域和頻域波形及疊加噪聲時解調前后的時頻波形,根據運行結果和波形來分析該解調過程的正確性及信道對信號傳輸的影響。通過這次課程設計進一步加深了我對最小二進制相移鍵控(MSK)調制解調性能的理解與掌握,同時將課堂上學到的理論知識用于實踐。增強了我在模擬仿真方面的能力,為以后系統開發和通信系統仿真打下了良好的基礎。
1.2課程設計要求
通過課程設計,掌握M文件的使用,同時進一步加深MSK調制解調的原理,在此基礎上編寫出MSK調制解調的程序。并繪制出MSK信號解調前后在時域和頻域中的波形,觀察解調前后頻譜有何變化以加深對MSK信號解調原理的理解。通過這一些之后再加上噪聲,對信號解調,并繪制出解調前后信號的時頻波形,改變噪聲功率進行解調,分析噪聲對信號傳輸造成的影響。
1.3課程設計步驟
先定義MSK輸入信號的參數然后用dmod函數做輸入的調制,之后畫相應的頻譜圖。再用dedmod做解調輸出。然后加入噪聲,再進行解調輸出。
1.定義載波頻率Fs,輸出信號頻率Fd,采樣頻率Fs。
2.設置輸入信號X,同時做信號的調制。
3.畫出相應的波形圖。
4.做輸出信號的解調波形,同時畫解調波形圖。
5.加入高斯白噪聲。再進行信號的解調輸出,畫相應的波形。
6.對結果進行比較分析。
1.4課程設計平臺
本課程設計中應用M文件設計MSK信號調制解調程序。所以在本課程設計中有必要對MATLAB進行簡要的描述。
MATLAB語言是當今國際上科學界最具影響力、也是最具活力的軟件。它具有強大的數學運算能力、方便實用的繪圖功能及語言的高度集成性。MATLAB是矩陣實驗室(MatrixLaboratory)之意。MATLAB除具備卓越的數值計算能力外,它還提供了專業水平的符號計算、文字處理、可視化建模仿真和實時控制等功能。
MATLAB的出現使得通信系統的仿真能夠用計算機模擬實現,免去構建實驗系統的不便,而且操作十分簡便,只需要輸入不同的參數就能得到不同情況下系統的性能,而且在結果的觀測和數據的存儲方面也比傳統的方式有很多優勢。因而MATLAB在通信仿真領域得到越來越多的應用。MATLAB的一大特點是提供了很多專用的工具箱和模塊庫,例如通信工具箱和模塊庫、數字信號處理工具箱和模塊庫、控制工具箱和模塊庫等,MATLAB在這些工具箱和模塊庫中提供了很多常用的函數和模塊,使得仿真更容易實現。
在本課程設計里,我們主要利用MATLAB中的M文件實現MSK解調器的設計,對解調前后波形進行比較,繪制時域波形。
2、MSK調制解調原理
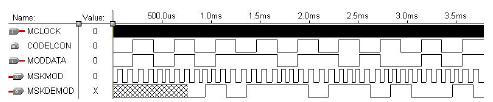
MSK信號是一種包絡恒定、相位連續、帶寬最小并且嚴格正交的2FSK信號,其波形如圖2-1所示。

2.1MSK基本原理
MSK信號是一種相位連續、包絡恒定并且占用帶寬最小的二進制正交FSK信號。它的第k個碼元可以表示為:

MSK信號具有特點如下:①MSK信號是正交信號;②其波形在碼元間是連續的;③其包絡是恒定不變的;④其附加相位在一個碼元持續時間內線性地變化2/??;⑤調制產生的頻率偏移等于T4/1?Hz;⑥在一個碼元持續時間內含有的載波周期數等于1/4的整數倍。
2.2MSK正交表示法
式(2-1)可以用頻率為sf的兩個正交分量表示。將式(2-1)進行三角公式變換,得到:
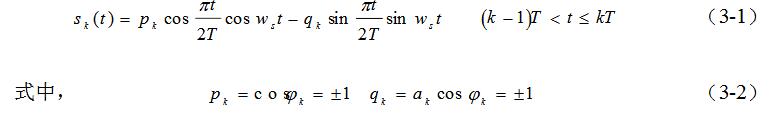
式(2-2)表示,此MSK信號可以分解為同相分量(I)和正交分量(Q)兩部分。
2.3MSK信號的調制
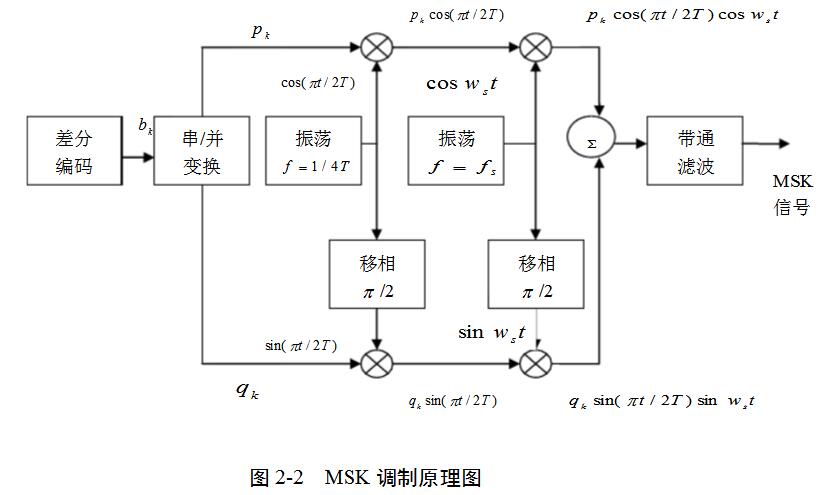
由式(2-2)可知,MSK信號可以用兩個正交的分量表示。根據該式構成的MSK信號的產生方框圖如圖2-2所示。
2.4MSK信號的解調
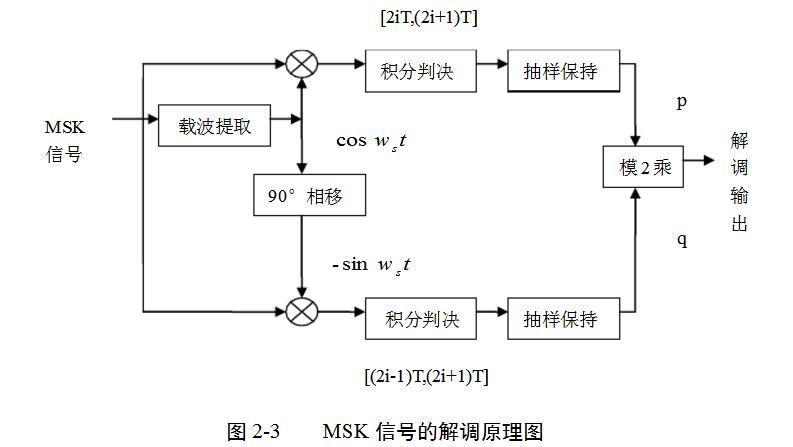
由于MSK信號是最小二進制FSK信號,所以它可以采用解調FSK信號的相干法和非相干法解調。
圖2-3是MSK信號的解調原理框圖。
3、仿真實現過程
3.1MSK信號的產生
因為MSK信號可以用兩個正交的分量表示:
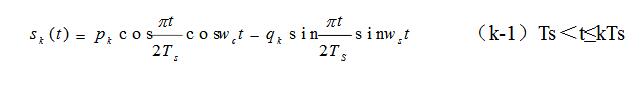
式中:右端第1項稱作同相分量,其載波為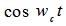 ;第2項稱作正交分量,其載波為
;第2項稱作正交分量,其載波為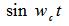 。
。
在仿真時先設置輸入信號的參數:載波頻率Fc調制后,數字信號速率Fd,模擬信號采樣率Fs。之后產生要調制的隨機數字信號x;然后用dmod函數進行調制,產生調制信號。dmod函數是MATLAB中一個常用來進行信號調制的函數,它后面的參數包括被調制信號,載波信號的頻率,輸出信號的速率以及采樣速率和所進行調制的函數。
部分程序代碼和仿真圖如下所示:
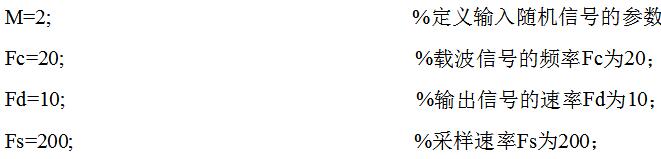
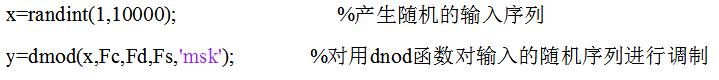
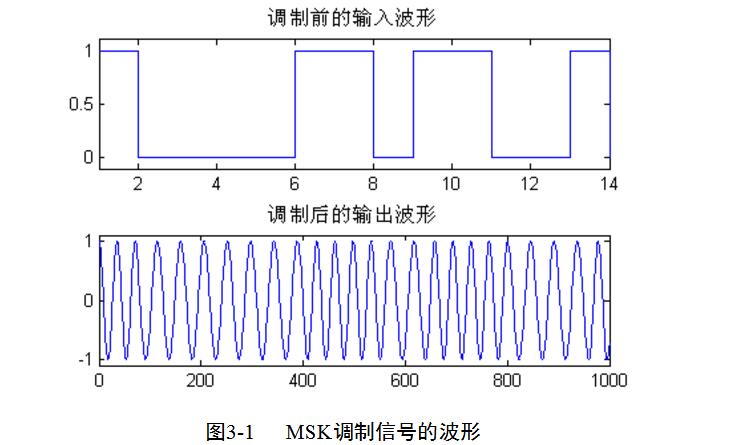
由調制波形圖可以看出MSK的調制信號特性與2FSK調制信號的特性非常的相似,即:當輸入信號為“1”時,調制后的波形比輸入信號為“0”時的波形要密。同時MSK信號的包絡是恒定的,相位則是連續的。帶寬相對于一般的2FSK信號要小,而且正交。
3.2MSK解調實現
由于MSK信號是最小二進制FSK信號,所以它可以采用解調FSK信號的相干法和非相干法解調。
在進行程序仿真時,用ddemod函數進行調制信號的解調。同時畫出解調前后的時域與頻域的波形圖。在畫頻域的波形圖時先對已調信號與解調信號進行DTFT變換,之后畫出相應的波形。ddemod函數是與dmod函數相對應,用來對已調信號進行解調的。其后面的參數與dmod函數后的一模一樣。
部分程序與仿真波形圖如下所示:
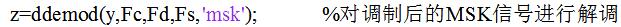
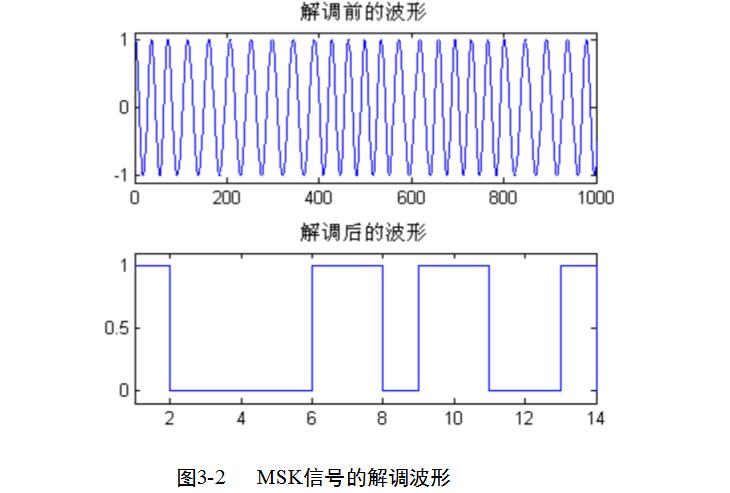
由解調信號的時域波形可以看出,解調后的波形與原始輸入信號的波形完全一致。同時不難發現解調后的信號很穩定。

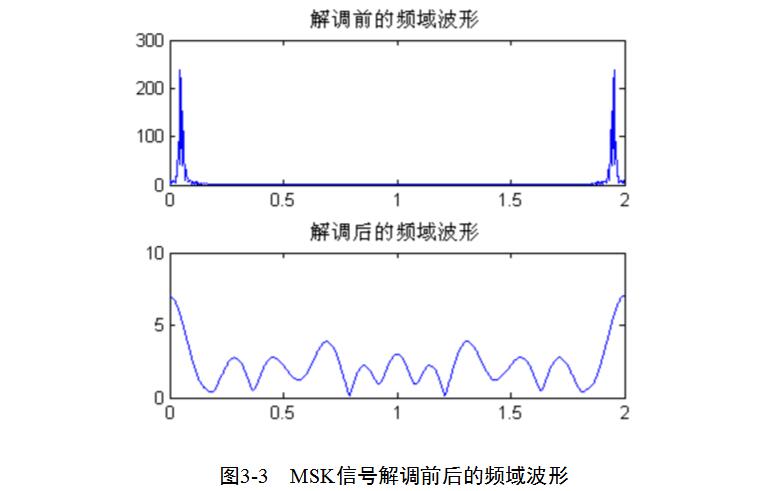
由解調后的頻域波形可以看出MSK信號的穩定性很好,說明MSK信號的抗噪聲性能很強。
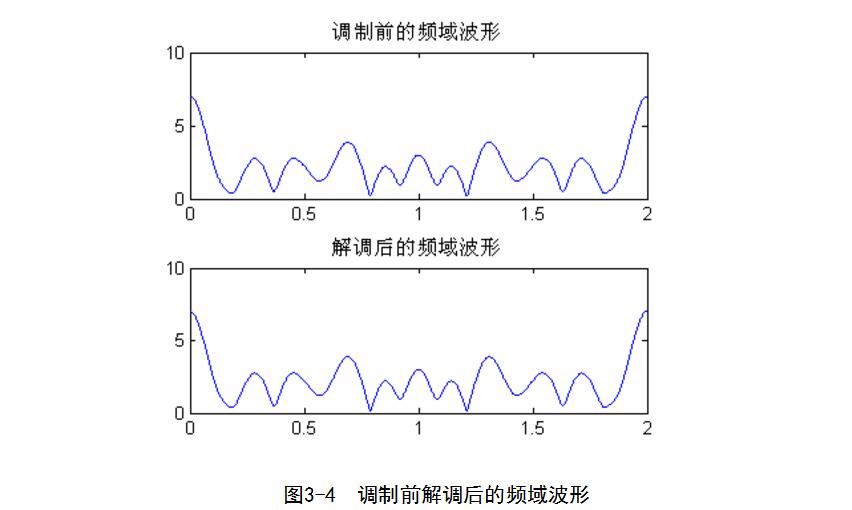
通過調制前和解調后的頻域波形比較,發現解調非常的成功,波形被完整無誤的輸出來。
3.3疊加噪聲的MSK解調
由于信號在傳輸的過程中難免要受到外來噪聲的影響,所以在進行通信仿真時務必要在理想的模擬通信系統中加入高斯白噪聲對系統進行影響,以此來判斷一個通信系統抗噪聲性能的好壞。
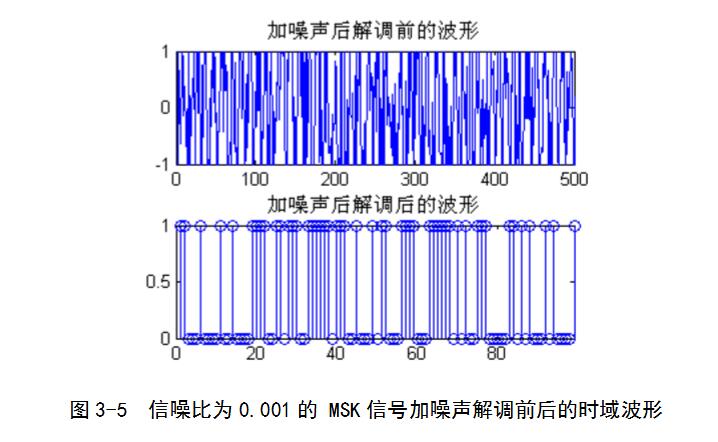
在這次課程設計中,我利用awagn函數對已調信號加入信噪比為0.001的高斯白噪聲。然后對加入了噪聲的已調信號進行解調,同時畫出其時域與頻域的波形,將其與沒有加噪聲的調制信號進行比較,不難發現:加入噪聲后對已調信號的影響很大,但對解調信號而言,噪聲對解調后的影響還是有一定限度的。這說明MSK解調系統的抗噪聲性能很強。
仿真的部分程序與相應的仿真波形圖如下所示:

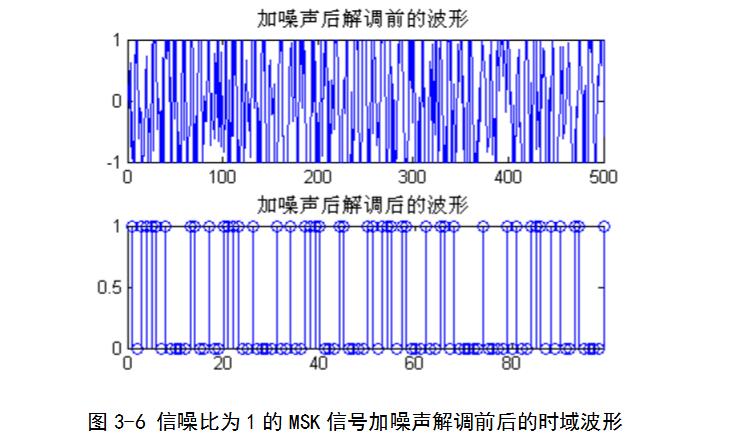
通過symerr函數對解調信號的誤碼率進行測定,得到的誤碼率為0.0024.因為輸入的隨機序列長度為10000,錯了24個。說明MSK信號的抗噪聲性能很強。當將信噪比變為1時,輸出的誤碼率很快發生了變化,由原來的0.0024變為了6.0000e-004.圖形也同時發生了變化。通過圖形的比較,可以發現噪聲對調制信號的影響很大,但通過解調后影響相對減小了很多。

在多次改變信噪比后,將信噪比與誤碼率聯合做了如圖3-8所式的波形圖。
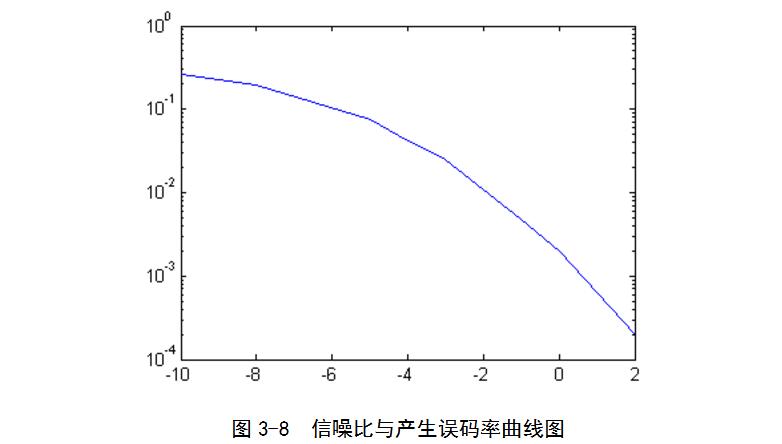
通過圖形可知,隨著系統信噪比的增加,解調后輸出的誤碼率隨之減小,當信噪比增加到一定程度時,誤碼率變為0。說明噪聲對信號的影響在一定程度上是可以減小,但很難消除,因為每一個系統都不可能是理想系統,總會受到外界的干擾。
4、遇到的問題及解決辦法
遇到的問題一:在設計程序時由于一開始使用的不是隨機序列,同時MSK信號的抗噪聲性能很強,當輸入的是有限個序列時,很難判斷出噪聲對信號的影響。所以在加入噪聲后再進行解調時根本就無法發現噪聲對信號的影響。
解決辦法:利用randint函數來產生100個隨機序列,然后再在調制好了的信號上加入高斯白噪聲,之后對調制信號解調。這樣發現噪聲對信號的一點點影響。遇到的問題二:在畫解調信號前后的頻域波形時,由于忽略了調制信號和解調后的信號長度不一致,所以只設置了一個參數n1,當進行仿真畫圖時一直都無法畫出來。解決辦法:在老師的指導下,我又重新檢查了一變程序。后來發現錯誤,并重新添加了參數n2,然后在進行DTFT轉換后畫圖得到了正確的結果。
遇到的問題三:在加入高斯白噪聲時,由于不清楚awgn這個函數,所以我一直按照參考書上的方法進行噪聲的添加,但噪聲卻一直沒有成功的添加。
解決辦法:在老師的知道下,我通過MATLAB里的help幫我很快了解了awgn函數,后來成功加入噪聲也是可想而知的了。
 電子發燒友App
電子發燒友App










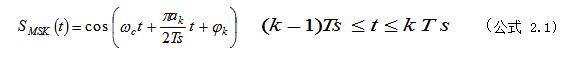
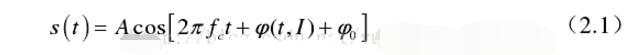











評論