空戰決策知識構建方法研究?
?本文來自《系統工程與電子技術》,作者呂躍等?
0 引言 隨著空戰訓練以及作戰仿真實驗的深入, 戰訓數據隨之大量產生, 需要解決“數據豐富, 知識貧乏”的數據應用問題, 挖掘數據背后的空戰決策知識, 客觀說明“人在回路”的空戰對抗過程。空戰決策知識是指在特定的空戰態勢情境下, 通過飛行員潛意識對態勢的理解和判斷, 做出相應機動決策積累的定性經驗知識。定性經驗知識蘊含在定量的戰訓大數據中, 如何通過技術手段分析、處理定量數據, 提取反應優秀飛行員空戰智慧經驗的戰術知識, 對于指導飛行員空戰決策以及多智能體智能化作戰具有重大意義。 空戰決策知識構建[1]是從外部空戰場態勢的顯性知識以及飛行員決策經驗型隱性知識轉換到計算機內部的過程, 包含態勢信息事實性知識和決策規則性知識。在知識表達方面, 文獻[2]提出了一種基于情境構建的經驗型隱性知識表示方法, 顯示飛行員空戰決策經驗知識用于無人戰斗機(unmanned combatair vehicle, UCAV)自主空戰決策; 文獻[3]基于謂詞演算, 提出飛行器能力的知識表示方法, 滿足飛行器自主決策的需求; 文獻[4]提出基于時序圖的作戰指揮行為知識表示學習方法, 有效地表征了具有時序關聯特征的作戰指揮行為。在空戰知識挖掘方面, 文獻[5]以飛行數據為研究對象, 提出改進人工免疫算法對飛行狀態規則進行提取, 驗證了規則在實際應用中的有效性; 文獻[6] 基于飛參特征變化和專家識別飛行動作的先驗知識建立了飛行動作識別知識庫, 可快速、準確識別各種機動動作。從研究現狀來看, 在知識表達方面, 對于戰場決策影響因素分析不夠全面, 并且未能描述空戰決策知識之間因果關系; 在知識挖掘方面, 對于直接從戰訓數據中獲取機動決策規則知識的研究較少, 且對于海量戰訓數據的挖掘利用不充分。 因此, 本文在戰訓數據的應用基礎上, 提出一種空戰決策知識構建方法, 對空戰決策知識的生成過程與表示方法進行分析與研究, 應用k-means聚類、最小描述長度準則(minimum description length principle, MDLP)數據預處理算法實現對戰訓數據的離群點檢測以及連續屬性離散化, 基于粗糙集理論和模糊邏輯推理實現空戰決策規則知識的挖掘與推理應用, 并將構建空戰決策知識應用于空戰對抗過程中, 以期解決“數據豐富、知識貧乏”的數據應用問題。 1 空戰決策知識 空戰決策知識是對當前對抗環境中空戰態勢和飛行員決策相互關系的抽象和描述, 它是建立在戰訓數據和飛行員經驗基礎上的知識處理, 是知識提取和知識理解的綜合過程, 滿足知識處理的“戰訓數據-特征信息-知識獲取-知識理解”層次結構。 1.1 空戰決策知識的生成 空戰決策知識生成環節可以分為空戰對抗過程信息特征提取、決策知識的生成、決策知識的展現3個部分, 如圖 1所示。空戰對抗過程信息特征提取包括對戰訓數據的預處理, 形成空戰態勢信息以及包含飛行員經驗的決策結果信息, 是知識生成環節的基礎; 決策知識的生成是知識生成環節的核心, 包括知識的提取、推理以及理解應用; 決策知識的展現表現為知識的可視化、互操作等, 是知識生成環節的后續階段[7]。
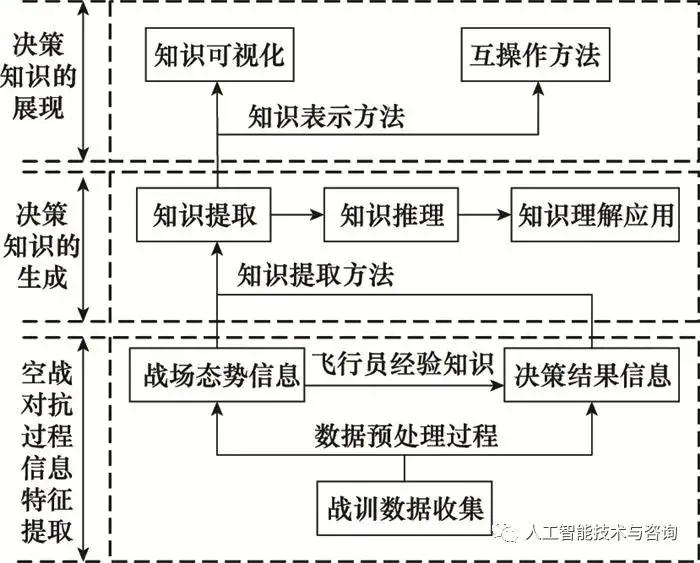
圖1 空戰決策知識生成過程 Fig.1 Air combat decision making knowledge generation process 本文將空戰決策知識分為戰場態勢信息事實性知識和飛行員決策規則性知識。戰場態勢信息事實知識是在戰訓數據的基礎上規范化描述戰場的態勢要素, 即空間幾何態勢、作戰能力、空情事件等及其關系的表達。空間幾何態勢和空情事件表示狀態信息的動態屬性知識, 作戰能力表示特征信息的靜態屬性知識[8]。可以表示為 == (1) 式中: Situation為空間幾何態勢的函數; Capability為相對作戰能力的函數; Incident表征空情事件的函數。 空間態勢幾何函數可以表示為 Situation (t)={TA(φ,q,t),Tv(vm,vt,t),Th(hm,ht,t),Td(D,DRmax,DMmax,DMkmin,DMkmax,t)} Situation (t)={TA(φ,q,t),Tv(vm,vt,t),Th(hm,ht,t),Td(D,DRmax,DMmax,DMkmin,DMkmax,t)} (2) 式中: φ、q為目標方位角、進入角; vm、vt為載機、敵機速度; hm、ht為載機、敵機高度; D為雙方作戰單元的距離; DRmax為雷達最大探測距離; DMmax為導彈最大攻擊距離; DMkmax、DMkmin為不可逃逸最大最小距離; TA、Tv、Th、Td為角度、速度、高度、距離態勢函數, 具體計算方式見參考文獻[8]。 相對作戰能力函數與敵我雙方戰機的總體作戰能力相關, 表示為 C=[lnB+ln(∑A1+1)+ln(∑A2)]ε1ε2ε3ε4C=[lnB+ln(∑A1+1)+ln(∑A2)]ε1ε2ε3ε4 (3) 式中: C為戰斗機總體作戰能力; B、A1、A2分別為戰斗機的機動能力參數、攻擊能力參數和探測能力參數; ε1、ε2、ε3、ε4分別為操縱能力參數、生存能力參數、航程能力參數和電子對抗能力參數[9]。作戰能力為靜態屬性知識, 通過戰場情報信息等手段獲取得到, 用離散值Capacity={-1, 0, 1}表征相對作戰能力的劣勢、均勢、優勢。 空情事件函數表示影響空戰勝負關鍵事件的關系, 表示為 Incident(t)={RaderOn(t),RaderLock(t), Weapon (t)}Incident(t)={RaderOn(t),RaderLock(t), Weapon (t)} (4) 式中:RaderOn(t)={0, 1}表示雷達開關機情況, 0表示雷達未開機, 1表示雷達已開機; RaderLock(t)={0, 1}表示雷達鎖定情況, 0表示雷達未鎖定, 1表示雷達已鎖定; Weapon(t)={0, 1}表示武器發射情況, 0表示導彈未發射, 1表示導彈已發射。 飛行員決策規則性知識是飛行員在當前態勢信息的基礎上, 根據作戰經驗以及個性化特征所做出的決策方案。 < Knowledge_of_Decision >=< Pilot (V), Action (Sa)>< Knowledge_of_Decision >=< Pilot (V), Action (Sa)> (5) 式中: Pilot(V)表示飛行員主觀風險態度形成的價值; Action(Sa)表示在飛行員在當前態勢下的空戰決策方案。 在激烈的空戰對抗環境下, 飛行員不能完全保持理性, 所以在面對風險和收益時存在不同的態度, 從而導致決策結果的不同, 這也屬于空戰決策知識組成部分。前景理論將人的心理偏好引入決策過程中, 并將心理偏好以風險態度系數、損失規避系數等形式量化[10], 能夠較好的描述飛行員空戰個性化特征知識。 Pilot(V)=∑i=0nπ(pi)v(Δxi)Pilot(V)=∑i=0nπ(pi)v(Δxi) (6) 式中: π(pi)為決策權重; v(Δxi)為價值函數; 具體形式為 v(Δx)={σ(Δx)α,Δx?0?δ(?Δx)β,Δx<0v(Δx)={σ(Δx)α,Δx?0?δ(?Δx)β,Δx<0 (7) 式中: Δx為結果相對于參考點的收益或者損失; α和β為飛行員的風險偏好及規避系數, 描述價值函數在收益區域及損失區域的凹凸程度; σ和δ為收益敏感系數和損失厭惡系數, 若飛行員對收益更加敏感, 則σ>δ≥1, 若飛行員對損失更加敏感, 則δ>σ≥1。 空戰決策方案集可以視為基本機動動作的組合, 當前態勢下的決策方案集可以表示為 Action(Sa)=[j1,j2,?,jk]Action(Sa)=[j1,j2,?,jk] (8) 式中:k=1, 2, …, 11, jk表示基于NASA學者提出的7種基本機動動作,改進得到完備的11種空戰機動動作[11], 決策問題可以表示為 ψΔt≤ts:{hm,h˙m,φ,φ˙,vm}→[j1,j2,?,jk]ψΔt≤ts:{hm,h˙m,φ,φ˙,vm}→[j1,j2,?,jk] (9) 式中:Δt為采樣時間; ts表示決策過程時間上限; φ表示航向角; ψ為機動動作特征參數到決策方案集的決策函數。 通過對上述機動動作集及戰斗機姿態的變化規律分析, 總結出各類機動動作對應上述特征參數的變化特征。將連續量機動特征參數區間化, 從而形成和定性描述的變化特征形成一一對應關系[12]。 在空戰的高對抗性下, 飛機機動是在極短時間內根據態勢情況調整機動動作特征屬性變化的過程。本文用區間數[t, t+Δt]描述特征屬性的變化范圍, 將機動動作集根據變化規律進行區間化, 將戰訓數據中機動動作特征指標值作為比較序列, 機動動作集中的區間基準特征值作為參考序列, 基于灰色關聯度模型, 求得關聯度大小來識別機動動作, 基于區間灰色關聯度機動動作識別模型實施步驟如下所示。 步驟 1 將機動動作基準特征參數區間化 u~ij=[uij???,uijˉˉˉˉˉˉ]=[xij?2σij,xij+2σij]u~ij=[uij_,uijˉ]=[xij?2σij,xij+2σij] (10) 式中:u~u~ij表示第i種基準機動動作的第j種特征指標值區間數; xij表示第i種基準機動動作的第j種特征指標值; σij表示標準方差。 步驟 2 構建決策矩陣Uˉ=[uijˉˉˉˉˉˉ]11×5Uˉ=[uijˉ]11×5并進行規范化處理, 得到新矩陣V~=[v~ij]11×5V~=[v~ij]11×5, 規范化方法見參考文獻[8]。 步驟 3 計算比較序列與參考序列之間的關聯系數ξi(k) ξi(k)=minimink(D0i)+ρmaximaxk(D0i)D0i+ρmaximaxk(D0i)ξi(k)=minimink(D0i)+ρmaximaxk(D0i)D0i+ρmaximaxk(D0i) (11) 式中:ρ為分辨系數; D0i為比較序列與參考序列區間數的歐式距離。 步驟 4 計算待識別機動動作與基本動作集的關聯度Zi, 比較關聯度大小識別機動動作。 Zi=1n∑k=1nξi(k),k=1,2,?,nZi=1n∑k=1nξi(k),k=1,2,?,n (12) 1.2 空戰決策知識的表示 空戰決策知識是態勢屬性結合飛行員特征到機動動作的映射, 既包含事實性知識又包含規則性知識, 存在知識間的因果關系。產生式規則表示法用于表示知識之間的因果關系, 與人的判斷性知識基本一致, 且可以提供高粒度信息, 容易描述事實、規則以及它們的數量測度[13], 適用于空戰決策知識的表示。 1.2.1 戰場態勢信息事實性知識的表示 產生式表示方法一般采用3元組對象、屬性、值或者3元組關系、對象1、對象2來表示戰場態勢信息事實。若考慮態勢信息獲取的不確定性, 可以加入可信度量用4元組對象、屬性、值、可信度來表示。例如: (敵機, 角度威脅值, 0.5)(態勢, 載機, 敵機)(空情事件, 武器發射, 1, 0.8)。 1.2.2 飛行員決策規則知識的表示 飛行員決策規則知識是指在空戰問題中的因果關系的知識, 可表示為 if Condition then Action(Sa) if Condition then Action(Sa) (13) 式中: condition為規則前件, 是戰場態勢信息以及飛行員個性化特征的合取, 表示為 Condition =( Situation ∧ Capability ∧ Incident ∧Pilot(V)) Condition =( Situation ∧ Capability ∧ Incident ∧Pilot(V)) (14) 式中:Action(Sa)為規則后件, 是基于規則前件的決策方案。 2 戰訓數據預處理 在戰訓數據收集、存儲過程中,如果受到外界環境的干擾, 所記錄的戰訓數據將會包含隨機干擾和誤差, 數據中存在離群點, 導致數據質量難以滿足空戰知識挖掘的要求。其次, 戰訓數據采用連續值記錄的方式難以滿足算法離散度量屬性的要求。基于此, 本節采用基于k-means聚類的離群點檢測以及基于MDLP的連續屬性離散化來處理原始戰訓數據, 解決低質量戰訓數據導致的知識挖掘算法執行效率低以及知識生成偏差的問題。 2.1 基于k-means聚類的離群點檢測 基于k-means聚類的離群點檢測是通過聚類分析發現與其他對象無強相關的對象, 如果一個對象不強屬于任何簇, 則認為該對象屬于聚類的離群點[14]。戰訓數據集D被k-means聚類算法分為k個簇, C={C1, C2, …, Ck}, 對象p與所有簇間距離間的加權平均值為離群因子OF(p)。 OF(p)=∑i=1k|Cj||D|?d(p,Cj)OF(p)=∑i=1k|Cj||D|?d(p,Cj) (15) 基于k-means聚類的離群點檢測流程如表 1所示。 表1 離群點檢測流程 Table 1 Process of outlier detection(t),capability,incident(t)>(t),capability,incident(t)>
| 輸入 戰訓數據集D; 聚類個數k; |
新窗口打開| 下載CSV 基于k-means聚類的離群點檢測的時間和空間復雜度是線性或者接近于線性的, 效率較高, 適用于大規模數據集。 2.2 基于MDLP的連續屬性離散化 屬性值離散化是進行數據壓縮、提取決策規則的基礎, 有效的屬性離散化算法不僅可以提高知識挖掘的效率, 并且可以從得到的離散戰訓數據中獲取相對簡潔的空戰決策知識規則。 MDLP是一種具備監督連續屬性離散化的技術, 在選擇最佳的切分點時, 考慮決策信息對屬性進行遞歸分割的影響[15], 其消息編碼的位數l為 l=Ent(O)=?∑i=1kpilog2pil=Ent(O)=?∑i=1kpilog2pi (16) 式中: 編碼位數l對應了分類的熵Ent(O); k對應連續屬性論域O={O1, O2, …, Ok}被決策屬性A∈D分割后子集的個數。 條件屬性B∈C將O′∈O分為若干子集O′={O′1, O′2, …, O′m}, 則條件屬性B對O分類后的熵為 Ent(B,O)=∑i=1mpiEnt(Oi)Ent(B,O)=∑i=1mpiEnt(Oi) (17) 式中: pi為權重, 即Oi的元素占論域O的比例。 pi=|Oi||O|,i=1,2?,mpi=|Oi||O|,i=1,2?,m (18) 條件屬性B會影響信息熵的壓縮, 信息增益為 Gain(B)=Ent(O)?Ent(B,O)Gain(B)=Ent(O)?Ent(B,O) (19) 基于MDLP的連續屬性離散化方法實施步驟為: 首先確定所有的候選離散切分點集dj(j=1, 2, …, k), 在確定候選集時不需要在所有屬性值中間確定切分點, 只需將屬性值排序后選取類別不同的兩點值間作為候選切分點。其次, 搜尋點df將論域O劃分為O=O1∪O2兩部分, 并且滿足以下條件: Gain(df)>log2(n?1)n+δ(df)nGain(df)>log2(n?1)n+δ(df)n (20) 式中: δ(df)=log2(3t?2)?tEnt(O)+∑i=12tiEnt(Oi)δ(df)=log2(3t?2)?tEnt(O)+∑i=12tiEnt(Oi) (21) 式中: n=|O|為戰訓數據樣本數; t為論域O中包含的類別數。 最后, 將上述O1、O2兩子區間重復遞歸上述步驟, 直至式(20)不滿足為止。 3 基于粗糙集模糊理論的空戰決策知識推理 粗糙集(rough set, RS)理論能夠有效地處理戰訓數據, 從中發現隱含的空戰決策知識, 通過決策知識屬性的約簡, 提取飛行員空戰最小決策規則知識。模糊邏輯(fuzzy logical, FL)推理能夠將戰場態勢信息和飛行員個性化特征, 根據粗糙集提取的最小決策規則推理得到模糊邏輯決策即機動動作的控制量, 實現空戰決策知識的推理與應用。 3.1 基于RS最小空戰決策規則知識庫 S=(U, A, V, f)[16]是空戰決策知識信息表, 其中: U={x1, x2, …, xm}為戰訓數據集; A=C∪D={a1, a2, …, an}為屬性集合; 子集C為條件屬性, 代表戰場態勢信息及飛行員個性化特征; 子集D為決策屬性, 代表機動動作方案集; V=?a∈AVaV=?a∈AVa為屬性值的集合, f: U×A→V為U和A之間的關系集。 屬性子集a在U上不可分辨關系Ia為 Ia={(x,y)∈U×U:f(x,a)=f(y,a),?a∈A}Ia={(x,y)∈U×U:f(x,a)=f(y,a),?a∈A} (22) 在S中屬性a的決策矩陣[17]為 MDa(S)=(δDa(xi,xj))m×mMaD(S)=(δaD(xi,xj))m×m (23) 式中: δDa(xi,xj)={a∈A:a(xi)≠a(xj) 且 ?A(xi)≠?A(xj)}δaD(xi,xj)={a∈A:a(xi)≠a(xj) 且 ?A(xi)≠?A(xj)} (24) 通過決策矩陣ΜαD建立x∈U的決策函數為 fDA(x)=?y∈U{∨a?:a∈δDA(x,y) 且 δDA(x,y)≠?}fAD(x)=?y∈U{∨a?:a∈δAD(x,y) 且 δAD(x,y)≠?} (25) 對信息表S中所有決策類進行區分: gDA(U)=?x∈UfDA(x)gAD(U)=?x∈UfAD(x) (26) 式中: gAD(U)的主蘊涵表示區分決策類所需條件屬性最小子集。 決策表中決策屬性D的約簡滿足下述關系: B∈Red(S, D)?∧a∈Ba?∧a∈Ba?為gAD(U)的一個主蘊涵; B∈Red(S, x, D)?∧a∈Ba?∧a∈Ba?為fAD(x)的一個主蘊涵。 由約簡確定最小決策規則: RUL(S,x,d)={FB(x)→(?B=?B(x)):B∈Red(S,x,d)}RUL(S,x,d)={FB(x)→(?B=?B(x)):B∈Red(S,x,d)} (27) RUL(S,d)=?x∈URUL(S,x,d)RUL(S,d)=?x∈URUL(S,x,d) (28) 3.2 空戰決策規則知識模糊邏輯推理 模糊邏輯推理是基于模糊邏輯中的蘊涵關系和推理規則來進行[18], 是模糊邏輯控制的基礎, 是進行不確定性推理的方法之一, 空戰決策規則知識模糊邏輯推理系統組成如圖 2所示。
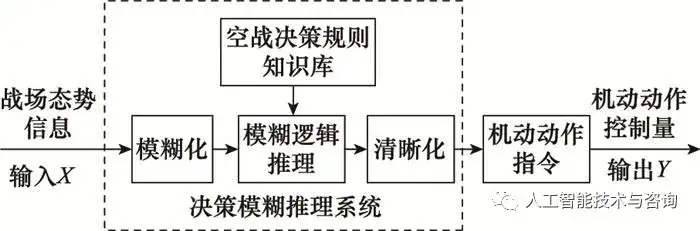
圖2 模糊邏輯推理系統組成 Fig.2 Composition of fuzzy logic inference system 決策模糊推理系統的輸入X與輸出Y分別為戰場態勢信息以及飛行員個性化特征知識X={Situation, Capacity, Incident, Pilot}和機動動作控制量切向過載、法向過載以及滾轉角Y={nx, nz, γ}, 其數學表現形式為 X(x1,x2,x3,x4)?FLJ(j1,j2,?,j11)?MPY={nx,ny,γ}X(x1,x2,x3,x4)?FLJ(j1,j2,?,j11)?MPY={nx,ny,γ} (29) 式中: FL表示模糊推理過程; J為11中機動動作方案集; MP機動動作與控制量之間的對應關系。 空戰決策規則知識庫由粗糙集理論進過屬性約簡后確定的最小決策規則得到, 用“if…then…”語句表示, 其規則庫形式為 R={R1MISO,R2MISO,?,RnMISO}R={RMISO1,RMISO2,?,RMISOn} (30) 式中: RMISO表示多輸入單輸出規則。 RiMISO={[(A1×A2×?×An)→Di1],[(A1×A2×?×An)→Di2],?,[(A1×A2×?×An)→Diq]}RMISOi={[(A1×A2×?×An)→Di1],[(A1×A2×?×An)→Di2],?,[(A1×A2×?×An)→Diq]} (31) 對于第i條規則的模糊蘊涵關系Ri定義為 Ri=(A1 and A2 and ? and Ai)→DiRi=(A1 and A2 and ? and Ai)→Di (32) 即: uRi=u(A1 and A2 and ? and Ai)→Di(a1,a2,?,ai,di)=[uA1(a1) and uA2(a2) and ? and uAi(ai)]→uDi(di)uRi=u(A1 and A2 and ? and Ai)→Di(a1,a2,?,ai,di)=[uA1(a1) and uA2(a2) and ? and uAi(ai)]→uDi(di) (33) 式中: u為模糊隸屬度函數。 3.3 空戰決策知識構建流程 將粗糙集理論和模糊邏輯推理理論相結合構成了空戰決策知識的構建模型, 其基礎是戰訓數據以及戰訓數據的預處理, 具體流程如圖 3所示。
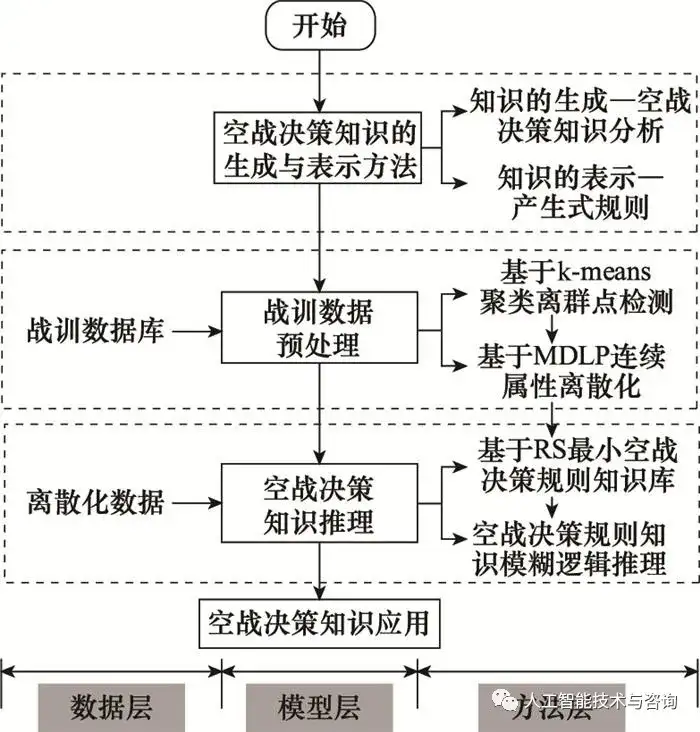
圖3 空戰決策知識構建流程 Fig.3 Construction process of Air combat decision knowledge 4 仿真分析與驗證 4.1 戰訓數據預處理 選取部分飛行速度數據為例, 并檢驗算法的有效性, 設置參數k=2, 閾值Θ=1 500。待檢測速度樣本以及離群點檢測如圖 4所示。
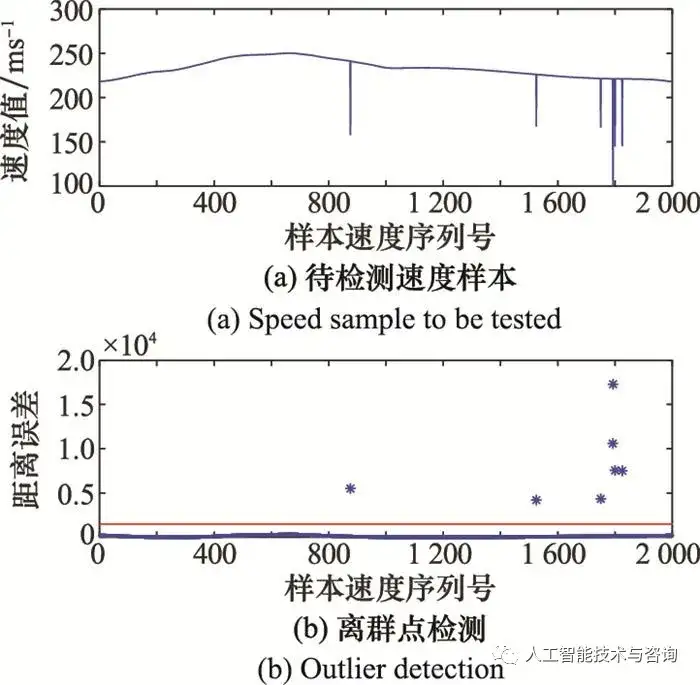
圖4 原始數據離群點檢測 Fig.4 Original data outlier detection 從圖 4檢測結果來看, 待檢測速度樣本中存在離群點, 序列號為(876, 1 525, 1 750, 1 792, 1 793, 1 800, 1 825), 表明本文采用的數據離群點檢測方法是有效的。 將機動動作識別結果作為決策屬性, 根據戰訓數據中角度、速度、距離和高度數據, 以及文獻[8]提出的態勢優勢函數, 計算得到戰場態勢信息事實性知識中的空間幾何態勢為連續屬性值, 部分節點態勢值如圖 5所示, 基于MDLP連續屬性離散化方法得到離散型知識, 如圖 6所示。
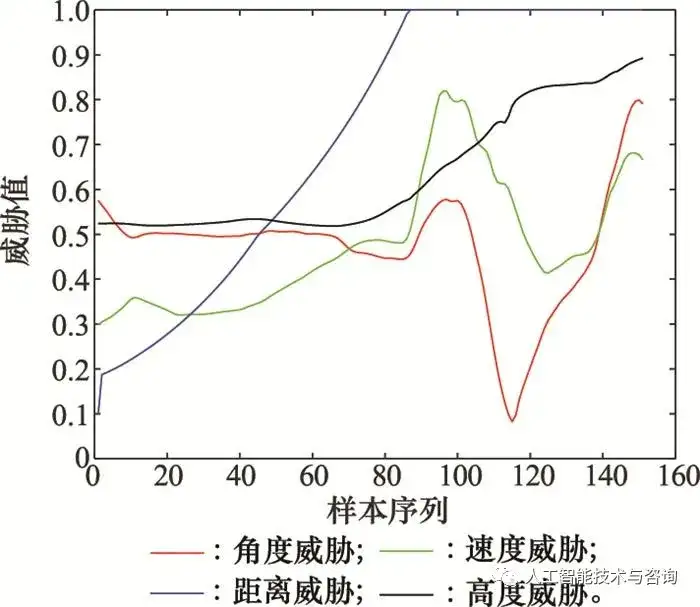
圖5 空戰幾何態勢圖 Fig.5 Geometry of air combat
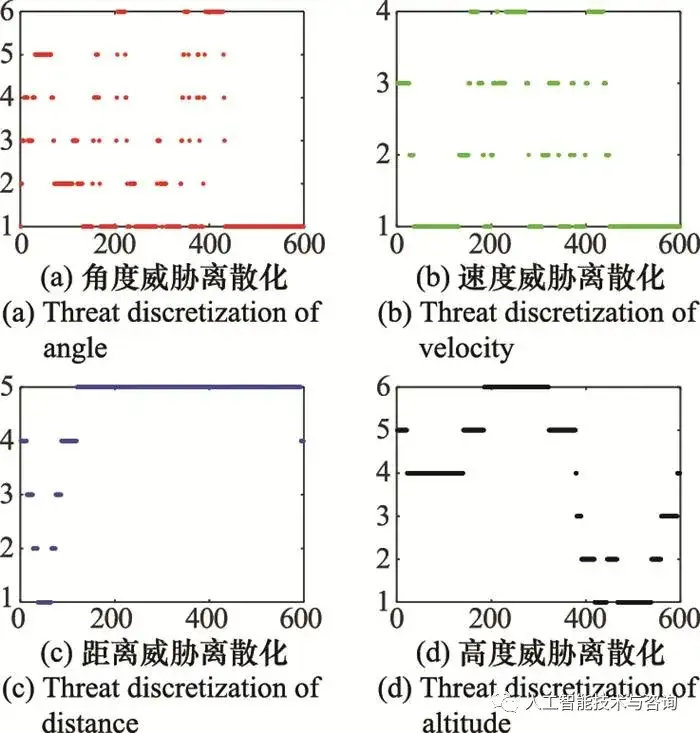
圖6 離散化空戰幾何態勢知識 Fig.6 Discretization of geometric situation knowledge of air combat 從圖 5空戰幾何態勢圖來看, 空戰對抗過程是高對抗性以及高敏捷性的敵我雙方博弈過程, 飛行員根據作戰經驗以及對空戰事實性知識的理解, 做出相應的機動動作, 這其中包含了豐富的空戰決策知識, 從中提取有效的決策規則知識對于指導飛行員作戰以及空戰智能決策具有重要意義。 從圖 6離散化結果來看, MDLP方法分別選取了角度威脅、速度威脅、距離威脅和高度威脅連續屬性的5個、3個、4個、5個切分點, 并將其分為[1,6]、[1,4]、[1,5]、[1,6]離散值區間, 滿足式(20)條件, 切分點如表 2所示。 表2 切分點區間 Table 2 Segmentation points interval
| 威脅屬性 | 切分點區間 |
新窗口打開| 下載CSV 4.2 機動動作識別 選取時間間隔Δt=0.5 s, 分辨系數ρ=0.5, 用區間數表示戰訓數據中記錄的我方機動動作特征參數值, 每種機動動作的識別用5種特征參數計算, 即高度hm、高度變化率h˙h˙m、航向角φ、航向角變化率φ˙φ˙、速度vm。根據專家知識將機動動作集J=[j1, j2, …, jk], k=1, 2, …, 11依次分為勻速直飛、加速前飛、減速前飛、爬升、左爬升、右爬升、俯沖、左俯沖、右俯沖、左轉彎、右轉彎11種, 各機動動作參數特征分析如表 3所示。 表3 機動動作特征參數分析 Table 3 Analysis of characteristic parameters of maneuver
| J | hm | h˙h˙m | φ | φ˙φ˙ | vm |
新窗口打開| 下載CSV 根據式(10)得到的計算機動動作特征參數方差σij, 得到基準特征參數區間數u~u~ij, 構建決策矩陣并規范化處理得到新矩陣V~V~, 將待識別機動動作的特征參數值作為行向量, 規范化處理后計算與參考序列之間的距離D0i, 根據式(11)計算比較序列與參考序列之間的關聯系數ξi(k), 根據式(12)計算關聯度大小Zi, 比較關聯度大小識別機動動作, 基于區間關聯度的機動動作識別結果如圖 7所示。

圖7 機動動作識別 Fig.7 Maneuvering identification 4.3 空戰最小決策規則提取 在空戰對抗前, 根據戰場情報信息等手段判斷敵機類型, 根據式(3)計算得到敵我雙方相對作戰能力; 在戰訓大數據中包含了雷達的開關機時間、雷達狀態、武器狀態等信號參數, 通過對數據的分析、提取, 得到空情事件的狀態, 形成空情事件知識; 在高對抗性和敏捷性的空戰環境下, 飛行員面對態勢風險和收益時, 根據飛行員主觀特點以及經驗, 會有保守型, 穩健型和冒險型的不同決策態度, 這也是空戰決策知識的組成部分之一, 根據式(6)~式(7)和文獻[10]方法計算得到不同飛行員在面對不同態勢下的價值, 離散化形成飛行員個性化特征知識。為了表示方便將角度威脅、速度威脅、距離威脅、高度威脅、相對作戰能力、雷達開關機、雷達鎖定、武器發射、飛行員個性化特征9個空戰決策條件屬性記為a1, a2, a3, a4, a5, a6, a7, a8, a9, 空戰機動動作決策屬性記為D, 由于篇幅限制, 列出部分節點空戰知識構建決策信息表如表 4所示。 表4 決策信息表 Table 4 Decision information table
| 戰訓數據集U | 決策屬性D | 條件屬性C | ? | ? | ? | ? | ? | ? |
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 |
新窗口打開| 下載CSV 通過式(22)~式(24)構建對稱的決策矩陣MaD(S)600×600, 由于決策信息表中存在不相容的數據, 說明針對不同的態勢知識情況, 飛行員做出的決策存在不確定性, 本文暫不考慮, 將不相容數據刪除處理。決策表全局約簡為 gDA(U)=?x∈UfDA(x)=(a1∧a2∧a3∧a4∧a9)∨(a1∧a2∧a3∧a4∧a8)gAD(U)=?x∈UfAD(x)=(a1∧a2∧a3∧a4∧a9)∨(a1∧a2∧a3∧a4∧a8) 空戰知識全局決策具有下列主蘊涵: (a1∧a2∧a3∧a4∧a9),(a1∧a2∧a3∧a4∧a8)(a1∧a2∧a3∧a4∧a9),(a1∧a2∧a3∧a4∧a8) 這些主蘊涵可以導出屬性約簡: {a5,a6,a7,a8},{a5,a6,a7,a9}{a5,a6,a7,a8},{a5,a6,a7,a9} 通過空戰決策信息表的約簡得到區分決策屬性所需最小條件屬性集合, 對應著空戰最小決策規則知識, 計算共得到83條規則, 圖 8為基于平行坐標圖的部分規則可視化。

圖8 空戰決策規則可視化 Fig.8 Visualization of air combat decision rules 4.4 構建空戰決策規則知識模糊邏輯推理系統 進行空戰決策知識推理之前需要將態勢信息等清晰量模糊化, 將觀測量映射為模糊集合。根據基于MDLP劃分的切分點區間設計模糊隸屬度函數能夠有效地決策屬性對屬性遞歸分割的影響。選擇高斯型隸屬函數, 能夠體現人類判斷的思維方式。 高斯函數的中心點c為鄰近區分點的中心點, 曲線的寬度根據區分點區間長度來設定, 圖 9為角度威脅模糊隸屬度函數, 圖 10為模糊規則瀏覽器。
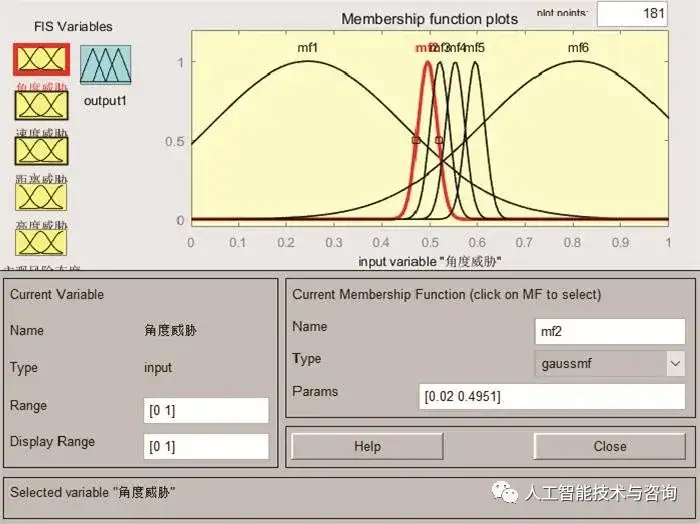
圖9 角度威脅模糊隸屬度函數 Fig.9 Angle threat fuzzy membership function
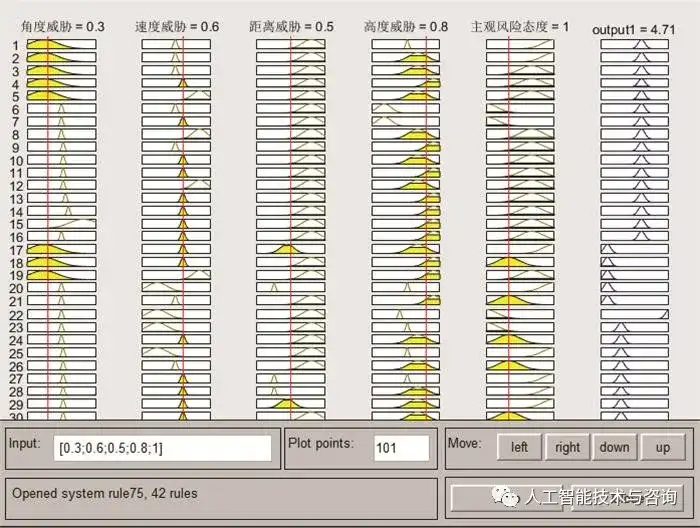
圖10 模糊規則瀏覽器 Fig.10 Fuzzy rules browser 4.5 空戰決策知識應用 將構建的空戰決策規則知識模糊推理系統應用到空戰對抗過程中, 驗證方法的有效性。 情況 1 目標作左轉彎機動, 初始時刻載機尾后接敵 載機的初始位置為(0, 0, 5 000)m, 速度為350 m/s, 航跡傾角為0°, 航跡偏角為-120°, 目標的初始位置為(30 000, 30 000, 5 000)m, 速度為350 m/s, 航跡傾角為0°, 航跡偏角為-120°, 空戰對抗軌跡如圖 11所示, 載機機動決策指令如圖 12所示, 基于參考文獻[8]中態勢評估模型計算出的態勢變化情況如圖 13所示。
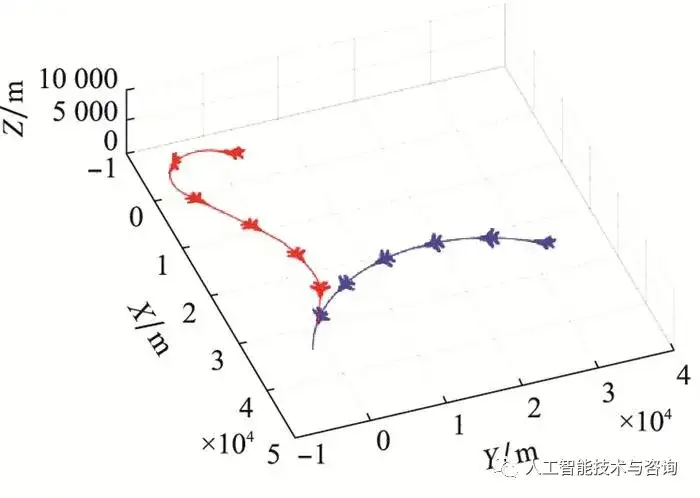
圖11 空戰對抗軌跡 Fig.11 Air combat trajectory
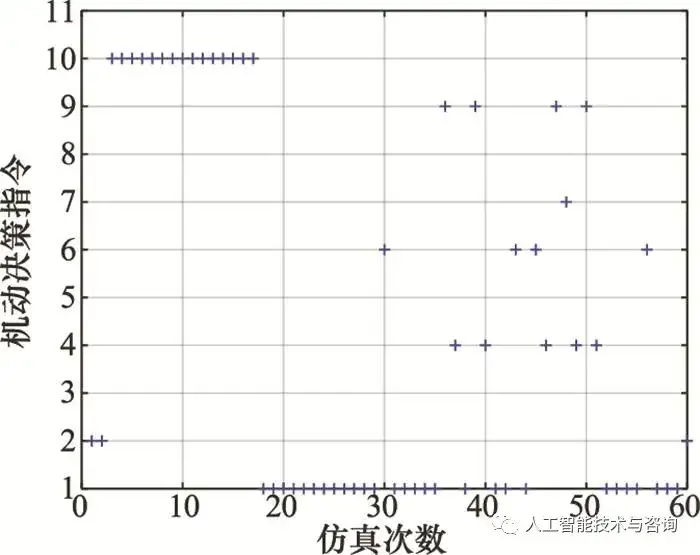
圖12 情況1時載機機動決策指令 Fig.12 Our fighter's maneuver decision instruction in case 1
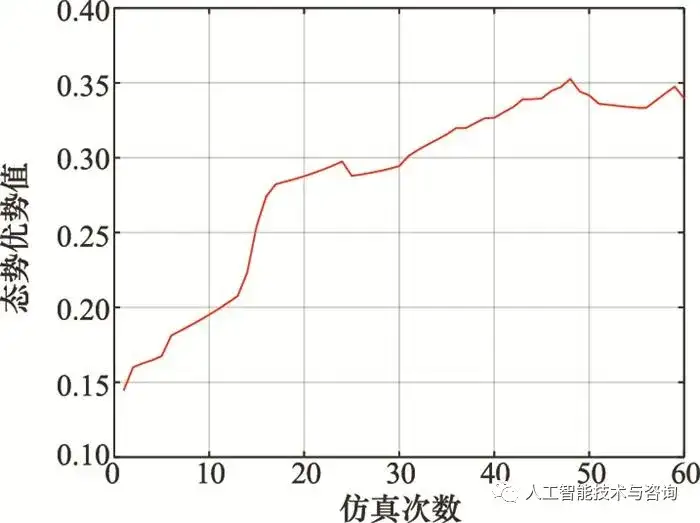
圖13 情況1時載機相對態勢優勢 Fig.13 Relative situation advantage of our fighter in case 1 從圖 10~圖 13可以看出, 當目標處于載機側后方時, 載機處于態勢劣勢, 載機進行加速前飛以及左轉彎機動正向接敵, 并且結合進行右爬升、爬升以及右俯沖占據最佳高度, 繞至目標后方并形成對目標的尾追態勢, 獲取態勢相對優勢。 情況 2 目標作蛇形機動, 初始時刻載機正面接敵 載機的初始位置為(0, 0, 5 000)m, 速度為350 m/s, 航跡傾角為0°, 航跡偏角為60°, 目標的初始位置為(30 000, 30 000, 5 000)m, 速度為350 m/s, 航跡傾角為0°, 航跡偏角為-90°, 空戰對抗軌跡、載機機動決策指令以及態勢變化情況如圖 14~圖 16所示。

圖14 空戰對抗軌跡 Fig.14 Air combat trajectory
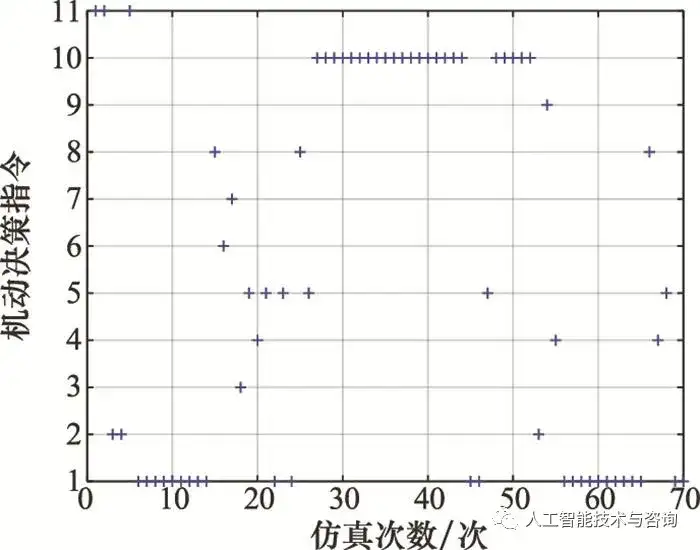
圖15 情況2時載機機動決策指令 Fig.15 Our fighter's maneuver decision instruction in case 2
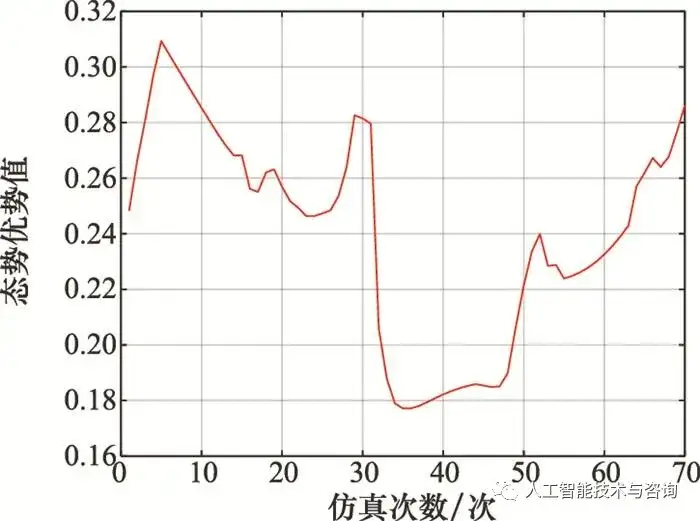
圖16 情況2時載機相對態勢優勢 Fig.16 Relative situation advantage of our fighter in case 2 從圖 14~圖 16可以看出, 初始階段載機與目標處于迎頭態勢, 載機與目標均可采用側向迂回接敵的策略, 載機加速前飛以及右轉彎機動, 隨著空戰距離的縮進, 載機的相對態勢優勢值逐漸減小, 在迎頭階段未分出勝負情況下, 載機與目標都會進行轉彎機動, 目的是繞至對方后方形成尾追態勢, 載機采用大過載機動, 連續左轉彎, 迅速繞至目標后方形成尾追態勢, 重新獲取空戰態勢相對優勢。 本文構建的空戰決策知識屬于單步決策, 是根據當前戰場態勢事實性知識在飛行員主觀因素影響下得出的單步決策方案, 提取的空戰決策規則知識是基于1Vs1空戰仿真案例, 適用于1Vs1條件下飛行員當前時刻機動動作決策提示或者1Vs1條件下自主空戰機動動作選擇。 5 結論 本文從空戰決策知識的生成與表示出發, 在全面考慮空戰場決策影響因素基礎上, 研究了空戰決策知識的生成與表示方法; 由于戰訓數據存在噪聲數據以及連續屬性數據難以滿足數據挖掘算法離散度量的要求, 應用了數據離群點檢測以及連續屬性離散化算法, 均能達到較好的數據預處理效果; 基于預處理后的戰訓數據, 提出了一種空戰最小決策規則提取方法以及空戰決策知識的應用推理方法。通過仿真驗證分析, 本文提出的空戰決策知識構建方法能夠應用在指導飛行員1Vs1空戰決策以及1Vs1無人作戰方面, 對于解決戰訓大數據處理與應用、空戰知識挖掘問題具有借鑒意義, 后續將進一步研究空戰決策規則知識的精度與適用度問題以及多機協同下空戰決策知識的構建問題。
審核編輯:符乾江 電子發燒友App
電子發燒友App
















































評論