在當今世界中許多重要的數據集都以圖或網絡的形式出現:社交網絡、知識圖表、蛋白質交互網絡、萬維網等。然而直到最近,人們才開始關注將神經網絡模型泛化以處理這種結構化數據集的可能性。
目前其中有一些在專業領域中都得到了非常好的結果,在這之前的最佳結果都是由基于核的方法、基于圖論的正則化方法或是其他方法得到的。
大綱
神經網絡圖模型的簡要介紹
譜圖卷積和圖卷積網絡(GCNs)
演示:用一個簡單的一階 GCN 模型進行圖嵌入
將 GCNs 視為 Weisfeiler-Lehman 算法的可微泛化
如果你已經對 GCNs 及其相關方法很熟悉了的話,你可以直接跳至「GCNs 第 Ⅲ 部分:嵌入空手道俱樂部網絡」部分。
圖卷積網絡到底有多強大
近期文獻
將成熟的神經模型(如 RNN 或 CNN)泛化以處理任意結構圖是一個極具挑戰性的問題。最近的一些論文介紹了特定問題的專用體系結構。還有一些根據已知的譜圖理論構建的卷積圖。
來定義在多層神經網絡模型中使用的參數化濾波器,類似于我們所知且常用的「經典」CNN。
還有更多最近的研究聚焦于縮小快速啟發式和慢速啟發式之間的差距,但還有理論更扎實的頻譜方法。Defferrard 等人(NIPS 2016,https://arxiv.org/abs/1606.09375)使用在類神經網絡模型中學習得到的具有自由參數的切比雪夫多項式,在譜域中得到了近似平滑濾波器。他們在常規領域(如 MNIST)也取得了令人信服的結果,接近由簡單二維 CNN 模型得到的結果。
在 Kipf & Welling的文章中,我們采取了一種類似的方法,從光譜圖卷積框架開始,但是做了一些簡化(我們將在后面討論具體細節),這種簡化在很多情況下都顯著加快了訓練時間并得到了更高的準確性,在許多基準圖數據集的測試中都得到了當前最佳的分類結果。
GCNs 第 Ⅰ 部分:定義
目前,大多數圖神經網絡模型都有一個通用的架構。在此將這些模型統稱為圖卷積網絡(Graph Convolutional Networks,GCNs)。之所以稱之為卷積,是因為濾波器參數通常在圖中所有位置(或其子集,參閱 Duvenaud 等人 2015 年發表于 NIPS 的文章共享。
這些模型的目標是通過圖上的信號或特征學習到一個函數
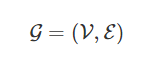
,并將其作為輸入:
每個節點 i 的特征描述 x_i,總結為一個 N * D 的特征矩陣 X(N:節點數量,D:輸入特征數量)
圖結構在矩陣形式中的一個代表性描述,通常以鄰接矩陣 A(或一些其他相關函數)表示
之后會生成節點級輸出 Z(N * F 特征矩陣,其中 F 是每個節點的輸出特征的數量)。圖級輸出可以通過引入某種形式的池化操作建模。
然后每一個神經網絡層都可以被寫成一個非線性函數:

其中 H^(0)= X,H^(L)= Z(或將 z 作為圖級輸出),L 是層數。模型的特異性僅表現在函數 f( , ) 的選擇和參數化的不同。
GCNs 第 Ⅱ 部分:一個簡單示例
我們先以下述簡單的層級傳播規則為例:

式中 W(l) 是第 l 個神經網絡層的權重矩陣,σ() 是一個非線性激活函數如 ReLU。盡管這個模型很簡單,但其功能卻相當強大(我們稍后會談到)。
但是首先我們要明確該模型的兩個局限性:與 A 相乘意味著,對每個節點都是將所有相鄰節點的特征向量的加和而不包括節點本身(除非圖中存在自循環)。我們可以通過在圖中強制執行自我循環來「解決」這個問題——只需要將恒等矩陣添加到 A 上。
第二個局限性主要是 A 通常不是歸一化的,因此與 A 相乘將完全改變特征向量的分布范圍(我們可以通過查看 A 的特征值來理解)。歸一化 A 使得所有行總和為 1,即 D^-1 A,其中 D 是對角節點度矩陣,這樣即可避免這個問題。歸一化后,乘以 D^-1 A 相當于取相鄰節點特征的平均值。在實際應用中可使用對稱歸一化,如 D^-1/2 A D^-1/2(不僅僅是相鄰節點的平均),模型動態會變得更有趣。結合這兩個技巧,我們基本上獲得了 Kipf&Welling 文章中介紹的傳播規則:
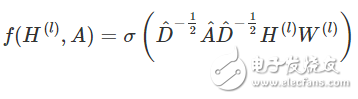
式中 A =A+I,I 是單位矩陣,D 是 A 的對角節點度矩陣。
在下一節中,我們將在一個非常簡單的示例圖上進一步研究這種模型是如何工作的:Zachary 的空手道俱樂部網絡。
GCNs 第 Ⅲ 部分:嵌入空手道俱樂部網絡

空手道俱樂部圖的顏色表示通過基于模塊化的聚類而獲得的共同體(詳情參閱 Brandes 等人發表于 2008 年的文章。
讓我們看一下我們的 GCN 模型是如何在著名的圖數據集上工作的:Zachary 的空手道俱樂部網絡(見上圖)。
我們采用了隨機初始化權重的 3 層 GCN。現在,即使在訓練權重之前,我們只需將圖的鄰接矩陣和 X = I(即單位矩陣,因為我們沒有任何節點特征)插入到模型中。三層 GCN 在正向傳遞期間執行了三個傳播步驟,并有效地卷積每個節點的三階鄰域(所有節點都達到了三級「跳躍」)。值得注意的是,該模型為這些節點生成了一個與圖的共同體結構非常相似的嵌入(見下圖)。到目前為止,我們已經完全隨機地初始化了權重,并且還沒有做任何訓練。
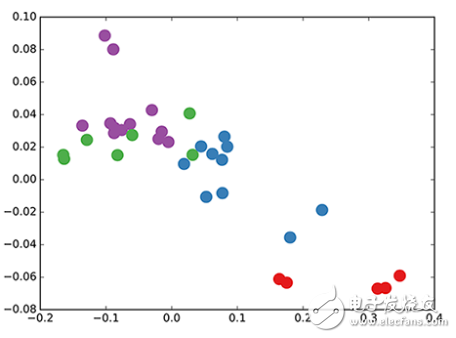
GCN 節點在空手道俱樂部網絡中的嵌入(權重隨機)。
這似乎有點令人驚訝。最近一篇名為 DeepWalk 的模型(Perozzi 等人 2014 年發表于 KDD https://arxiv.org/abs/1403.6652)表明,他們可以在復雜的無監督訓練過程中得到相似的嵌入。那怎么可能僅僅使用我們未經訓練的簡單 GCN 模型,就得到這樣的嵌入呢?
我們可以通過將 GCN 模型視為圖論中著名的 Weisfeiler-Lehman 算法的廣義可微版本,并從中得到一些啟發。Weisfeiler-Lehman 算法是一維的,其工作原理如下 :
對所有的節點

求解鄰近節點 {vj} 的特征 {h_vj}
通過 h_vi←hash(Σj h_vj) 更新節點特征,該式中 hash(理想情況下)是一個單射散列函數
重復 k 步或直到函數收斂。
在實際應用中,Weisfeiler-Lehman 算法可以為大多數圖賦予一組獨特的特征。這意味著每個節點都被分配了一個獨一無二的特征,該特征描述了該節點在圖中的作用。但這對于像網格、鏈等高度規則的圖是不適用的。對大多數不規則的圖而言,特征分配可用于檢查圖的同構(即從節點排列,看兩個圖是否相同)。
回到我們圖卷積的層傳播規則(以向量形式表示):
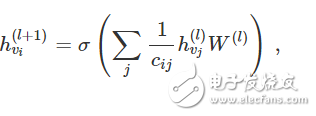
式中,j 表示 v_i 的相鄰節點。c_ij 是使用我們的 GCN 模型中的對稱歸一化鄰接矩陣 D-1/2 A D-1/2 生成的邊 (v_i,v_j) 的歸一化常數。我們可以將該傳播規則解釋為在原始的 Weisfeiler-Lehman 算法中使用的 hash 函數的可微和參數化(對 W(l))變體。如果我們現在選擇一個適當的、非線性的的矩陣,并且初始化其隨機權重,使它是正交的,那么這個更新規則在實際應用中會變得穩定(這也歸功于歸一化中的 c_ij 的使用)。我們得出了很有見地的結論,即我們得到了一個很有意義的平滑嵌入,其中可以用距離遠近表示局部圖結構的(不)相似性!
GCNs 的第 Ⅳ 部分:半監督學習
由于我們模型中的所有內容都是可微分且參數化的,因此可以添加一些標簽,使用這些標簽訓練模型并觀察嵌入如何反應。我們可以使用 Kipf&Welling文章中介紹的 GCN 的半監督學習算法。我們只需對每類/共同體(下面視頻中突出顯示的節點)的一個節點進行標記,然后開始進行幾次迭代訓練:
用 GCNs 進行半監督分類:用每類的一個單獨的標簽進行 300 次迭代訓練得到隱空間的動態。突出顯示標記節點。
請注意,該模型會直接生成一個二維的即時可視化的隱空間。我們觀察到,三層 GCN 模型試圖線性分離這些(只有一個標簽實例的)類。這一結果是引人注目的,因為模型并沒有接收節點的任何特征描述。與此同時,模型還可以提供初始的節點特征,因此在大量數據集上都可以得到當前最佳的分類結果,而這也正是我們在文章中描述的實驗所得到的結果。
結論
有關這個領域的研究才剛剛起步。在過去的幾個月中,該領域已經獲得了振奮人心的發展,但是迄今為止,我們可能只是抓住了這些模型的表象。而神經網絡如何在圖論上針對特定類型的問題進行研究,如在定向圖或關系圖上進行學習,以及如何使用學習的圖嵌入來完成下一步的任務等問題,還有待進一步探索。本文涉及的內容絕非詳盡無遺的,而我希望在不久的將來會有更多有趣的應用和擴展。
 電子發燒友App
電子發燒友App










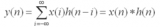

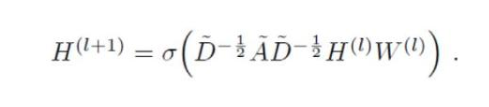
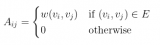













評論