這篇文章非常詳細的講解了寬帶分相網絡（或移相網絡、多項網絡）的設計，這個設計是現有分相網絡的雛形，其基本理論和推導方法非常經典，以供學習參考。

本文發表時間是1950年，作者W. Saraga 是一位德國猶太物理學家，出生于柏林，父親是羅馬尼亞人，母親是俄羅斯人。

The Design of Wide-Band Phase Splitting Networks*

寬帶分相網絡設計*

W. SARAGA?, SENIOR MEMBER, IRE

摘要

近年來，已有許多文章和專利討論了分相網絡的性質和設計，特別是與單邊帶調制器配合使用的情況。然而，它們都限制在特定的設計方法或特定數量的設計參數上。本文給出了對分相網絡的一般性研究結果，分別處理網絡分析、網絡綜合和性能曲線逼近問題。對于最重要類型的曲線逼近，如泰勒和切比雪夫逼近，給出了任意數量的設計參數和任意所需逼近精度的顯式公式。提供了經典全通濾波網絡的替代方案，并且發展了損耗補償相移網絡。通過這種方式，提供了對復雜指標的分相網絡的清晰和相對簡單的設計指南。此外，我們相信其中一些提供的理論結果和開發的方法，例如，泰勒和切比雪夫逼近、損耗補償的方法、網絡綜合的某種方法，以及將逼近曲線表示為兩個變量的迭代函數（迭代指數為分數）是新穎且具有一般理論意義的。

I. 引言

過去十年間，經常討論如何設計分相電路以在寬頻帶上產生恒定的相差。這些電路主要用于載波電話的單邊帶調制器、多相無線電系統、頻移鍵控以及陰極射線示波器的寬帶圓時基。

有趣的是，在早期提及信號頻帶分相的三個參考文獻中，沒有提供直接分相的寬帶網絡，而是使用了輔助的兩相單頻載波源，配合適當的調制器和解調器級聯。 (Wirkler,? Vilbig? )。早在1925年，Hartley? 描述了一個由兩個具有不同截止頻率和不同級數的濾波器組成的寬帶分相網絡。Honnell? 和 Lenehan? 描述了非常簡單的寬帶分相電路，但沒有提供恒定幅度輸出。由Byrne?、Loyet?、Hodgson?、Dome?、Norgaard? 和 Luck? 描述的寬帶分相電路由兩個具有恒定輸出幅度的相移網絡組成。

Byrne和Loyet提供了各種分相電路的理論和測量的指標性能，但沒有提供任何設計信息。另一方面，Hodgson詳細討論了設計方法。他的主要建議是分別設計每個相移網絡，以使其在相關頻帶上的相移與頻率的對數成線性關系，即，其中和是常數。如果對于兩個網絡是相同的，但對于每個網絡是不同的，比如和，那么兩個相移和的差值是，即為所需的常數。Dome遵循相同的一般思路，但Hodgson的討論主要是在格型和橋相移網絡方面，而Dome描述了一些對經典格型網絡的有趣替代方案。在Hodgson的專利中，兩個相移網絡的個體性能是分別標定的；Luck討論了分相電路的設計和性能作為一個整體。這是一個重要的進步。但是，Luck只考慮了具有四個設計參數的網絡。

本文的目的是研究具有任意數量的設計參數、任意期望帶寬和任意接近期望理想性能的分相網絡。 行文將按以下順序進行：(1)網絡分析，(2)性能曲線逼近，(3)網絡綜合。將發現獲得具有一般有效性和適用性的結果相對容易。在許多方面，需要解決的問題類似于或與在濾波器設計的綜合方法和理論開發中遇到的問題相同。然而，在由恒定阻抗電路組成的分相電路的情況下，解決這些問題比濾波器設計的情況更容易，因為不會出現不匹配所引起的復雜問題。此外，恰好在橢圓函數變換理論中，這對濾波器以及分相電路設計都適用，對于分相電路設計的變換比適用于濾波器設計的變換更簡單。

II. 基本電路

圖1所示顯示了一個由兩個相移網絡組成的分相電路，它們在輸入端并聯。在我們研究的初期，假定相移網絡是傳統的全通恒阻單級點格型網絡，其串聯臂的電抗分別為? 和?，格臂的電抗分別為? 和?。

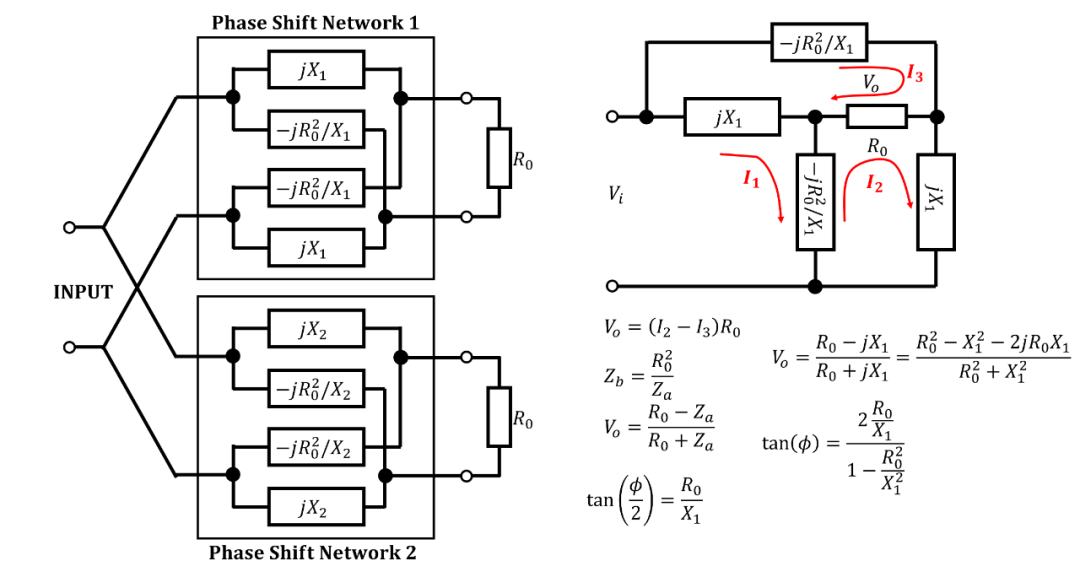
圖1. 基本的分相電路

譯注：圖1經過重繪，右邊是對其中一個移相網絡進行分析，經過驗證，角度公式和圖有出入，問題應該在輸出的極性上，將電壓極性反轉就可以得到式(1)。

然后，網絡分別產生的相移? 和? 由以下公式給出

因此，相移差? 由以下公式給出

如果?，。因此，在理想的? 分相電路中， 應為1，或?。

與1的偏差大小的重要性只能通過參考分相電路的特定應用來討論。考慮使用分相網絡的單邊帶調制器是有意義的。如果假定所有幅度和相位關系都完全符合要求（見圖2），

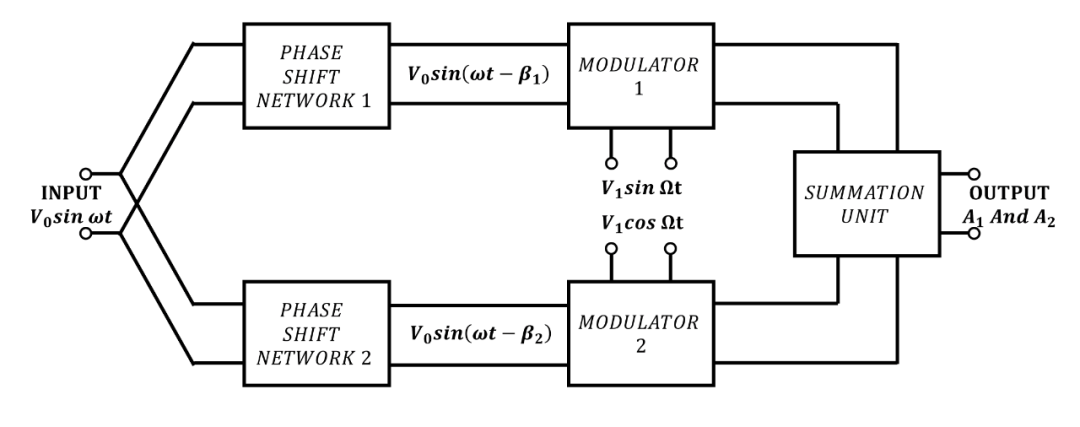
圖2. 使用分相電路的單邊帶調制器

但不完全為1，可以顯示所需的邊帶幅度? 和抑制的邊帶幅度? 由以下公式給出：

其中? 是相位差? 與? 的偏差，即

其中? 是? 時? 的值。

譯注：這里可以推導出總輸出公式：

代入式(4)得到：

式中求和第一項為上邊帶，也即所需邊帶(式(3a)中表示誤差對所需邊帶的抑制，越小越好)，第二項為下邊帶，即為所抑制的邊帶(式(3b)中表示誤差對抑制邊帶的抑制，越大越好)。將式(4)代入式(2)可以得到式(5):

如果給定了?，我們可以通過以下公式直接獲得? ：

將（3a）和（3b）與（5）結合起來，我們可以獲得? 和? 作為? 的函數。結果已在圖3中繪制。

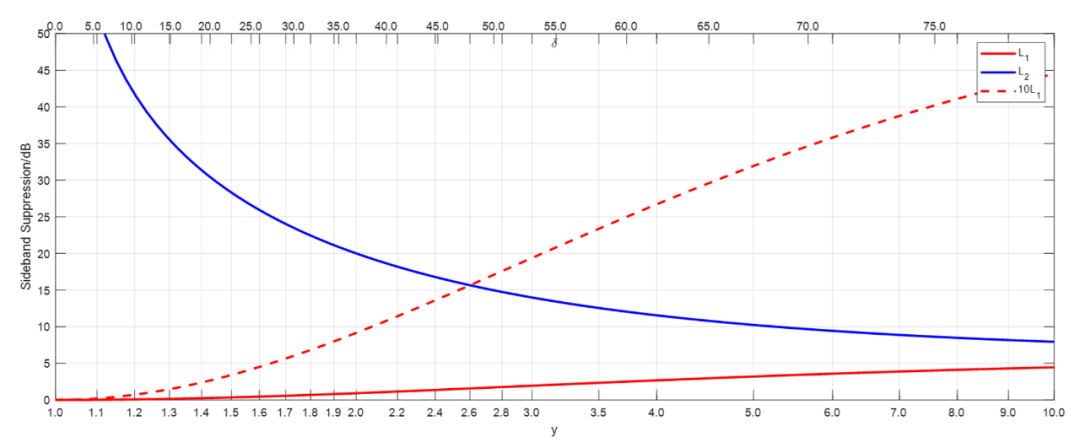
圖3. 輸出（所需和需抑制的邊帶）作為相位與? 偏差和的函數

要注意，轉換? 使? 和? 保持不變，并將? 轉換為?。

式（2）與源電阻? 和負載電阻? 之間的格型濾波器的插入損耗? 的計算中出現的表達式非常相似，其中串聯臂電抗為?，格臂電抗為?。我們發現

譯注：式(6a)和(6b)推導如下，依據格型網絡傳遞函數公式：

令且代入上式得到：

求其幅度值：

和式(6)結果一致。這個結果表現出兩格型網絡分相的相位變化和單個格型網絡的幅頻響應有類似性。這里作者非常巧妙的由相頻曲線直接類比到了幅頻。

注//en.wikipedia.org/wiki/Lattice_network

通過比較（6b）和（2），可以看出? 和? 分別從電抗? 和? 中以相同的方式形成。這種相似性對于分析和綜合分相網絡具有重要意義，并將在后續討論中使用。

III. 網絡分析

本節的目標是為網絡設計和綜合找到函數? 的一般特性，作為必要的準備，該函數由式(2)定義，如果? 是從物理可綜合網絡得到。由于

我們從? 和? 的特性討論開始。從式(1)中可以得出，作為歸一化頻率? 的函數， 和? 必須滿足 Foster 的電抗定理；例如，它們必須是? 的奇有理函數；所有的極點和零點都是簡單的，并且出現在實頻率上；零點和極點是交替的；在? 和? 時，只允許0或這兩個值。每個表達式的分母和分子的次數差1。

是一個限制較少的函數。像? 和? 一樣，它是? 的奇有理函數，在零和無窮頻率時為零或無窮。但是它的零點和極點不需要交替或出現在實頻率上，分母和分子的次數可以相差很大。

這直接來自于式(7)，并且由于式(6b)，對于? 和? 同樣有效。現在只處理?，因為要求? 在從 到? 的帶寬上近似等于1，顯然不允許在這個帶寬內有? 的任何極點或零點。另一方面，我們已經看到在? 和? 時， 將是0或，因此? 將傾向于對于非常大和非常小的? 值偏離1。因此，建議（參見，例如，Hodgson? ），除了0和，實? 值不應出現任何極點或零點，因為這樣的極點或零點會增加? 從1的偏離；0和 處的極點或零點應為1次。然后，分子和分母的次數必須相差1。我們將在下一節中看到，泰勒和切比雪夫逼近將滿足符合此約束的表達式。

在接下來的內容中，我們將假設在? 時，我們有?。然后? 將呈現以下形式

其中? 或 1 ，并且常數? 和? 以及? 都是正實數。我們將用? 表示在? 中出現的? 的最高次冪，并且我們將在后面看到，逼近階數也可以用? 表示。式（8a）也可以寫成以下形式

其中所有的? 和? 都是實數。當? 作為? 的函數關于?(即?)是對稱時，出現了一個重要的情況，如果? 是奇數，變換? 導致?；但是如果? 是偶數，它將保持? 不變。下面列出了當? 是對稱且?值從 1 到 6 時的? 的表達式：

以上公式為分析網絡提供了基本的框架，并為接下來的網絡設計和綜合奠定了基礎。通過這些公式，我們可以更好地理解分相網絡的基本特性和參數，為進一步的研究和分析提供了重要的參考。

譯注：上面的式8(c)實際上是對擬合的波形做了一個約束：

是一個有理多項式的比(可實現性)

當時，(可實現性)

當時，(濾波器的通帶部分，保證相位90°的條件)

當為奇數時，當時，函數(關于(1,1)中心對稱)

當為偶數時，當時，函數(關于軸對稱)

通過以上約束條件可以求出式(8c)，這里以舉例說明：

由式(8a)可知

令得到：

上面兩式相等得到：

這樣得到式(8c)的表達式。

IV. 所需性能曲線的逼近

在本節中，我們將討論尋找使得?, 或? 在范圍? 到? 內成為逼近1的最佳近似的常數值的方法。如果需要的其他值，比如，那么在接下來的討論中，必須替換為。我們將從泰勒(Taylor)和切比雪夫(Tchebycheff)近似開始，因為在這里可以超越逼近方法的推薦，給出明確的公式，這些公式可以根據?（即? 的范圍）給出常數。

在本節中，我們將討論在表達式，或中尋找這些待定常數值的方法，使得在從到的范圍內成為對1的良好近似。如果需要的其他值，比如，則在接下來的討論中，必須替換為。在討論泰勒和切比雪夫近似時，我們不僅可以推薦這些方法，更能進一步得出具體的公式來明確表達常數，這些公式用表示常數，如用的范圍表示常數。

1. 泰勒逼近

第階的泰勒逼近的特點是存在個設計參數，它們被選擇成這樣的值，以便對于指定的值，比如說，本身和前個微分系數，對于，對于所需曲線和逼近曲線是相同的。因此，越高，逼近曲線越接近所需曲線。

如果我們假設，那么第階的泰勒逼近由下式給出：

通過將式(9a)寫成下面的形式：

譯注：這里突然冒出來的(9a)公式實在是沒有理解，查閱相關資料得到：

可以看到這個和切比雪夫多項式非常類似，有人對其進行了推導：

這個公式在處對y=1進行了非常好的逼近，如下圖(4a)給出了的函數圖像。

我們看到在中出現的的最高次數是，并且是關于對數頻率刻度對稱的奇有理函數。

將其寫成如下形式：

我們可以很容易地證明（令 和? ），在處的前個微分系數為零，這符合對的泰勒逼近的要求。下面列出的的表達式：

這些曲線在圖4(a)中用對數-對數坐標繪制，

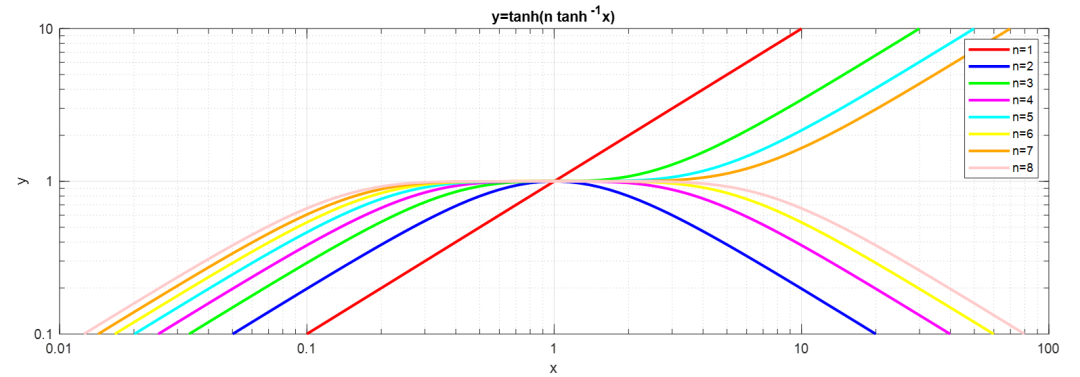
圖 4(a) 泰勒逼近

對于范圍從到，即對于。例如，這對應于頻率范圍從到。

從(9b)中可以看出，如果被替換，對于偶數值保持不變，并且對于奇數值被替換。與的偏差隨著的增加而增加。如果范圍的限制表示為和，并且范圍的限制表示為和，則作為的函數由下式給出：

就函數關系而言，這與(9a)相似。如果我們以下面的形式寫出(9e)：

我們可以看到，如果我們為和使用由函數定義的刻度，那么作為的函數可以表示為通過坐標系原點的直線，對于任何值，斜率為。這已在圖4(b)中示出來。

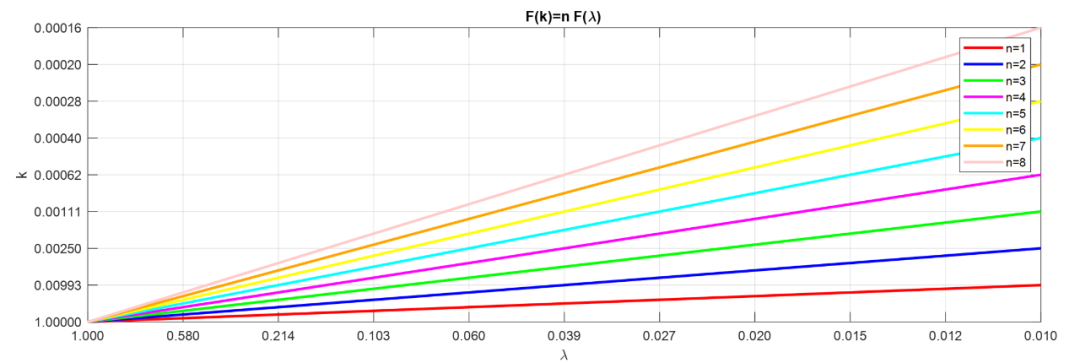
圖 4(b) 泰勒逼近與所需性能的偏差

考慮到(9f)和(9a)之間的功能相似性，圖4(b)也表示作為的函數，換句話說，圖4(b)可以看作顯示與圖4(a)相同的曲線。可以看到，如果是給定的，那么隨著的增加而減小，即的范圍變得更小。

為了綜合具有由式(9a)所描述性能的網絡，我們必須找到（如將在第V節中解釋的）時的值。它們由下式給出：

2. 切比雪夫逼近

切比雪夫逼近的特點是出現的最大偏差是最小的。橢圓函數的變換理論非常方便地描述了關于的對數-軸對稱的關于的奇有理函數，在范圍到內，以切比雪夫的方式逼近，值在范圍和內。如上所述，的這些限制等效于相位差的偏差從所需值的最大和最小偏差和，以及。使用Cayley的符號，可以很容易地證明階的切比雪夫逼近由下式給出：

在由(10a)和(10b)定義的有理函數中出現的的最高次數是。Cayley用后綴'1'表示和，以表示從模數到較大的模數的"第二變換"。然而，在接下來的討論中，很多情況下使用后綴來表示變換的順序是方便的。因此，為了避免混淆，將不使用Cayley的后綴'1'。為了本討論的目的，有時也方便地表示為。在式(10a)和(10b)中，是由(10b)定義的輔助變量，而是由(10a)通過定義的。已在上面定義過。可以從得出和如下：是的函數，比如說是橢圓函數理論中已知的（例如由Hayashi1編制的表格表示的函數，即。可以通過下面的關系從獲得：

接下來，如果給定，隨著的增加，會減小，即的范圍變得更小。此外，可以在Hayashi的表中找到作為的函數，以及作為的函數。然后由下式給出：

譯注:這里使用的雅克比橢圓函數與一般的橢圓函數濾波器所使用的方法不同，這里利用了橢圓函數的雙周期特性，讓橢圓函數往虛軸方向平行擺放對齊，再使用虛軸一側實現等紋波特性。可以將公式寫為更為緊湊的形式：

下圖式時平面零極點分布圖：

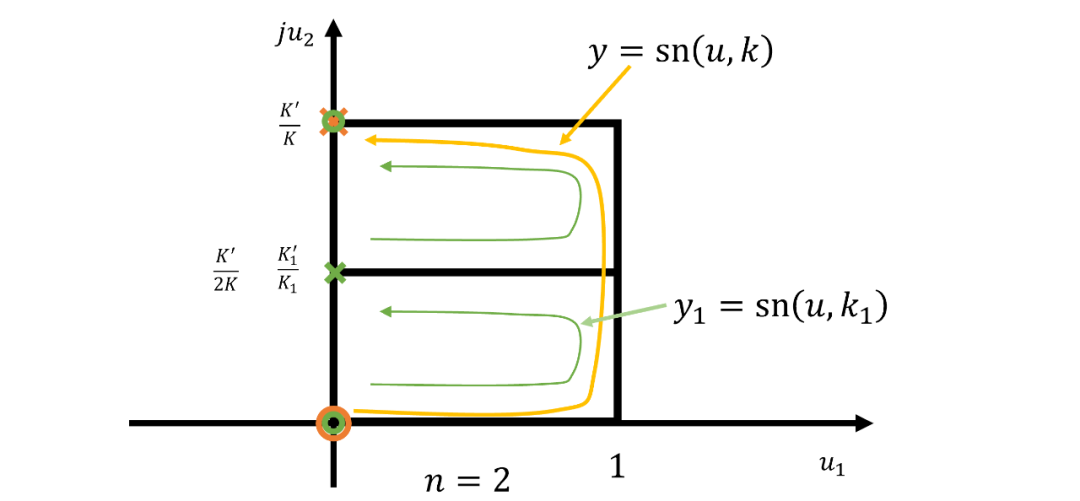
表 Ia切比雪夫逼近法；和作為的函數。

下表和圖顯示了作為以的函數的情況：

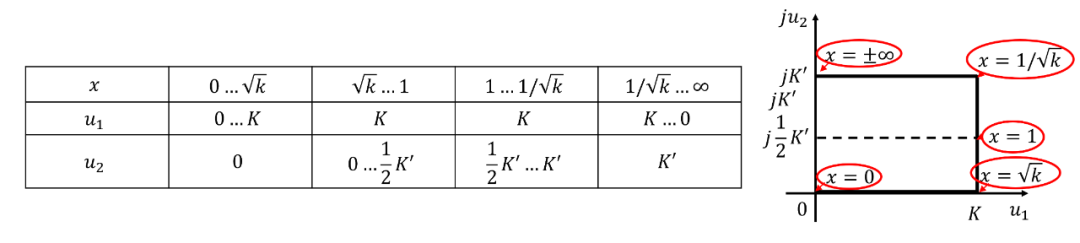
比(10b)更好的一個形式：

給出作為的函數的最佳表達式，如果

因此，可以為任何和得到，并且，當被指定時，可以選擇以使（表示從0的最大偏差）盡可能小。作為和的函數在圖5(b)中表示。由于(10c)的形式與(9f)相同，因此如果對和使用線性刻度，再次可以將曲線繪制為斜率為的直線。應該注意，在切比雪夫逼近的情況下，關聯到的曲線（圖5b）并不同時關聯到。可以看出，對于任何給定的和值，從圖5(b)獲得的值，即對于切比雪夫逼近法，比從圖4(b)獲得的值，即對于泰勒逼近法，更接近1。

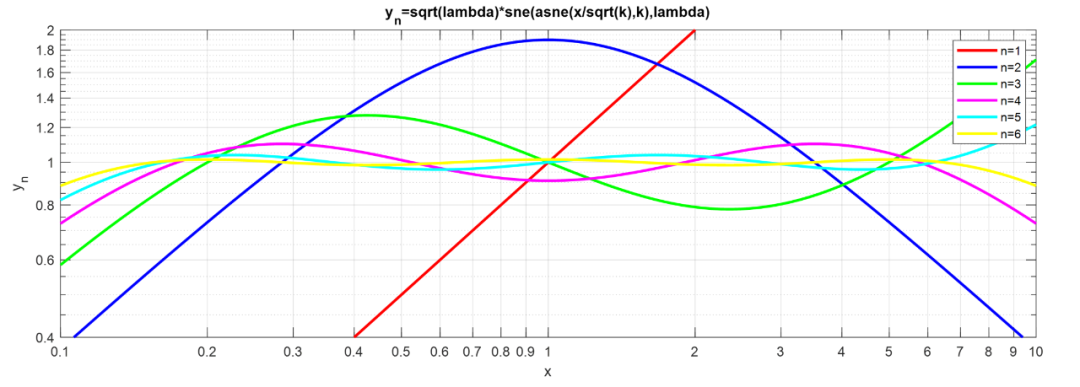
圖 5(a) 切比雪夫逼近法。

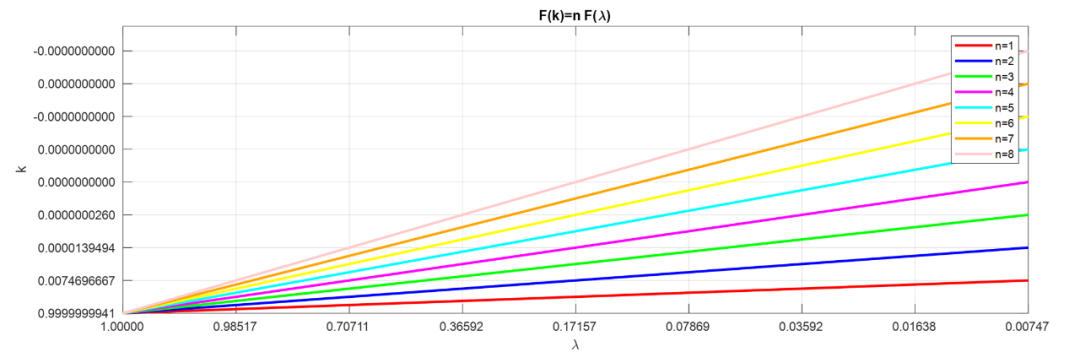
圖 5(b) 切比雪夫逼近法與所需性能的偏差。

作為的函數可以通過橢圓函數的表格直接從(10a)和(10b)中評估，例如，Milne-Thomson的表格和Hayashi的表格。為此，式(10a)和(10b)可以按照表I(a)中顯示的方式進行修改。圖5(a)示意性地顯示了的切比雪夫逼近，其中的范圍從到，其中。對于這些圖表，沒有使用表中給出的公式。僅評估了出現最大值或最小值的值以及的值，并且已經畫出了通過這些點的曲線。然而，對于（見第VI節），大量點的數值檢查顯示了與繪制的曲線非常好的一致性。曲線呈振蕩行為，所有的最大值和最小值分別發生在值和處，的值取決于所考慮的值和值。對于偶數值，有個最大值，個最小值，兩個與線的交點和個與線的交點。對于奇數值，有個最小值和個最大值，一個與線的交點，一個與線的交點和個與線的交點。

為了能夠繪制的這些特征點，我們必須知道和時的值。另一方面，為了能夠以式(8c)的形式將寫為的有理函數，我們必須知道和時的值，以及在偶數值的情況下的值（見下文）。最后，為了綜合一個根據的性能曲線的網絡，我們必須找到時的值。所有這些的值可以通過首先反轉(10a)來找到作為的函數，然后將的這個表達式代入(10b)中得到。然而，為了簡化切比雪夫逼近法的工程應用，列出了變為,? 和?時的值，分別在表I，II和III中。列表中的表達式形式規則，如果需要，很容易通過類推將表格擴展到任何值。上文提到的值由下式給出：

表 Ib切比雪夫逼近； 作為? 的函數。

令?，則

?

?

此表在表II和III中有更詳細的說明。

在處理切比雪夫逼近時，通常很方便使用對這些逼近有效的“指數定律”。令? 表示在范圍? 到?上對? 的第階逼近，并且讓? 表示? 的變化范圍，即， 在? 和? 之間變化。此外，讓? 表示在? 范圍? 到? 上對? 的第階逼近，并且讓? 表示? 的變化范圍，即， 在? 和? 之間變化。那么，當從變化到時，將視為的函數與范圍到上對的第階逼近是相同的，如果。這可以通過以下公式表示：

憑借指數定律，如果我們已經探討了的情況，我們可以將所有獲得的結果應用于? 和?。如果我們已經探討了和，我們可以結合結果以獲得 和?的情況。指數定律的一般化解釋將在附錄中給出。

表 II

切比雪夫逼近；對于的。

?

?

表 III

切比雪夫逼近；對于的。

?

?

3. 切比雪夫逼近的替代理論

到目前為止，我們已經使用橢圓函數討論了切比雪夫逼近的理論。這導致了最簡潔和最通用類型的表達式。同時，必須認識到許多工程師不熟悉橢圓函數，并且有時很難獲得良好的橢圓函數表。因此，重要的是要注意，有可能純粹代數地制定逼近法，而無需使用橢圓函數。在實踐中，結合兩種方法，適用于正在考慮的特定案例，有時是最佳選擇。對于，代數理論實際上非常簡單。從開始，可推出以下關系：

對于和；

對于。

條件得到和。對于的這個值，是范圍的第二階切比雪夫逼近。可以通過應用指數定律來討論和的情況。結果列在表IV中。

表 IV

對于? 的切比雪夫逼近; 代數關系

?

?

對于?，推導? 的表達式沒那么簡單。我們從形式為? 的表達式開始，為了使其關于? 對稱，簡化為?。接著我們需要確定? 的值，以便在給定的范圍? 內， 以切比雪夫方式呈現。要求當? 時， 等于?；此外，在未知的? 值，比如說? 處， 的值也應為? 的最小值。因此

必須等于?。比較系數，我們得到三個方程：

如果我們引入?(由Cayley提出的術語)

我們發現

和

式(13a) 和 (13b) 以? 的形式確定了? 和? （ 也可以通過橢圓函數的表格或像圖 5(b) 中的圖表來確定）。接著我們可以找到?。因此我們知道? 是? 的函數以及以下的細節：

如果我們在討論? 的情況時，將獨立變量? 替換為二階逼近?，并將? 替換為?，我們將得到六階逼近，并通過重復這個過程，我們可以得到十二階逼近。如果在討論? 的情況時，我們將? 替換為?，并將? 替換為?，我們將得到九階逼近。然而，對于質數? 等，代數理論變得逐漸困難（參見 Cayley）。

譯注：前述的代數計算方法類似暴力計算，基本思想是函數曲線關于1對稱且等紋波起伏，然后利用對稱性計算其他相關階數的表達式。

4. 通過其他方法逼近

在大多數情況下，關于分相網絡性能的要求可能可以通過前一節討論的切比雪夫或泰勒逼近來滿足。然而，有時可能會一些額外的設計約束，對于這些約束，這些類型的逼近并非最佳可能的解決方案。然后需要一些其他類型的逼近。

如果要求在的個特定值處具有精確的相位差，則可以通過解? 個線性方程組來獲得滿足這些要求的函數? 的參數。Zobel? 已經詳細討論了這種方法，參考了衰減均衡器和相移網絡的設計。應用于分相網絡的設計不會有任何新的問題。

Zobel 建議不僅在指定了多個點的性能的情況下使用這種方法，而且在需要對整個? 值范圍進行良好逼近的情況下也使用這種方法。然而，在這種情況下，Zobel 的方法通常會導致失望的結果（參見例如 Saraga? 和 Baum? 的評論），而且更傾向于使用圖像進行曲線擬合的方法。

對圖形曲線擬合方法的研究顯示，它們可以方便地分類為曲線求和或曲線移位和成形方法(curve shifting and shaping methods)（參見 Saraga?）。通常需要轉換指定所需性能曲線及其容差帶的坐標系，以便可能應用這些圖形方法。在求和方法中，通過在不同位置添加多條標準曲線獲得符合容差帶的曲線。從這些位置可以獲得逼近曲線的參數（例如，參見 Laurent, Rumpelt,? Saraga,? Scowen,? Baum?）。在移位和成形方法中，只能用于有限數量（不超過 4 到 5）的參數，通過比例變化和剪切移動和成形一個單一的標準曲線，直到它符合所需的容差帶（參見 Pyrah,? Truscott,? Saraga?）。我們不在這里討論這些方法應用于分相網絡的特定問題。

V. 網絡綜合

在這一節，我們假設已經以某種方式確定了合適的性能函數。下一步是確定兩個相移網絡，這些網絡將產生這個函數。要解決的問題是當

已知時，找到和。由于在對稱濾波器的設計中也出現了這個問題（見公式（6b））

給出和，并且必須找到物理上可實現的電抗，我們可以將其解應用于我們的問題。Darlington?給出了確定電抗的以下指導（在此根據本文中使用的符號進行了修改）：將寫成的形式，其中和是的多項式。然后將表示為的形式，其中是的偶次多項式，使得的根（即）具有負實部。那么和。

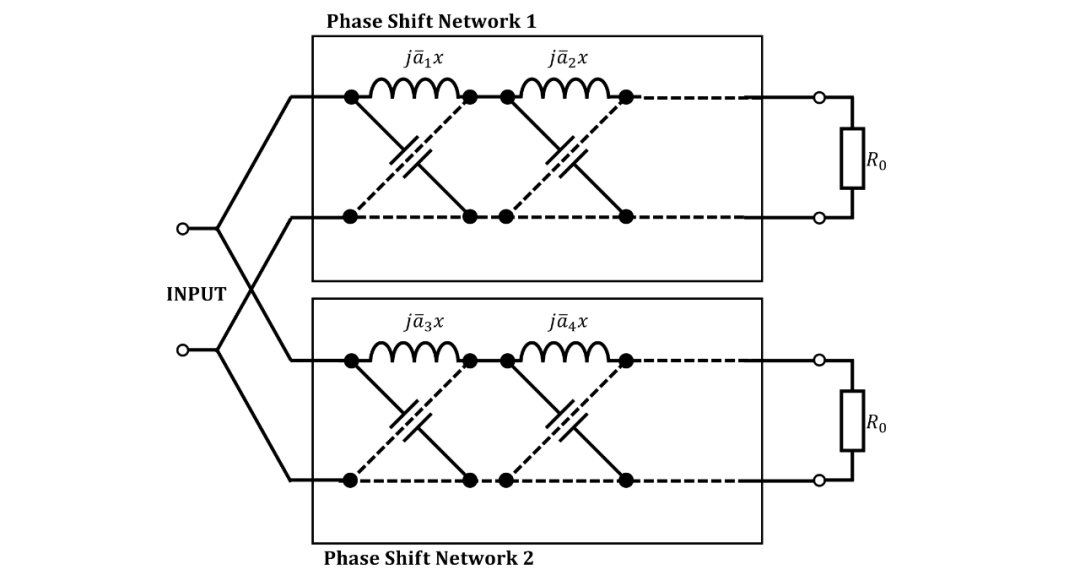
圖 6. 基本分相電路，分解成基本相移段。

Darlington 的方法，雖然沒有明確的證明，但可以以包括證明的方式進行修改。為此，我們考慮在? 的? 值；在這些值，比如說?，相位差? 接近?，這必須是由于? 趨向于? 或? 趨向于?。現在假設兩個基本相移網絡具有串聯電抗? 和?（參見圖 1），由串聯的“基本”相移段組成，每個段的特征是其相移? 和其歸一化的串聯臂電抗? 或其歸一化的串聯臂電感?（參見圖 6）。 然后在每個? 處，這些基本相位角之一? 必須趨向于?，并且?，如果? 是? 的組成部分，或趨向于? 并且?，如果? 是? 的組成部分。由于?，我們發現?。我們選擇使?，歸一化的電感，為正的符號。如果為了獲得正的?，我們必須采取正符號，則相應的? 是? 的組成部分，而在另一種情況下，我們得到了? 的組成部分。通過這種方式，我們不僅找到了? 和?，而且同時也找到了組成兩個基本相移網絡的基本段。可以證明，根據正切函數的加法定理，從基本相移段的電感中形成? 和? 的表達式會導出由 Darlington 給出的表達式。

將看到， 個基本段導致? 中? 的最高次數為?，反之亦然。因此，網絡元件的數量隨著? 的最高次數的增加而增加。

譯注：上面給出了綜合的基本方法，其基本方法是找傳遞函數的"特征值"上，即極點，這些極點剛好是的解，而一個對稱格型網絡電路中又有，在橢圓函數中也可以很方便的求出極點，所以，通過極點將相位和器件值所關聯，從而可以綜合出所需電路。

VI. 兩個實用設計示例

選擇實際示例以供本文討論時，最好選擇非常簡單的示例，因為這樣可以最清楚地展示獲得網絡的方法。首先，我們將討論一個需要泰勒近似的案例，我們選擇一個簡單的案例，即?。然后，最佳逼近由

給出（參見式（9d））。由于? 是奇數，兩個相移網絡的段數必須相差1。假設帶有? 的網絡由兩個段組成，分別具有串聯臂電感? 和?。那么具有? 的網絡有一個單獨的段，例如帶有串聯臂電感?。因此我們得到

和

在這種簡單情況下，我們可以通過比較（14）和（15）中的系數來獲得?。那么?；

代入計算，我們得到了一個關于? 的三次方程，其中一個正根是：。然后?，并且? 和? 可以互換。在更復雜的情況下，我們將解方程?，并通過方程? 或代數方法得到三個根? 和?。根據根的符號，第一個必須對應于?，其他兩個必須對應于?。因此，我們像前述一樣得到? 和?。

譯注：上述綜合原理圖如下：

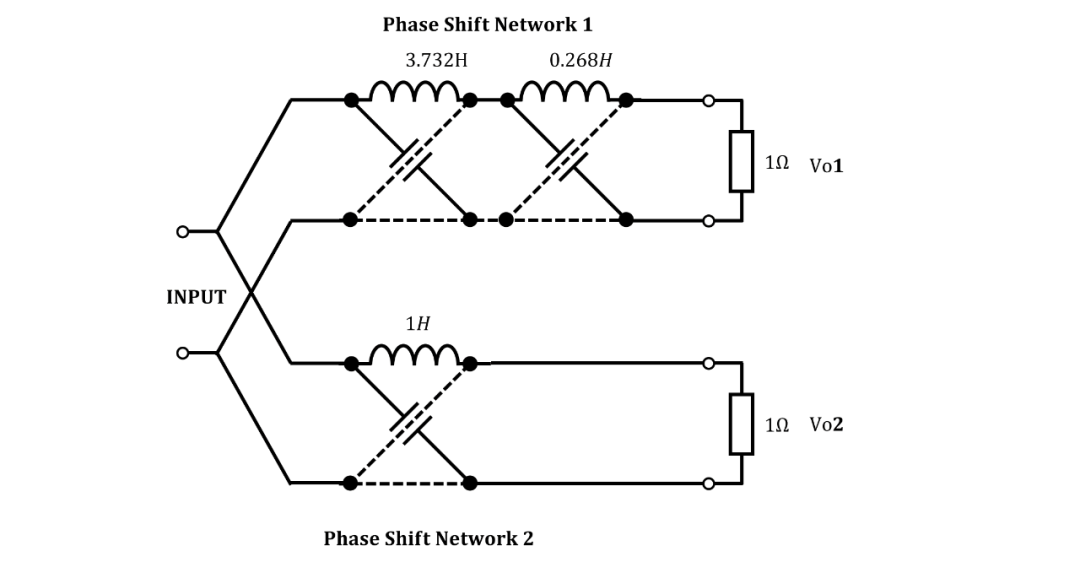
仿真得到和的輸出相頻以及相頻差圖如下：

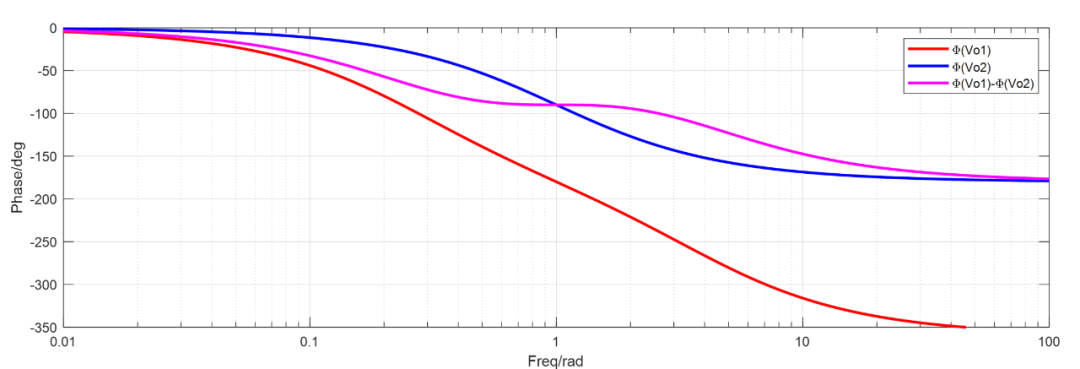
作為第二個示例，我們將討論一個需要 Tchebycheff 逼近的示例。我們將取?，以便我們可以使用代數方法以及橢圓函數的變換來獲得網絡元件。指定的? 范圍假定為從? 到?，其中?。這對應于頻率范圍從? 到?。然后通過 Hayashi 的表格，找到? 為 0.5959。 曲線顯示在圖 5（a）中。表 II 給出了? 時四個? 值的表達式。然后使用 Milne-Thomson 的表格，我們找到?,?。然后對于一個相移網絡? 和對于另一個網絡?。從? 的這些值中，我們發現

和? 和? 可以互換。

應用代數理論，我們從表 IV 中得到

和

與之前相同。

譯注：這里通過值查表的過程可以很方便的使用matlab函數實現(實際上就是找到滿足兩個橢圓函數在平面對齊的條件)：

?

?

n = 4;
k = 0.003;
lambda = ellipdeg(n, k);

>> 
lambda = 0.5959

?

?

求解的值使用matlab也非常方便：

?

?

[K,Kp]   = ellipk(k);
a_bar    = zeros(1, n);
for ii=1:n
    a_bar(ii) = sqrt(k)*sne(1i*(1+4*(ii-1))/(2*n)*Kp/K, k);
    fprintf('a_bar(%d) = %0.5f j
', ii, imag(a_bar(ii)));
end

>>
a_bar(1) =   0.05618 j
a_bar(2) =   2.46908 j
a_bar(3) = -17.79989 j
a_bar(4) =  -0.40501 j

?

?

綜合得到的電路如下：

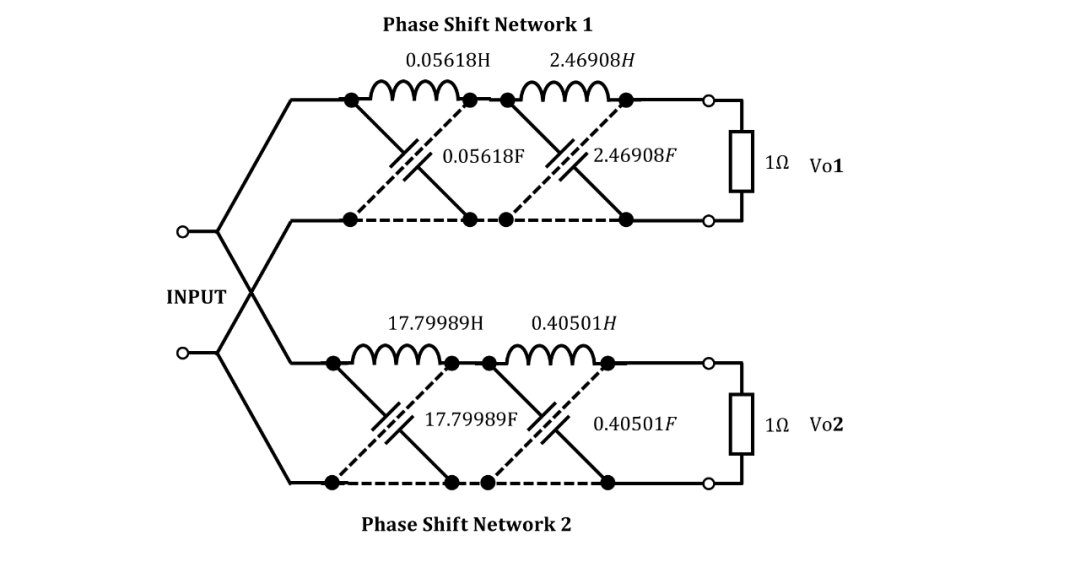
仿真波形如下：

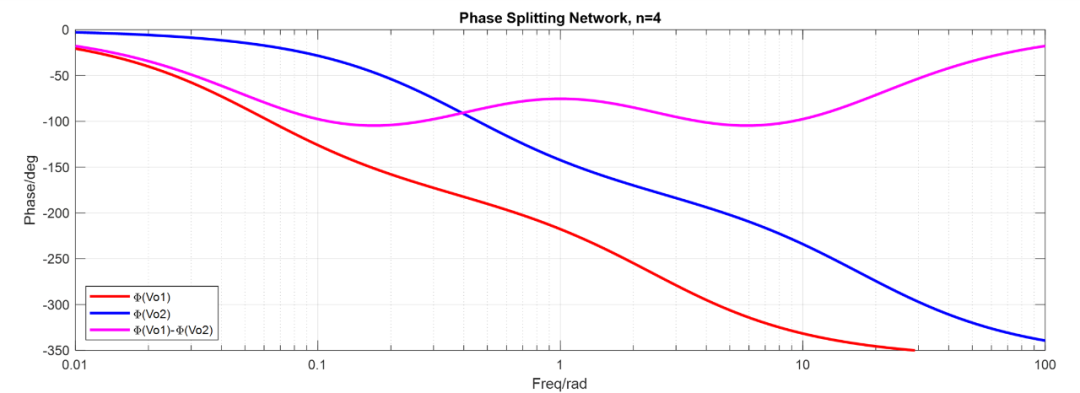
VII. 相移網絡的替代

前面的討論基于傳統的恒定阻抗相移網絡，其串聯臂電抗為? 和格臂電抗為?，插入在等值電阻? 之間。然后相移為?。可以在不改變相移的情況下改變其中一個電阻；然后會產生固定的平坦插損。這在圖7中示出。

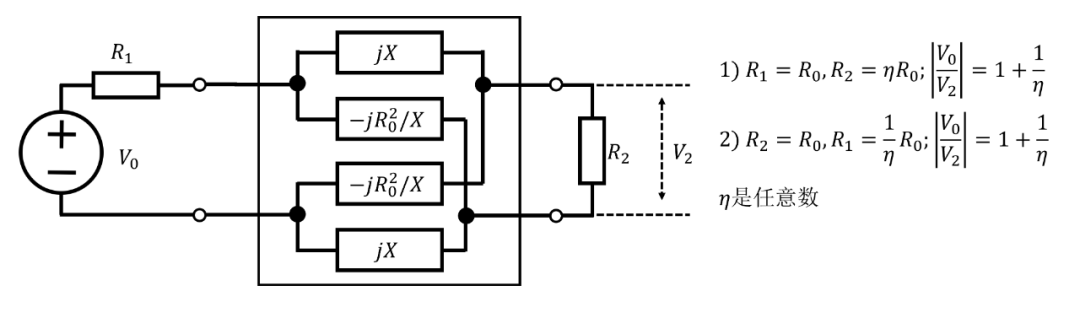
圖 7. 經典相移格型網絡

Marrison? 已經證明，可以用電阻替換兩個格臂電抗，而不改變相移（見圖8）。

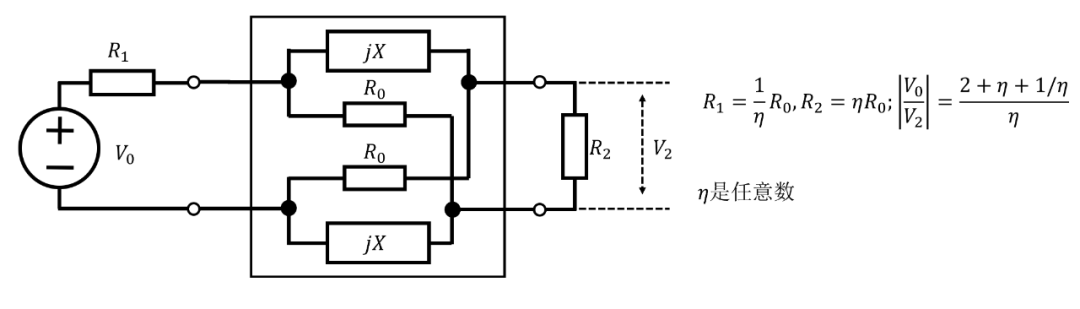
圖 8. 圖 7 網絡的替代方案

然后，如果源阻抗和負載電阻都等于，則產生平坦的插損。可以使源電阻為，負載電阻為。然后產生了取決于的附加平坦插損，但相移仍然不變。Saraga?已經證明，可以用電阻替換剩下的兩個電抗臂中的一個（見圖9），而不改變相移。

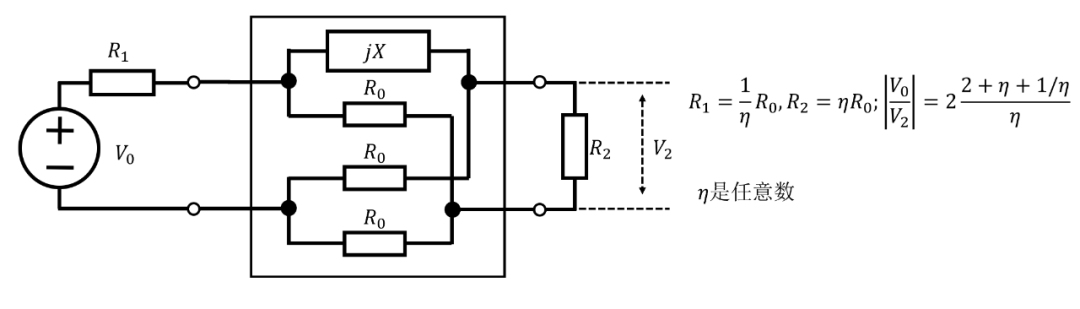
圖 9. 圖 7 網絡的替代方案

然后，如果，固定插損是而不是。兩種其他類型的相移網絡，一種是Nyquist型，由Sandeman?描述（見圖10），

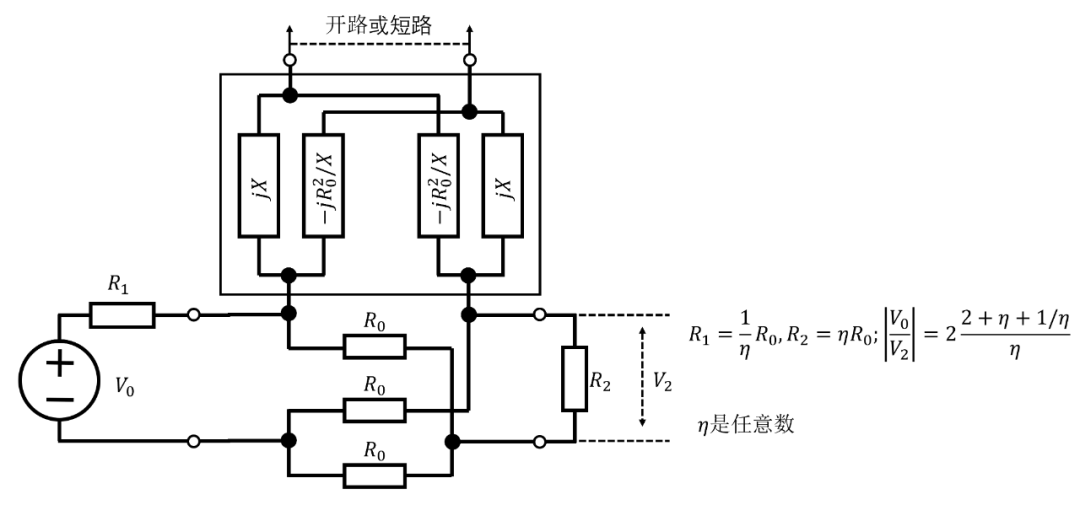
圖 10. 圖 7 網絡的替代方案

另一種由Wald?描述（見圖11）可以被證明是圖9中網絡的特殊情況，但是具有比實際產生相移所需的更多電抗元件。

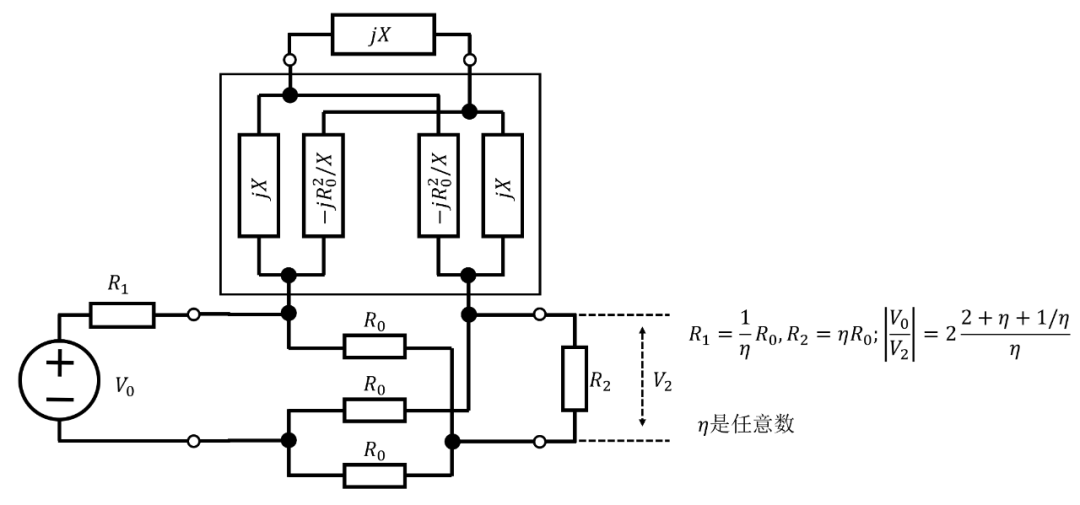
圖 11. 圖 7 網絡的替代方案

圖9中的電路可以用混合電路替換（見Sandeman）。Dome?和Luck?描述了許多所謂的半格網絡，這些網絡由差分源驅動。

VIII. 損耗補償移相網絡

在移相網絡的元件中，損耗效應會扭曲相位特性并產生隨頻率變化的衰減。如果不同元件的? 值不同，阻抗也會受到影響。Starr? 描述了近似補償這些損耗效應的方法。Darlington? 和 Bode? 描述了完美補償損耗效應的方法。網絡的設計是為了滿足預失真的指標，這些指標是通過假設負損耗的發生從原始指標中得到的；然后正損耗產生了所需的性能。這里將描述獲得損耗補償相移網絡的不同方法。

由于任何相移網絡都可以作為單、雙參數相移網絡的串聯組合來構建，因此只需考慮這種網絡的損耗補償就足夠了，該方法的基本思想是僅考慮包含與每個電感串聯的電阻和與每個電容并聯的電阻的網絡，以便這些電阻可以承擔電抗元件的損耗電阻，并設計這些網絡，使它們具有所需的相位特性? 和平坦損耗?。對于圖 12 中的格型網絡，傳遞常數? 由? 給出。

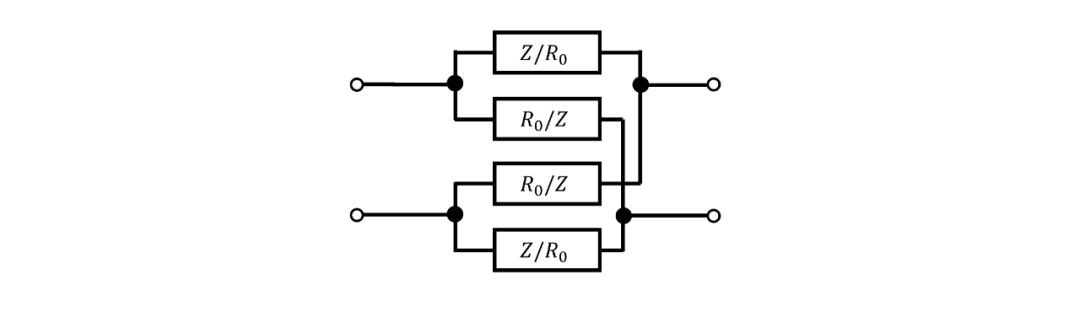
圖 12. 格型網絡，與圖 13 和圖 14 一起顯示以供參考。

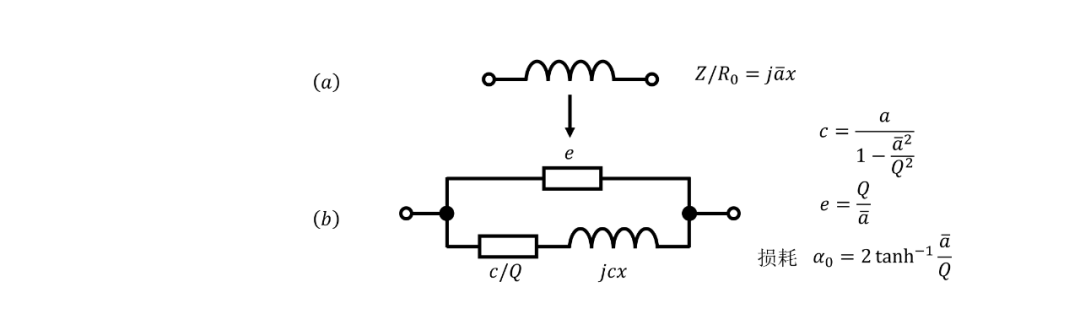
圖 13. 單參數相移網絡的損耗補償。

對于無損耗的單參數相移網絡?（見圖 13(a)），并且?。我們的目標是找到一個阻抗?，其電阻如上所述，使得?，其中?， 是網絡的基本損耗。可以很容易地證明圖 13(b) 中的網絡代表了這種形式的阻抗?。如果? 不是太小，它的元件值將是正的。

現在我們考慮雙參數相移網絡（無損耗），其中? 如圖 14(a) 所示。然后

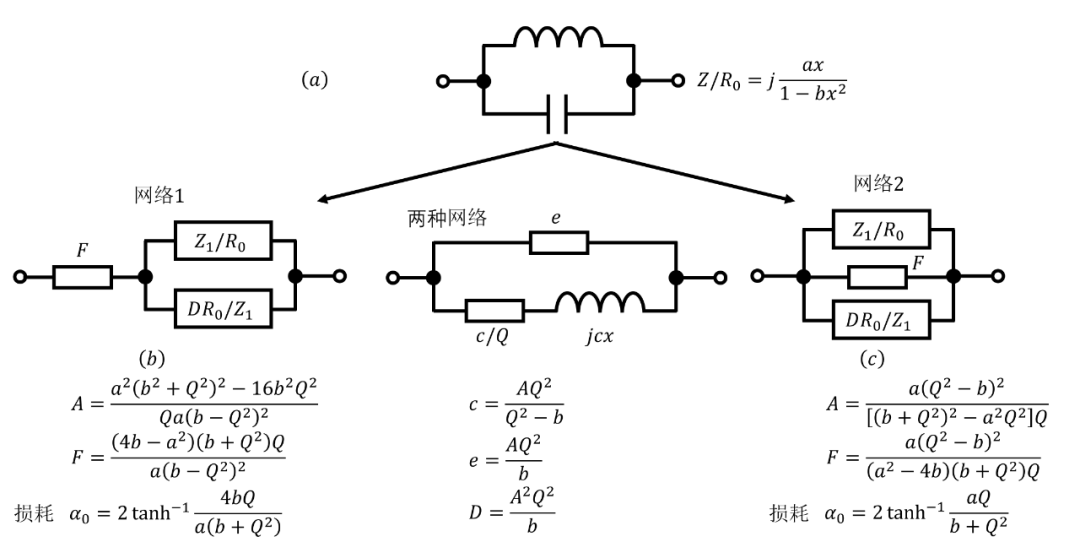
圖 14. 雙參數相移網絡的損耗補償。

我們需要找到一個阻抗?，其電阻如上所述，使得

可以證明，如果滿足圖 14(b) 和 14(c) 中所述的關系，這兩個網絡具有這種阻抗。在圖 14(c) 中，當然可以將電阻? 吸收到? 中。可以看到，如果?，則圖 14(b) 中的電阻? 為負，如果?，則圖 14(c) 中的電阻? 為負。在圖 14(c) 中， 也可能是物理可實現網絡。

如果?，則可以用圖 13(a) 中串聯阻抗定義的兩個更簡單的網絡替換圖 14(a) 中串聯臂電抗定義的相移網絡。如第 V 節腳注 28 所述，只有? 的情況似乎會出現在分相問題中，但這里也處理了另一種情況，因為圖 13 和 14 所描述的三種轉換一起使得可以將任何給定的相移網絡轉換為損耗補償網絡。

注：自撰寫此手稿以來，作者已經看到了 Dagnall 和 Rounds? 以及 Farkas, Hallenbeck 和 Stehlick? 的論文，其中討論了相移網絡的損耗補償的各種其他方法。

附錄

曲線逼近

為 Taylor 和 Tchebycheff 逼近給定? 范圍和給定階數?，式（9e）和（10c）都可以表述為? 與 1 的偏差，可以寫成以下形式：

對于（9e）的情況是：

以及對于（10c）的情況是：

這意味著在兩種情況下， 作為? 的函數可以寫成如下形式：

其中? 表示函數? 的第? 次迭代。這里的“第? 次迭代”不僅指整數值，還包括? 的分數值，因為? 只有在? 是 2 的整數冪時才是整數。Haldane,? Silberstein,? Hadamard. 已經對非整數迭代函數的概念進行了一些討論。

不能以同樣的方式解釋逼近函數? 作為? 的迭代函數，因為? 不僅是? 的函數，還是? 和? 的函數。但是，如果我們將迭代的概念推廣以適用于兩個變量的函數（見 Boole?），則? 可以視為? 的第? 次迭代，其中?。現將說明這一點。

由于? 將兩個獨立變量變為一個依賴變量，只有當我們引入第二個依賴變量時，才可能進行迭代，比如說，一個任意函數?。然后我們將定義? 和? 為函數? 和?。此外，我們可以為整數和非整數值的? 定義迭代函數? 和?，作為滿足以下關系的三個變量? 和? 的函數。

如果我們選擇? 作為任意函數?——恰好與? 無關——我們會看到，如果? 如之前一樣，那么指數法則（式（12））可以按照式（16）的形式表示。換句話說： 和? 可以解釋為? 和? 的第? 次迭代，當它們被視為? 和? 的一對函數。

有趣的是要注意，如果考慮的是多項式逼近而不是有理函數逼近，也可以進行這樣的解釋。如果? 要通過多項式? 在范圍? 到? 中逼近，那么第? 階 Tchebycheff 逼近為

且第? 階偏差?。很容易證明? 和?。這些以及與非整數功能迭代相關的其他問題都在作者正在準備發表的數學論文中進行了處理。

致謝

感謝 J. G. Flint，Telephone Manufacturing Co. 的首席工程師，允許發布此論文。作者還想感謝 Miss L. Fosgate 制作了圖紙，以及 Miss L. Fosgate 和 Miss J. Freeman 執行和檢查了大量的計算。非常感謝 Milne-Thomson 和 Hayashi 由 Scientific Computing Service Ltd., London 提供的橢圓函數表。

參考文獻及腳注

Decimal classification: R246.2? R143. Original manuscript received by the Institute, August 1, 1949.
? Research Laboratories, Telephone Manufacturing Co. Ltd., London, England.
? British Patent No. 301,362, dated August 27, 1927.
? Walter H. Wirkler, U.S. Patent No. 2,173,145, dated Nobember 26, 1937.
? F. Vilbig, "Experimentelle Untersuchung der Verschiebung eines theoretisch beliebig grossen Frequenzbandes um einen bestimmten Phasenwinkel," Telegraphen-Fernsprech-und Funktech., vol. 27, pp. 560-561; December, 1938.
? Ralph V. L. Hartley, U.S. Patent No. 1,666,206, dated January 15,1925.
? M. A. Honnell, "Single-sideband generator," Electronics, vol. 18, pp. 166-168; November, 1945.
? B. E. Lenehan, "A new single sideband carrier system," Elec. Eng., vol. 66, pp. 549-552; June, 1947.
? John F. Byrne, "Polyphase broadcasting," Trans. Elec. Eng., vol. 58, pp. 347-350; July, 1939.
? Paul Loyet, "Experimental polyphase broadcasting," Proc. I.R.E., vol. 30, pp. 213-222; May, 1942.
? K. G. Hodgson, British Patent No. 547,601, dated January 31 1941.
? R. B. Dome, "Wide-band phase shift networks," Electronics, vol. 19, pp. 112-115; December, 1946.
? Donald E. Norgaard, "A new approach to single sideband," QST, vol. 32, pp. 36-43; June, 1948.
? David G. C. Luck, "Properties of some wide-band phase splitting networks," Proc. I.R.E., vol. 37, pp. 147-151; February, 1949.
? Some of the networks obtained as a result of this investigation form the subject of British Patent Application No. 16698/49.
? 這個假設不失一般性，因為唯一其他可能的選擇是? 在?。然而，在這種情況下，我們將有? 在?，然后我們可以將以下討論的結果應用于?，它逼近1就像? 一樣。
? A. Cayley, "Elliptic Functions," 2nd ed., George Bell & Sons, London; 1895.
? K. Hayashi, "Tafeln der Besselschen, Theta, Kugel-undanderer Funktionen," Berlin; 1930.
? L. M. Milne-Thomson, "Die elliptischen Funktionen von Jacobi," Julius Springer, Berlin; 1931.
? 值得注意的是，在濾波器設計的情況下，必須使用從模數? 到較小模數? 的“第一變換”。盡管這種變換在許多方面與我們問題中使用的變換相似，但它與由式（10a）和（10b）定義的變換不同，因為它僅對奇數? 值導致? 的有理函數。對于偶數? 值，為了使? 成為? 的有理函數，如 Darlington 所示，必須通過? 和? 之間更復雜的關系來定義?（請參見腳注 27 中的參考文獻）。
? O. J. Zobel, "Distortion correction in electrical circuits with constant resistance recurrent networks," Bell Sys. Tech. Jour., vol. 7, pp. 438-534; July, 1928.
? W. Saraga, "Attenuation and phase shift equalisers," Wireless Eng., vol. 20, pp. 163-181; April, 1943.
? R. F. Baum, "A contribution to the approximation problem," Proc. I.R.E., vol. 36, pp. 863-869; July, 1948.
? T. Laurent, "New principles for practical computation of filter attenuation by means of frequency transformation," Ericsson Technics, vol. 3, pp. 57-72; 1939.
? E. Rumpelt, "Schablonenverfahren fuer den Entwurf elektrischer Wellenfilter auf der Grundlage der Wellenparameter," Telegraphen Fernsprech. Funk und Fernsch-und Technik, vol. 31, pp. 203210; August, 1942.
? F. Scowen, "Electric Wave Filters," Chapman & Hall Ltd., London, pp. 72-74; 1945. ?
? F. Pyrah, "Constant impedance equalisers: Simplified method of design and standardisation," British P.O. Elec. Eng.'s Jour., vol. 92, pp. 204-211; October, 1939.
? D. N. Truscott, "Logarithmic charts and circuit performance," Electronic Eng., vol. 14, pp. 745-748; May, 1942.
? S. Darlington, "Synthesis of reactance 4-poles which produce prescribed insertion loss characteristics," Jour. Math. Phys., vol. 13, pp. 257-353; September, 1939.
? 在相移網絡的這種分解的一般情況下，得到的各個? 值不一定是實數，而可能以共軛復數對出現。然后，兩個相應的基本部分可以合并為一個物理部分，其標準化的串聯臂電抗為?，其中?。然而，對于相位分割網絡，在使用泰勒或切比雪夫逼近法進行性能曲線時，不會出現復數? 值，而且在其他好的逼近中似乎也不會出現。另一方面，在濾波器設計中，它們的出現是規定的。
? W. A. Marrison, United States Patent No.?, dated September 12, 1933.
? W. Saraga, British Patent No. 594,431, dated May 29, 1945, and U.S. Patent Application No. 670,264.
? E. K. Sandeman, "Phase compensation," Elec. Commun., vol. 7, pp. 309-315; April, 1929.
? M. Wald, "Eine Kunstschaltung zur Verdreifachung des Winkelmasses eines Kreuzgliedes und ihre Anwendung zum Phasenausgleich in Pupinleitungen," Elekt. Nach. vol. 19, pp. 196-199; October, 1942. ?
? A. T. Starr, British Patent No. 342,407, dated October 30, 1929.
? H. W. Bode, "Network Analysis and Feedback Amplifier Design," D. Van Nostrand Company, Inc., New York, N. Y., pp. 216-218; 1945.
? C. H. Dagnall and P. W. Rounds, "Delay equalization of eightkilocycle carrier programme circuits," Bell Sys. Tech. Jour., vol. 23, pp. 181-195; April, 1949.
? F. S. Farkas, F. J. Hallenbeck, and F. E. Stehlick, "Band pass filter, band elimination filter and phase simulating network for carrier programme systems," Bell Sys. Tech. Jour., vol. 28, pp. 196220; April, 1949.
? J. B. S. Haldane, "On the non-linear difference equation?," Proc. Cambridge Phil. Soc., vol. 28, part II, pp. 234243 ; 1932.
? L. Silberstein, "Construction of groups of commutative functions," Phil. Mag., pp. 43-54; January, 1945.
? J. Hadamard, "Two works on iteration and related questions," Bull. Amer. Math. Soc., vol. 50, pp. 67-75; February, 1944.
? G. Boole, "A Treatise on the Calculus of Finite Differences," Macmillan and Co., London, 3rd Ed., p. 17; 1880.

https://120years.net/saraga-generatorwolja-saragagermany1931/

審核編輯：黃飛

?