零極點(diǎn)的理解是模擬電路最關(guān)鍵的基礎(chǔ)之一，信號(hào)與系統(tǒng)都會(huì)講自然響應(yīng)，自然響應(yīng)就是偏微分方程的通解部分，而受迫響應(yīng)則是偏微分方程的特解。本文將詳解零極點(diǎn)與頻率響應(yīng)之間的關(guān)系。

我們從頻率域來(lái)分析零極點(diǎn)的影響。從頻率域上，零點(diǎn)和極點(diǎn)會(huì)決定系統(tǒng)的頻率響應(yīng)。我們令系統(tǒng)傳輸函數(shù)H（s）中s（=σ+jω） 的實(shí)部σ=0而虛部ω仍然是變量，就得到了頻率響應(yīng)函數(shù)H（jω）。頻率響應(yīng)函數(shù)代表系統(tǒng)在恒包絡(luò)正弦小信號(hào)輸入時(shí)，輸出正弦信號(hào)相對(duì)輸入正弦信號(hào)的幅度和相位變化。頻率響應(yīng)函數(shù)可以表示為：

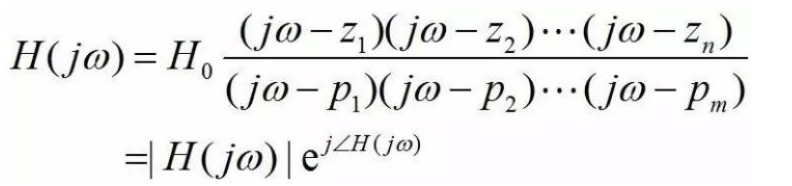
頻率響應(yīng)H（jω）是復(fù)數(shù)。其幅度|H（jω）|代表當(dāng)正弦信號(hào)頻率為ω時(shí)，輸出正弦信號(hào)幅度相對(duì)輸入正弦信號(hào)幅度的比值（即系統(tǒng)的增益），而其相位∠H（jω）則代表輸出正弦信號(hào)相對(duì)輸入正弦信號(hào)的相位變化。根據(jù)高中數(shù)學(xué)，頻率響應(yīng)的幅度和相位可以表示為各個(gè)零點(diǎn)/極點(diǎn)的貢獻(xiàn)：

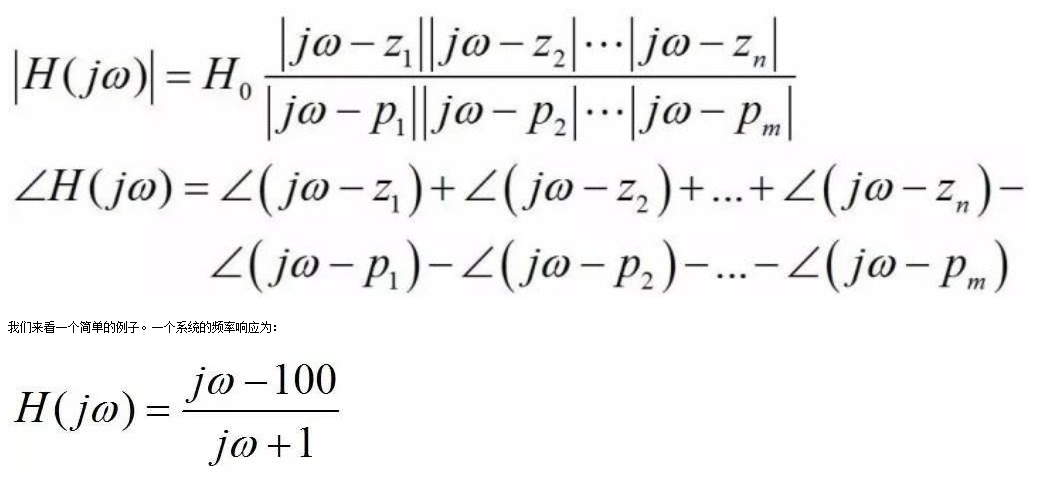
它有一個(gè)極點(diǎn)（實(shí)部σ=-1，虛部ω=0，其模為1）和一個(gè)零點(diǎn)（實(shí)部σ=100，虛部ω=0，其模為100）。由于極點(diǎn)的實(shí)部小于0，該系統(tǒng)是穩(wěn)定的。當(dāng)ω=0的時(shí)候［即DC（直流）響應(yīng)］，分母的模為1，相位為0，分子的模為100，相位為π，因此頻率響應(yīng)的幅度為100，相位為π。我們接下來(lái)增加一點(diǎn)點(diǎn)ω，讓它等于0.001。這個(gè)時(shí)候ω遠(yuǎn)遠(yuǎn)小于極點(diǎn)的模，因此頻率響應(yīng)分母的值和DC時(shí)沒(méi)有顯著區(qū)別（1+j0.001≈1）。ω也遠(yuǎn)遠(yuǎn)小于零點(diǎn)的模，因此頻率響應(yīng)分子的值也和DC時(shí)基本相同。所以當(dāng)ω的值遠(yuǎn)遠(yuǎn)小于某個(gè)極點(diǎn)/零點(diǎn)的模的時(shí)候，該極點(diǎn)/零點(diǎn)的效應(yīng)可以忽略不計(jì)。這也是在實(shí)際電路設(shè)計(jì)中很多頻率遠(yuǎn)高于電路工作頻率的極點(diǎn)/零點(diǎn)在分析的時(shí)候可以忽略的原因。當(dāng)ω增加至1時(shí)，分母變?yōu)椋╦1+1），此時(shí)分母的幅度由DC時(shí)的1變?yōu)椤?，相位則由0變?yōu)棣?4。由于ω仍然遠(yuǎn)小于零點(diǎn)（1《《100），分子較DC相比仍然沒(méi)有變化。頻率ω=1時(shí)對(duì)極點(diǎn)是一個(gè)轉(zhuǎn)折點(diǎn)：隨著ω繼續(xù)增長(zhǎng)，該極點(diǎn)的效應(yīng)漸漸變得顯著。當(dāng)ω=10的時(shí)候，ω已經(jīng)遠(yuǎn)遠(yuǎn)大于極點(diǎn)的模，因此頻率響應(yīng)的分母可以近似為jω，相位為π/2。此后隨著ω繼續(xù)增長(zhǎng)，分母的模隨之變大，因此在零點(diǎn)發(fā)揮作用前，頻率響應(yīng)的幅度會(huì)隨著頻率增大以20dB/dec的速度減小。另一方面，當(dāng)ω增大到遠(yuǎn)大于零點(diǎn)的模（》》100）時(shí)，頻率響應(yīng)的分子可以近似為jω，因此分子的相位為π/2，且分子的模隨著頻率增長(zhǎng)以20dB/dec的速度增長(zhǎng)。此時(shí)分子和分母的模都以20dB/dec增長(zhǎng)，因此互相抵消，頻率響應(yīng)的幅度不再變化，而相位則由DC時(shí)的π變?yōu)?。

H（jω）的幅度和相位

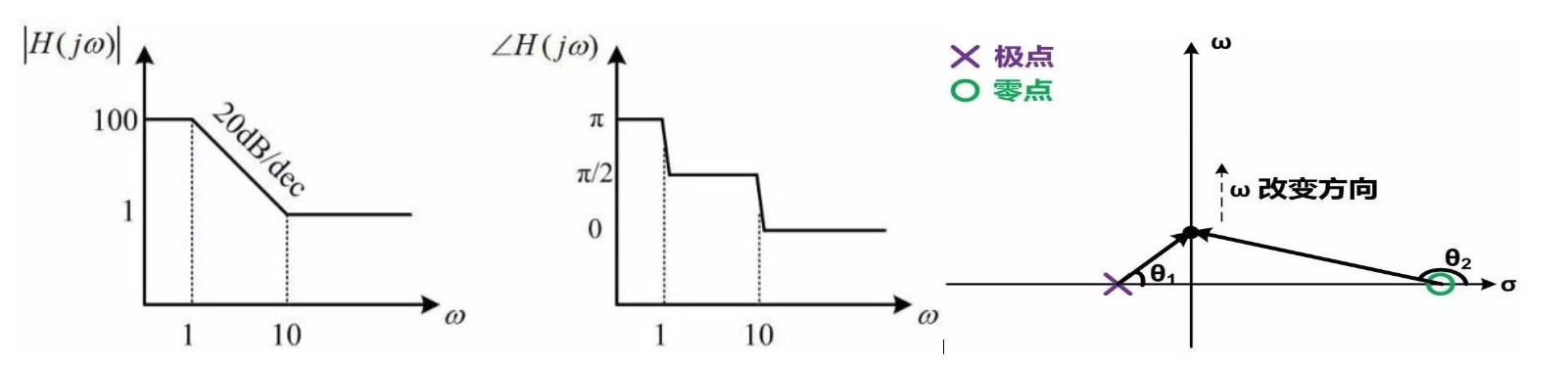
零點(diǎn)和極點(diǎn)對(duì)頻率響應(yīng)的效果也可以由s平面零極點(diǎn)圖解釋。上面例子的零極點(diǎn)圖如下：

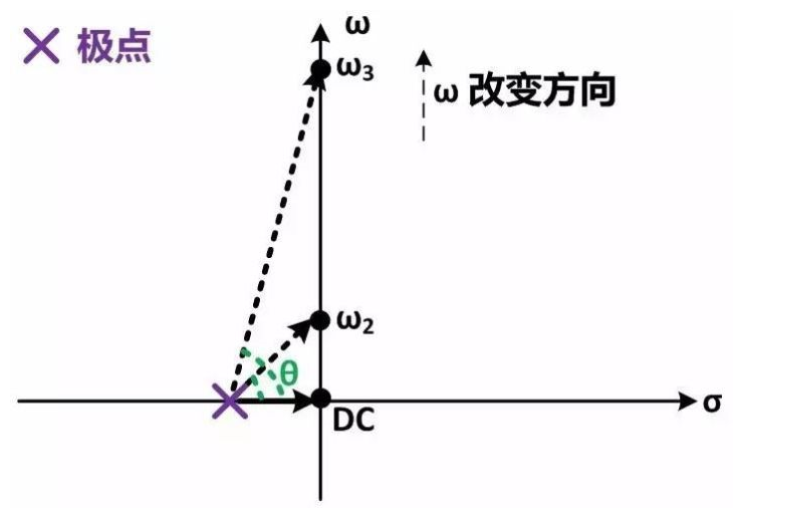
開(kāi)始ω1=0 （即DC響應(yīng)），極點(diǎn)向量的相位為0。之后隨著ω增加，極點(diǎn)向量的長(zhǎng)度逐漸增長(zhǎng)，相位貢獻(xiàn)θ也逐漸變大。當(dāng)ω等于極點(diǎn)的模的時(shí)候（ω2），根據(jù)初中數(shù)學(xué)極點(diǎn)向量的長(zhǎng)度變?yōu)镈C時(shí)的√2倍，而相位角θ為π/4。之后隨著ω繼續(xù)增長(zhǎng)到遠(yuǎn)大于極點(diǎn)的模的時(shí)候，極點(diǎn)向量漸漸變得和ω軸平行，此時(shí)極點(diǎn)向量的長(zhǎng)度近似等于ω，而相位角θ也漸漸逼近π/2。對(duì)于零點(diǎn)也可以做類(lèi)似的分析。這樣圖解分析與之前分析的結(jié)果相同，但是更直觀。

零點(diǎn)和極點(diǎn)對(duì)頻率響應(yīng)的影響可以總結(jié)為：

*當(dāng)頻率遠(yuǎn)小于某零點(diǎn)/極點(diǎn)的模時(shí)，該零點(diǎn)/極點(diǎn)對(duì)頻率響應(yīng)的影響可以忽略。

*當(dāng)頻率接近某極點(diǎn)的模時(shí)，該極點(diǎn)的效果漸漸體現(xiàn)。當(dāng)頻率遠(yuǎn)大于該極點(diǎn)時(shí)，該極點(diǎn)使得頻率響應(yīng)的幅度以20dB/dec的速度衰減，而相位相對(duì)DC產(chǎn)生-π/2的變化。

*共軛極點(diǎn)是一種特殊的極點(diǎn)，它們總是成對(duì)出現(xiàn)且共軛極點(diǎn)對(duì)的模都相等，因此當(dāng)頻率遠(yuǎn)大于一對(duì)共軛極點(diǎn)的模的時(shí)候，該共軛極點(diǎn)對(duì)會(huì)使頻率響應(yīng)的幅度以40dB/dec的速度衰減，而相位相對(duì)DC產(chǎn)生-π的變化。而在頻率接近共軛極點(diǎn)對(duì)的模的時(shí)候，頻率響應(yīng)曲線的變化取決于共軛極點(diǎn)對(duì)的位置（詳見(jiàn)下文）。

*當(dāng)頻率接近某零點(diǎn)的模時(shí)，該零點(diǎn)的效果漸漸體現(xiàn)。當(dāng)頻率遠(yuǎn)大于該零點(diǎn)時(shí)，該零點(diǎn)使得頻率響應(yīng)的幅度以20dB/dec的速度增加。而相位相對(duì)DC產(chǎn)生π/2（當(dāng)零點(diǎn)在左半平面）或-π/2（當(dāng)零點(diǎn)在右半平面）的變化。

*頻率響應(yīng)的總體幅度/相位取決于所有零點(diǎn)和極點(diǎn)對(duì)幅度/相位的貢獻(xiàn)。

共軛極點(diǎn)對(duì)

共軛極點(diǎn)對(duì)是一類(lèi)特殊的極點(diǎn)。一對(duì)共軛極點(diǎn)（s-p）（s-p*）可以寫(xiě)作

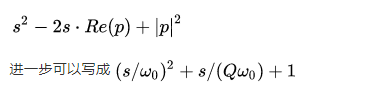其中ω0為共軛極點(diǎn)的諧振頻率，Q稱(chēng)作共軛極點(diǎn)的品質(zhì)因數(shù)。

共軛極點(diǎn)對(duì)模型最初來(lái)源于LC諧振電路，如下圖中的RLC串聯(lián)電路。

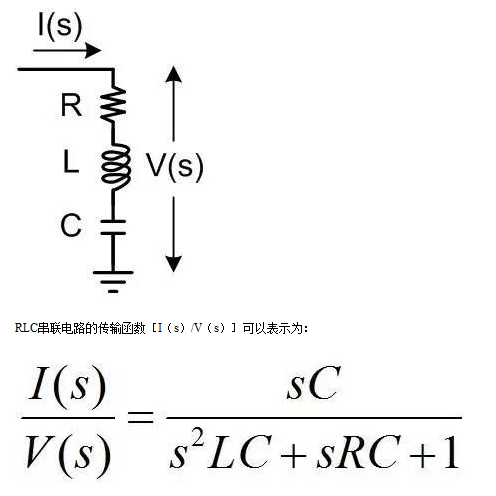
其中共軛極點(diǎn)的諧振頻率ω0=1/√LC即LC tank的諧振頻率，品質(zhì)因數(shù)Q=（1/R）?√（L/C）即為L(zhǎng)C tank的品質(zhì)因數(shù)，表示在諧振頻率附近每周期LC tank存儲(chǔ)的能量與耗散能量的比值。共軛極點(diǎn)可以由LC tank形成，也可由反饋通路形成。

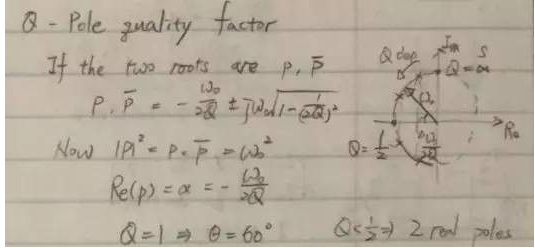
共軛極點(diǎn)對(duì)的Q值由共軛極點(diǎn)的位置決定。當(dāng)共軛極點(diǎn)的諧振頻率固定而改變品質(zhì)因數(shù)（即固定L和C而改變R）時(shí)，共軛極點(diǎn)對(duì)的軌跡在以原點(diǎn)為圓心，半徑為ω0的圓上。當(dāng)共軛極點(diǎn)對(duì)靠近縱軸時(shí)，品質(zhì)因數(shù)變大；而當(dāng)共軛極點(diǎn)對(duì)靠近橫軸時(shí)，品質(zhì)因數(shù)變小。共軛極點(diǎn)對(duì)的品質(zhì)因數(shù)必須大于等于1/2，當(dāng)Q小于1/2時(shí)共軛極點(diǎn)對(duì)退化為兩個(gè)實(shí)極點(diǎn)。

對(duì)于傳輸函數(shù)具有共軛極點(diǎn)對(duì)的系統(tǒng)，系統(tǒng)的自然響應(yīng)中含有包絡(luò)指數(shù)衰減的正弦波。有時(shí)候在放大器的瞬時(shí)響應(yīng)中會(huì)看到衰減震蕩的現(xiàn)象，這種現(xiàn)象就是由共軛極點(diǎn)造成的。

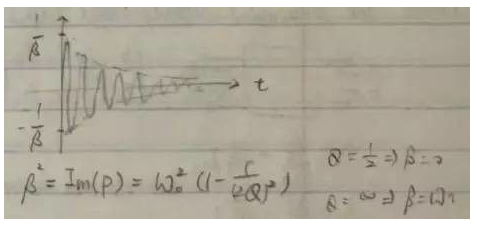
正弦波的頻率接近諧振頻率ω0，而包絡(luò)的衰減速度取決于Q。Q值約等于包絡(luò)衰減到初始值的1/e時(shí)所需要的諧振周期。Q值大時(shí)包絡(luò)衰減較慢，反之Q值小時(shí)包絡(luò)衰減較快。在放大器設(shè)計(jì)中我們往往希望看到settling time比較小的瞬時(shí)響應(yīng)，因此應(yīng)該避免高Q值得共軛極點(diǎn)對(duì)。

共軛極點(diǎn)對(duì)另一個(gè)重要性質(zhì)是它會(huì)引起頻率響應(yīng)的尖峰（peaking）。這一點(diǎn)可以從零極點(diǎn)圖來(lái)理解。

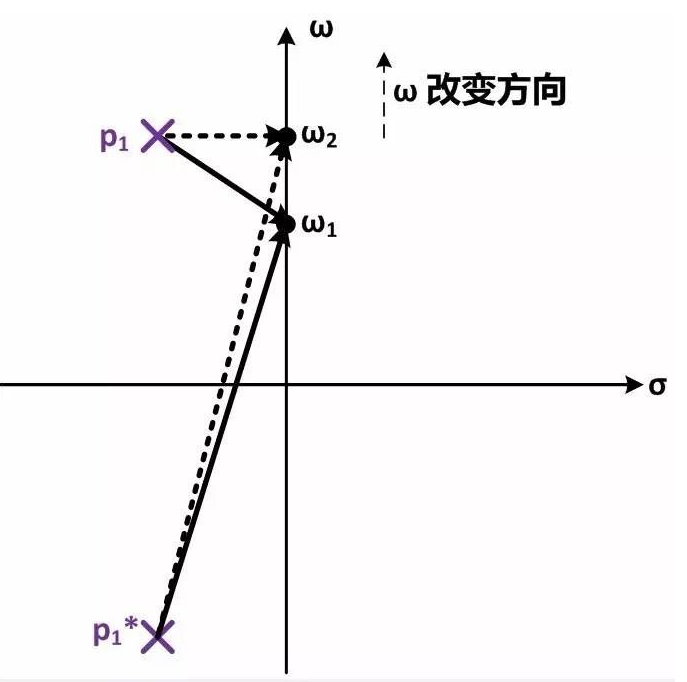
在零極點(diǎn)圖上，有共軛極點(diǎn)p1和p1*，位置在σ±jω0。當(dāng)頻率從ω1（略小于ω0）移動(dòng)到ω2（等于ω0）時(shí)，連接到極點(diǎn)p1*的極點(diǎn)向量長(zhǎng)度基本不變，但連接到極點(diǎn)p1的極點(diǎn)長(zhǎng)度顯著變短了。因此頻率響應(yīng)在諧振頻率（ω=ω0）處會(huì)產(chǎn)生一個(gè)尖峰，尖峰的高度隨Q值變大而變大。極端情況是Q值無(wú)窮大時(shí)，此時(shí)p1和p1*都在ω軸上，因此當(dāng)ω=ω0時(shí)，連接p1和ω的極點(diǎn)向量長(zhǎng)度為0，這樣頻率響應(yīng)的幅度變?yōu)闊o(wú)窮大，所以就產(chǎn)生了高度無(wú)窮大的尖峰。在設(shè)計(jì)需要較小settling time的放大器時(shí)我們希望避免明顯的頻率響應(yīng)尖峰（頻率響應(yīng)尖峰明顯=》共軛極點(diǎn)對(duì)Q值大=》瞬時(shí)響應(yīng)中衰減震蕩持續(xù)時(shí)間較長(zhǎng)=》settling time較長(zhǎng)）；但另一方面在設(shè)計(jì)寬帶放大器（例如在CML電路中）時(shí)我們往往會(huì)故意引入頻率響應(yīng)尖峰以增加帶寬。

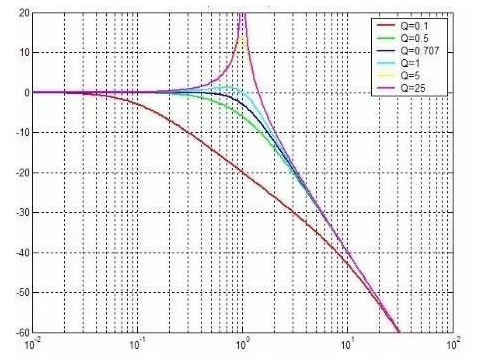
頻率響應(yīng)尖峰與Q值的關(guān)系

至此我們回顧了EE215A所需要的電路分析基礎(chǔ)知識(shí)。接下來(lái)我們將應(yīng)用它們?nèi)シ治鼍唧w電路。

下面我們有請(qǐng)助教哥給大家?guī)?lái)傳輸函數(shù)標(biāo)準(zhǔn)型的補(bǔ)充。

將傳輸函數(shù)寫(xiě)成標(biāo)準(zhǔn)形式有助于我們迅速畫(huà)出頻率響應(yīng)的草圖，這對(duì)我們今后分析放大器、鎖相環(huán)的噪音和穩(wěn)定性至關(guān)重要。

一階零極點(diǎn)

之前說(shuō)的零極點(diǎn)是標(biāo)準(zhǔn)的零極點(diǎn)定義，也可以稱(chēng)為正向零極點(diǎn)。注意我們要把極點(diǎn) ，零點(diǎn)寫(xiě)成歸一化的形式，便于我們將基準(zhǔn)增益拆分出來(lái)。在下圖中，基準(zhǔn)增益都是A0

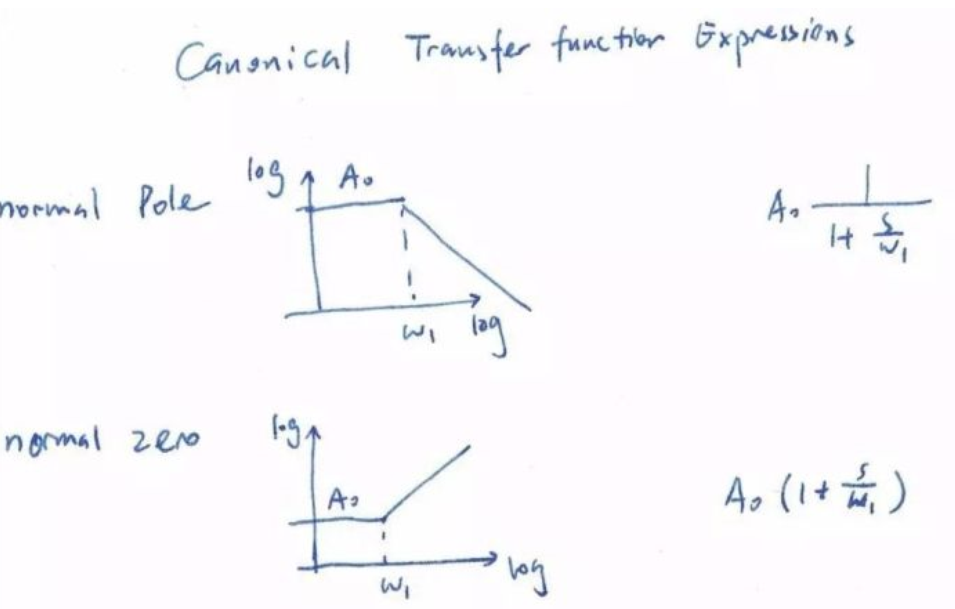
逆向極點(diǎn)和逆向零點(diǎn)是新引入的概念。逆向極點(diǎn)的意思是如果從無(wú)窮高頻率出發(fā)向DC 移動(dòng)，頻率響應(yīng)會(huì)遇到一個(gè)-1斜率滾降（或者叫-20dB/dec如果用分貝）。同理，逆向零點(diǎn)是從無(wú)窮高頻率出發(fā)向DC 移動(dòng)，頻率響應(yīng)會(huì)遇到一個(gè)+1斜率上升（或者叫-20dB/dec如果用分貝）。逆向極點(diǎn)是由一個(gè)在原點(diǎn)的零點(diǎn)和一個(gè)在ω1的極點(diǎn)組成。逆向零點(diǎn)由一個(gè)在原點(diǎn)的極點(diǎn)和一個(gè)在ω1的零點(diǎn)組成。如果我們將傳輸函數(shù)寫(xiě)成如下的逆向形式而不是一般的正向形式，頻率響應(yīng)就能很快被畫(huà)出來(lái)。

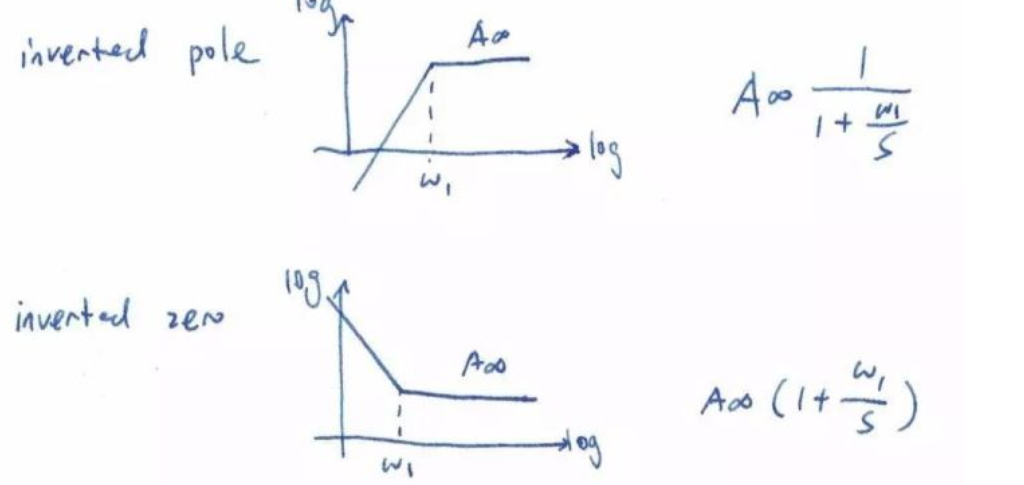
正向、逆向極點(diǎn)和零點(diǎn)的相位響應(yīng)曲線大家可以很容易想出來(lái)，只要注意頻率變化方向即可，所以就不重復(fù)講了。

靈活運(yùn)正向、逆向零極點(diǎn)對(duì)于分析這對(duì)我們今后分析放大器、PLL的噪音和穩(wěn)定性至關(guān)重要。下面舉個(gè)例子：

二階零極點(diǎn)

我們先重新學(xué)習(xí)二次函數(shù)的根的表達(dá)式。我們?cè)诟咧袑W(xué)的二次函數(shù)根長(zhǎng)這樣：

但是問(wèn)題是，這樣的表達(dá)式是高熵的，比如某一個(gè)傳輸函數(shù)的分母的根按照傳統(tǒng)高中學(xué)過(guò)的表達(dá)式，長(zhǎng)這樣：

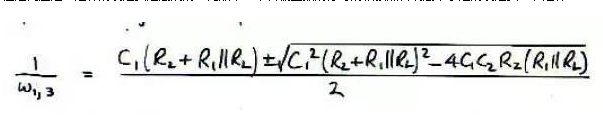
你看這個(gè)表達(dá)式，長(zhǎng)得這么丑，看著就渾身難受。除非你用一個(gè)繪圖軟件，并把所有R C的值帶入，否則你沒(méi)有辦法快速找出這兩個(gè)根的關(guān)系，沒(méi)法根據(jù)這個(gè)表達(dá)式快速繪出頻率響應(yīng)。更重要的是，你沒(méi)有辦法從這個(gè)表達(dá)式快速看出要怎樣設(shè)計(jì)R C以達(dá)到你的目的。

所以Prof. Abidi（原引Prof. Middlebrook）教育我們要用適合電路設(shè)計(jì)的二次函數(shù)根式。

回去看高中根式，其實(shí)這個(gè)根式用的是兩根之和等于-b/a 的性質(zhì)。但是二次函數(shù)兩根之積還等于c/a，新根式正是運(yùn)用了兩根之積性質(zhì)。換句話說(shuō)，高中公式看的是兩根的算術(shù)平均，新根式看的是兩個(gè)的幾何平均。不要忘了在對(duì)數(shù)刻度中，幾何平均比算術(shù)平均更加有意義，因?yàn)閮蓚€(gè)刻度的中點(diǎn)是幾何平均。

新根式如下：

注意看新根式的對(duì)稱(chēng)性！拿到一個(gè)二階表達(dá)式，我們只要算Q和ω0就可以了。有同學(xué)會(huì)問(wèn)，那F怎么辦，F(xiàn)不是還是亂糟糟么？其實(shí)不然，我們把F和Q的關(guān)系畫(huà)一下：

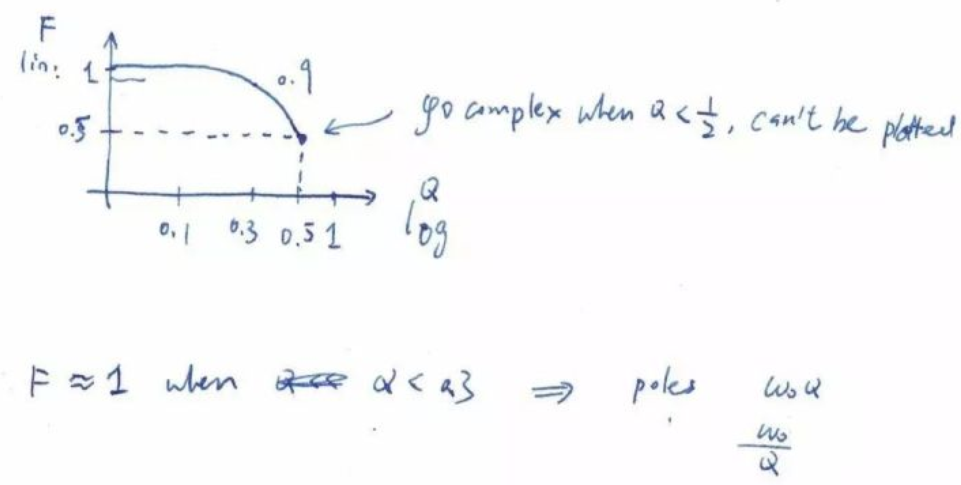
你看，當(dāng)Q小于0.3的時(shí)候，F(xiàn)約等于1。所以我們只要根據(jù)Q的表達(dá)式，估計(jì)Q值，如果遠(yuǎn)小于0.3，那么就是兩個(gè)實(shí)根，一個(gè)是-ω0Q，另一個(gè)-ω0/Q 啦！

有同學(xué)會(huì)問(wèn)，那Q 在0.3和0.5中間時(shí)候怎么辦呢？很簡(jiǎn)單，把他們近似成兩個(gè)重實(shí)根就好了。

如果Q大于0.5，我們就有復(fù)數(shù)根（共振）了。

這樣的表達(dá)式利于具體的電路設(shè)計(jì)。我們可以分析電路模型，把ω0和Q用電路元件的參數(shù)表達(dá)出來(lái)。之后比如我們可以設(shè)計(jì) ω0以達(dá)到帶寬要求。設(shè)計(jì)Q 以達(dá)到穩(wěn)定性要求。

二階帶通

二階帶通標(biāo)準(zhǔn)形式如下，零級(jí)點(diǎn)圖中畫(huà)的是極點(diǎn)的軌跡（隨Q變化而移動(dòng)）。

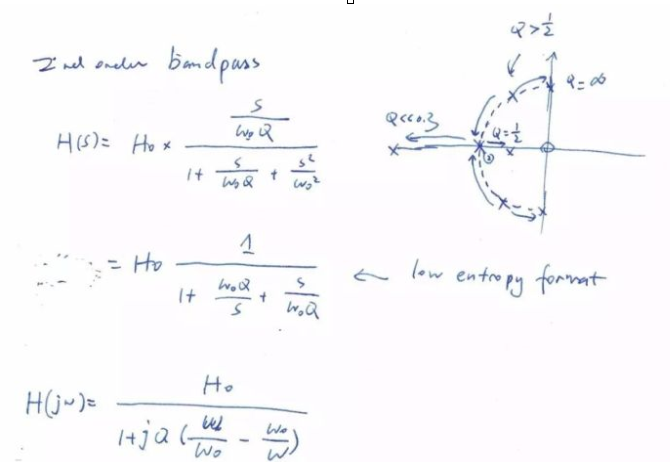
通過(guò)新根式，我們可以畫(huà)出幅度頻率響應(yīng)

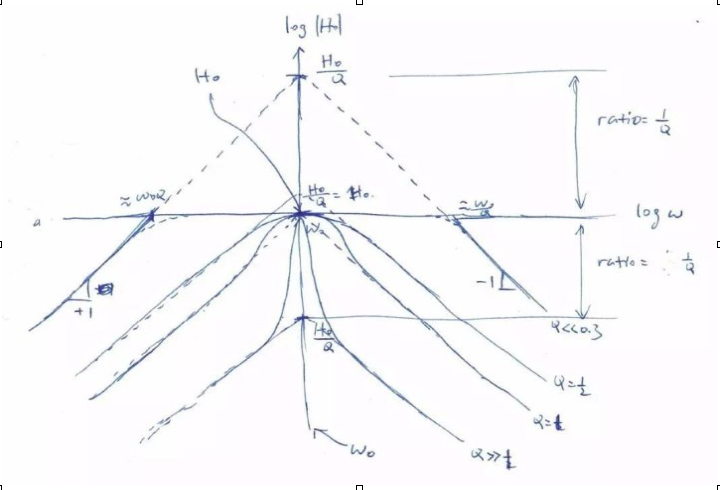
縱軸時(shí)|H| 對(duì)數(shù)刻度，橫軸是ω對(duì)數(shù)刻度。

中間交匯處是H0，ω0。不管Q為何值，幅度響應(yīng)都在ω0通過(guò)H0。

當(dāng)Q小于0.3時(shí)，雙實(shí)根距離很遠(yuǎn)，我們有一個(gè)正向極點(diǎn)和一個(gè)逆向極點(diǎn)。

當(dāng)Q等于1時(shí)，兩個(gè)漸近線的延長(zhǎng)線正好交匯于H0，實(shí)際響應(yīng)有一個(gè)小尖峰。

當(dāng)Q遠(yuǎn)大于1時(shí)，兩個(gè)漸近線交匯于H0/Q 很低的一個(gè)點(diǎn)，但是|H|還是要過(guò)H0，所以有一個(gè)很大尖峰。

相位響應(yīng)（近似漸近線）如下：

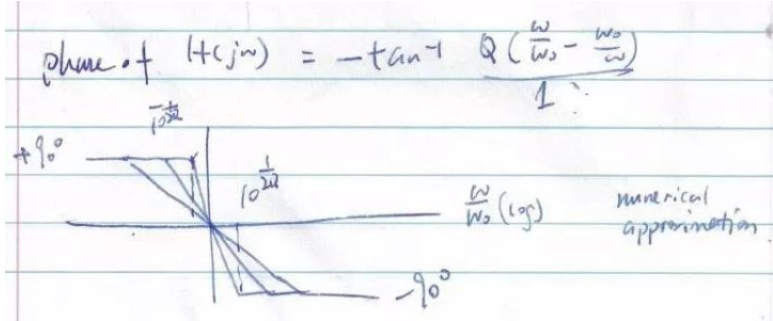
隨著Q增大，角度變化越快。

二階低通與二階帶通類(lèi)似，只是少了一個(gè)零點(diǎn)

標(biāo)準(zhǔn)表達(dá)式如下

幅度響應(yīng)如下

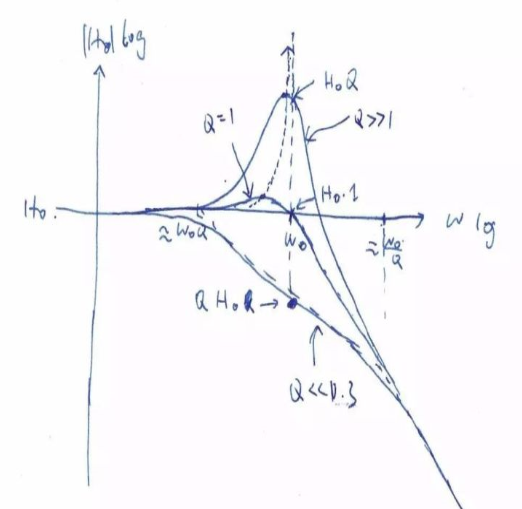
記住幅度響應(yīng)在ω0時(shí)為H0Q，所以當(dāng)Q=1時(shí)幅度在ω0時(shí)為H0。但這時(shí)我們已經(jīng)有微小的尖峰了。

注意幅度的最高點(diǎn)永遠(yuǎn)小于ω0，當(dāng)Q增大時(shí)，無(wú)限接近于ω0。

二階低通相位響應(yīng)與帶通的類(lèi)似，只是整體向下移動(dòng)90°。

同樣地，我們可以定義正向二階極點(diǎn) 零點(diǎn)和反向二階零極點(diǎn)，大家到此應(yīng)該可以想出以下推論了。