我們為 V SYSTEMS 區塊鏈平臺設計了了一個注重高擴展性的權益證明（PoS）共識機制，稱為超級節點權益證明共識（Supernode PoS）。該共識機制的特點包括固定的區塊鑄幣間隔、冷鑄幣、以及權益流動性。

1. 能源的作用

早在 2011 年，比特幣網絡經歷了可能是它的第一次顯著增長。那時，絕大部分的比特幣使用者及支持者們對于這一去中心化？網絡的能源消耗問題可能并不關心。然而，Peercoin 項目已經提出了問題：能源消耗對達成共識真的必不可少嗎？對于大多數比特幣的鼓吹者而言，這個問題的答案是肯定的：比特幣就像是黃金；挖金礦所消耗的能源給黃金賦予了價值，而比特幣挖礦所消耗的能源不僅能使網絡達成共識并保共識安全，也是比特幣貨幣價值的支撐。

但回顧歷史，人們對于是什么給予了黃金貨幣價值這一問題眾說不一。奧地利學派推斷其必然來自于某種初始的商品價值。有人推測，一旦民族國家有了足夠的能力可以剝奪黃金的貨幣角色，那么黃金就應該沒有什么價值了。只要人們相信比特幣的貨幣效用，就自然會問道：到底是什么給予了比特幣價值？

Peercoin 在一定意義上是在嘗試解開這個最重要的貨幣奧秘。它成功地將工作量證明或（借用黃金挖礦而來的）挖礦的能源消耗從共識算法中分離了出來，并將能源的作用限制到僅用于數字貨幣的發行。接下來很容易考查能源僅剩的與貨幣發行的關聯，因為人們可以切換到某種類似股票的發行模型，從而可輕易將能源成分從發行機制中剔除。

因而事實上，權益證明共識技術進一步表明了貨幣價值并非來源于能源消耗。而且，貨幣價值也不需要內在價值或任何其他類型的商品價值。僅由貨幣效用就可以賦予價值。

2. 權益證明共識—無能耗的共識

Peercoin 達成共識的方法極具開創性。它完全拋棄了比特幣的取得驚人成功的工作量量證明共識機制，而去尋求一種完全不不依賴能源消耗的算法。它對權益證明充滿信心，相信這一概念可以獨立地形成一個共識算法，而不需要任何工作量量證明成分。

有的作者誤解這一點。就共識算法而言， Peercoin 是純權益證明的。工作量量證明僅僅用于數字貨幣的公平分配，并不不參與共識算法。

對于一個無能耗的共識系統，我們稱產生區塊的過程為鑄幣（minting），以區分于消耗大量量能源的挖礦過程。

Peercoin 的共識算法繼承了了比特幣的一些特征。例如，它也隨機地產生區塊，僅可以觀察到平均區塊間隔或目標區塊間隔。與這一過程相關聯的是一個稱作權益證明難度的度量，對應于該度量量有一個？用于鑄幣的由共識協議維護的可調節閥值。

引入權益證明共識機制是區塊鏈技術發展中的一個巨大里程。它不僅消除了為達到分布式共識？而進行挖礦的能源消耗，也極大增強了區塊鏈的擴展能力，為區塊鏈技術的各種應用鋪平了道路。

3. 針對權益證明共識的批評

自從 Peercoin 開創性的面世后，常有人針對該系統某些方面提出批評。一個經常能聽到的批評是“權益欺壓（stake grinding）”。這種攻擊在 2012 年Peercoin 最初版本發布后不久即被發現。Peercoin 于 2013 年2 月發布的 0.3 版本中實現了一個重要的新算法，以抵抗這種類型的攻擊。

這個新算法引入了一個稱為“核（kernel）”的共識字段。它是一個會隨區塊鏈逐漸變化共識數字：在給定的時間隔內協議會選中一個區塊，被選中的區塊可以改變核的一個比特位。核可以看成是區塊鏈上的一個緩慢改變的隨機源（entropy source），區塊鏈的一個短分叉給它帶來的影響將十分有限。有了核的保護，權益欺壓的威脅就基本上被消除了。

另一個針對權益證明共識常見的批評為“無風險分叉（nothing-at-stake）”問題。該問題可表述為，由于鑄幣不涉及工作量或能源消耗，鑄幣者可嘗試在區塊樹的所有分支上進行鑄幣而不會有任何損失。因而在利益的驅使下，鑄幣者將會在所有分支上進行鑄幣，以避免某一給定分叉輸掉競爭而導致的損失。這種論證的問題在于它忽略了權益證明的核心原則。權益證明的思想是，當某人在貨幣供應中擁有了的一定比例的權益后，他應當已有激勵去做對整個系統有益的事情，而不會對系統進行攻擊。由于在所有分支上進行鑄幣可認為是對協議的一種攻擊，它已經是權益證明所不允許的了。按這樣的觀點，即便是所謂的理性鑄幣者也不應當以內部貨幣單位來估量價值，而應當以外部穩定貨幣來衡量其權益的總價值。

考慮到對權益價值可能的負面影響，這或許與公地的悲劇有一定關聯。然而，即便按公地悲劇最初的解釋，可能避免的少量鑄幣損失也比不上權益價值潛在損失的量級。事實上，沒有證據表明“無風險分叉”導致了任何為進一步制止該攻擊而作出的協議調整。

4. 關于冷鑄幣的爭論

在權益證明共識面世后不久，Peercoin 社區就掀起了了關于冷鑄幣（cold minting）特征的討論。它與比特幣稱為冷存儲的特征有關，即私鑰由離線錢包進行管理理。由于權益證明共識要求鑄幣者對區塊進行簽名，為此其私鑰必須保持在線。這與冷存儲可獲得的高安全性是矛盾的。

解決的辦法是將鑄幣與消費的角色相分離。也就是說，權益所有權的密鑰與鑄幣所需的密鑰可以是不同的。那么，鑄幣密鑰保持在線的同時，所有權密鑰可以放置在離線存儲中。這自然就會允許出現鑄幣池（minting pool），類似于比特幣的礦池。鑒于比特幣礦池的中心化傾向，鑄幣池也是不被贊成。

考慮到眾多因素，冷鑄幣特征并未在 Peercoin 中實現。而在其他一些權益證明系統中確已經實現了鑄幣密鑰與所有權密鑰的分離。這種分離現在通常被稱為權益代理或出租。

5. 向超級節點的轉換

區塊鏈行業在最近幾年年中見證了去中心化應用的巨幅增長。比特幣與以太坊都出現過周期性交易擁堵。越來越多的關注點投向了單一區塊鏈的表現上。

這就已經為共識算法的設計帶來了幾個問題。首先，挖礦或鑄幣節點可能沒有足夠的激勵升級節點硬件。且這種節點也可能大量存在。由于整個網絡的維護成本非常之大，有的節點在硬件升級上注定會被甩在后面。

另一個問題與比特幣產生區塊的隨機過程有關。盡管平均區塊間隔是 10 分鐘，但有時候下一個區塊的產生需要等待比這長得多的時間。對于面向性能的系統而言，這就成了一個問題。這類系統更傾向于固定的而非隨機分布的響應時間。

如上的考慮，鑄幣協議應當設計成有固定的區塊間隔，且要將鑄幣節點提升到比網絡中其他節點更重要的位置。

6. 鑄幣時段與鑄幣權競爭

為實現鑄幣的固定區塊間隔，我們定義一個稱為鑄幣時段（minting slot）的實體。每個時段對應于鑄幣權的一次平均分配。因此，為獲得某個時段的鑄幣權，一個潛在的鑄幣參與者必須取得該時段的所有權。

在每分鐘內定義了60 個鑄幣時段，每個時段對應于其中特定的一秒鐘。要在給定的一秒鐘內取得鑄幣權，必須取得該秒對應鑄幣時段的所有權。

基本上系統中的鑄幣者將會輪流著進行鑄幣。這樣做的好處是，如果有某些超級節點停？止了鑄幣，不管出于什么原因，他們對系統響應及吞吐量的影響都會被最小化。

每個超級節點的本地時鐘都通過網絡時間協議進行同步，以保證鑄幣活動的正常順序。回到 2009 年年，比特幣選擇不依賴于網絡時間協議進行時鐘同步，所以比特幣協議允許礦工們時鐘偏移多達 2 個小時。通常而言，現今的網絡時間協議可以作為一項基本的互聯網服務，與域名服務類似，因而可以合理地假設其有很高的安全性。

鑄幣時段的競爭可以允許在任意時間自由進行。挑戰者可以選擇一個時段向當前的鑄幣者發起挑戰。為防止濫用挑戰，挑戰者需要支付一筆較高的挑戰費。當挑戰者發布一個競爭交易后，協議將檢查競爭者與當前鑄幣者的質押權益以決定誰是競爭的勝出者。

7. 鑄幣經濟

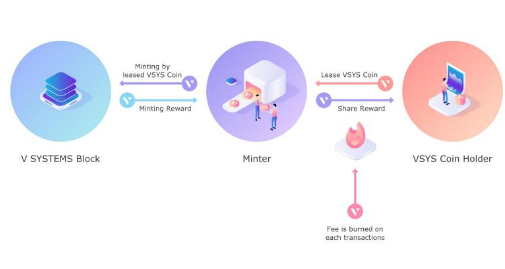
鑄幣者參與鑄幣的質押權益包括其擁有的且未租借給別人的數字貨幣，以及其他用戶租借給該鑄幣者的數字貨幣。術語“租借（lease）”指明的關系為鑄幣者通常以鑄幣池形式運行，并需要給數字貨幣的擁有者支付一定利利息。在租借期間，貨幣的所有權并未轉讓，因此鑄幣者不能花費或轉讓租借來的貨幣。

鑄幣時段的平等鑄幣權使得網絡中超級節點擁有平等的地位及相同的鑄幣輸出。這與比特幣挖礦設計形成鮮明對比。在比特幣挖礦中，沒有內在機制防止礦池市場形成壟斷，其已成為了系統去中心化目標的一個現實威脅。

鑄幣時段的平等鑄幣權在鑄幣經濟中扮演了了一個不可或缺的角色。超級節點形成了一個由鑄幣池組成的市場。鑄幣池市場決定租借的利率。由于權益所有者有將權益租借給支付更高利率的超級節點的理性偏好，而對于支付高利率的超級節點來說，鑄幣輸出（即收入）是固定的，租借來更多的權益將會迫使它降低租借利率，所以存在一個平衡點，其作為一種內在的力量迫使超級節點的租借利率趨于相等。

V SYSTEMS 平臺也采用了Peercoin 的手續費銷毀模型以降低通脹率，同時消除鑄幣者之間的利益摩擦。

對超級節點硬件資源的要求將通過共識協議范疇之外的社區力量進行標準化與提升。

8. 權益流動性與頻繁競爭攻擊

以往的權益證明共識系統對于權益在參與鑄幣后的移動行為進行了諸多限制。盡管在技術層面這可能有其合理考慮，但在經濟層面，它卻是用戶參與鑄幣的一個進入門檻。

然而，在權益證明共識中，參與鑄幣的權益數量直接關系到共識的安全等級。從這個意義上講，對權益的移動不加任何限制是對網絡安全有益的。稱不限制權益移動的這種性質為權益流動性（stake liquidity）。有了權益流動性，鑄幣者可以隨時花費或轉讓其擁有的權益。而租借權益的人也可以隨時解除租借關系，并花費或轉讓其權益。

權益流動性也引入了某些攻擊的可能性。從權益證明的角度來看，不應當允許使用同一權益在多個鑄幣時段索取鑄幣權。然而由于權益具有流動性，或許可以利用這種流動性嘗試快速移動權益， 為權益獲取比其應得的更多的鑄幣時段。稱這種類型的攻擊為頻繁競爭攻擊（busy contention attack）。

抵抗這類攻擊的辦法是為賬戶余額引入某種度量，其類似于鑄幣時段競爭的累加平均。思路是，權益必須留存在賬戶中一段時間，以等待賬戶度量恢復到滿額，這樣即可阻止頻繁競爭攻擊。

9. 賬戶模型與余額

傳統的記賬系統使用賬戶模型，它密切監測一個稱為余額的可變狀態以及相應交易歷史。比特幣內部使用了一種不同的形式，我們稱之為幣袋（coinbag）模型。想要獲得賬戶余額，則需要收集與賬戶或地址相關聯的幣袋信息，并將各個幣袋的貨幣數目相加得到余額。過去幾年，許多加密貨幣系統都用回了更傳統的賬戶模型。V SYSTEMS 也采用了賬戶模型，使得能更有效監測余額。

定義了租借關系之后，每個賬戶的基本余額可以描述為兩個不同的部分：一是標準余額（regular balance），即用戶擁有的余額；另一個是鑄幣余額（minting balance），它是標準余額加上租借來的余額并減去租借出去的部分。這兩種不同的余額會隨著相關交易易的確認而即時變動。

10. 關于余額模式的提議

10.1 幣齡

幣齡（coin age）被定義貨幣數量與持幣周期之積。例如，以幣天（coin-day）為單位的幣齡就是貨幣數量與持有這些貨幣的天數的乘積。

仍使用 Peercoin 白皮書中的例子，如果 Bob 從 Alice 那里收到 10 個幣并持有這些幣 90天，那么我們就稱 Bob 累積的幣齡為 900 幣天。另外，當 Bob 花掉了從 Alice 那里接收到的 10 個幣時，就稱 Bob 用這 10 個幣累積的幣齡已經被消費（或銷毀）了。

作為控制鑄幣概率的價值證明，幣齡顯示出了它的優點與穩定性。然而，由于它是一個基于交易的量，計算復雜度與給定時間內所執行的交易數量有關。而且，幣齡也并不是一個能體現出鑄幣者對社區貢獻量大小的準確值。

10.2 已確認余額

已確認余額（confirmed balance）指的是經 N 個區塊確認之后的鑄幣余額（總的標準余額 + 租入 -租出）。

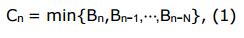
其中，Bi 是在？高度為 i 的區塊中的鑄幣余額。N 是一個用來估計作？用區間的常數。已確認余額的優點包括：

· 余額不不會因某些大額輸入而立即增加，但會因大額轉出而立即減少；

· 為了得到一個很？高的已確認余額，礦工/鑄幣者需要收集并長時間持有貨幣。

然而，已確認余額本身也有缺點：

· 在一段時間內連續或累積的輸入不不影響這段時間內的余額計算；

· 計算復雜度為 O（N ）。對于高速鑄幣情形，為了了達到較好的性能與較高的穩定性，需要選取一個較大的 N。此時，O（N ） 算法將會是對系統性能造成影響的一個因素。

10.3 關于余額計算方式的提議

10.3.1 加權平均余額

為克服已確認余額的缺點，并降低計算復雜度，我們需要為高速挖礦/鑄幣的區塊鏈系統設計一個新的、有更多性質且更容易計算的余額模式。

借鑒操作系統平均負載以及隨機過程公式的思想，我們設計了如下加權平均余額：

這一新余額模式的計算復雜度降到了O（1） ，只需在每次鑄幣余額發生變動時記錄一下加權平均余額。而且該模式下余額的最快增長速度是線性的（參看例11.1）。但是，從例11.1.1 及例 11.1.2 可以看出，如果余額頻繁變動，則加權平均余額的下降速度會變慢。此外，這也是一個好的性質，只要總的加權平均余額受控的話。受控意味著余額不會莫名其妙地被創造出來（類似于物理學中的能量守恒律）。從例11.2.1 及例11.2.2 可以得出加權平均余額公式并不滿足守恒律。

10.3.2 鑄幣平均余額

為使加權平均余額擁有好的性質，并克服其缺點，我們提出一個新的余額模式，稱為鑄幣平均余額（MAB），其定義如下：

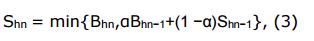
其中，Bhn 表示高度在 hn 時的當前余額。

鑄幣平均余額是取當前余額與加權平均余額的較小者。計算復雜度仍為 O（1） 。而且，在這個公式中，如果用戶將其所有余額轉出，則 MAB 會直接減為 0。有了了這個性質，總的鑄幣平均余額將會是守恒的，且被總余額所控制。

11. 一些例子

本章中，我們將設計許多數值實例例以展示鑄幣平均余額的性質。假設鑄幣的速度為每秒一個區塊，則一天中可以得到 24 ×60 ×60 = 86400 個區塊。本章中，我們對所有例子都取 N = 86400。而且作為理想情形，我們也令所有交易手續費為 0。

11.1 增長與下降速率

本章的第一個例例子是關于余額增長與下降速率的。

11.1.1 簡化的增長與下降速率

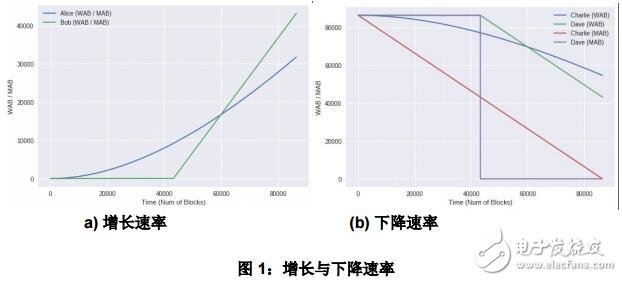
設 Alice 與 Bob 的初始余額都為 0。Alice 在每個區塊產生時都能得到 1 個幣，而 Bob 在高度為 43200 的區塊上可一次性獲得 86400 個幣。Alice 的增長表現可用幾何級數公式計算。圖 1a 展示了一天內 Alice 與 Bob 的加權平均余額以及鑄幣平均余額的表現。

類似地，設 Charlie 與 Dave 的初始余額/WAB/MAB 都為 86400。Charlie 每個區塊都減少 1 個幣，而 Dave 在高度為 43200 的區塊中失去 86400 個幣。圖 1b 展示了了一天內Charlie 與 Dave 的加權平均余額以及鑄幣平均余額的表現。

11.1.2 緩慢下降速率

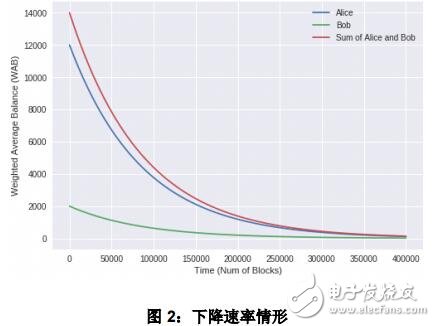
設 Alice 和 Bob 分別有初始加權平均余額 12000 和 2000。設初始區塊高度為奇數，僅Bob 有余額 1，且 Bob 在區塊高度為奇數里將他所有余額轉給 Alice。類似地，在區塊高度為偶數時， Alice 將其所有余額轉給 Bob。圖 2 展示了400000 個區塊內 Alice 與 Bob的加權平均余額情況。可以看到兩者 WAB 之和在緩慢下降。而如果 Alice 與 Bob 在這段時間內沒做任何動作，那么他們 WAB 之和應當在高度為 86400 時等于 1。

11.2 余額守恒律律

我們將給出幾個例子來說明鑄幣平均余額（MAB）的良好性質。

11.2.1 守恒律律

在這個例子中，Alice 與 Charlie 的初始 WAB 以及余額均為 100，而 Bob 與 Dave 的初始WAB 與余額均為 0。在高度 h =0 時，Charlie 向 Dave 轉了100 個幣。在另一個組中，Alice 與 Bob 將每隔 10800 個區塊交換一下他們的余額。圖 3 表明每個組中的總余額是守恒的。

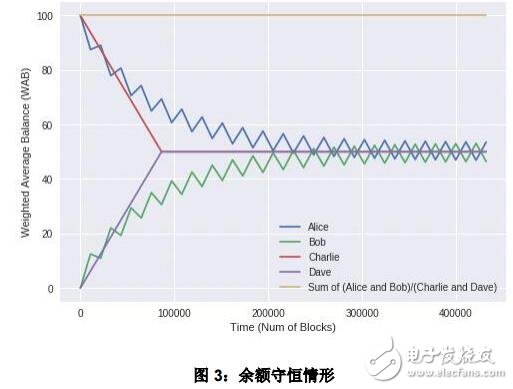
11.2.2 非守恒情形

在這個例子中，Alice 的初始 WAB/MAB 以及余額均為 100，而 Bob 與 Charlie 的初始 WAB/ MAB 以及余額均為 0。在高度 h =0 時，Alice 向 Charlie 轉出 80 個幣。而后，Alice 與 Bob 每隔 10800 個區塊交換一下余額。圖 4a 與 4b 顯示了了兩個余額計算公式之間的差異。

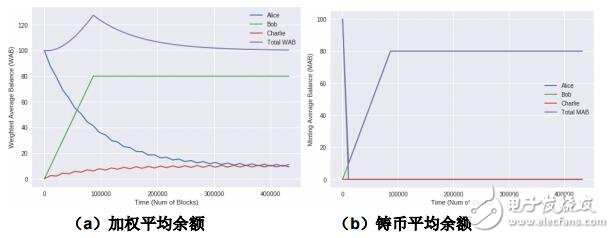
從圖 4a 可以看出總的 WAB 在某些區間內會超過 100，即意味著利用某些“好”的策略略可以創造更多的 WAB。然而，圖 4b 表明總的 MAB 總是小于 100，而這在實際應用中是一個好的性質。

11.3 鑄幣者的鑄幣平均余額

在本例例中，我們將展示一些關于鑄幣者的情況。第一個鑄幣者的初始余額 100，而初始WAB/ MAB 均為 0。鑄幣獎勵為每分鐘 1 個幣。

圖 5 展示了了一天內 WAB、MAB 以及余額的變化情況。

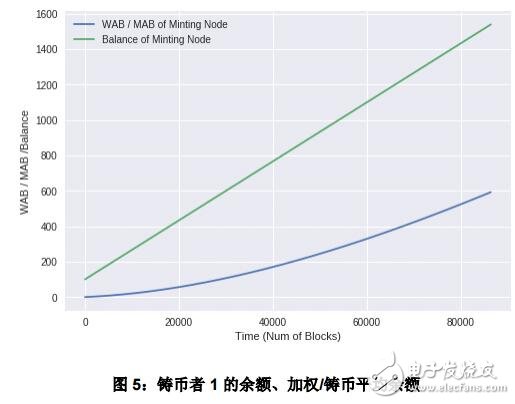
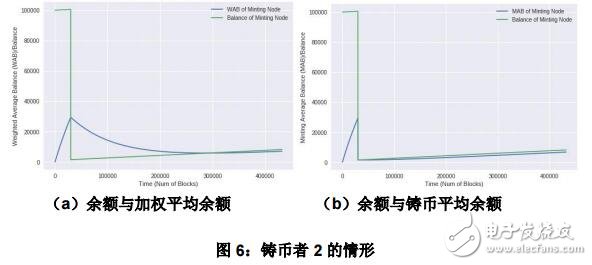
第二個鑄幣者的初始余額為 10000，初始 WAB/MAB 為 0。鑄幣獎勵仍為每分鐘 1 個幣。在高度為 500 時，鑄幣者將其余額內的 99000 個幣轉出。

圖 6a 及 6b 展示了了在五天內 WAB、MAB 以及余額的變化情況。

12. 總結

超級節點權益證明共識（SPoS）是朝著高性能區塊鏈系統的一個演化過程。生態資源可以更更有效地向超級節點的硬件升級傾斜，系統響應不不僅更更快？而且更更加可預測、更更加穩定。我們也設計了了鑄幣平均余額以？支持權益流動性。