自 2012 年以來,深度學習的發展有目共睹,今年 3 月,為此做出巨大貢獻的 Yoshua Bengio、Yann Lecun和Geofrey Hinton 一同獲得了圖靈獎。但現在,深度學習需要被進一步挖掘。
在最近一次采訪中,圖靈獎得主Bengio再次再次警示了可解釋因果關系對深度學習發展的重要性。
在他看來,除非深度學習能夠超越模式識別并了解因果關系的更多信息,否則它將無法實現其全部潛力,也不會帶來真正的AI革命。換句話說,深度學習需要開始知道事情發生的因果關系,這將使現有的 AI 系統更加智能,更加高效。
不過,對于深度學習未來發展的具體思路,AI 大佬們也有不同意見,在前幾日,紐約大學教授 Gary Marcus 和 Bengio 就此來了一場隔空“互懟”。
不管怎樣,Bengio 在研究深度學習可解釋性方面已經出發了。今年年初,他其他研究者合作發表了《通過元遷移目標來學習理解因果關系》一文,提出了一種基于學習器適應稀疏分布變化速度的元學習因果結構,還生成了因果關系的綜合數據集。
以下為這篇論文的主要內容要點,AI科技大本營(ID:rgznai100)編譯:
本文提出了一種基于學習器適應稀疏分布變化速度的元學習因果結構,這些變化因素如干預,智能體的行為和其他不穩定因素。本文表明,在這種假設下,正確的因果結構選擇會使學習器更快適應修改后的分布,因為當對所學知識進行適當模塊化時,分布變化僅會集中在一種或幾種機制中。這導致為了適應這種變化,需要重新學習梯度和一些自由度較低的參數。并將適應修改后分布的速度作為元學習目標的激勵項。
本文闡述了如何將其用于確定兩個觀察到的變量之間的因果關系。分布的變化不需要對應于某種標準的干預(固定變量),并且學習器不會了解這些干預相關的知識。本文證明了因果結構可以通過連續變量和端到端的學習進行參數化。然后,本文探討了如何將這些想法用于學習一種編碼器,該編碼器能將初級觀察變量映射到未觀察到的因果變量,從而導致更快的分布適應。它學習的是一種表示空間,在這種表示空間中,可以滿足獨立性以及微小和稀疏變化的假設。
引言
當目前的機器學習方法需要泛化到訓練分布之外的場景時,模型的能力似乎很薄弱,而這通常是非常需要的。在與訓練數據相同的分布相似的測試集上獲得良好的泛化性能是不夠的,我們還希望在一種數據集中學到的知識能夠很好的泛化到其他相關的分布中。這些分布可能涉及模型之前所見的內容,而它的一些變化則是由智能體引起的。
更籠統地說,我們希望以前學到的知識形成一個豐富的基礎,從中可以非常迅速地適應新的但相關的分布,即獲得良好的遷移。可能模型必須學習一些新內容,但是由于它已經掌握了大多數其他相關內容(以及它們的組成方式),因此在遷移目標分布上,可以非常快速的完成學習。
沒有任何假設,就不可能成功遷移到一個無關的分布上。在本文中,我們關注于以下假設:當以適當的模塊化方式表示知識時,改變是稀疏的,即只有一個或幾個模塊更改了。當分布變化是由于一種或多種因素的作用引起的,這尤其相關,例如因果關系文獻中討論的干預措施,其中單個因果變量被限制在特定值。
總的來說,模型很難一次影響許多潛在的因果變量,盡管本文并不是關于模型學習,但這是我們建議在此處利用的一個特性,用于幫助發現這些變量它們之間的因果關系。
為了激發推斷因果結構的需求,需要考慮可以實際執行或可以想象的干預。可以想象一下,由于一項干預措施,可能會改變相關變量的聯合分布,即以前從未觀察到過。這超出了遷移學習的范圍,因此需要因果學習和因果推理。
為此,僅學習觀測變量的聯合分布是不夠的。人們還應該對潛在的高級變量及其因果關系有足夠的了解,以能夠正確推斷干預的效果。例如,A =下雨,它會導致B =打開雨傘(反之亦然)。改變下雨的邊緣概率(例如,因為天氣變化)不會改變A和B的之間的關系(即P(B | A)),但會對邊緣概率P(B)卻產生了影響。相反,智能體對B(打開雨傘)的干預不會對A(下雨)的邊緣分布產生影響。通常僅從(A,B)訓練對中看不到這種不對稱性,直到發生分布變化(例如由于干預引起的)。
這是本文的動機,在本文中,人們可以從不一定是已知的干預措施分布中學習,而不僅僅是獲取一個聯合分布,還可以發現一些潛在的因果結構。機器學習方法通常會利用某種形式的關于數據分布的假設。在本文中,我們不僅要考慮數據分布的假設,還要考慮其變化方式(例如,從訓練分布轉到遷移分布時,可能是由于某些智能體的行為造成的)。
我們建議基于這樣的假設:當表示有關分布的知識時,其中的變化很小。之所以出現這種情況,是因為一個或幾個基本事實機制的假設(但很難直接驗證),會因為某種干預形式而改變。
我們如何利用這個假設?如果我們擁有正確的知識表示,那么從一個訓練好的模型開始,我們應該能快速適應遷移的分布。之所以出現這種情況,是因為我們假設數據的生成過程是獨立獲得的,而且從訓練分布到轉移分布,幾乎不需要改變真正的機制和參數。因此,捕獲相應知識分解的模型僅需要進行一些更新和一些樣例,即可適應遷移分布。
因此,基于正確知識表示空間的微小變化的假設,我們可以定義一個衡量適應速度的元學習目標,以便優化知識的表示,分解和結構化方式。這是本文提出的核心思想。
請注意,當存在更多的非平穩性(即分布變化很多)時,可以獲得更強的信號,就像在元學習中一樣,通過更多的元示例獲得更好的結果。通過這種方式,我們可以將通常被認為是機器學習中令人討厭的東西(由于非平穩性,不受控制的干預等導致的分布變化)轉化為訓練信號,從而找到一種將知識分解為要素和知識的好方法。
在本文中,我們將通過對合成生成的數據進行特定的實驗來探索上述想法,以便對其進行驗證并證明存在利用它們的簡單算法。但是,對我們來說很明顯,將需要更多的工作來評估提出方法的多樣性。設置以及具有不同的具體參數設置,訓練目標,環境等。
我們從最簡單的設置開始,并評估上述方法是否可用于了解因果關系的方向。然后,我們研究獲得訓練信號的關鍵問題,該訓練信號關于如何將原始觀測數據轉換為表示空間,在該表示空間中,潛在變量可以通過具有稀疏分布變化的稀疏因果圖來建模,并顯示正確的編碼器確實可以更好地實現我們期望的元學習目標的價值。
何為因?何為果?
作者在本節中考慮確定變量A是否導致變量B或反之的問題。學習器(模型)會從一對相關分布中觀察訓練樣本(a,b),按照慣例,我們將其稱為訓練分布和遷移分布。請注意,僅基于來自單個(訓練)分布的樣本,通常A→B模型(A導致B)和B→A模型(反之亦然,請參見下面的公式(1))另請參見附錄A中的理論論證和模擬結果。
為了突出提出的元學習目標的功能,我們考慮了很多可用于訓練分布但不能用于遷移分布的樣例。實際上,正如我們將在下面討論的那樣,如果我們可以訪問更多短時遷移的樣例,則推斷出正確因果方向的訓練信號會更強烈。
學習帶兩個離散變量的因果關系圖
我們需要比較兩個假設(A→B與B→A)的性能,即兩個模型在訓練分布上進行訓練后在遷移分布上的適應速度。我們將在此參數上假設簡單的隨機梯度下降,但是當然可以使用其他過程。在不失一般性的前提下,令A→B為正確的因果模型。為了使條件更強,可以考慮兩個分布之間的變化等于原因A的真實P(A)值的隨機變化(因為這會對效果B產生影響,并揭示因果關系方向)。我們不假定學習器(模型)知道進行了何種干預,這與更常見的因果發現和受控實驗方法不同。我們僅假設發生了某些變化,然后嘗試利用它來揭示結構性的因果信息。
適應遷移分布的實驗
本文目前進行的實驗是將正確因果模型的學習曲線與遷移模型上的因果模型的學習曲線進行了比較。對于來自不同但相關的遷移分布的數據,僅需幾個梯度步驟,我們的元學習算法就可以獲取至關重要的一些信息(信號)。為了展示這種適應的效果,僅使用遷移分布中的少量數據,本文對離散隨機變量的模型進行了實驗。如上圖1。
一個簡單的參數計數能有助于我們理解圖1中的觀察結果。首先,考慮在適應遷移分布的階段,指定不同模塊參數的預期梯度,并對應于學習的元示例。作者提出了三個見解
見解1對于在訓練階段已正確學習的模塊參數,遷移分布相對于模塊參數的預期梯度為零,并且具有正確的因果關系集合,對應于正確的因果圖,如果(c)相應的正確條件分布沒有從訓練分布變為遷移分布。
見解2上述公式(2)中遷移數據的負對數似然率的梯度。其結構參數由下式給出
其中D2是遷移數據,而
是假設A->B的后驗概率。此外,這可以等效地寫為
其中
是遷移數據D2上兩個假設對數似然之間的差異。
見解3
隨機梯度下降(適當降低學習率)趨向于
作者通過附錄及實驗證實了上述三個見解,具體可以參見論文。
總結展望
作者使用非常簡單的雙變量設置,確定了學習器可以用適應觀察數據分布稀疏變化的速率來選擇或優化因果結構并解耦因果變量。基于這樣的假設:在具有正確因果結構的情況下,這些分布變化是局部且稀疏的。本文通過理論結果和實驗驗證了這些想法。
這項工作只是基于修改分布速率優化因果結構的第一步。在實驗方面,除了本文研究的設定外,還應考慮許多其他條件設定,包括各種參數設置,更豐富和更大的因果圖,各種優化程序等。此外,由于我們在這一點上僅使用了具有單一自由度的最簡單的編碼器進行了實驗,在探索如何學習更優的學習表達時,還需要更多的工作。擴充這些想法,便能應用于提升學習器處理非平穩性的分布,從而提高學習器的魯棒性。
-
AI
+關注
關注
88文章
34691瀏覽量
276649 -
深度學習
+關注
關注
73文章
5557瀏覽量
122621
發布評論請先 登錄
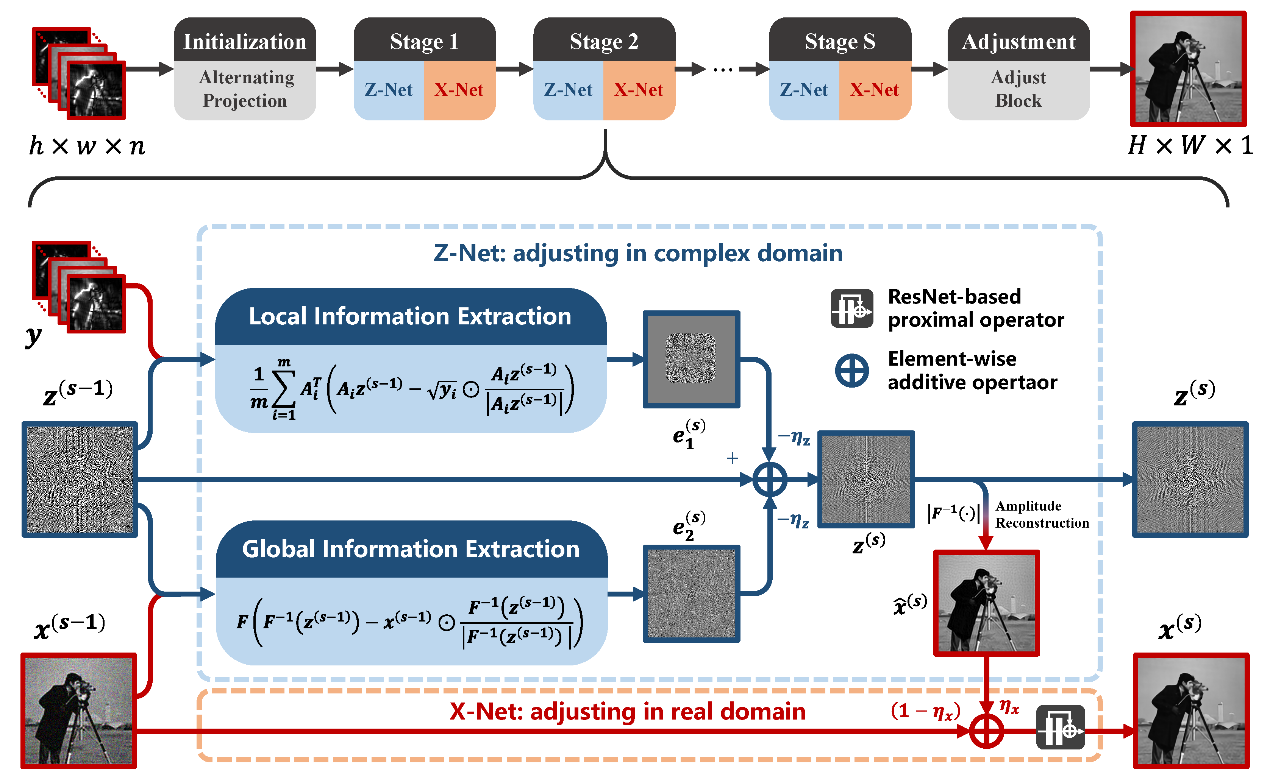
中國科學院西安光機所在計算成像可解釋性深度學習重建方法取得進展
BP神經網絡與深度學習的關系
小白學解釋性AI:從機器學習到大模型

NPU與機器學習算法的關系
NPU在深度學習中的應用
當系統鬧脾氣:用「因果推斷」哄穩技術的心
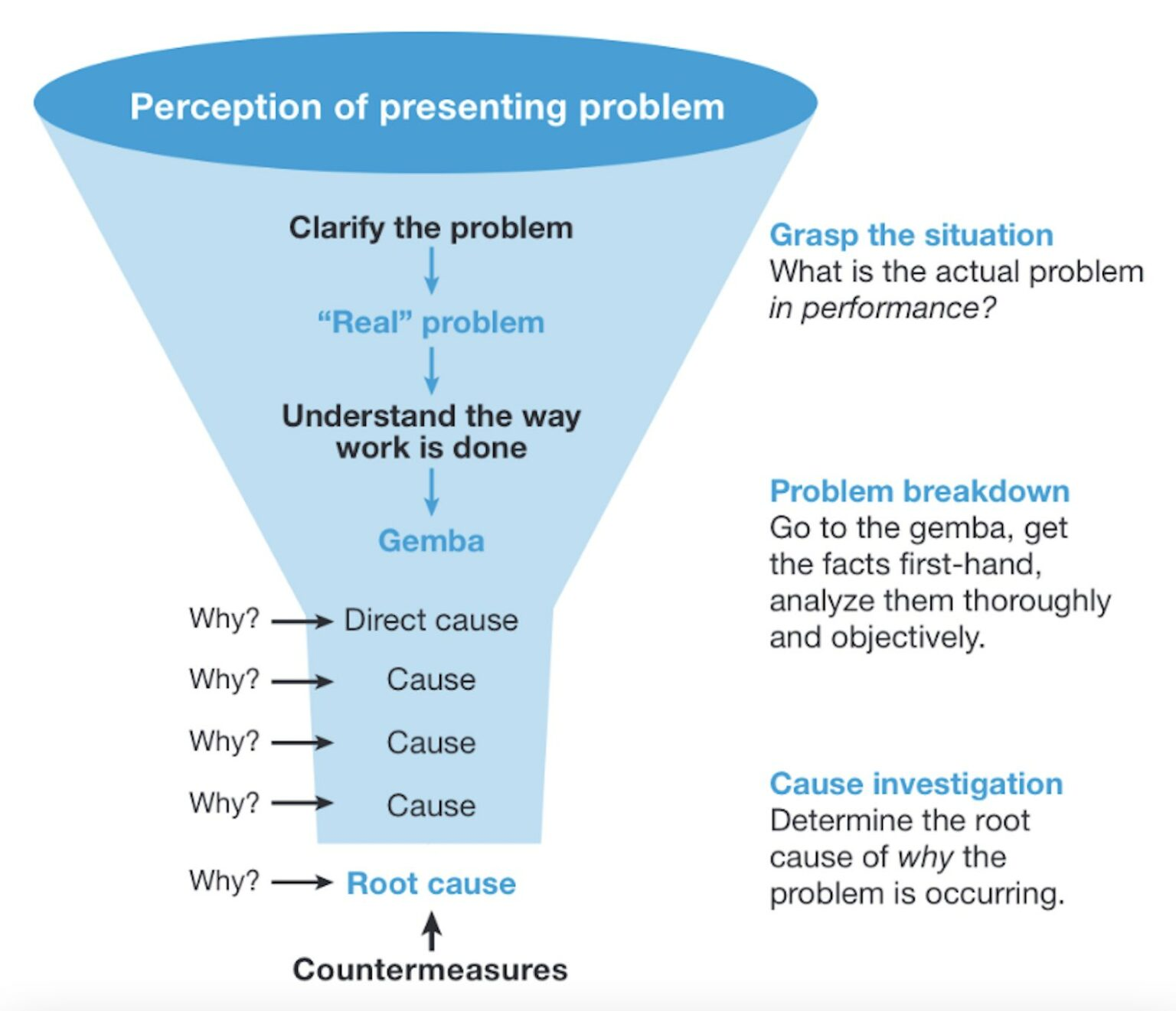





 可解釋因果關系對深度學習的影響
可解釋因果關系對深度學習的影響











評論