網上關于各種降維算法的資料參差不齊，同時大部分不提供源代碼。這里有個 GitHub 項目整理了使用 Python 實現了 11 種經典的數據抽取（數據降維）算法，包括：PCA、LDA、MDS、LLE、TSNE 等，并附有相關資料、展示效果;非常適合機器學習初學者和剛剛入坑數據挖掘的小伙伴。一、為什么要進行數據降維？

所謂降維，即用一組個數為 d 的向量 Zi 來代表個數為 D 的向量 Xi 所包含的有用信息，其中 d《D，通俗來講，即將高維度下降至低維度；將高維數據下降為低維數據。通常，我們會發現大部分數據集的維度都會高達成百乃至上千，而經典的 MNIST，其維度都是 64。

MNIST 手寫數字數據集但在實際應用中，我們所用到的有用信息卻并不需要那么高的維度，而且每增加一維所需的樣本個數呈指數級增長，這可能會直接帶來極大的「維數災難」;而數據降維就可以實現：

使得數據集更易使用

確保變量之間彼此獨立

降低算法計算運算成本

去除噪音一旦我們能夠正確處理這些信息，正確有效地進行降維，這將大大有助于減少計算量，進而提高機器運作效率。而數據降維，也常應用于文本處理、人臉識別、圖片識別、自然語言處理等領域。

二、數據降維原理

往往高維空間的數據會出現分布稀疏的情況，所以在降維處理的過程中，我們通常會做一些數據刪減，這些數據包括了冗余的數據、無效信息、重復表達內容等。例如：現有一張 1024*1024 的圖，除去中心 50*50 的區域其它位置均為零值，這些為零的信息就可以歸為無用信息;而對于對稱圖形而言，對稱部分的信息則可以歸為重復信息。

因此，大部分經典降維技術也是基于這一內容而展開，其中降維方法又分為線性和非線性降維，非線性降維又分為基于核函數和基于特征值的方法。

線性降維方法：PCA 、ICA LDA、LFA、LPP（LE 的線性表示）

非線性降維方法：

基于核函數的非線性降維方法——KPCA 、KICA、KDA

基于特征值的非線性降維方法（流型學習）——ISOMAP、LLE、LE、LPP、LTSA、MVU

哈爾濱工業大學計算機技術專業的在讀碩士生 Heucoder 則整理了 PCA、KPCA、LDA、MDS、ISOMAP、LLE、TSNE、AutoEncoder、FastICA、SVD、LE、LPP 共 12 種經典的降維算法，并提供了相關資料、代碼以及展示，下面將主要以 PCA 算法為例介紹降維算法具體操作。

三、主成分分析（PCA）降維算

PCA 是一種基于從高維空間映射到低維空間的映射方法，也是最基礎的無監督降維算法，其目標是向數據變化最大的方向投影，或者說向重構誤差最小化的方向投影。它由 Karl Pearson 在 1901 年提出，屬于線性降維方法。與 PCA 相關的原理通常被稱為最大方差理論或最小誤差理論。這兩者目標一致，但過程側重點則不同。

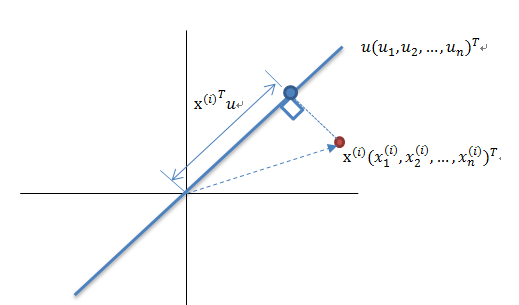
最大方差理論降維原理將一組 N 維向量降為 K 維（K 大于 0，小于 N），其目標是選擇 K 個單位正交基，各字段兩兩間 COV（X，Y） 為 0，而字段的方差則盡可能大。因此，最大方差即使得投影數據的方差被最大化，在這過程中，我們需要找到數據集 Xmxn 的最佳的投影空間 Wnxk、協方差矩陣等，其算法流程為：

算法輸入：數據集 Xmxn;

按列計算數據集 X 的均值 Xmean，然后令 Xnew=X?Xmean;

求解矩陣 Xnew 的協方差矩陣，并將其記為 Cov;

計算協方差矩陣 COV 的特征值和相應的特征向量;

將特征值按照從大到小的排序，選擇其中最大的 k 個，然后將其對應的 k 個特征向量分別作為列向量組成特征向量矩陣 Wnxk;

計算 XnewW，即將數據集 Xnew 投影到選取的特征向量上，這樣就得到了我們需要的已經降維的數據集 XnewW。

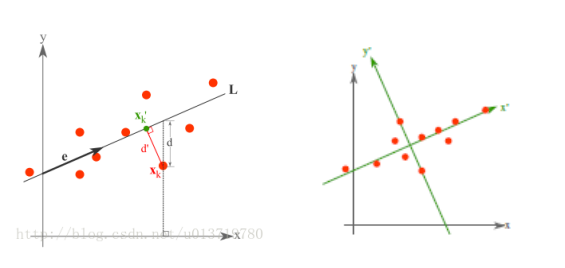
最小誤差理論降維原理而最小誤差則是使得平均投影代價最小的線性投影，這一過程中，我們則需要找到的是平方錯誤評價函數 J0（x0） 等參數。

詳細步驟可參考《從零開始實現主成分分析 （PCA） 算法》：https://blog.csdn.net/u013719780/article/details/78352262

主成分分析（PCA）代碼實現

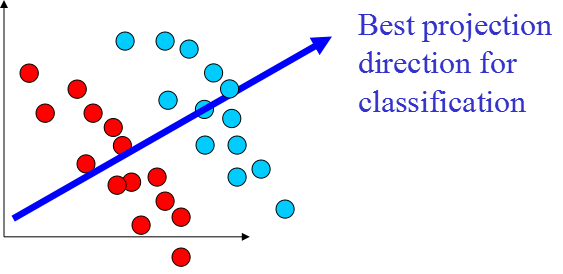
關于 PCA 算法的代碼如下：

from __future__ import print_function

from sklearn import datasets

import matplotlib.pyplot as plt

import matplotlib.cm as cmx

import matplotlib.colors as colors

import numpy as np

%matplotlib inline

def shuffle_data（X， y， seed=None）：

if seed：

np.random.seed（seed）

idx = np.arange（X.shape［0］）

np.random.shuffle（idx）

return X［idx］， y［idx］

# 正規化數據集 X

def normalize（X， axis=-1， p=2）：

lp_norm = np.atleast_1d（np.linalg.norm（X， p， axis））

lp_norm［lp_norm == 0］ = 1

return X / np.expand_dims（lp_norm， axis）

# 標準化數據集 X

def standardize（X）：

X_std = np.zeros（X.shape）

mean = X.mean（axis=0）

std = X.std（axis=0）

# 做除法運算時請永遠記住分母不能等于 0 的情形

# X_std = （X - X.mean（axis=0）） / X.std（axis=0）

for col in range（np.shape（X）［1］）：

if std［col］：

X_std［：， col］ = （X_std［：， col］ - mean［col］） / std［col］

return X_std

# 劃分數據集為訓練集和測試集

def train_test_split（X， y， test_size=0.2， shuffle=True， seed=None）：

if shuffle：

X， y = shuffle_data（X， y， seed）

n_train_samples = int（X.shape［0］ * （1-test_size））

x_train， x_test = X［：n_train_samples］， X［n_train_samples：］

y_train， y_test = y［：n_train_samples］， y［n_train_samples：］

return x_train， x_test， y_train， y_test

# 計算矩陣 X 的協方差矩陣

def calculate_covariance_matrix（X， Y=np.empty（（0，0）））：

if not Y.any（）：

Y = X

n_samples = np.shape（X）［0］

covariance_matrix = （1 / （n_samples-1）） * （X - X.mean（axis=0））.T.dot（Y - Y.mean（axis=0））

return np.array（covariance_matrix， dtype=float）

# 計算數據集 X 每列的方差

def calculate_variance（X）：

n_samples = np.shape（X）［0］

variance = （1 / n_samples） * np.diag（（X - X.mean（axis=0））.T.dot（X - X.mean（axis=0）））

return variance

# 計算數據集 X 每列的標準差

def calculate_std_dev（X）：

std_dev = np.sqrt（calculate_variance（X））

return std_dev

# 計算相關系數矩陣

def calculate_correlation_matrix（X， Y=np.empty（［0］））：

# 先計算協方差矩陣

covariance_matrix = calculate_covariance_matrix（X， Y）

# 計算 X， Y 的標準差

std_dev_X = np.expand_dims（calculate_std_dev（X）， 1）

std_dev_y = np.expand_dims（calculate_std_dev（Y）， 1）

correlation_matrix = np.divide（covariance_matrix， std_dev_X.dot（std_dev_y.T））

return np.array（correlation_matrix， dtype=float）

class PCA（）：

“”“

主成份分析算法 PCA，非監督學習算法。

”“”

def __init__（self）：

self.eigen_values = None

self.eigen_vectors = None

self.k = 2

def transform（self， X）：

“”“

將原始數據集 X 通過 PCA 進行降維

”“”

covariance = calculate_covariance_matrix（X）

# 求解特征值和特征向量

self.eigen_values， self.eigen_vectors = np.linalg.eig（covariance）

# 將特征值從大到小進行排序，注意特征向量是按列排的，即 self.eigen_vectors 第 k 列是 self.eigen_values 中第 k 個特征值對應的特征向量

idx = self.eigen_values.argsort（）［：：-1］

eigenvalues = self.eigen_values［idx］［：self.k］

eigenvectors = self.eigen_vectors［：， idx］［：， ：self.k］

# 將原始數據集 X 映射到低維空間

X_transformed = X.dot（eigenvectors）

return X_transformed

def main（）：

# Load the dataset

data = datasets.load_iris（）

X = data.data

y = data.target

# 將數據集 X 映射到低維空間

X_trans = PCA（）.transform（X）

x1 = X_trans［：， 0］

x2 = X_trans［：， 1］

cmap = plt.get_cmap（‘viridis’）

colors = ［cmap（i） for i in np.linspace（0， 1， len（np.unique（y）））］

class_distr = ［］

# Plot the different class distributions

for i， l in enumerate（np.unique（y））：

_x1 = x1［y == l］

_x2 = x2［y == l］

_y = y［y == l］

class_distr.append（plt.scatter（_x1， _x2， color=colors［i］））

# Add a legend

plt.legend（class_distr， y， loc=1）

# Axis labels

plt.xlabel（‘Principal Component 1’）

plt.ylabel（‘Principal Component 2’）

plt.show（）

if __name__ == “__main__”：

main（）

最終，我們將得到降維結果如下。其中，如果得到當特征數 （D） 遠大于樣本數 （N） 時，可以使用一點小技巧實現 PCA 算法的復雜度轉換。

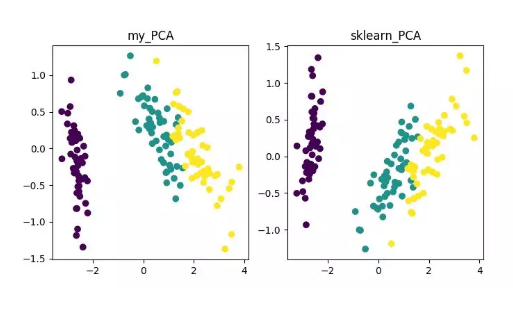
PCA 降維算法展示當然，這一算法雖然經典且較為常用，其不足之處也非常明顯。它可以很好的解除線性相關，但是面對高階相關性時，效果則較差;同時，PCA 實現的前提是假設數據各主特征是分布在正交方向上，因此對于在非正交方向上存在幾個方差較大的方向，PCA 的效果也會大打折扣。

四、其它降維算法及代碼地址

KPCA（kernel PCA）

KPCA 是核技術與 PCA 結合的產物，它與 PCA 主要差別在于計算協方差矩陣時使用了核函數，即是經過核函數映射之后的協方差矩陣。引入核函數可以很好的解決非線性數據映射問題。kPCA 可以將非線性數據映射到高維空間，在高維空間下使用標準 PCA 將其映射到另一個低維空間。

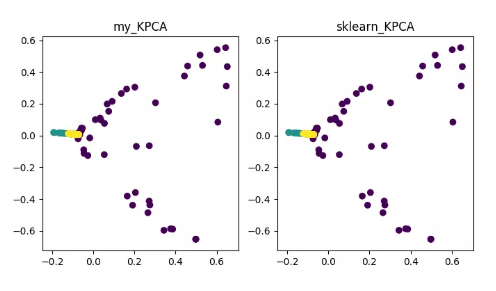
KPCA 降維算法展示詳細內容可參見 《Python 機器學習》之特征抽取——kPCA：https://blog.csdn.net/weixin_40604987/article/details/79632888代碼地址：https://github.com/heucoder/dimensionality_reduction_alo_codes/blob/master/codes/PCA/KPCA.py

LDA（Linear Discriminant Analysis）LDA 是一種可作為特征抽取的技術，其目標是向最大化類間差異，最小化類內差異的方向投影，以利于分類等任務即將不同類的樣本有效的分開。LDA 可以提高數據分析過程中的計算效率，對于未能正則化的模型，可以降低維度災難帶來的過擬合。

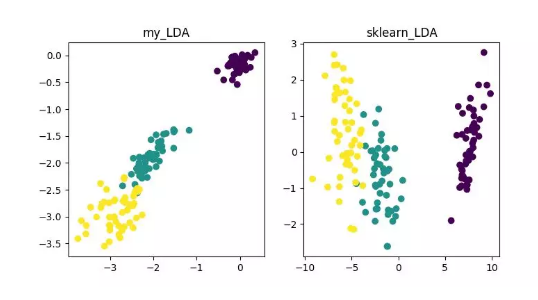
LDA 降維算法展示詳細內容可參見《數據降維—線性判別分析（LDA）》：https://blog.csdn.net/ChenVast/article/details/79227945代碼地址：https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master/codes/LDA

MDS（multidimensional scaling）MDS 即多維標度分析，它是一種通過直觀空間圖表示研究對象的感知和偏好的傳統降維方法。該方法會計算任意兩個樣本點之間的距離，使得投影到低維空間之后能夠保持這種相對距離從而實現投影。由于 sklearn 中 MDS 是采用迭代優化方式，下面實現了迭代和非迭代的兩種。

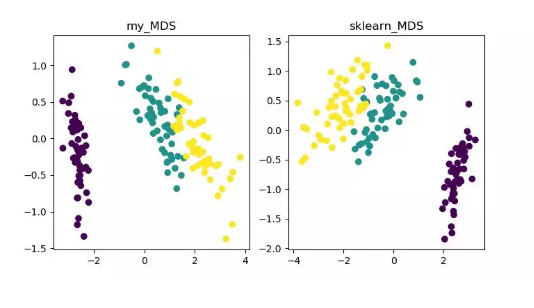
MDS 降維算法展示詳細內容可參見《MDS 算法》https://blog.csdn.net/zhangweiguo_717/article/details/69663452代碼地址：https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master/codes/MDS

ISOMAPIsomap 即等度量映射算法，該算法可以很好地解決 MDS 算法在非線性結構數據集上的弊端。MDS 算法是保持降維后的樣本間距離不變，Isomap 算法則引進了鄰域圖，樣本只與其相鄰的樣本連接，計算出近鄰點之間的距離，然后在此基礎上進行降維保距。

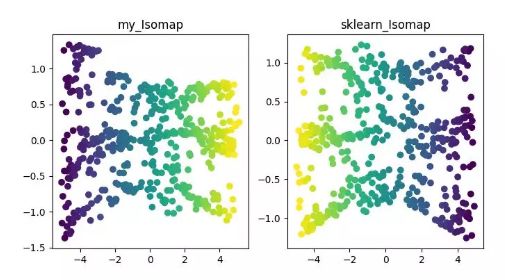
ISOMAP 降維算法展示
責任編輯:pj