卡爾曼濾波實(shí)質(zhì)上就是基于觀測值以及估計(jì)值二者的數(shù)據(jù)對真實(shí)值進(jìn)行估計(jì)的過程。預(yù)測步驟如圖1所示:
圖1 卡爾曼濾波原理流程圖
假設(shè)我們能夠得到被測物體的位置和速度的測量值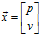 ,在已知上一時(shí)刻的最優(yōu)估計(jì)值
,在已知上一時(shí)刻的最優(yōu)估計(jì)值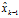 以及它的協(xié)方差矩陣
以及它的協(xié)方差矩陣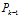 的條件下(初始值可以隨意取,但協(xié)方差矩陣應(yīng)為非0矩陣),則有
的條件下(初始值可以隨意取,但協(xié)方差矩陣應(yīng)為非0矩陣),則有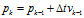 ,
,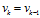 ,即:
,即:
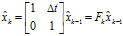
而此時(shí),
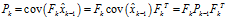
如果我們加入額外的控制量,比如加速度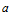 ,此時(shí)
,此時(shí)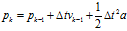 ,
,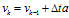 ,則此時(shí):
,則此時(shí):
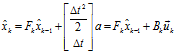
同時(shí),我們認(rèn)為我們對系統(tǒng)的估計(jì)值并非完全準(zhǔn)確,比如運(yùn)動(dòng)物體會突然打滑之類的,即存在一個(gè)協(xié)方差為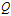 的噪聲干擾。因此,我們需要對
的噪聲干擾。因此,我們需要對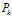 加上系統(tǒng)噪聲
加上系統(tǒng)噪聲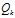 來保證描述的完備性。綜上,預(yù)測步驟的表達(dá)如下所示:
來保證描述的完備性。綜上,預(yù)測步驟的表達(dá)如下所示:
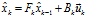
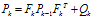
由于誤差累積的作用,單純對系統(tǒng)進(jìn)行估計(jì)會導(dǎo)致估計(jì)值越來越離譜,因此我們以傳感器的觀測數(shù)據(jù)對我們的估計(jì)進(jìn)行修正。我們可以用與預(yù)測步驟類似的方法將估計(jì)值空間映射至觀測值空間,如下式所示:
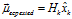
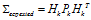
我們假設(shè)觀測值為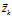 。同時(shí)由于觀測數(shù)據(jù)同樣會存在噪聲干擾問題,比如傳感器噪聲等,我們將這種噪聲的分布用協(xié)方差
。同時(shí)由于觀測數(shù)據(jù)同樣會存在噪聲干擾問題,比如傳感器噪聲等,我們將這種噪聲的分布用協(xié)方差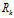 表示。此時(shí),觀測值
表示。此時(shí),觀測值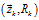 與估計(jì)值
與估計(jì)值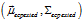 處于相同的狀態(tài)空間,但具有不同的概率分布,如圖2所示:
處于相同的狀態(tài)空間,但具有不同的概率分布,如圖2所示:
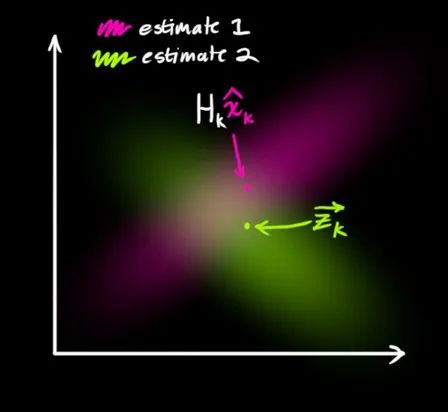
圖2 估計(jì)值與觀測值概率分布示意圖
我們可以認(rèn)為,這兩個(gè)概率分布的重疊部分,會更加趨近系統(tǒng)的真實(shí)數(shù)據(jù),即有更高的置信度,比如我們估計(jì)汽車速度是5~10km/h,傳感器反饋的速度是8~12km/h,那我們有理由認(rèn)為汽車的實(shí)際速度更趨近于8~10km/h這個(gè)區(qū)間。
這里將觀測值與估計(jì)值兩個(gè)分布的高斯分布相乘,其結(jié)果的高斯分布描述如下:
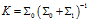
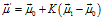 ? ? ??
? ? ??
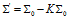
式中: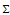 描述高斯分布的協(xié)方差,
描述高斯分布的協(xié)方差,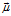 表示高斯分布的均值,矩陣
表示高斯分布的均值,矩陣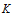 稱為卡爾曼增益矩陣。
稱為卡爾曼增益矩陣。
那么,將估計(jì)值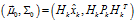 以及觀測值
以及觀測值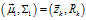 代入式(8)至式(10),可以得到:
代入式(8)至式(10),可以得到:
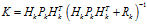
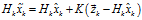
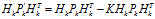
式中,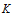 稱為卡爾曼增益。
稱為卡爾曼增益。
將式(11)至式(13)中約去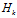 ,并化簡可得:
,并化簡可得:
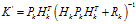
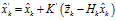
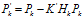
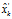 即為我們所得到的最優(yōu)估計(jì)值,同時(shí)
即為我們所得到的最優(yōu)估計(jì)值,同時(shí)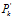 為其對應(yīng)的協(xié)方差矩陣。在實(shí)際應(yīng)用中,只需要使用式(4)、式(5)以及式(14)至式(16)這5個(gè)方程即可實(shí)現(xiàn)完整的卡爾曼濾波過程。
為其對應(yīng)的協(xié)方差矩陣。在實(shí)際應(yīng)用中,只需要使用式(4)、式(5)以及式(14)至式(16)這5個(gè)方程即可實(shí)現(xiàn)完整的卡爾曼濾波過程。
在對單一信號源濾波的場合,由于測量值與估計(jì)值具備幾乎完全相同的概率分布,為了更好的實(shí)現(xiàn)去噪效果,在假定被測對象變化不顯著的情況下,可以將之前(1~N)個(gè)時(shí)間節(jié)點(diǎn)的測量值隨機(jī)作為當(dāng)前時(shí)間節(jié)點(diǎn)的測量值,以實(shí)現(xiàn)更好的去噪效果。原則上,N取值越大濾波效果越好,但也會導(dǎo)致濾波結(jié)果滯后越嚴(yán)重。
2. 算法實(shí)現(xiàn)
function output = kalmanFilter(data, Q, R, N) if ~exist('Q', 'var') Q = 0.01; end if ~exist('R', 'var') R = 1; end if ~exist('N', 'var') N = 0; end X = 0; P = 1; A = 1; H = 1; output = zeros(size(data)); for ii = N + 1 : length(data) X_k = A * X; P_k = A * P * A' + Q; Kg = P_k * H' / (H * P_k * H' + R); z_k = data(ii - round(rand() * N)); X = X_k + Kg * (z_k - H * X_k); P = (1 - Kg*H) * P_k; output(ii) = X; end end
3. 算法分析
采用經(jīng)典卡爾曼濾波對虛擬信號及真實(shí)信號進(jìn)行濾波,結(jié)果如下圖所示:
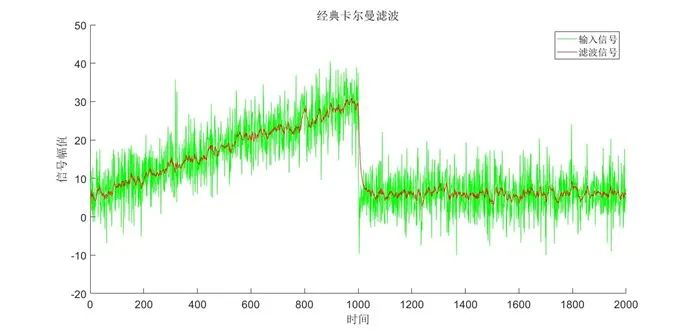
圖3 經(jīng)典卡爾曼濾波對虛擬信號濾波結(jié)果
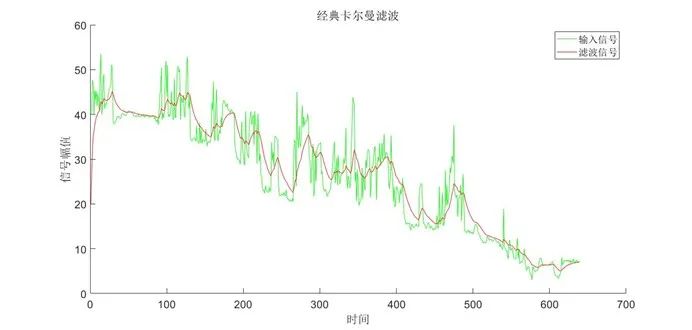
圖4 經(jīng)典卡爾曼濾波對真實(shí)信號濾波結(jié)果
從濾波結(jié)果中可以看出,經(jīng)典卡爾曼對信號的濾波效果較為優(yōu)秀,實(shí)時(shí)性相對較好,計(jì)算量需求極小,能夠有效去除高斯噪聲以及非高斯噪聲,基本不受脈沖信號影響。在對被測系統(tǒng)的建模較為精確的條件下,其性能還能夠進(jìn)一步提升。其缺點(diǎn)主要在于需人為給定系統(tǒng)模型,當(dāng)系統(tǒng)模型不精確時(shí)濾波效果會有所下降,但可以通過增加采樣頻率解決此問題。
建議應(yīng)用場合:輸入信號相對平穩(wěn)或已知被測系統(tǒng)運(yùn)動(dòng)學(xué)模型,同時(shí)要求運(yùn)算量極小的場合。
責(zé)任編輯:xj
原文標(biāo)題:濾波算法:經(jīng)典卡爾曼濾波
文章出處:【微信公眾號:FPGA之家】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
-
濾波
+關(guān)注
關(guān)注
10文章
667瀏覽量
56646 -
算法
+關(guān)注
關(guān)注
23文章
4612瀏覽量
92891 -
卡爾曼濾波
+關(guān)注
關(guān)注
3文章
165瀏覽量
24650
原文標(biāo)題:濾波算法:經(jīng)典卡爾曼濾波
文章出處:【微信號:zhuyandz,微信公眾號:FPGA之家】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
卡爾曼濾波在信號處理中的應(yīng)用分析
卡爾曼濾波在圖像處理中的應(yīng)用實(shí)例 如何調(diào)優(yōu)卡爾曼濾波參數(shù)
【「從算法到電路—數(shù)字芯片算法的電路實(shí)現(xiàn)」閱讀體驗(yàn)】+閱讀濾波器章節(jié)部分筆記
經(jīng)典濾波器的設(shè)計(jì)說明
卡爾曼濾波器的特性及仿真

常用的ADC濾波算法有哪些
從算法角度看 SLAM(第 2 部分)

貝葉斯濾波和卡爾曼濾波的區(qū)別
卡爾曼濾波的優(yōu)缺點(diǎn)有哪些
卡爾曼濾波是什么 卡爾曼濾波與目標(biāo)追蹤技術(shù)分析





 經(jīng)典卡爾曼濾波算法步驟
經(jīng)典卡爾曼濾波算法步驟
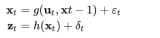










評論