一、卡爾曼濾波介紹
1.1 卡爾曼濾波是什么
本節為卡爾曼濾波,主要講解卡爾曼濾波的具體推導,卡爾曼濾波在行人狀態估計中的一個小例子。
我們通常要對一些事物的狀態去做估計,為什么要做估計呢?因為我們通常無法精確的知道物體當前的狀態。為了估計一個事物的狀態,我們往往會去測量它,但是我們不能完全相信我們的測量,因為我們的測量是不精準的,它往往會存在一定的噪聲,這個時候我們就要去估計我們的狀態。卡爾曼濾波就是一種結合預測(先驗分布)和測量更新(似然)的狀態估計算法。
1.2 為什么要學卡爾曼濾波
卡爾曼濾波以及其擴展算法能夠應用于目標狀態估計,如果這個目標是行人,那么就是行人狀態估計(或者說行人追蹤),如果這個目標是自身,那么就是車輛自身的追蹤(結合一些地圖的先驗,GPS等數據的話就是自身的定位)。在很多的無人駕駛汽車項目中,都能找到卡爾曼濾波的擴展算法的身影(比如說EKF,UKF等等)。本節我們從最簡單的卡爾曼濾波出發,完整的理解一遍卡爾曼濾波的推導過程,并實現一個簡單的狀態估計Python程序。
1.3為什么會叫濾波算法
以一維卡爾曼濾波為例,如果我們單純的相信測量的信號,那么這個信號是包含噪聲的,是很毛糙的,但是當我們運行卡爾曼濾波算法去做估計,我們估計的信號會很光滑,看起來似乎濾掉了噪聲的影響,所以稱之為濾波算法。實際上,卡爾曼濾波不僅僅過濾掉了測量信號的噪聲,它同時也結合了以往的估計,卡爾曼濾波在線性問題中被證明是最優估計。
1.4一些概率論的基礎知識
下面是一些概率論的基礎知識,如果之前有這方面的知識儲備那當然是最好的,很有利于我們理解整個博客內容,如果沒有這方面的基礎而且也看不懂下面的內容也沒關系,我會以一個相對直觀的方式來展現整個理論部分。
先驗概率 P (X):僅僅依賴主觀上的經驗,事先根據已有的只是的推斷
后驗概率 P (X∣Z):是在相關證據或者背景給定并納入考慮以后的條件概率
似然 P (Z∣X):已知結果區推測固有性質的可能性
貝葉斯公式:
后驗分布正比于先驗分布乘以似然。
二、卡爾曼濾波的完整推導
2.1 一個簡單例子
若干年后,我們的可回收火箭要降落到地球,我們比較關心的狀態就是我們的飛行器的高度了,飛行器的高度就是我們想要估計的狀態,我們會通過一些傳感器去測量我們當前的高度信息,比如說使用氣壓計。假如我們每一次測量,當前高度都變成上一次測量的95%,那么我們就可以得到如下關系:
我們可以使用遞歸來表示這樣的公式——為了計算我們當前的高度,我們必須知道我們上一個測量的高度,以此遞推,我們就會推到我們的飛行器的初始高度。
但是,由于我們的測量往往來自于一些傳感器(比如說GPS,氣壓計),所以測量的結果總是帶有噪聲的,這個噪聲是由傳感器本身引起的,那么我們的表達式就變成了:
這個噪聲我們稱之為測量噪聲 (Measurement Noise)。通常來說,這種噪聲都滿足高斯分布。我們用符號描述以上兩部分:
第一個式子是我們的過程模型,是我們的經驗(比如說一些運動模型,牛頓力學等等),我們用這種過程模型去 預測 我們考察的事物狀態(在沒有任何信息的情況下,或者說在沒有任何測量數據的情況下);第二個式子是測量的表達式,它大致描述了我們測量的組成成分,我們用這個測量去更新我們對狀態的估計。其中是我們的飛行器當前的狀態,是我們上一個狀態(注意狀態和測量的區別),是我們當前對飛行器的測量,是我們當前的測量噪聲, a是一個常數,在我們這個例子里面就是 0.95。
思考一下,在這里我們用一個簡單的比例(常數)來描述“可回收火箭”的運動規律,會存在什么問題?
很顯然,現實中的運動不會像我們這個簡單的過程模型一樣高度按比例縮小。在這里為了簡化,我們先假設我們的模型挺好的,能夠大致描述出這顆“神奇火箭”的運動規律,只是偶爾會存在一定的偏差(比如所空氣湍流的影響),那么我們在計算時再加一個噪聲來描述我們的過程模型與實際運動的差異,這個噪聲我們稱之為過程噪聲 (Process Noise),我們用來表示這種噪聲,那么 的計算公式就變成:
為了簡化,后面的分析我們會先忽略過程噪聲,但是我們在傳感器融合的部分會將過程噪聲重新考慮進來。
2.2 狀態估計
因為我們是要估計飛行器的狀態(高度),所以我們把測量的公式變換成:
顯然,在這里是沒辦法知道的,卡爾曼濾波通過同時考慮上一狀態值和當前的測量值來獲得對當前狀態值的估計。一般我們用 來表示對狀態 x 的估計。那么 就表示當前狀態的估計。下面我們可以用如下公式來描述卡爾曼濾波如何結合上一個估計和和現在的測量來產生對當前的估計: 這里的叫做 卡爾曼增益(Kalman Gain),它描述的是之前的估計和當前的測量對當前的估計的影響的分配權重。為了理解,我們考慮極端的例子,如果 也就是說增益為 0,那么: 也就是說我們非常不信任我們當前的測量,我們直接保留了我們上一次的估計作為我們對當前狀態的估計。如果 ,即增益為 1,則: 即我認為當前的測量非常可信,我徹底接受它作為我當前狀態的估計。那么當介于 ( 0 , 1 ) ,則表示對兩者的權重分配。
2.3計算卡爾曼增益
那么如何計算卡爾曼增益呢?我們使用一種間接的方法,我們雖然不知道測量噪聲 的值,但是我們知道它的均值,前面我們提到,測量噪聲來自傳感器本身,并且符合高斯分布,所以我們能夠從傳感器廠商那里獲得測量噪聲的均值 ,那么 可以表示為: 其中叫預測誤差,表達式為: 那么怎么理解和 呢?假設前一次的預測誤差,那么根據公式,當前的增益,一維則舍棄掉當前的測量而完全采用上一個時刻的估計,如果,那么增益變成 通常 是個很小的數值,所以增益為1,所以完全接受這一次的測量作為我們的估計(因為上一次的的預測誤差太大了,為1,所以一旦拿到了新的測量,如獲至寶,就干脆把不準確的上次的估計舍棄掉了) 對于下面的公式的分析是一樣的,我們考慮極端的例子,當增益為 0 ,,因為我們徹底舍棄掉了本次的測量,所以本次的預測誤差只能接受上一次的。當增益為 1 ,
2.4預測和更新
那么現在我們有關于當前的火箭高度狀態的兩個公式了,它們分別是:
那么我們到底要用哪一個呢?答案是我們都用,第一個公式我們稱之為預測,是基于一些先驗的知識(比如說運動模型,牛頓力學等等)覺得我們的狀態應該是這樣的,而第二個公式呢,就是我們基于我們“不完美的”的傳感器的測量數據來更新我們對狀態的估計。另外,預測,理論上只考慮了一個固定的過程模型和過程噪聲,但是由于我們現在是對機械的狀態進行估計,在預測過程中需要對機械本身的控制建模, 我們在預測部分再新增一個控制信號,我們用表示。實際的傳感器測量除了會有測量噪聲 以外,還會存在一定的關于真實狀態的縮放,因此我們使用 表示測量時通常還會在其前面加一個縮放系數。結合這些我們就可以得到卡爾曼濾波預測和更新過程了: 預測 卡爾曼濾波更新的過程為: 使用線性代數的方法來表示預測和更新 預測 卡爾曼濾波更新的過程為: 至此,卡爾曼濾波的完整推導就結束了。下面,我們來看看卡爾曼濾波在無人汽車的感知模塊的應用。
三、卡爾曼濾波在無人駕駛感知模塊的應用
3.1無人車感知模塊的傳感器
無人駕駛汽車要安全的在道路上行駛,需要“耳聽六路,眼觀八方”。那么無人車的耳朵和眼睛是什么呢?那就是安裝在無人車上的各種各樣的傳感器了。無人車上的傳感器能夠多達幾十個,而且是不同種類的,比如:
立體攝像機
交通標志攝像機
雷達(RADAR)
激光雷達(LIDAR)立體攝像機往往用于獲取圖像和距離信息;交通標志攝像機用于交通標志的識別;雷達一般安裝在車輛的前保險桿里面,用于測量相對于車輛坐標系下的物體,可以用來定位,測距,測速等等,容易受強反射物體的干擾,通常不用于靜止物體的檢測;激光雷達往往安裝在車頂,使用紅外激光束來獲得物體的距離和位置,但是空間分辨率高,但是笨重,容易被天氣影響。
由此可知,各種傳感器都有其優點和缺點,在實際的無人駕駛汽車里,我們往往結合多種傳感器的數據去感知我們的車輛周邊的環境。這種結合各種傳感器的測量數據的過程我們稱之為傳感器融合(Sensor Fusion)。本系列博客后面的章節我將詳細給大家介紹基于擴展卡爾曼濾波和無損卡爾曼濾波在傳感器融合中的應用。在本節中,我們主要考慮卡爾曼濾波基于單一的傳感器數據來估算行人位置的方法。
3.2基于卡爾曼濾波的行人位置估算
卡爾曼濾波雖然簡單,確實無人駕駛汽車的技術樹中非常重要的一部分,當然,在真實的無人駕駛汽車項目中使用到的技術是相對更加復雜的,但是其基本原理仍然是本博客介紹的這些內容。在無人駕駛中,卡爾曼濾波主要可以用于一些狀態的估計,主要應用于行人,自行車以及其他汽車的狀態估計。下面,我們以行人的狀態估計為例展開。當我們要估計一個行人的狀態時,首先就是要建立起腰估計的狀態的表示。這里,行人的狀態大致可以表示為, 其中為行人的位置,而則是行人此時的速度。我們用一個向量來表示一個狀態: 在確定了我們要估計的狀態以后,我們需要確定一個過程模型,如前文所說,過程模型用于預測階段來產生一個對當前估計的先驗。在本文中,我們先以一個最簡單的過程模型來描述行人的運動——恒定速度模型: 即:
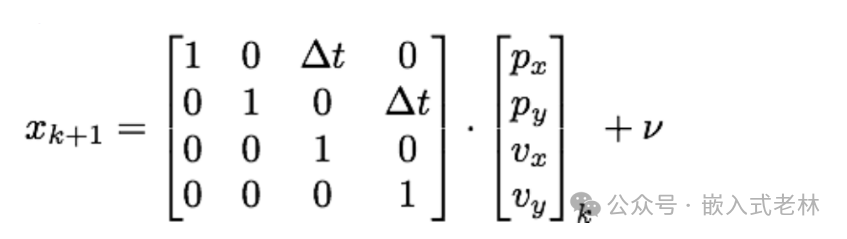
之所以稱之為恒定速度模型,是因為我們將上面這個行列式展開可以得到:
恒定速度過程模型假定預測的目標的運動規律是恒定的速度的,在行人狀態預測這個問題中,很顯然行人并不一定會以恒定的速度運動,所以我們的過程模型包含了一定的 過程噪聲,在這個問題中過程噪聲也被考慮了進來,其中的是我們這個過程模型的過程噪聲。在行人狀態估計中的過程噪聲其實就是行人的加減速,那么我們原來的處理過程就變成了:
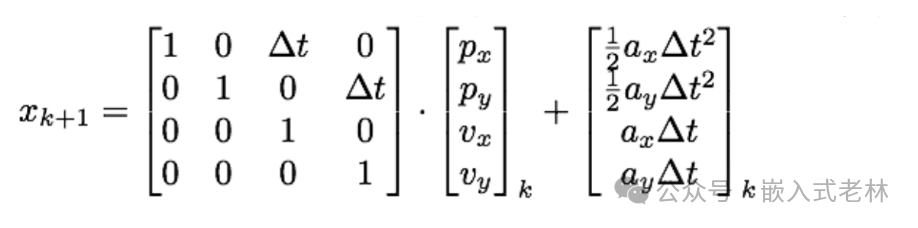
我們預測的第二步就變成了:
這就是的更新過程,它本質上是我們的估計狀態概率分布的協方差矩陣。是我們的過程噪聲的協方差矩陣,由于過程噪聲是隨機帶入的,所以本質是一個高斯分布:, 是過程噪聲的協方差, 的形式為:
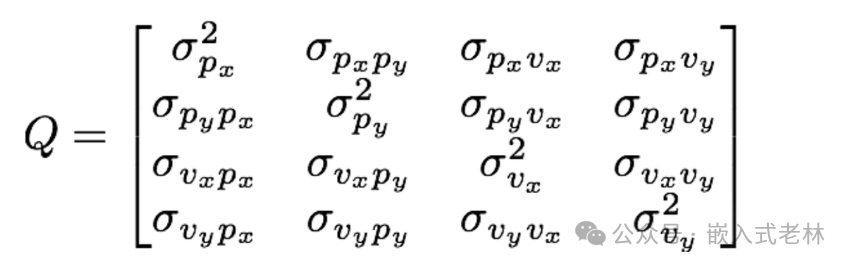
進而表示為:
其中, 對于行人我們可以設置為(這一部分大家如果想要詳細了解可以閱讀這篇文章:http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=5940526)。
測量步驟中,我們直接可以測量到速度和,所以我們的測量矩陣可以表示為:

測量噪聲的協方差矩陣 為:
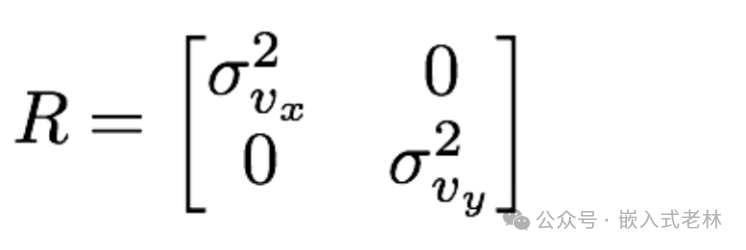
其中的 和 描述了我們的傳感器的測量能夠有多“差”,這是傳感器固有的性質,所以往往是傳感器廠商提供。
最后,在測量的最后一步,我們使用單位矩陣來代替原式中的1:
至此,基于恒定速度過程模型卡爾曼濾波的行人狀態估計的整個流程我們就講完了,下面我們使用Python將整個過程實現一下。
四、卡爾曼濾波在行人狀態估計中的Python例子
首先我們看一下卡爾曼濾波的整個流程,其實在實際的論文和資料中,預測矩陣通常使用來表示(我們前文中一直是使用),測量矩陣通常使用 表示(我們前文中使用的是),卡爾曼增益通常使用來表示(我們前文中使用的是),下面是文獻材料中通常意義的卡爾曼濾波過程:
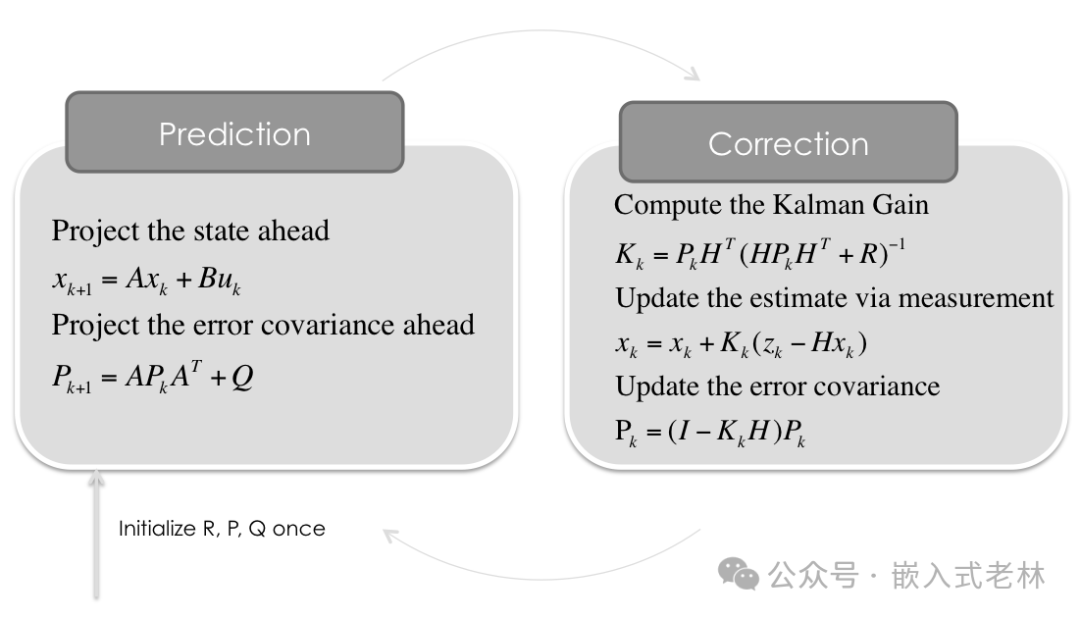
注意:公式還包含一項: ,這一項是指我們在追蹤一個物體的狀態的時候把它內部的控制也考慮進去了,這在行人,自行車,其他汽車的狀態估計問題中是無法測量的,所以在這個問題中我們設置 為 0 .
我們的代碼將在IPython中執行,大家可以在jupyter notebook中交互式地運行。
首先我們載入必要的庫:
import numpy as np %matplotlib inline import matplotlib.pyplot as plt fromscipy.statsimportnorm
接著我們初始化行人狀態x, 行人的不確定性(協方差矩陣)P,測量的時間間隔dt,處理矩陣F以及測量矩陣H:
x = np.matrix([[0.0, 0.0, 0.0, 0.0]]).T
print(x, x.shape)
P = np.diag([1000.0, 1000.0, 1000.0, 1000.0])
print(P, P.shape)
dt = 0.1 # Time Step between Filter Steps
F = np.matrix([[1.0, 0.0, dt, 0.0],
[0.0, 1.0, 0.0, dt],
[0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 1.0]])
print(F, F.shape)
H = np.matrix([[0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 1.0]])
print(H, H.shape)
ra = 10.0**2
R = np.matrix([[ra, 0.0],
[0.0, ra]])
print(R,R.shape)
計算測量過程的噪聲的協方差矩陣R和過程噪聲的協方差矩陣Q:
ra = 0.09
R = np.matrix([[ra, 0.0],
[0.0, ra]])
print(R, R.shape)
sv = 0.5
G = np.matrix([[0.5*dt**2],
[0.5*dt**2],
[dt],
[dt]])
Q = G*G.T*sv**2
from sympy import Symbol, Matrix
from sympy.interactive import printing
printing.init_printing()
dts = Symbol('dt')
Qs = Matrix([[0.5*dts**2],[0.5*dts**2],[dts],[dts]])
Qs*Qs.T
定義一個單位矩陣:
I = np.eye(4) print(I,I.shape)
我們隨機產生一些測量數據:
m = 200 # Measurements
vx= 20 # in X
vy= 10 # in Y
mx = np.array(vx+np.random.randn(m))
my = np.array(vy+np.random.randn(m))
measurements = np.vstack((mx,my))
print(measurements.shape)
print('Standard Deviation of Acceleration Measurements=%.2f' % np.std(mx))
print('You assumed %.2f in R.' % R[0,0])
fig = plt.figure(figsize=(16,5))
plt.step(range(m),mx, label='$dot x$')
plt.step(range(m),my, label='$dot y$')
plt.ylabel(r'Velocity $m/s$')
plt.title('Measurements')
plt.legend(loc='best',prop={'size':18})
一些過程值,用于結果的顯示:
xt = []
yt = []
dxt= []
dyt= []
Zx = []
Zy = []
Px = []
Py = []
Pdx= []
Pdy= []
Rdx= []
Rdy= []
Kx = []
Ky = []
Kdx= []
Kdy= []
def savestates(x, Z, P, R, K):
xt.append(float(x[0]))
yt.append(float(x[1]))
dxt.append(float(x[2]))
dyt.append(float(x[3]))
Zx.append(float(Z[0]))
Zy.append(float(Z[1]))
Px.append(float(P[0,0]))
Py.append(float(P[1,1]))
Pdx.append(float(P[2,2]))
Pdy.append(float(P[3,3]))
Rdx.append(float(R[0,0]))
Rdy.append(float(R[1,1]))
Kx.append(float(K[0,0]))
Ky.append(float(K[1,0]))
Kdx.append(float(K[2,0]))
Kdy.append(float(K[3,0]))
卡爾曼濾波:
for n in range(len(measurements[0])):
# Time Update (Prediction)
# ========================
# Project the state ahead
x = F*x
# Project the error covariance ahead
P = F*P*F.T + Q
# Measurement Update (Correction)
# ===============================
# Compute the Kalman Gain
S = H*P*H.T + R
K = (P*H.T) * np.linalg.pinv(S)
# Update the estimate via z
Z = measurements[:,n].reshape(2,1)
y = Z - (H*x) # Innovation or Residual
x = x + (K*y)
# Update the error covariance
P = (I - (K*H))*P
# Save states (for Plotting)
savestates(x,Z,P,R,K)
顯示一下關于速度的估計結果:
def plot_x():
fig = plt.figure(figsize=(16,9))
plt.step(range(len(measurements[0])),dxt, label='$estimateVx$')
plt.step(range(len(measurements[0])),dyt, label='$estimateVy$')
plt.step(range(len(measurements[0])),measurements[0], label='$measurementVx$')
plt.step(range(len(measurements[0])),measurements[1], label='$measurementVy$')
plt.axhline(vx, color='#999999', label='$trueVx$')
plt.axhline(vy, color='#999999', label='$trueVy$')
plt.xlabel('Filter Step')
plt.title('Estimate (Elements from State Vector $x$)')
plt.legend(loc='best',prop={'size':11})
plt.ylim([0, 30])
plt.ylabel('Velocity')
plot_x()
預測的結果如圖所示:
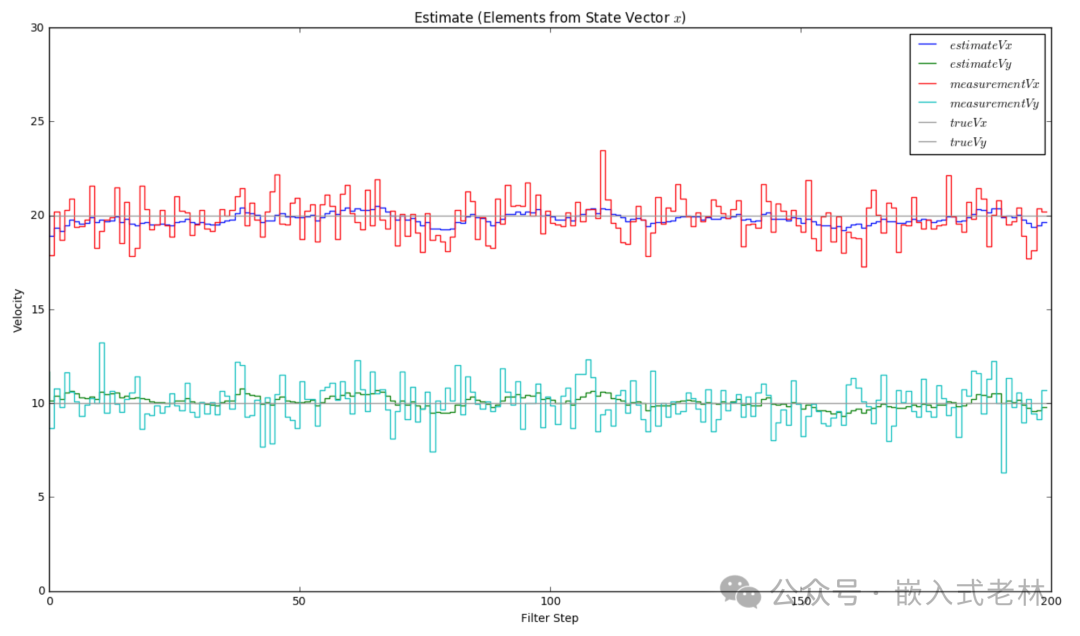
位置的估計結果:
def plot_xy():
fig = plt.figure(figsize=(16,16))
plt.scatter(xt,yt, s=20, label='State', c='k')
plt.scatter(xt[0],yt[0], s=100, label='Start', c='g')
plt.scatter(xt[-1],yt[-1], s=100, label='Goal', c='r')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Position')
plt.legend(loc='best')
plt.axis('equal')
plot_xy()
預測的結果如圖所示:
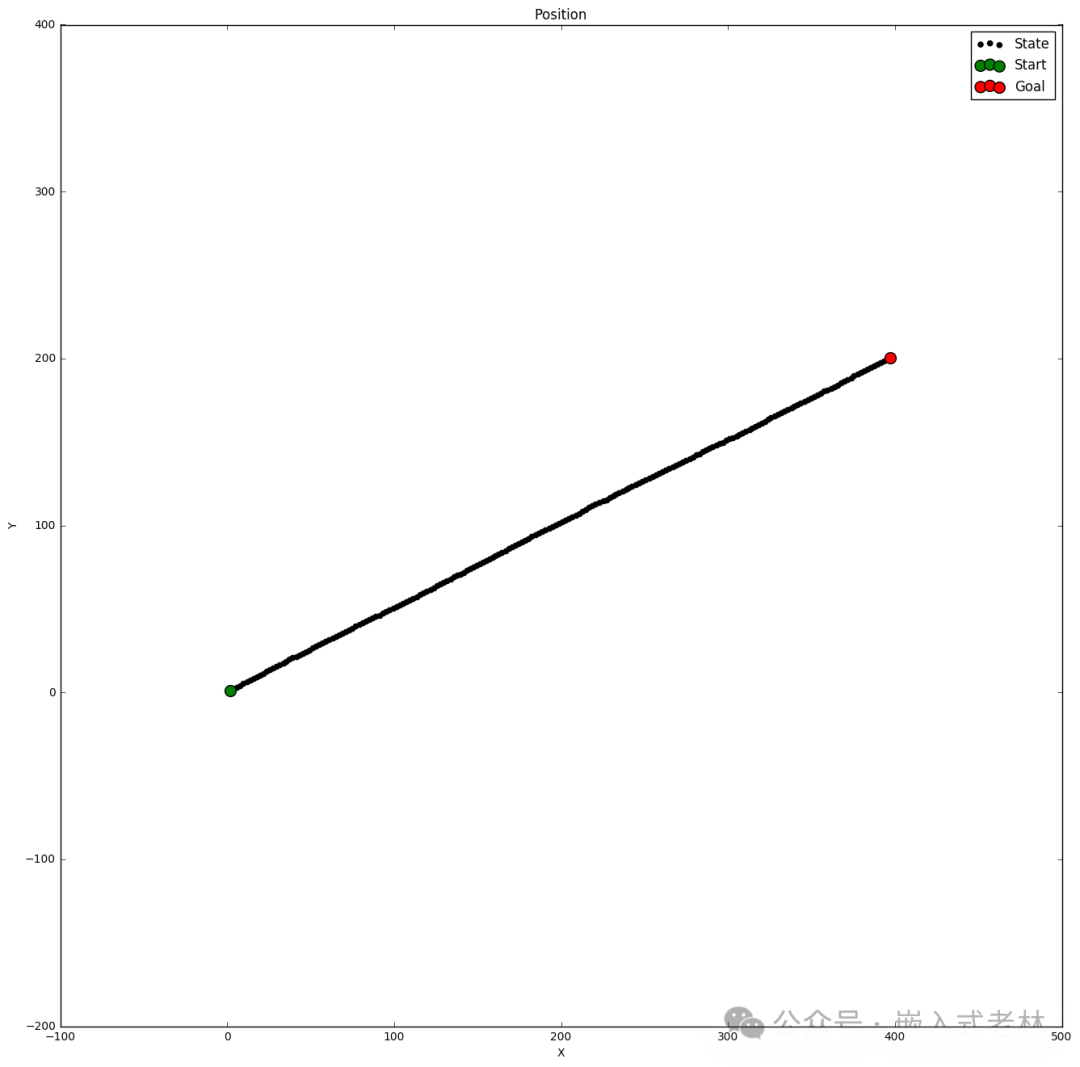
雖然本例中以無人駕駛的行人檢測作為落腳點講解卡爾曼濾波,但是實際上我們的無人車并不會僅僅使用原始的卡爾曼濾波作為行人感知的狀態估計,因為卡爾曼濾波存在著一個非常大的局限性——它僅能對線性的過程模型和測量模型進行精確的估計,在非線性的場景中并不能達到最優的估計效果,為了能夠設定線性的環境,我們假定了我們的過程模型為恒定速度模型,但是顯然在顯示的應用中不是這樣的,不論是過程模型還是測量模型,都是非線性的,下一篇我將介紹一種能夠應用于非線性情況的卡爾曼濾波算法——擴展卡爾曼濾波。
審核編輯:黃飛
-
傳感器
+關注
關注
2564文章
52706瀏覽量
764639 -
gps
+關注
關注
22文章
2971瀏覽量
168679 -
飛行器
+關注
關注
13文章
739瀏覽量
46231 -
卡爾曼濾波
+關注
關注
3文章
166瀏覽量
25015
原文標題:卡爾曼濾波與目標追蹤
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄





 卡爾曼濾波是什么 卡爾曼濾波與目標追蹤技術分析
卡爾曼濾波是什么 卡爾曼濾波與目標追蹤技術分析
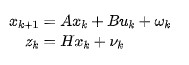
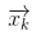
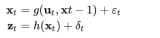










評論