真值與機器值

真值很好理解，就是十進制的數字前面再加上正負號，這是人類可以簡單識別的數字，比如 0、±16、±1084、±10.34、±100.453 等，而正數前面的+符號可以省略。機器值從字面理解就是機器（計算機）識別的值，實際上也確實是這個意思。

計算機中通過高低電平表示1或者0，這樣就可以表示一個二進制的數值。一個1或者0表示的數值位稱為一個bit，而計算機中存儲和傳輸數據的最小單位是一個字節（byte）也就是8個bit，所以說計算機所有計算本質上都是基于二進制。

在計算機中，我們可以使用1個或者多個字節存儲一個數，但無論是多少個字節，其大小肯定是固定的，同時其所能表示的數值的范圍也是固定的。比如說對使用1個字節存儲的數進行計算或者傳輸，那么這個數所能表示的最小值為00000000最大值為11111111，轉換為十進制為0 ~ 255。那么無論對這個數做了什么計算，無論計算之后的結果為多少都不能超出這個范圍，同理使用2個字節存儲的數范圍為0 ~ 65535。

由于很多時候一個數據需要使用2個或者2個以上的字節表示，那么這種數據無論是存儲還是傳輸的時候都會有一個順序的問題，也就是大小端對齊（字節序）問題。在存儲時高位字節在前為大端對齊，反之為小端對齊。在數據傳輸時先傳輸高位字節為大端字節序，反之為小端字節序。目前絕大多數平臺內部都是小端對齊的方式存儲數據，而大多數通信協議卻都是用大端字節序傳輸數據，所以這一點值得注意一下。

符號位與數值位

計算機中使用二進制存儲傳輸和計算數值，但是不能只有數值，計算的時候還得有正負之分。在計算機中使用最高bit位的數值來表示正負號，這個bit位稱作符號位。

計算機中符號位的值為0表示這個數為正數，符號位值為1表示這個樹為負數。由于符號位表示符號所以其不表示具體的值，除開符號位剩余的bit位用來表示數值也就是數值位。比如1個字節的整數00000001，其中最高bit（最左邊）位的0為符號位，表示這個數為正數，數值位為1，所以其真值為1。同理2個字節的整數00000000_0000001，其真值也是1。

原碼、反碼和補碼

計算機只識別機器碼，其實也就是二進制數，并且使用最高bit位表示符號位。那么兩個真值為8和-8的8位整數，它們在計算機內部的機器值是否就分別是00001000和10001000？其實并不是，這只是8和-8的原碼，而機器算計中的機器值是使用補碼存儲和計算的。

計算機中，正數的原碼、反碼和補碼是一樣的，所以上面那個例子中，真值為8的8位整數的機器值確實是00001000，但是-8就不是這么回事了。負數的首先將原碼數值位按位取反得到反碼，然后再將反碼數值位加1之后則得到補碼。我們來看一下-8這個例子，其原碼為10001000，數值位按位取反之后的反碼為11110111，然后數值位加1之后的補碼為11111000。所以真值為-8的8位整數在計算機中的機器值為11111000，我們來看下面這張表：

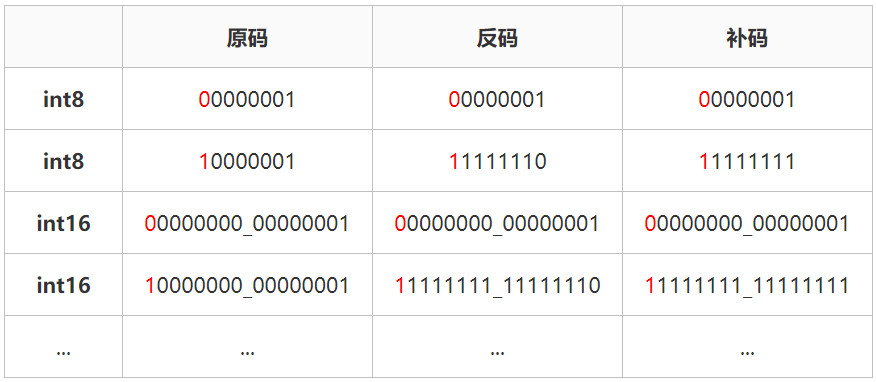
注：int8為8bit位整數占用1byte，int16為16bit位整數占用2byte。

剛說的是原碼轉補碼的步驟，其實補碼轉原碼的步驟是一樣的。首先正數的原碼補碼是一樣的不需要轉換，我們看負數11111000，首先將數值位按位取反得到10000111，然后再將數值位加1得到10001000。我們再來看一個8位的整數10000000，是不是發現這個數原碼和補碼是一樣的，那么這個看起來像是“-0”的數是怎么回事呢？其實可以將這個數看成是一個特殊值，它的真實含義就是最小值。8位的這種“-0”的真值為-128，16位的這種“-0”真值為-32768。所以只需要記住100...000這種補碼就是最小值就行，我們看下面的這張表：

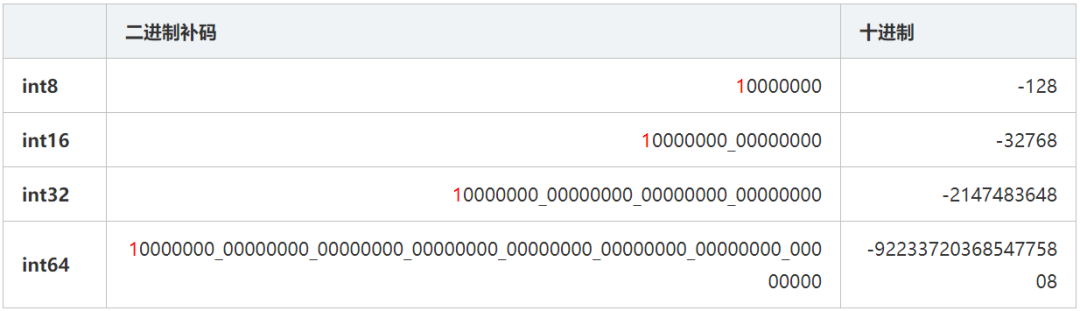
有兩對8bit位的整數4、8和4、-8，我們分別看一下他們在計算機中是怎么做加法計算的。首先看4和8的補碼分別為00000100和00001000，只需要將每個bit位相加就行，結果為00001100，其真值為12。我們再來4和-8的計算，它們補碼分別為00000100和11111000，然后將它們按位相加（注意符號位也要做加法）得到11111100，其原碼為10000100，真值為-4。

再來看一下減法計算，比如8bit位的整數-8減去4，首先可以將4處理一下可以變為(-8) + (-4)，這樣是不是就又變為了加法了？-8和-4的補碼分別為11111000和11111100，將它們按位相加得到補碼11110100（注意這是8位的整數，超出部分發生了溢出），轉換成原碼為10001100，真值為-12。

再來看一下乘法，比如8bit位的整數-8乘以13，他們的補碼分別為11111000和00001101。其中-8為被乘數，13為乘數，并且乘數有8個bit位，需要將被乘數按位與和位計算8次然后將結果相加，看如下分析：

被乘數的第0個bit位值為1，將被乘數乘以1然后左移0位得到：11111000；

被乘數的第1個bit位值為0，將被乘數乘以0然后左移1位得到：00000000；

被乘數的第2個bit位值為1，將被乘數乘以1然后左移2位得到；11100000；

被乘數的第3個bit位值為1，將被乘數乘以1然后左移3位得到；11000000；

被乘數的第4個bit位值為0，將被乘數乘以0然后左移4位得到；00000000；

被乘數的第5個bit位值為0，將被乘數乘以0然后左移5位得到；00000000；

被乘數的第6個bit位值為0，將被乘數乘以0然后左移6位得到；00000000；

被乘數的第7個bit位值為0，將被乘數乘以0然后左移7位得到；00000000；

由此可以得計算得到8組補碼（注意上面做位移涉及到的整數溢出，只能是8個bit位），然后將它們做加法得到10011000（也存在整數溢出）轉換為原碼為11101000，真值為-104。

至于除法則是使用交替加減法的方式，本文只是對計算原理做一下擴展，這里不再繼續深入做介紹，如果有想了解的可以自行上網查詢。

通過上面的分析可以知道，使用補碼可以將所有計算都轉化為加法計算，這樣可以讓計算機底層對于整數計算變得簡單，反碼屬于歷史遺留，因為其存在±0的問題。

原文標題：二進制原碼/反碼/補碼詳解，不懂的請看過來

文章出處：【微信公眾號：嵌入式ARM】歡迎添加關注！文章轉載請注明出處。

責任編輯：haq