注:本文是BAT真題收錄很值得大家花心思看完,看完會有收獲。
前言
算法是面試大公司必考的項目,所以面試前準備好算法至關重要,今天整理的常見的動態規劃題目,希望可以幫到大家。
要想學習其他絕世武功,要先打好基礎。算法屬于內功,則更為重要。
強盜搶劫
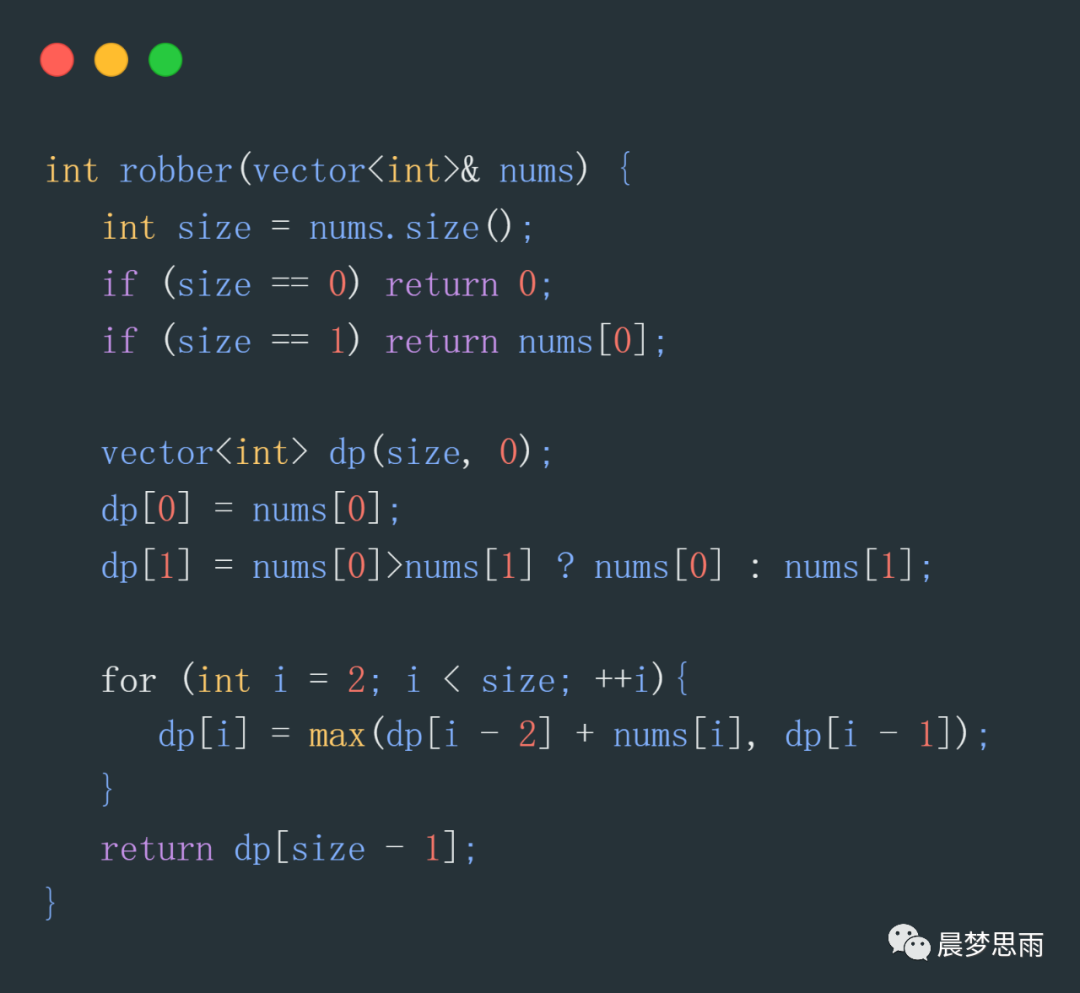
題目:強盜搶劫一排房間,每個房間都有錢,不能搶劫兩個相鄰的房間,要求搶的錢最多。數組如:[2,7,9,3,1]
思路:當輸入房間數為0,1,2時,這個很好判斷,當輸入房間數字大于3時,就要用到動態規劃了,方程是:

dp[i]是當搶到第i個數時,能搶到最大值,從局部最大值推到最終結果最大。
假如搶到第5個房間,那么第5個房間有二種情況,搶不和不被搶,因為只能隔房間。
如果搶到第4個房間,有個最大值;搶到第3個房間,有個最大值。
如果加上第3房間最大值,加上第5房間的最大值,大于搶到第4個房間時的最大時。那就搶3,5而不搶4,反而,就按搶4的策略。
這樣從前往后推,最后的結果一定是最大的。
代碼如下:
跳臺階
題目描述:有 N 階樓梯,每次可上一階或兩階,求有多少種上樓梯的方法
先來分析下這個問題:
當N=1時,這個很好理解,只能跨1步這一種了
當N=2時,你每次可以跨1步或2步,那就是走2步或走兩個1步
當N=3時,因為你可以跨1步或2步,那你在臺階1或2都能行。要計算到臺階1有多少種走法,到臺階2有多少種走法,然后2種相加,依次逆推。
當N=4時,你在臺階2或3都能行,計算到臺階2有多少種走法,到臺階3有多少種走法,然后2者相加,依次逆推。
總結如下:你會發現,這是斐波拉切數列,使用遞歸出現重復計算問題,所以選擇動態規劃算法。
| 層數 | 公式 | 種數 |
| 1 | f(1)=1 | 1 |
| 2 | f(2)=2 | 2 |
| 3 | f(3)=f(1)+f(2) | 3 |
| 4 | f(4)=f(2)+f(3) | 5 |
第三層:3種(在第一層走2步或在第二層走1步)
第四層:5種(在第二層走2步或在第三層走1步)

i,j首先賦邊界值,res保存i+j的值,每次前進,i,j,res的值都會被賦到前面結果。
上面的算法是底向上,遞歸相當于自頂向下,避免了重復計算。
矩形最小路徑和
題目:
給定一個,包含非負整數的 m x n 網格。請找出一條,從左上角到右下角的路徑。使得路徑上,所有數字總和為最小,每次只能向下,或者向右移動一步。
輸入:[[1,3,1],
[1,5,1],
[4,2,1]]
輸出: 7
解釋: 因為路徑 1→3→1→1→1 的總和最小。
先看動態方程:
| i值 | j值 | dp方程 |
| i>0 | j=0 | dp[i][0] = dp[i?1][0] + grid[i][0] |
| i=0 | j>0 | dp[0][j] = dp[0][j?1] + grid[0][j] |
| i>0 | j>0 | dp[i][j] = min(dp[i?1][j], dp[i][j?1]) + grid[i][j] |
說明:因為 i=0 和 j=0 是臨界條件,所以要先求出來。當 i>0 和 j>0 時,看如上數組,5 可以由上方3,或者左方 1 走過來。
當走5的時候,要選取上方3對應的dp,與左方1 對應的dp進行比較,選擇較小值累加,這樣走出來的才是最小值。最后推出,到右下角的最小值。
代碼如下:
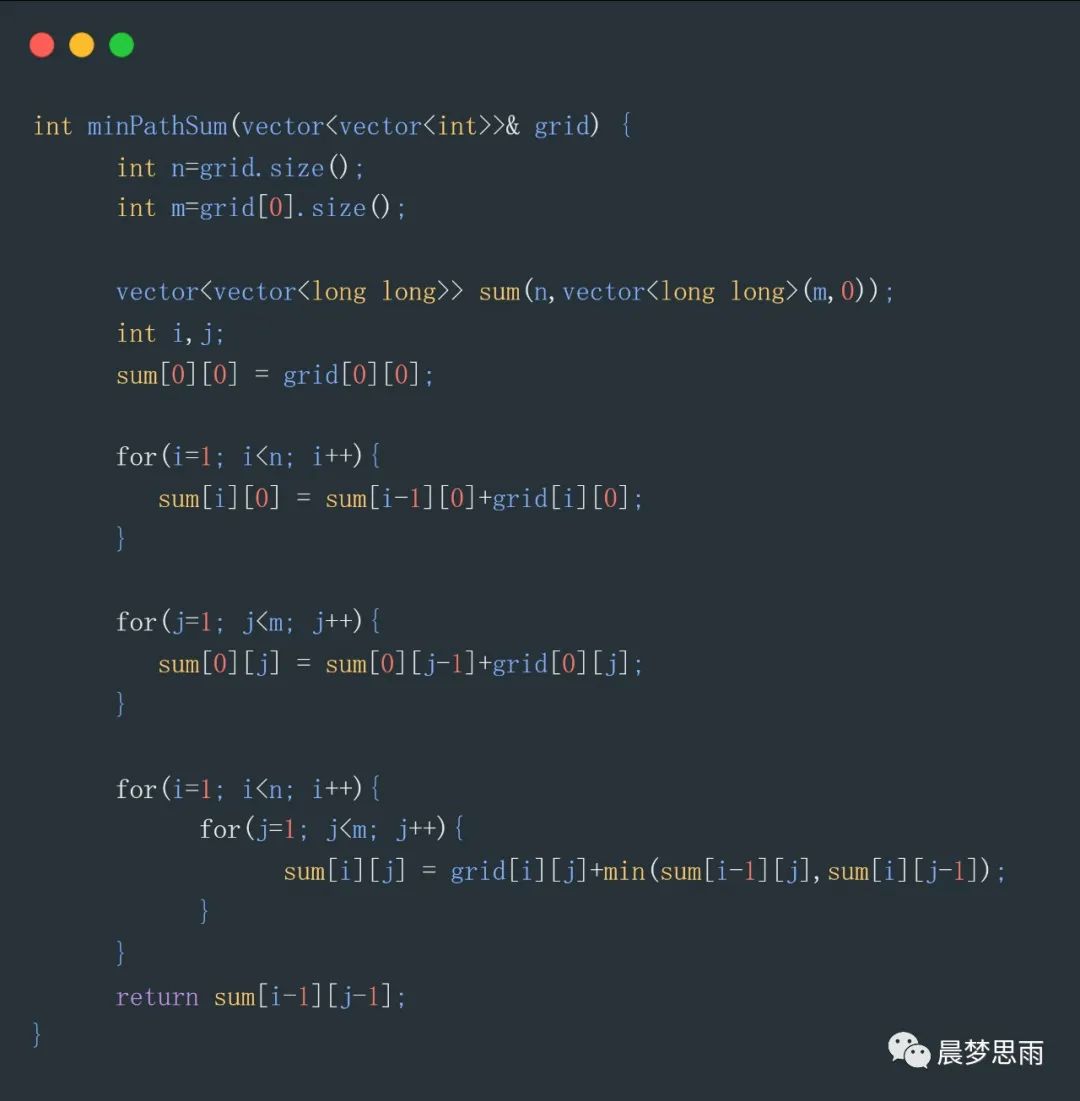
sum用來存儲,從[0][0]到sum[i][j]路徑的最小和,看看每次sum的變化,sum[1][1]=7意思是,從[0][0]到[1][1]路徑最小和是7。
程序先把,第2行對應的sum都求出來,再把第2列對應的sum都求出來,最后求sum[2][2]就很容易了。
最后,sum[i-1][j-1]就是推出的最小值,上述代碼就是dp方程的實現。
劃分數組為兩個相等的子集
題目:輸入:[1, 5, 11, 5], 輸出:[1, 5, 5]和[11]
思路是,相對數組中每個數求dp,最后就會找到dp[target]是否為true。
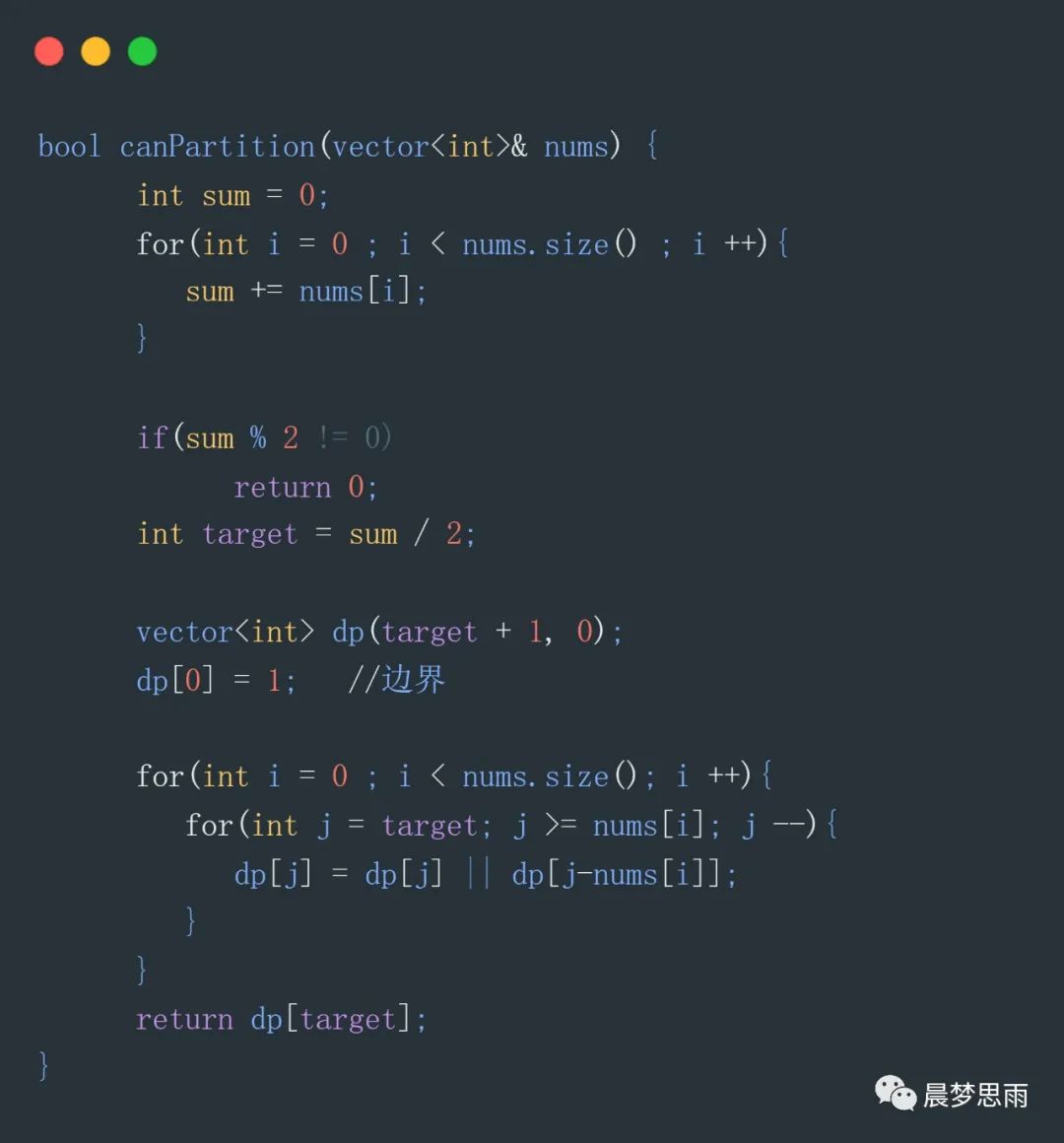
如果 dp[j - nums[i]] 為true的,說明可以組成 j-nums[i]這個數,再加上nums[i],就可以組成數字j。
當j = target是同樣道理,要想找到dp[target]為true,就找到數組中,幾個值的和為target時,對應下標的dp值為true,這樣反推dp[target]為true。
代碼如下:
乘積最大連續子數組
題目:
輸入一個整形數組,數組里有正數也有負數。數組中連續的一個,或多個整數組成一個子數組,每個子數組都有一個和。求所有子數組的和的最大值。
例如數組:arr[]={1, 2, 3, -2, 4, -3 } 最大子數組為 {1, 2, 3, -2, 4} 和為8。
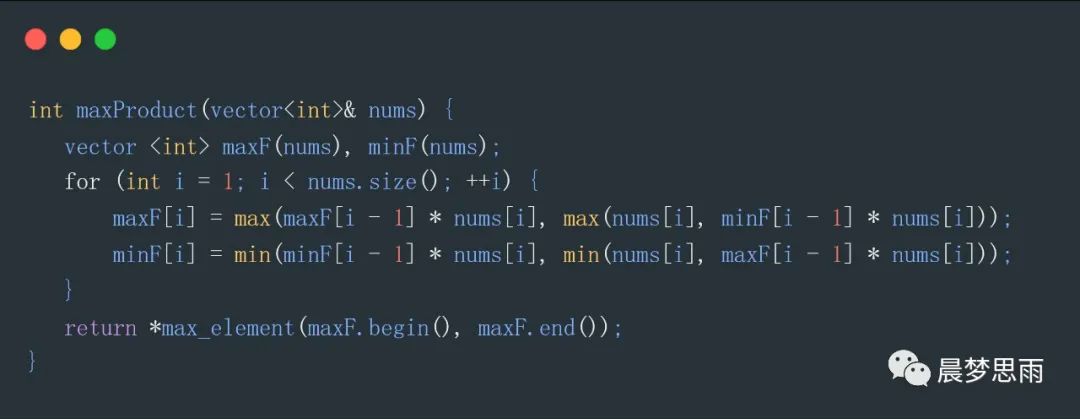
思路:fmax(i) 表示,以第 i 個元素結尾的,乘積最大子數組的乘積,fmin(i) 表示,以第 i 個元素結尾的,乘積最小子數組的乘積。
這里分為最大和最小是因為數組可能存在負數,最大值乘以負數變成較小值,最小值乘以一個負數也可能變成最大值。
比較方程是:當前數乘以上一個最大值,當前值,當前數乘以上一個最小值。這三者比較,其中的最大值,就是我們要的最大值。
同樣,每次也要把最小值計算出來,方式同上。
代碼如下:
等差遞減區間的個數
題目:求一個數組中等差遞減區間個數,等差數列必須是連續的。
例子:A = [1, 2, 3, 4],個數為3,分別是:[1, 2, 3], [2, 3, 4]
等差數列公式:
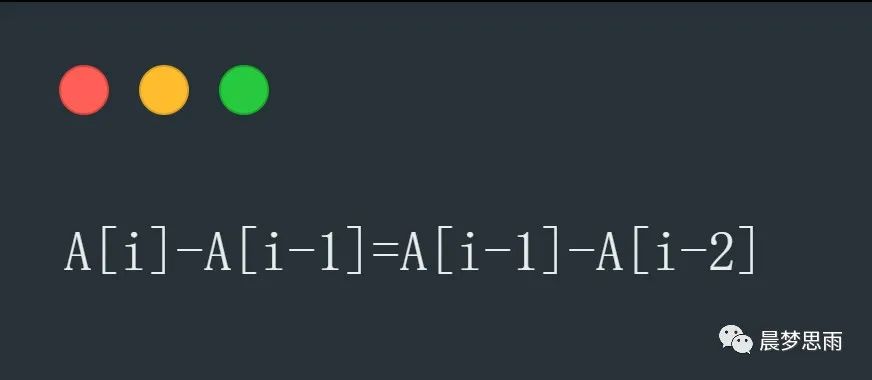
先看一個表:
| 數組 | 等差數列的數目 | 與上一組等差數列比較 |
| 1 23 | 1 | 1 - 0 = 1 |
| 12 3 4 | 3 | 3 - 1 = 2 |
| 12 3 45 | 6 | 6 - 3 = 3 |
| 1 2 3 4 5 6 | 10 | 10 - 6 =4 |
其實仔細觀察,發現這是一個斐波拉切數列,0,1….n-2數的求和,動態規劃找到方程了,就發現非常簡單了。
這就是規律,但需要自己去發現規律,有些題目咋看一臉懵逼,仔細看就會發現其中的規律。
dp[i] 表示到i位置時,子數組的個數。數組長度大于3。
下面看下代碼:
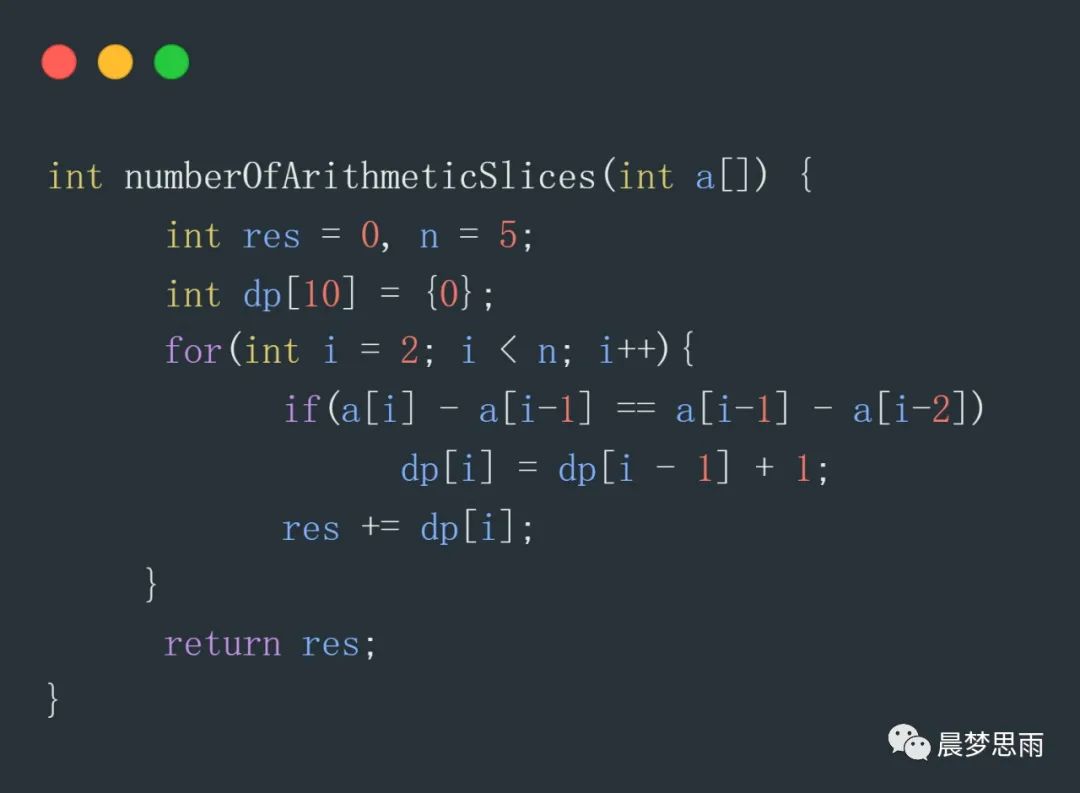
下面再看代碼執行值的變化過程:
| i值 | 子數組 | dp[i] | res |
| i = 2 | 123 | 1 | 1 |
| i = 3 | 123 2341234 | 2 | 3 |
| i = 4 | 123 2341234 2345 12345 | 3 | 6 |
| i = 5 | 123 2341234 2345 1234523456123456 | 4 | 10 |
很明顯,就是0,1….n-2數的求和。
最長回文子串
題目:求最長回文子串。輸入: "babad",輸出: "bab"。注意: "aba" 也是一個有效答案。
dp[i][j]表示,字符s從下標i到下標j,是否為回文串。
如果bab是回文串,那么ababa也是回文串。因為,在兩邊增加了相同的數。同理,可以給出動態方程:

下面看下代碼:
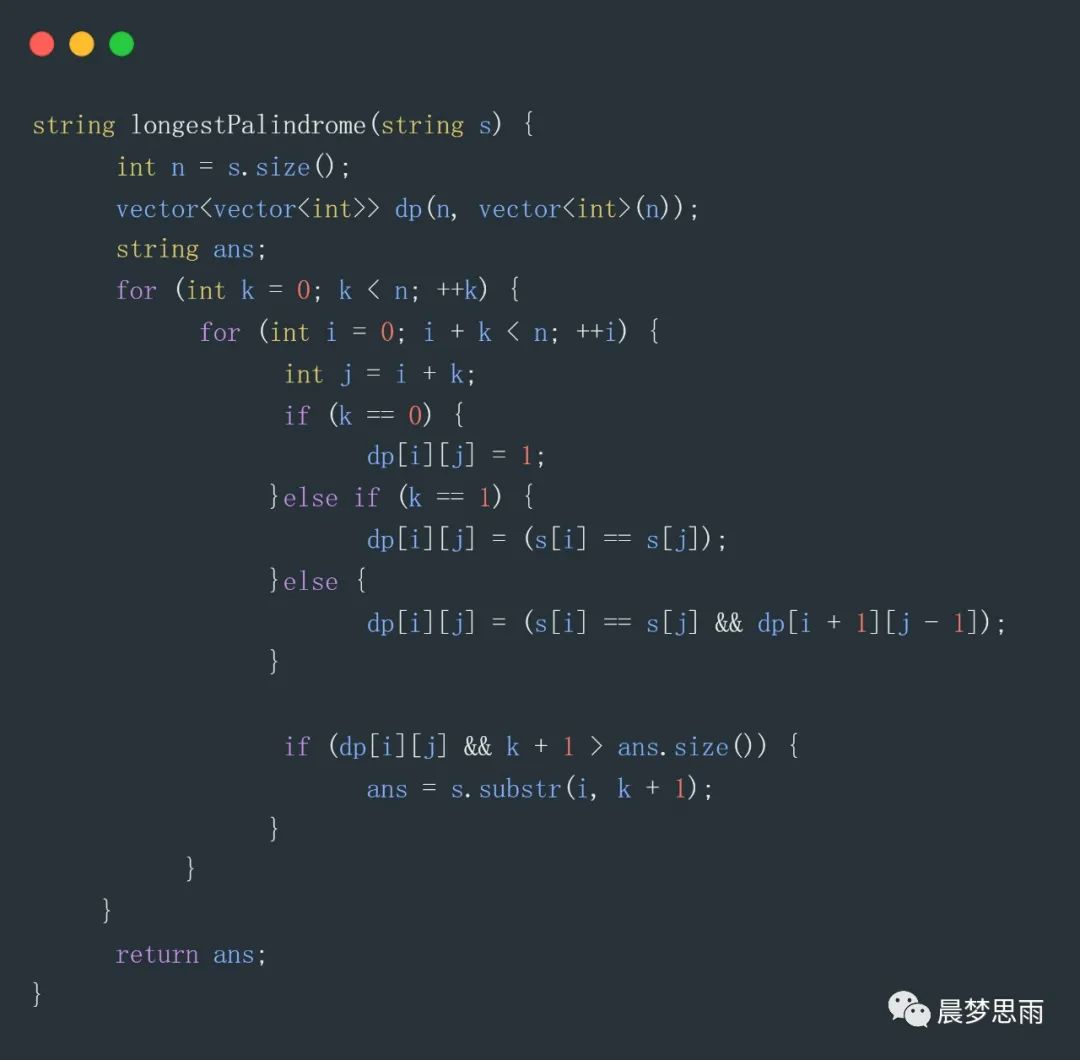
這段代碼用利用了dp[i + 1][j - 1],其前面已經計算出來了。
當k = 4時,字符串最長,最后符合條件的回文子串最長。注意整個循環遍歷的過程,用k最為兩個下標的間距,然后遍歷每種可能的結果,判斷是否回文。
最長的子串最后判斷,將符合條件的子串保存起來。動態規劃方程推測極為重要。
最長遞增子序列
求一個數組的最長自增子序列。
輸入: [10,9,2,5,3,7,101,18],輸出: 4。
解釋: 最長的上升子序列是 [2,3,7,101],它的長度是 4。
代碼如下:

dp[i]表示以a[i]這個元素結尾的最長遞增子序列的長度。
想求 dp[5] 的值,也就是想求以 nums[5] 為結尾,其最長遞增子序列。
nums[5] = 3,既然是遞增子序列。我們只要找到,前面那些結尾比 3 小的子序列,然后把 3 接到最后,就可以形成新的遞增子序列,而且這個新的子序列長度加一。
當然,可能形成很多種新的子序列,但是我們只要最長的,把最長子序列的長度作為 dp[5] 的值即可。
根據此依次類推到前面,d[0],d[1]…d[i]都是這樣求出來的,看來動態規劃有些是逆推的。
最大子序和
給定一個整數數組 nums ,找到一個具有最大和的連續子數組(子數組最少包含一個元素),返回其最大和。
輸入: [-2,1,-3,4,-1,2,1,-5,4],輸出: 6,解釋: 連續子數組 [4,-1,2,1] 的和最大,為 6
解決思路:動態規劃
動態規劃方程:

動態規劃:定義dp[i]表示為nums[i]為結尾的[連續子數組的最大和。
當遍歷到nums[i]時,我們需要比較nums[i]和dp[i-1]+nums[i]誰更大,然后取較大值。
代碼如下:

責任編輯:lq
-
算法
+關注
關注
23文章
4710瀏覽量
95378 -
動態規劃
+關注
關注
0文章
17瀏覽量
9018
原文標題:大廠動態規劃面試匯總,重量級干貨,徹夜整理
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
投入式水位計:助力水資源規劃與結構安全

AGV小車中的動態路徑規劃算法揭秘
AGV通信第2期 AGV集群智能路徑規劃解決方案

CADENAS 數字產品配置器輕松實現Ascendor電梯規劃
函數指針的六個常見應用場景

具身智能工業機器人路徑規劃算法成為破局關鍵
一些常見的動態電路
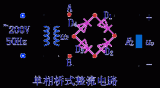
常見的動態電路圖

多臺倉儲AGV協作全局路徑規劃算法的研究






 常見的動態規劃題目
常見的動態規劃題目












評論