有時，我們需要測量低頻信號。例如，考慮在壓力變化非常緩慢的應用中使用的壓力傳感器。

我們測量的信號幾乎是直流電，但這會如何影響我們的設計？

我們知道在高頻下，事情會變得瘋狂，我們需要仔細注意設計的每一個細節。這可能會誤導我們錯誤地認為測量低頻信號是一項微不足道的工作。我們將看到情況并非一定如此。事實上，有一種稱為同步解調的技術，它有意增加工作頻率以實現更準確的測量。

低頻測量示例

在某些應用中，直接測量具有低頻輸出的傳感器（不應用同步解調）。例如，駐極體麥克風是一種特殊類型的可變電容，可以直接測量。駐極體麥克風的電容隨氣壓變化（聲波）而變化。

電容器結構中使用了一種稱為駐極體的 Teflon 類材料，其表面結合有固定電荷。由于電容器上的電荷是固定的，由氣壓變化引起的電容值的變化會導致電容器兩端的電壓發生相應的變化（對于電容器，我們有 Q=CV）。

如圖 1 所示，駐極體麥克風通常有一個內部 JFET，用作緩沖器。

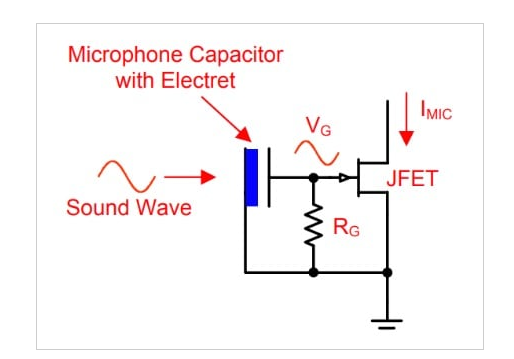
在此特定應用中，傳感器（麥克風）產生的信號直接應用于電路的放大元件。這種測量電容傳感器的方法有時被稱為“直接直流”方法，因為直接測量電容器上的低頻信號。

我們測量低頻信號時出現的主要問題之一是閃爍噪聲。

閃爍噪聲

閃爍噪聲的平均功率與工作頻率成反比（這就是閃爍噪聲也稱為 1/f 噪聲的原因）。因此，信號頻率越低，我們必須處理的噪聲功率就越大。圖 2 顯示了精密運算放大器ADA4622-2的電壓噪聲頻譜密度。

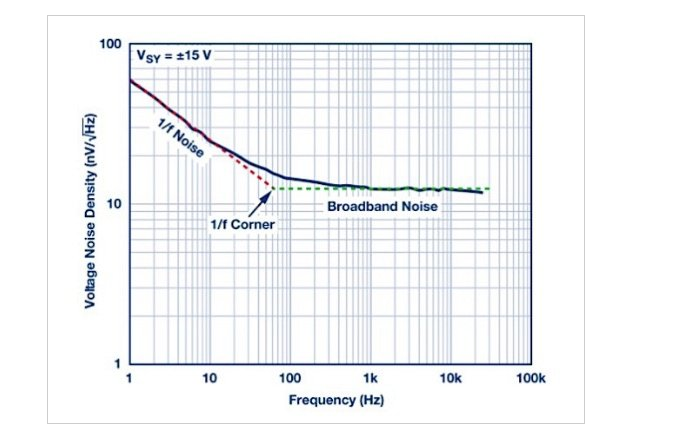
在大約 100 Hz 以上，噪聲功率幾乎均勻分布在不同頻率之間。噪聲曲線的該區域對應于器件的熱噪聲。然而，當我們移至低于 100 Hz 的頻率時，由于閃爍噪聲，噪聲平均功率會增加。

用直線近似噪聲分布的兩個不同區域，我們可以找到一個交點，稱為 1/f 噪聲角頻率（如圖 2 所示）。轉角頻率允許我們確定給定頻率下設備的主要噪聲類型（閃爍或熱）。

在 1/f 轉角頻率以下，傳感器產生的小信號可能完全被噪聲掩蓋。如果我們能以某種方式將傳感器輸出信號的頻率增加到轉角頻率以上，我們就可以進行更準確的測量。這是同步解調技術背后的基本思想。

圖 3 顯示了在更高頻率下進行測量如何將所需信號從設備閃爍噪聲中提取出來。

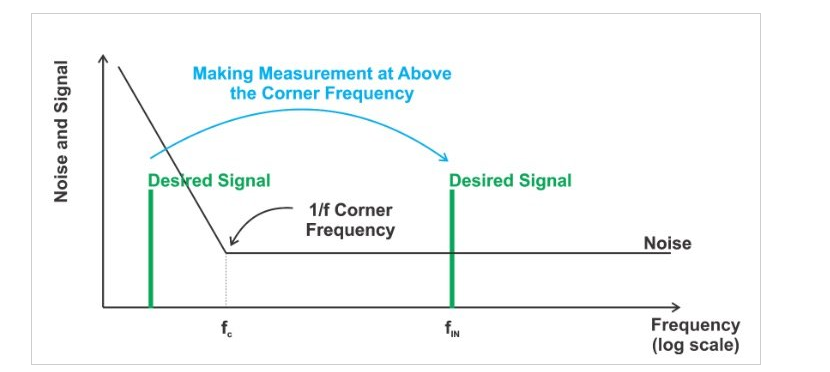
圖 3

對于圖 1 所示的“直接直流”測量，閃爍噪聲可能不是一個嚴重的問題，因為語音信號在非常低的頻率（低于約 20 Hz）下顯示的功率可以忽略不計。此外，我們或許能夠定制內部緩沖晶體管以降低其 1/f 轉角頻率。

然而，在某些應用中，傳感器的輸出信號頻率要低得多（幾乎是直流），我們需要更準確的測量。在這種情況下，電子元件的閃爍噪聲可以完全掩蓋傳感器產生的信號，我們需要同步解調等技術來規避閃爍噪聲問題。

傳感器的交流激勵

圖 4 說明了使用交流信號測量電容傳感器的情況。在該圖中，可變電容 C sense模擬了我們的電容傳感器。輸入電壓源施加頻率在 1 kHz-1 MHz 范圍內的正弦波。根據 C sense與 C 2的比率，電壓信號出現在運算放大器的輸入端。在這種情況下，可以選擇運算放大器的輸入信號，使其充分大于電路的 1/f 轉角頻率。這與“直接直流”方法形成對比，在這種方法中，測量信號可能處于非常低的頻率。

由于所需信號遠離 1/f 轉角頻率（如圖 5 所示），因此閃爍噪聲不是限制因素，我們可以檢測到小得多的信號。

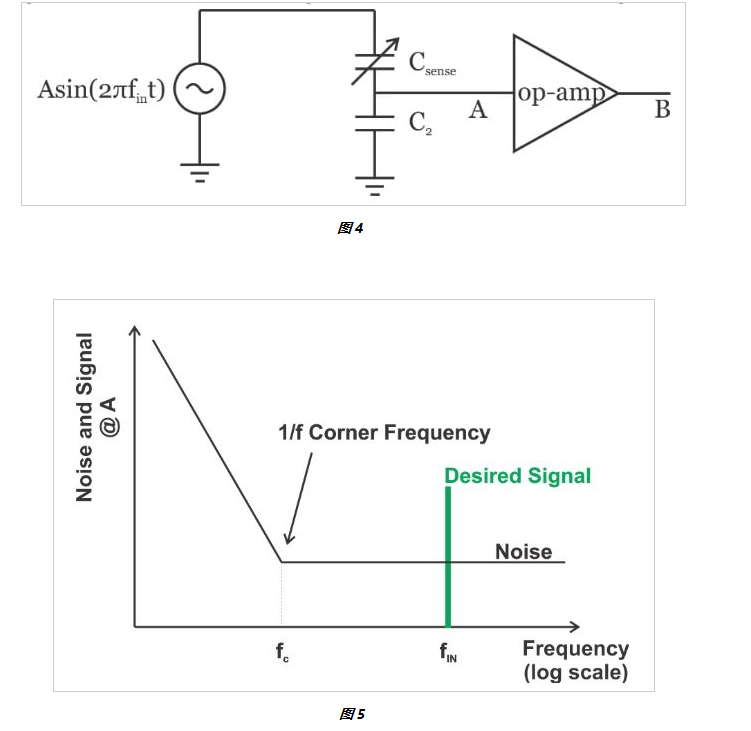
在運算放大器輸出端，我們有一個放大的信號，可用于確定可變電容的值；然而，我們需要一個帶通濾波器 （BPF） 來抑制噪聲成分并僅保留所需信號。這在圖 6 中進行了描述。

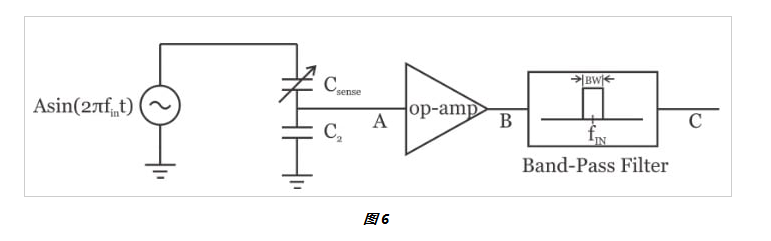
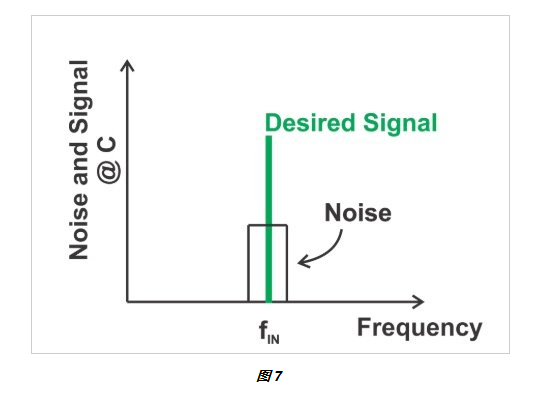
請注意，BPF 的中心頻率與輸入頻率相同。假設帶通濾波器是理想的，我們將獲得所需信號以及落在帶通濾波器通帶內的熱噪聲（下圖 7）。

使用 BPF 的限制

在圖 6 中，我們需要一個高 Q 帶通濾波器來充分抑制噪聲并保持所需信號。一個非常高 Q 值的濾波器可以讓我們拒絕大部分噪聲。但是，存在兩個主要問題：首先，實現高 Q 連續時間帶通濾波器可能具有挑戰性，尤其是在高頻下。事實上，隨著濾波器中心頻率的增加，實現給定的 Q 因子變得越來越困難。這是因為在高頻（大約幾百 MHz）下，運算放大器的放大能力有限，并且表現出非理想的相位響應。您可能會說圖 6 中濾波器的中心頻率在 1 kHz-1 MHz 范圍內，這并不是真正的高頻濾波器。嗯，你說得對，我們可以在這個頻率范圍內有一個高 Q 濾波器。然而，隨著頻率越來越高，我們必須消耗更多的能量。換句話說，對于給定的 Q 因子，我們期望較低頻率的濾波器表現出較低的功耗。因此，如果可以在較低的頻率下執行運算放大器之后的濾波，則功率效率會更高。

圖 6 所示概念的第二個問題是調諧帶通濾波器的中心頻率。請注意，模擬連續時間濾波器的中心頻率取決于電阻器、電容器和跨導體的值。這些參數的絕對值可能會有很大差異。因此，濾波器的中心頻率可能不完全在 f IN. 由于濾波器具有較窄的通帶，由于濾波器中心頻率的變化，所需信號很容易落在濾波器通帶之外。使用高 Q BPF 的第二個問題可能比上一段中討論的功率效率問題更具挑戰性。有趣的是，如果應用需要高 Q 連續時間帶通濾波器，我們必須采用一種機制來調諧濾波器中心頻率。例如，一些集成帶通濾波器應用使用一個在概念上類似于鎖相環的反饋環來調諧濾波器中心頻率。然而，這樣的系統對于讀取傳感器來說似乎過于復雜和耗電。在下一節中，我們將看到巧妙的調整可以使用低通濾波器而不是 BPF 來實現所需的濾波操作。通過這種方式，我們可以擁有一個不需要任何頻率調諧電路的低功耗解決方案。

同步解調

同步解調的概念如圖 8 所示。在該圖中，乘法器放置在運算放大器之后。

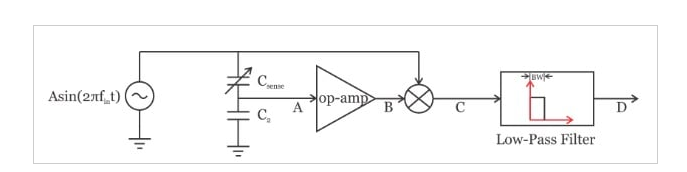
假設運放輸出的輸出信號為 v乙（噸）=乙秒一世n（2πF一世n噸+φ）v乙（噸）=乙秒一世n（2πF一世n噸+φ）。 該信號乘以輸入信號一種秒一世n（2πF一世n噸）一種秒一世n（2πF一世n噸） 這給出了：

vC（噸）=一種秒一世n（2πF一世n噸）×乙秒一世n（2πF一世n噸+φ）=12一種乙C○秒（φ）-12一種乙C○秒（4πF一世n噸+φ）vC（噸）=一種秒一世n（2πF一世n噸）×乙秒一世n（2πF一世n噸+φ）=12一種乙C○秒（φ）-12一種乙C○秒（4πF一世n噸+φ）

第一項是直流，但第二項是輸入頻率的兩倍。因此，窄低通濾波器可以去除第二項，我們有：

vD（噸）=12一種乙C○秒（φ）vD（噸）=12一種乙C○秒（φ）

如果我們假設運算放大器沒有引入任何延遲，即 φ=0φ=0， 我們獲得 vD（噸）=12一種乙vD（噸）=12一種乙。 如您所見，低通濾波器的輸出與節點 A 處的信號幅度成正比，可用于測量C秒電子n秒電子C秒電子n秒電子。 上述方法具有三個優點：

可以選擇傳感器輸出的頻率，使其充分高于 1/f 轉角頻率。

濾波器以盡可能低的頻率運行，并應消耗盡可能小的功率。

該濾波器不需要頻率調諧電路。

在本系列的下一篇文章中，我們將繼續討論并仔細研究同步解調技術的實現。

結論

“直接直流”方法直接測量電容傳感器產生的低頻信號。由于閃爍噪聲，這種低頻測量的精度可能會受到限制。為了規避這個問題，我們可以使用交流信號來激勵傳感器。由于測量發生在高于 1/f 轉角頻率的頻率上，因此閃爍噪聲不再是限制因素。在這種情況下，我們可以使用帶通濾波器來選擇所需的信號；然而，使用高 Q 帶通濾波器可能具有挑戰性。相反，我們可以同步解調被測信號并使用低通濾波器來執行所需的濾波。
責任編輯人：CC