模態(tài)分析主要研究頻率域內(nèi)系統(tǒng)動態(tài)特性。

通過模態(tài)分析方法搞清楚了結(jié)構(gòu)物在某一易受影響的頻率范圍內(nèi)的各階主要模態(tài)的特性，就可以預(yù)言結(jié)構(gòu)在此頻段內(nèi)在外部或內(nèi)部各種振源作用下產(chǎn)生的實(shí)際振動響應(yīng)。

模態(tài)分析主要分為解析模態(tài)分析和試驗(yàn)?zāi)B(tài)分析

解析模態(tài)分析

通常我們針對一個(gè)線性定常系統(tǒng)進(jìn)行動力學(xué)描述可以得到方程組：

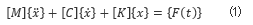
其中，[M] 是質(zhì)量矩陣，[C] 是阻尼矩陣，[K] 是剛度矩陣，{x(t)} 是位移向量, {F(t)} 是力矩陣。 我們的目標(biāo)是求解這個(gè)線性定常系統(tǒng)振動微分方程組得到 {x(t)}，也就是系統(tǒng)上各點(diǎn)隨時(shí)間的位移。 對于單自由度的系統(tǒng)是方便求解的，所以對于這種多自由度系統(tǒng)我們首先想到的是通過坐標(biāo)變換，用一組新的正交基（模態(tài)空間里的基）去描述 {x(t)}，例如 [P?1]x(t)，來實(shí)現(xiàn)對方程組 (1) 解耦，從而將問題轉(zhuǎn)化為互相獨(dú)立的子方程（組），用更少自由度甚至單自由度的方程進(jìn)行求解。 其中[P?1]就是模態(tài)矩陣，其每列為模態(tài)振型，它描述的是在新的解耦后的坐標(biāo)系中的各維坐標(biāo)與原來坐標(biāo)系中各個(gè)維度的線性關(guān)系。

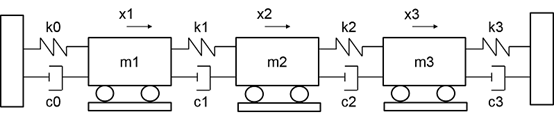
例如對于一個(gè)簡化的多自由度的彈簧系統(tǒng)，這個(gè)線性定常系統(tǒng)由 3 個(gè)相同重量的模塊組成，m?=m?=m?=m，他們中間用彈簧鏈接, 為了簡化問題，我們設(shè)彈簧的勁度系數(shù) k?=k?=k?=k?=k，阻尼系數(shù) c?=c?=c?=c?=0。 定義 x?,x?,x??為每個(gè)質(zhì)量塊的位移，另外 k? ,k?邊緣兩端的位移。由于兩端固定，都為0。每個(gè)質(zhì)量塊的運(yùn)動方程分別為：

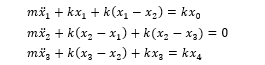
將上述方程寫為矩陣形式，上述運(yùn)動學(xué)方程組可以簡化為：

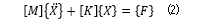
其中

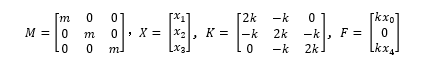
對于方程組 (2)，如何進(jìn)行坐標(biāo)解耦呢？ 計(jì)算時(shí)運(yùn)動學(xué)方程組(2) 右側(cè)項(xiàng)可以忽略, 只保留質(zhì)量矩陣項(xiàng) [M] 和剛度矩陣 [K] 項(xiàng)，即

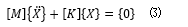
對于方程組(3) 通常的做法是轉(zhuǎn)換為：

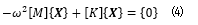
本質(zhì)對方程組(4) 解耦實(shí)際上就是求解質(zhì)量矩陣關(guān)于剛度矩陣的廣義特征值的問題。也就是計(jì)算得到特征值，

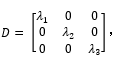
和特征向量，

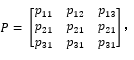
使得[M][P]=[K][P][D] (5) 其中特征向量 [P] 即為模態(tài)向量（空間基向量），為對應(yīng)的特征值對角陣對應(yīng)解耦后固有頻率的平方，即

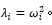
具體此處不做推導(dǎo)，但可以簡單的從必要性上進(jìn)行解釋： 假設(shè)已經(jīng)通過空間變換矩陣得到新的坐標(biāo)

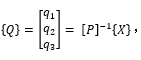
我們計(jì)算一下特征向量矩陣是否將原始方程組坐標(biāo)由 {X} 變換為后 {Q} 得到單自由度的二階常微分方程組。 我們將{X}=[P]{Q} 帶入方程(3)得到

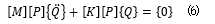
同時(shí)我們將(5) 帶入(6) 可以得到

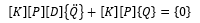
在 [K][P] 均可逆的條件下，我們得到方程

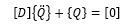
即：

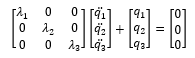
也就是完全解耦的單自由度的二階常微分方程，接下來可以單獨(dú)求解 q?(t), q?(t), q?(t), 最后只需要再做一次 [P] 變換將模態(tài)空間坐標(biāo)變換到物理坐標(biāo)即可。

?????????

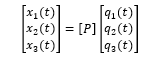
% 'M' 是質(zhì)量矩陣,'K' 是剛度矩陣. 'm' 質(zhì)量塊質(zhì)量,單位 Kgs

% 'k' 剛度系數(shù),單位N/m. 'P' 和'D' 是特征向量和特征值.

m = 0.003;

k = 180000;

M = m*eye(3);

K = k*[2 -1 0 ;

-1 2 -1 ;

0 -1 2 ];

% P為特征向量：變換矩陣，D為特征值：固有頻率的平方，w_nat 包含自然響應(yīng)頻率.

[P,D] = eig(K,M)

w_nat = sqrt(D)

% 我們查看低階模態(tài)振型，也就是低頻振型，可以嘗試設(shè)置number

% 查看三階模態(tài)振型'EIGS' 函數(shù)可以用來計(jì)算特征值和特征向量

number = 3;

[P,D]=eigs(K,M,number,'smallestabs');

% 因?yàn)橄到y(tǒng)兩端固定，模態(tài)振型坐標(biāo)在這兩端為0

vect_aug1 = [0 0 0;P;0 0 0];

c = ['m','b','r'];

figure(1)

for i=1:size(vect_aug1,2)

plot(vect_aug1(:,i),c(i))

hold on;

end

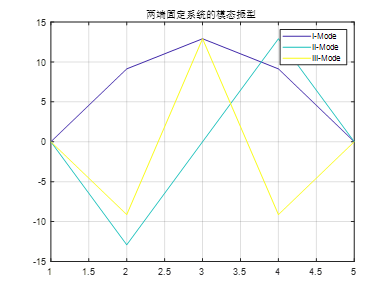
最終

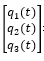
和

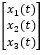
的求解以及繪制都可以用通過 MATLAB 腳本實(shí)現(xiàn)。大家可以自己嘗試。 當(dāng)然對于我們的系統(tǒng)不可能是這種簡單的系統(tǒng)，通常要結(jié)合有限元的手段進(jìn)行計(jì)算。 MATLAB 中的 Partial Differential EquationToolbox 對于滿足我們一些基礎(chǔ)的需求可以提供求解方案。 我們看一個(gè)基于 MATLAB 有限元計(jì)算模態(tài)的示例。 本示例是對 KinovaGen3 機(jī)械臂肩部關(guān)節(jié)部件進(jìn)行模態(tài)和頻率響應(yīng)分析。機(jī)械臂通過多個(gè)關(guān)節(jié)鏈接，一端固定。這些鏈接結(jié)構(gòu)強(qiáng)度要夠大以避免電機(jī)帶動負(fù)載運(yùn)動時(shí)產(chǎn)生振動。 機(jī)械臂終端的負(fù)載會讓每個(gè)鏈接處產(chǎn)生壓力。壓力的方向取決于負(fù)載的方向。此示例主要展示如何分析 Kinova Gen3 超輕量級機(jī)械臂的肩部關(guān)節(jié)連接部件在一定壓力下可能的形變。

模態(tài)分析MATLAB 中有限元求解流程

model = createpde('structural','modal-solid');

importGeometry(model,'Gen3Shoulder.stl');

generateMesh(model);

structuralProperties(model,'YoungsModulus',E, ...

'PoissonsRatio',nu, ...

'MassDensity',rho);

將 facelabel 可視化出來方便設(shè)置邊界約束和負(fù)載。

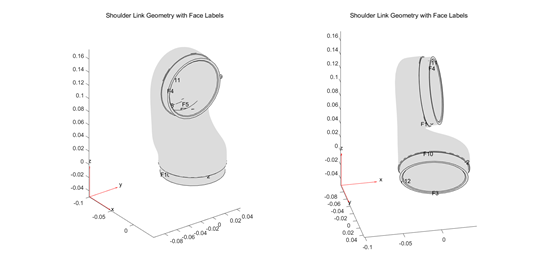
face3 是固定的，face4 是活動的。設(shè)置約束

structuralBC(model,'Face',3,'Constraint','fixed');

在關(guān)心的頻率范圍進(jìn)行模型求解。

RF = solve(model,'FrequencyRange',[-1,10000]*2*pi);

modeID = 1:numel(RF.NaturalFrequencies);

通過對結(jié)果除以2pi,得到Hz單位的頻率值：

tmodalResults = table(modeID.',RF.NaturalFrequencies/2/pi);

tmodalResults.Properties.VariableNames = {'Mode','Frequency'};

disp(tmodalResults);

同樣我們需要可視化模態(tài)振型。最好的方式是以各階模態(tài)頻率的簡諧振動動畫顯示出來，此處顯示前六階模態(tài)振型：

頻率響應(yīng)分析模擬機(jī)械臂關(guān)節(jié)在壓力載荷下的動力學(xué)，假設(shè)附加其上的連桿對各半面分別施加大小相等方向相反的壓力。分析面上某點(diǎn)的頻率響應(yīng)和形變。

同樣跟上述流程一樣，創(chuàng)建結(jié)構(gòu)，導(dǎo)入幾何形狀，生成網(wǎng)格。

其他過程跟模態(tài)分析相同，區(qū)別在于加一個(gè)力，使用 pressFcnFR 函數(shù)在面 4 上施加邊界載荷。 這個(gè)函數(shù)作用一個(gè)推力和一個(gè)扭轉(zhuǎn)壓力信號。推壓分量是均勻的。扭力對左側(cè)面施加正壓力，對右側(cè)施加負(fù)壓力。

structuralBoundaryLoad(fmodel,'Face',4,'Pressure',@(region,state)pressFcnFR(region, state),'Vectorized','on');

這個(gè)壓力函數(shù)跟頻率無關(guān)，作用于所有頻率。

同樣進(jìn)行求解

R = solve(fmodel,flist,'ModalResults',RF)

我們可以看面 4對應(yīng)的負(fù)向負(fù)荷最大的點(diǎn)（0.003; 0.0436; 0.1307）對應(yīng)的位移

queryPoint= [0.003; 0.0436; 0.1307];

queryPointDisp =R.interpolateDisplacement(queryPoint);

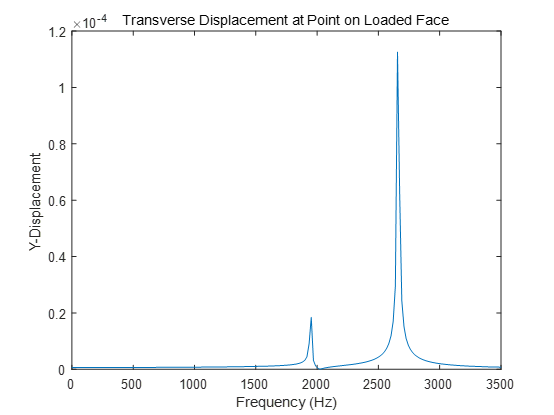
響應(yīng)的峰值出現(xiàn)在 2662Hz 附近，與二階模態(tài)接近。在接近 1947Hz 的一階模態(tài)上也會出現(xiàn)小的響應(yīng)。

通過使用 max 函數(shù)找到峰值響應(yīng)頻率對應(yīng)的峰值和索引。

[M, I] = max(abs(queryPointDisp.uy))

M = 1.1256e-04

I = 152 繪制峰值響應(yīng)頻率處的變形。

可以看到所施加的載荷主要激發(fā)了部件的開口模態(tài)和彎曲模態(tài)。 通過上面兩個(gè)示例，我們針對計(jì)算模態(tài)的場景可以在 MATLAB 中通過相應(yīng)的內(nèi)置函數(shù)做探索研究。

試驗(yàn)?zāi)B(tài)分析

試驗(yàn)?zāi)B(tài)分析主要是通過實(shí)測實(shí)驗(yàn)數(shù)據(jù)進(jìn)行頻率響應(yīng)估計(jì)并計(jì)算相應(yīng)模態(tài)參數(shù)的一種方法。

我們通過 MATLAB 自帶的一個(gè)例子來介紹試驗(yàn)?zāi)B(tài)分析。

詳見：https://ww2.mathworks.cn/help/releases/R2021a/ident/ug/modal-analysis-of-a-flexible-flying-wing-aircraft.html

這是明尼蘇達(dá)大學(xué)無人飛行器實(shí)驗(yàn)室的小型柔性飛翼飛機(jī)的示例。這個(gè)例子展示了柔性機(jī)翼飛機(jī)彎曲模態(tài)的計(jì)算過程。

通過沿翼型進(jìn)行機(jī)翼的振動響應(yīng)的多點(diǎn)采集獲得數(shù)據(jù)，用于辨識系統(tǒng)的動態(tài)模型。

從辨識出的模型中提取模態(tài)參數(shù)。

將模態(tài)參數(shù)數(shù)據(jù)與傳感器位置信息相結(jié)合，可視化機(jī)翼的各種彎曲模態(tài)。

實(shí)驗(yàn)設(shè)置

實(shí)驗(yàn)的目的是收集飛機(jī)在外部激勵下不同位置的振動響應(yīng)。

這架飛機(jī)懸掛在一個(gè)木制框架上，其重心由一根彈簧支撐。該彈簧具有足夠的彈性保證彈簧-質(zhì)量振蕩的固有頻率不會干擾飛機(jī)的基頻。通過一個(gè)電動激振器在飛機(jī)中心附近施加輸入力。

沿著翼展放置 20 個(gè)加速度計(jì)來收集振動響應(yīng)，如下圖所示

激振器輸入命令指定為一個(gè)恒定振幅的 chirp 信號 Asin(ω(t)t), chirp 信號的頻率隨時(shí)間線性增加，ω(t)=c0+c1t, 頻率范圍為 3 - 35hz。試驗(yàn)數(shù)據(jù)由兩個(gè)加速度計(jì)(在 x 方向的前緣和后緣)一次收集。總共進(jìn)行了 10 組實(shí)驗(yàn)來收集所有 20 個(gè)加速度計(jì)的響應(yīng)。加速度計(jì)和力傳感器的測量頻率都是 2000hz。

數(shù)據(jù)準(zhǔn)備

數(shù)據(jù)由 10 組單輸入/雙輸出信號表示，每組包含 600K 個(gè)樣本。

變量 MeasuredData 是一個(gè)結(jié)構(gòu)體。結(jié)構(gòu)體的每個(gè)域還是一個(gè)結(jié)構(gòu)體，包含兩個(gè)響應(yīng) y 和對應(yīng)輸入 u。隨機(jī)繪制第一次實(shí)驗(yàn)的數(shù)據(jù)。

fs = 2000; % data sampling frequency

Ts = 1/fs; % sample time

y = MeasuredData.Exp1.y; % 加速度計(jì)的輸出值，每個(gè)包含兩列

u = MeasuredData.Exp1.u; % input force data

t = (0:length(u)-1)' * Ts;

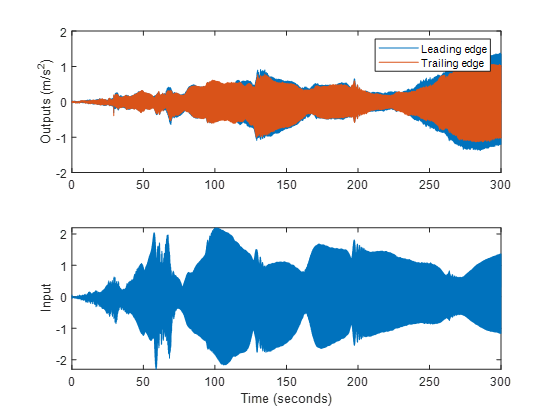
為了用于系統(tǒng)辨識，將數(shù)據(jù)封裝到 iddata 對象中，并將 10 次試驗(yàn)合并。

Data = merge(Data{:})

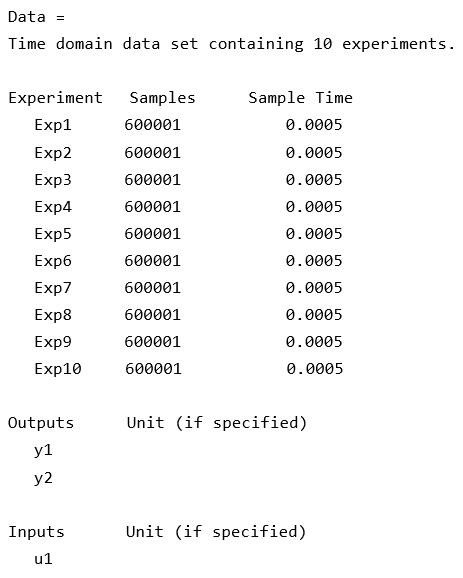
系統(tǒng)辨識

我們想識別一個(gè)頻率響應(yīng)與實(shí)際飛機(jī)盡可能接近的動態(tài)模型。

動態(tài)模型將系統(tǒng)的輸入和輸出之間的數(shù)學(xué)關(guān)系轉(zhuǎn)化為微分方程或差分方程。例如傳遞函數(shù)和狀態(tài)空間模型都是動態(tài)模型。

動態(tài)模型可以通過在時(shí)域或頻域?qū)υ囼?yàn)測量數(shù)據(jù)運(yùn)行 fest 和 sest 之類的模型估計(jì)命令來創(chuàng)建。

這個(gè)例子中，我們先用 etfe 命令進(jìn)行傳遞函數(shù)估計(jì)，從而將測量數(shù)據(jù)從時(shí)域轉(zhuǎn)換為頻率響應(yīng)。然后利用估計(jì)的頻響函數(shù)用于辨識飛機(jī)振動響應(yīng)的狀態(tài)空間模型。

當(dāng)然直接利用時(shí)域數(shù)據(jù)進(jìn)行狀態(tài)空間模型辨識也是可以的。但頻響函數(shù)的形式可以將大數(shù)據(jù)集壓縮成更少的樣本，并且更方便的在相關(guān)的頻率范圍調(diào)整估計(jì)過程。

針對每組實(shí)驗(yàn)數(shù)據(jù)（兩輸出/單輸入）進(jìn)行頻響函數(shù)(FRF)估算。使用 24000 個(gè)頻率點(diǎn)進(jìn)行無窗響應(yīng)計(jì)算。

G = cell(1, 10);

N = 24000;

for k = 1:10

% Convert time-domain data into a FRF using ETFE command

Data_k = getexp(Data, k);

G{k} = etfe(Data_k, [], N); % G{k} is an @idfrd object

end

G = cat(1,G{:}); % 將所有的頻響函數(shù)合并為一個(gè)（20輸出/一個(gè)輸入）的頻響

G.OutputName = 'y'; % name outputs 'y1', 'y2', ..., 'y20'

G.InterSample = 'bl';

我們隨便挑選第 1 個(gè)和第 15 個(gè)輸出幅值進(jìn)行繪制來看一下頻率響應(yīng)函數(shù)的估計(jì)結(jié)果。我們關(guān)注的頻率范圍(4 - 35hz)。

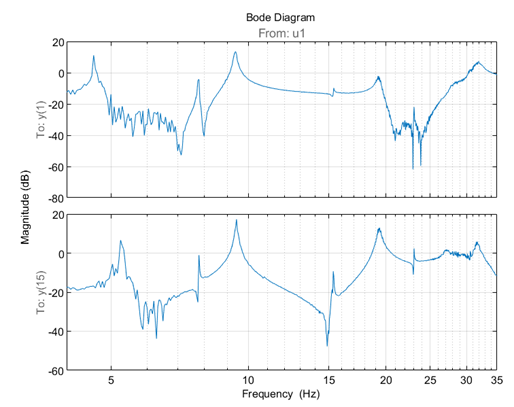
頻響函數(shù)顯示至少 9 個(gè)諧振頻率(峰值)。我們最關(guān)心飛機(jī)的機(jī)翼彎曲模態(tài)，這些模態(tài)主要集中在 6- 35hz 的頻率范圍，因此我們只選擇這個(gè)范圍的頻響。

f =G.Frequency/2/pi; % 單位變換

Gs = fselect(G,f>6 & f<=32)??? % 選擇頻響頻率范圍 (6.5 - 35 Hz)

接下來，計(jì)算一個(gè)狀態(tài)空間模型來逼近 Gs。子空間估計(jì)器 n4sid 提供了一個(gè)快速的非迭代估計(jì)。狀態(tài)空間模型參數(shù)配置會影響精度:

1. 模型階數(shù)的選擇。通常要多次嘗試。

2. 模型結(jié)構(gòu)。例如是否包含饋通項(xiàng)(狀態(tài)空間模型中的 D 矩陣是否為零)，等等。

3. 設(shè)置權(quán)重項(xiàng)，確保低振幅和高振幅對結(jié)果有相同的影響。

FRF =squeeze(Gs.ResponseData);

Weighting = mean(1./sqrt(abs(FRF))).';

n4Opt =n4sidOptions('EstimateCovariance',false,...

'WeightingFilter',Weighting,...

'OutputWeight',eye(20));

sys1 = n4sid(Gs,24,'Ts',0,'Feedthrough',true,n4Opt);

Fit = sys1.Report.Fit.FitPercent'

通過查看 Fit 的效果，顯示這 20 個(gè)響應(yīng)中最好的和最差的

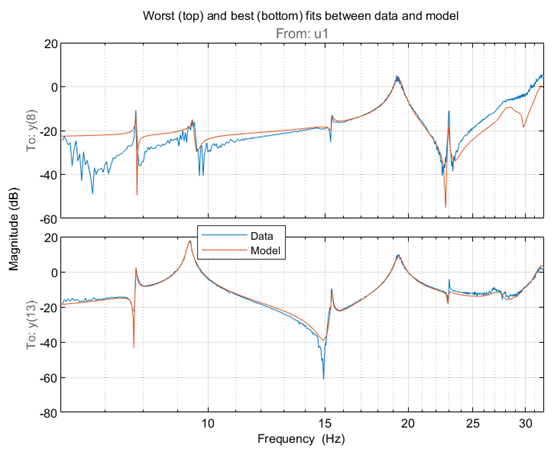
可以看到 sys1 結(jié)果仍然有待提高。通過對模型參數(shù)進(jìn)行非線性最小二乘優(yōu)化迭代，可以進(jìn)一步改善模型的擬合效果。這可以使用 sest 命令來實(shí)現(xiàn)。這一次也估計(jì)了參數(shù)協(xié)方差。

ssOpt = ssestOptions('EstimateCovariance',true,...

'WeightingFilter',n4Opt.WeightingFilter,...

'SearchMethod','lm',... % use Levenberg-Marquardt search method

'Display','on',...

'OutputWeight',eye(20));

sys2 = ssest(Gs, sys1, ssOpt); % estimate state-space model (this takesseveral minutes)

Fit = sys2.Report.Fit.FitPercent'

我們同樣看看擬合效果：最好的和最差的幅值進(jìn)行可視化。同時(shí)將 1-sd 置信區(qū)間可視化出來。

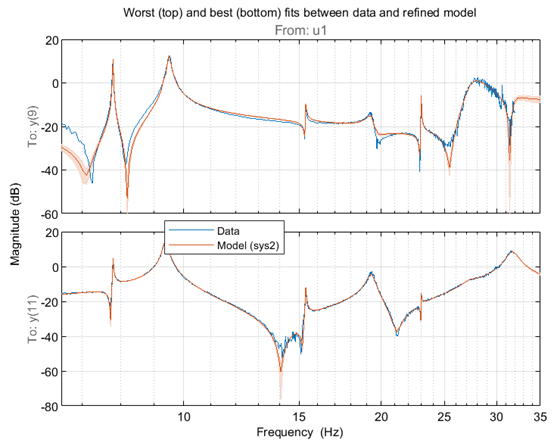
優(yōu)化后的狀態(tài)空間模型 sys2 在 7 - 20hz 區(qū)域的頻響擬合效果很好。多數(shù)共振位置的不確定性區(qū)間都很窄。我們最開始設(shè)置的是一個(gè) 24 階模型，這意味著在系統(tǒng) sys2 中最多有 12 個(gè)諧振模態(tài)。使用 modalfit 命令獲取這些模態(tài)的固有頻率。

f = Gs.Frequency/2/pi; % data frequencies (Hz)

fn = modalfit(sys2, f, 12); % naturalfrequencies (Hz)

fn 中的值表明兩個(gè)頻率非常接近 7.8 Hz，三個(gè)接近 9.4 Hz。查看這些頻率附近的各點(diǎn)頻率響應(yīng)，峰值位置在輸出中確實(shí)發(fā)生了一些偏移。

這些差異可以通過更好地控制實(shí)驗(yàn)過程，直接利用頻率為中心的狹窄范圍內(nèi)的時(shí)域數(shù)據(jù)進(jìn)行直接辨識，或?qū)⑦@些頻率附近的頻率響應(yīng)擬合為單個(gè)振動模態(tài)。本例中不討論這些替代方案。

模態(tài)參數(shù)計(jì)算

現(xiàn)在我們可以使用模型 sys2 來提取模態(tài)參數(shù)。通過查看頻響結(jié)果找到 10 個(gè)模態(tài)頻率，大約在頻率 [5 7 10 15 17 23 27 30]Hz 附近左右。通過使用 modalsd 函數(shù)可讓估計(jì)更加準(zhǔn)確，該函數(shù)嘗試不同模型的階數(shù)來檢查模態(tài)參數(shù)的穩(wěn)定性。

通過穩(wěn)定圖可以看到一組更好的自然響應(yīng)頻率

Freq = [7.8 9.4 15.3 19.3 23.0 27.3 29.231.7];

我們使用 Freq 向量的值作為從模型 sys2 中選擇主要模態(tài)的基準(zhǔn)。使用 modalfit 函數(shù)實(shí)現(xiàn)

[fn,dr,ms] = modalfit(sys2,f,length(Freq),'PhysFreq',Freq);

fn 是固有頻率 (Hz)， dr 是相應(yīng)的阻尼系數(shù)，ms 是模態(tài)振型向量 (每個(gè)固有頻率一列)。

模態(tài)振型可視化

我們使用上述模態(tài)參數(shù)可視化各種彎曲模態(tài)。此外，我們需要各測量點(diǎn)位置的信息。

模態(tài)振型包含在矩陣 ms 中，其中每一列對應(yīng)于一個(gè)頻率的振型。通過在加速度傳感器位置坐標(biāo)上疊加模態(tài)振型的振幅并以模態(tài)固有頻率改變振幅來做動畫展示。

結(jié)論

這個(gè)例子展示了一種基于參數(shù)模型辨識的模態(tài)參數(shù)估計(jì)方法。利用 24 階狀態(tài)空間模型，在 6 ~ 32 Hz 頻率范圍內(nèi)提取了 8 個(gè)穩(wěn)定的振動模態(tài)。將模態(tài)信息與位置信息相結(jié)合，可視化各種彎曲模態(tài)。

當(dāng)然，您也可以對其他設(shè)備例如風(fēng)力發(fā)電機(jī)的葉片振型進(jìn)行計(jì)算，了解風(fēng)力機(jī)葉片的動態(tài)特性從而優(yōu)化運(yùn)行效率和預(yù)測葉片失效，可以按同樣的思路實(shí)現(xiàn)。