三維點(diǎn)云數(shù)據(jù)用于表征目標(biāo)表面的海量點(diǎn)集合,但是各個(gè)離散點(diǎn)之間并沒(méi)有拓?fù)潢P(guān)系,一般通過(guò)建立點(diǎn)云的空間索引來(lái)實(shí)現(xiàn)基于鄰域關(guān)系的快速查找。在三維點(diǎn)云數(shù)據(jù)中用的較為廣泛的兩種結(jié)構(gòu)分別是Kdtree和Octree。
目錄
什么是Kdtree
什么是Octree
對(duì)比總結(jié)
什么是Kdtree?
1. Kdtree的原理
Kdtree是一種劃分k維數(shù)據(jù)空間的數(shù)據(jù)結(jié)構(gòu),在一個(gè)K維數(shù)據(jù)集合上構(gòu)建一棵Kdtree代表了對(duì)該K維數(shù)據(jù)集合構(gòu)成的K維空間的一個(gè)劃分,即樹(shù)中的每個(gè)結(jié)點(diǎn)就對(duì)應(yīng)了一個(gè)K維的超矩形區(qū)域。主要用于多維空間關(guān)鍵數(shù)據(jù)的搜索。
2. Kdtree的創(chuàng)建
Kdtree的創(chuàng)建就是按照某種順序?qū)o(wú)序化的點(diǎn)云進(jìn)行有序化排列,方便進(jìn)行快捷高效的檢索。算法流程如下:
(1) 在K維數(shù)據(jù)集合中選擇具有最大方差的維度,然后在該維度上選擇中值m為中心對(duì)該數(shù)據(jù)集合進(jìn)行劃分,得到兩個(gè)子集合;同時(shí)創(chuàng)建一個(gè)樹(shù)結(jié)點(diǎn)node,用于存儲(chǔ);
(2)對(duì)兩個(gè)子集合重復(fù)(1)步驟的過(guò)程,直至所有子集合都不能再劃分為止;如果某個(gè)子集合不能再劃分時(shí),則將該子集合中的數(shù)據(jù)保存到葉子結(jié)點(diǎn)。
根據(jù)上述算法步驟,以二維數(shù)據(jù)創(chuàng)建Kdtree為例,輸入數(shù)據(jù)列表為{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)};劃分的二維分割圖如下:
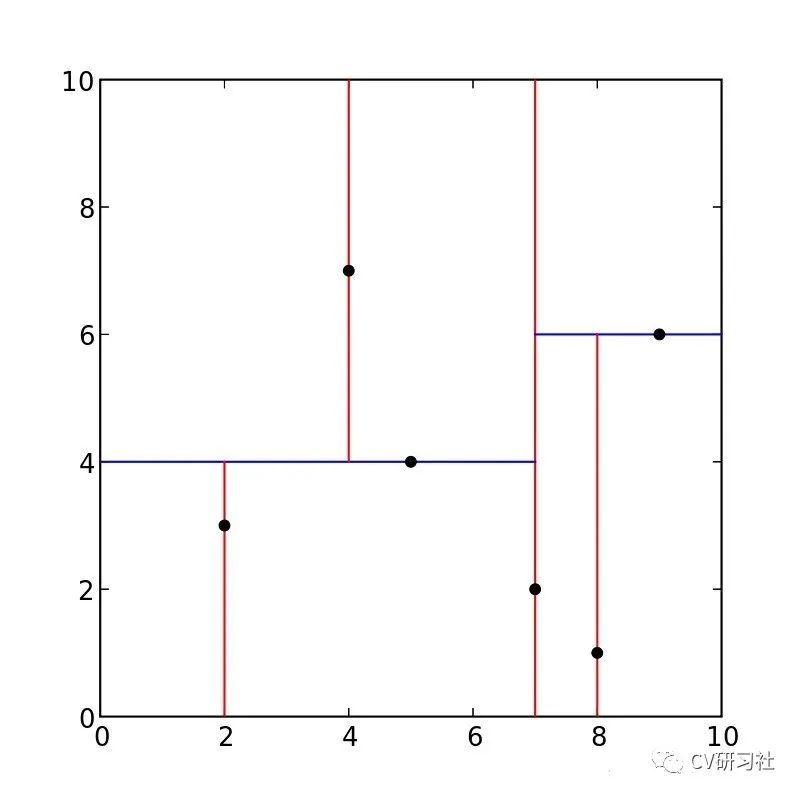
首先統(tǒng)計(jì)X和Y方向上的方差,選取方差較大的X維度作為初始分割軸,對(duì)X軸上的數(shù)值{2,5,9,4,8,7}取中值X=7作為分割線,生成左子樹(shù){(2,3),(5,4),(4,7)},生成右子樹(shù){(9,6),(8,1)},更新分割軸Y,分別在左右子樹(shù)中找到中位數(shù)(5,4)和(9,6),依次迭代如下圖:
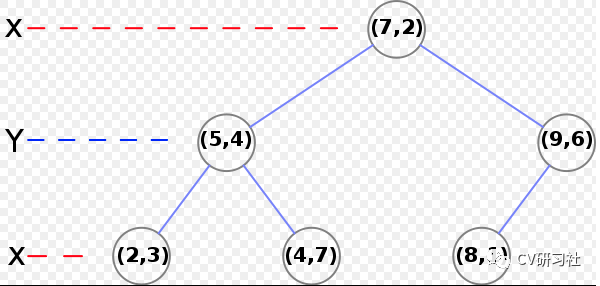
3. Kdtree的搜索
Kdtree的搜索方法有以下兩種:
范圍搜索:給定搜索點(diǎn)和搜索距離的閾值,從數(shù)據(jù)集中找出所有與搜索點(diǎn)距離小于閾值的數(shù)據(jù);
最近鄰搜索:給定查詢點(diǎn)和正整數(shù)K,從數(shù)據(jù)集中找到距離查詢點(diǎn)最近的K個(gè)數(shù)據(jù),當(dāng)K=1時(shí),就是最近鄰搜索。
以最近鄰搜索算法為例,其流程如下:
(1)將查詢數(shù)據(jù)Q從根結(jié)點(diǎn)開(kāi)始,按照Q與各個(gè)結(jié)點(diǎn)的比較結(jié)果向下訪問(wèn)Kdtree,直至達(dá)到葉子結(jié)點(diǎn)。
其中Q與結(jié)點(diǎn)的比較指的是將Q對(duì)應(yīng)于結(jié)點(diǎn)中的k維度上的值與中值m進(jìn)行比較,若Q(k) < m,則訪問(wèn)左子樹(shù),否則訪問(wèn)右子樹(shù)。達(dá)到葉子結(jié)點(diǎn)時(shí),計(jì)算Q與葉子結(jié)點(diǎn)上保存的數(shù)據(jù)之間的距離,記錄下最小距離對(duì)應(yīng)的數(shù)據(jù)點(diǎn),記為當(dāng)前最近鄰點(diǎn)和最小距離Distance。
(2)進(jìn)行回溯操作,該操作是為了找到離Q更近的“最近鄰點(diǎn)”。即判斷未被訪問(wèn)過(guò)的分支里是否還有離Q更近的點(diǎn),它們之間的距離小于Distance。
如果Q與其父結(jié)點(diǎn)下的未被訪問(wèn)過(guò)的分支之間的距離小于Distance,則認(rèn)為該分支中存在離P更近的數(shù)據(jù),進(jìn)入該結(jié)點(diǎn),進(jìn)行(1)步驟一樣的查找過(guò)程,如果找到更近的數(shù)據(jù)點(diǎn),則更新為當(dāng)前的最近鄰點(diǎn),并更新Distance。
如果Q與其父結(jié)點(diǎn)下的未被訪問(wèn)過(guò)的分支之間的距離大于Distance,則說(shuō)明該分支內(nèi)不存在與Q更近的點(diǎn)。
回溯的判斷過(guò)程是從下往上進(jìn)行的,直到回溯到根結(jié)點(diǎn)時(shí)已經(jīng)不存在與P更近的分支為止。
4. Kdtree的注意事項(xiàng)
a.對(duì)子空間進(jìn)行劃分時(shí),怎樣確定在哪個(gè)維度上劃分?
輪流劃分法:如果這次選擇在第i維上進(jìn)行數(shù)據(jù)劃分,那下一次就在第j(j≠i)維上進(jìn)行劃分,例如:j = (i mod k) + 1。
但是這樣忽略了不同屬性數(shù)據(jù)之間的分散程度,有的屬性值比較分散,有的屬性值比較集中。當(dāng)數(shù)據(jù)的分布在某一個(gè)維度較為集中,出現(xiàn)下圖的現(xiàn)象,第一次劃分將數(shù)據(jù)分為左右兩個(gè)子集合,安裝輪流的交替原則,第二次劃分的軸并不能很好的分割數(shù)據(jù):
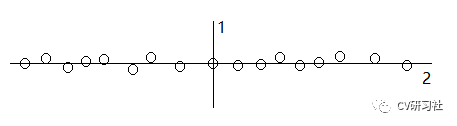
方差統(tǒng)計(jì)法:統(tǒng)計(jì)樣本在每個(gè)維度上的數(shù)據(jù)方差,選出對(duì)應(yīng)方差最大值的那個(gè)維度。因?yàn)榉讲畲笳f(shuō)明在該坐標(biāo)軸上的數(shù)據(jù)點(diǎn)較為分散。
但是理論上空間均勻分布的點(diǎn),在一個(gè)方向上分割之后,通過(guò)計(jì)算方差下一次分割就不會(huì)出現(xiàn)在這個(gè)方向上了,不過(guò)特殊情況如下:
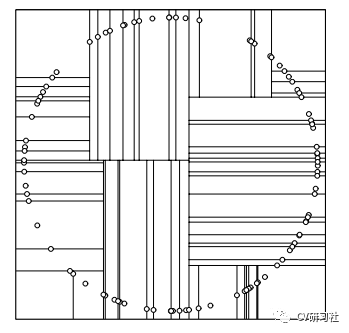
方差優(yōu)化法:初始維度的劃分依據(jù)數(shù)據(jù)方差范圍最大的那一維作為分割維度,之后也是選中這個(gè)維度的中間節(jié)點(diǎn)作為軸點(diǎn),然后進(jìn)行分割,分割出來(lái)的結(jié)果如下圖所示:
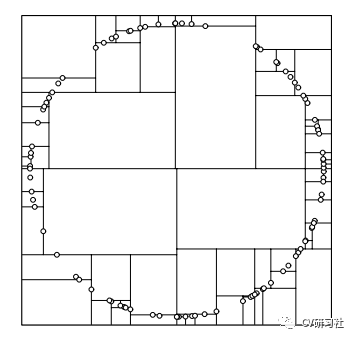
b.在某個(gè)維度上劃分時(shí),怎樣確保樹(shù)盡量平衡?
中位數(shù)法:找到該維度上數(shù)據(jù)的中位數(shù),然后將數(shù)據(jù)點(diǎn)與中位數(shù)進(jìn)行比較,得到兩個(gè)子集合的個(gè)數(shù)基本相同。
c.怎樣判斷未被訪問(wèn)的分支里有離搜索數(shù)據(jù)更近的點(diǎn)?
從幾何空間上,通過(guò)判斷以搜索數(shù)據(jù)為中心和以記錄的當(dāng)前距離為半徑的超球面與樹(shù)分支代表的超矩形之間是否相交。如下圖所示:
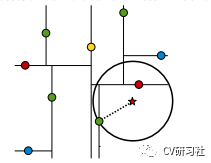
星號(hào)為搜索數(shù)據(jù),綠色的點(diǎn)為疑似最近點(diǎn),以搜索點(diǎn)和疑似最近點(diǎn)構(gòu)成的圓與所在分割區(qū)域的矩形有交集,則需要回溯根節(jié)點(diǎn)中未被訪問(wèn)的分支。
什么是Octree
1. Octree的原理
Octree是一種用于描述三維空間的樹(shù)狀數(shù)據(jù)結(jié)構(gòu)。八叉樹(shù)的每個(gè)節(jié)點(diǎn)表示一個(gè)正方體的體積元素,每個(gè)節(jié)點(diǎn)有八個(gè)子節(jié)點(diǎn),將八個(gè)子節(jié)點(diǎn)所表示的體積元素加在一起就等于父節(jié)點(diǎn)的體積。能夠很好的壓縮點(diǎn)云節(jié)省存儲(chǔ)空間。
通過(guò)對(duì)三維空間的幾何實(shí)體進(jìn)行體元剖分,每個(gè)體元具有相同的時(shí)間和空間復(fù)雜度,通過(guò)循環(huán)遞歸的劃分方法對(duì)大小為(2n?2n?2n)的三維空間的幾何對(duì)象進(jìn)行剖分,從而構(gòu)成一個(gè)具有根節(jié)點(diǎn)的方向圖。在八叉樹(shù)結(jié)構(gòu)中如果被劃分的體元具有相同的屬性,則該體元構(gòu)成一個(gè)葉節(jié)點(diǎn);否則繼續(xù)對(duì)該體元剖分成8個(gè)子立方體,依次遞剖分,對(duì)于(2n?2n?2n)大小的空間對(duì)象,最多剖分n 次,如下圖所示:
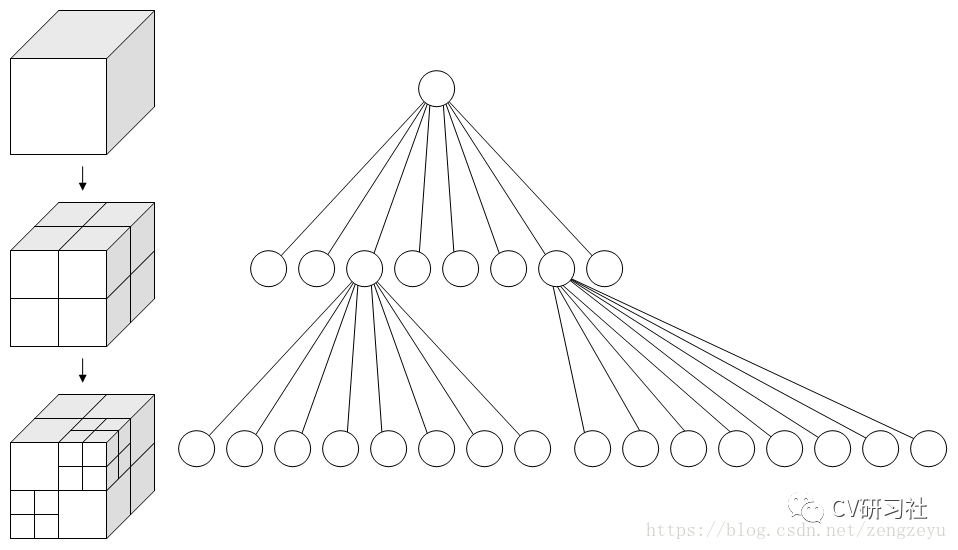
2. Octree的創(chuàng)建
(1)設(shè)定最大遞歸深度
(2)找出場(chǎng)景的最大尺寸,并以此尺寸建立第一個(gè)立方體
(3)依序?qū)挝辉貋G入能被包含且沒(méi)有子節(jié)點(diǎn)的立方體
(4)若沒(méi)有達(dá)到最大遞歸深度,就進(jìn)行細(xì)分八等份,再將該立方體所裝的單位元元素全部分擔(dān)給八個(gè)子立方體
(5)若發(fā)現(xiàn)子立方體所分配到的單位元元素?cái)?shù)量不為零且跟父立方體是一樣的,則該子立方體停止細(xì)分,因?yàn)楦鶕?jù)空間分割理論,細(xì)分的空間所得到的分配必定較少,若是一樣數(shù)目,則再怎么切數(shù)目還是一樣,會(huì)造成無(wú)窮切割的情形。
(5)重復(fù)3,直到達(dá)到最大遞歸深度。
Octree的葉子節(jié)點(diǎn)代表了分辨率最高的情況。例如分辨率設(shè)成0.01m,那么每個(gè)葉子就是一個(gè)1cm見(jiàn)方的小方塊。如下圖所示:
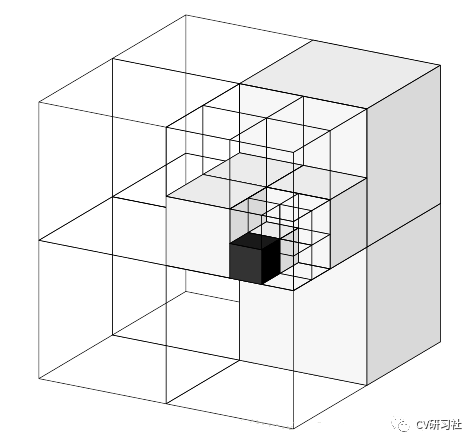
當(dāng)分辨率較高時(shí),方塊很小;分辨率較低時(shí),方塊很大。以斯坦福課程中的兔子模型為例:
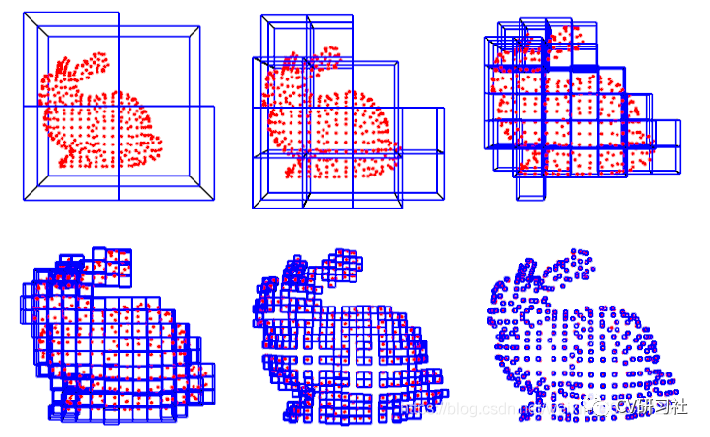
對(duì)比總結(jié)
由于三維點(diǎn)云的數(shù)據(jù)量較大,使用Kdtree和Octree進(jìn)行檢索可以較少時(shí)間消耗,確保點(diǎn)云的關(guān)聯(lián)點(diǎn)尋找和配準(zhǔn)處于實(shí)時(shí)的狀態(tài)。
Kdtree在鄰域查找上比較有優(yōu)勢(shì),但在大數(shù)據(jù)量的情況下,若劃分粒度較小時(shí),建樹(shù)的開(kāi)銷也較大,但比八叉樹(shù)靈活些。在小數(shù)據(jù)量的情況下,其搜索效率比較高,但在數(shù)據(jù)量增大的情況下,其效率會(huì)有一定的下降,一般是線性上升的規(guī)律。
Octree算法實(shí)現(xiàn)簡(jiǎn)單,但大數(shù)據(jù)量點(diǎn)云數(shù)據(jù)下,其使用比較困難的是最小粒度(葉節(jié)點(diǎn))的確定,粒度較大時(shí),有的節(jié)點(diǎn)數(shù)據(jù)量可能仍比較大,后續(xù)查詢效率仍比較低,反之,粒度較小,八叉樹(shù)的深度增加,需要的內(nèi)存空間也比較大(每個(gè)非葉子節(jié)點(diǎn)需要八個(gè)指針),效率也降低。而等分的劃分依據(jù),使得在數(shù)據(jù)重心有偏斜的情況下,受劃分深度限制,其效率不是太高。
如果將Octree和Kdtree結(jié)合起來(lái)的應(yīng)用,應(yīng)用八叉樹(shù)進(jìn)行大粒度的劃分和查找,而后使用Kdtree樹(shù)進(jìn)行細(xì)分,效率會(huì)有一定的提升,但其搜索效率變化也與數(shù)據(jù)量的變化有一個(gè)線性關(guān)系。
-
數(shù)據(jù)
+關(guān)注
關(guān)注
8文章
7246瀏覽量
91160 -
云數(shù)據(jù)
+關(guān)注
關(guān)注
0文章
118瀏覽量
16802
原文標(biāo)題:激光點(diǎn)云的組織形式
文章出處:【微信號(hào):vision263com,微信公眾號(hào):新機(jī)器視覺(jué)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
VirtualLab:光學(xué)系統(tǒng)的三維可視化
在結(jié)構(gòu)光三維成像方面DLP LightCrafter 4500如何連續(xù)投射彩色圖?
三維測(cè)量在醫(yī)療領(lǐng)域的應(yīng)用
三維測(cè)量數(shù)據(jù)處理流程
三維測(cè)量軟件的使用技巧
三維掃描與建模的區(qū)別 三維掃描在工業(yè)中的應(yīng)用
三維激光掃描儀的數(shù)據(jù)可視化技術(shù)
數(shù)字孿生三維可視化場(chǎng)景如何搭建?
基于深度學(xué)習(xí)的三維點(diǎn)云分類方法
什么是三維點(diǎn)云分割
友思特方案 基于三維點(diǎn)云實(shí)現(xiàn)PCB裝配螺絲視覺(jué)檢測(cè)

起點(diǎn),經(jīng)過(guò)點(diǎn),終點(diǎn),三點(diǎn)xyz,畫(huà)三維圓弧。
三維可視化的魅力與應(yīng)用
泰來(lái)三維 三維掃描古建筑-蘇巴什佛寺遺址數(shù)字化保護(hù)

泰來(lái)三維|三維掃描文物拍照模型制作





 三維點(diǎn)云數(shù)據(jù)的兩種結(jié)構(gòu)Kdtree和Octree
三維點(diǎn)云數(shù)據(jù)的兩種結(jié)構(gòu)Kdtree和Octree










評(píng)論