峰值電流模式控制的降壓轉(zhuǎn)換器目前在消費(fèi)電子產(chǎn)品和計(jì)算機(jī)外圍電源管理中非常流行和廣泛采用。本應(yīng)用筆記介紹了峰值電流模式降壓轉(zhuǎn)換器反饋補(bǔ)償?shù)脑O(shè)計(jì)過程,還介紹了用于電路仿真的 SIMPLIS 工具和用于定量設(shè)計(jì)的 Mathcad 數(shù)學(xué)軟件,最后通過實(shí)際測量提供了驗(yàn)證結(jié)果。
1. 峰值電流模式降壓轉(zhuǎn)換器的開環(huán)分析
峰值電流模式控制由內(nèi)部電流環(huán)路實(shí)現(xiàn),該環(huán)路由電流檢測電路 R i和斜率補(bǔ)償(鋸齒形斜坡)電路組成。檢測到的電流斜坡與鋸齒斜坡相加,然后與誤差放大器的輸出 V C進(jìn)行比較。結(jié)果用于控制 MOSFET 的導(dǎo)通時(shí)間 T ON。電路圖如圖1所示。
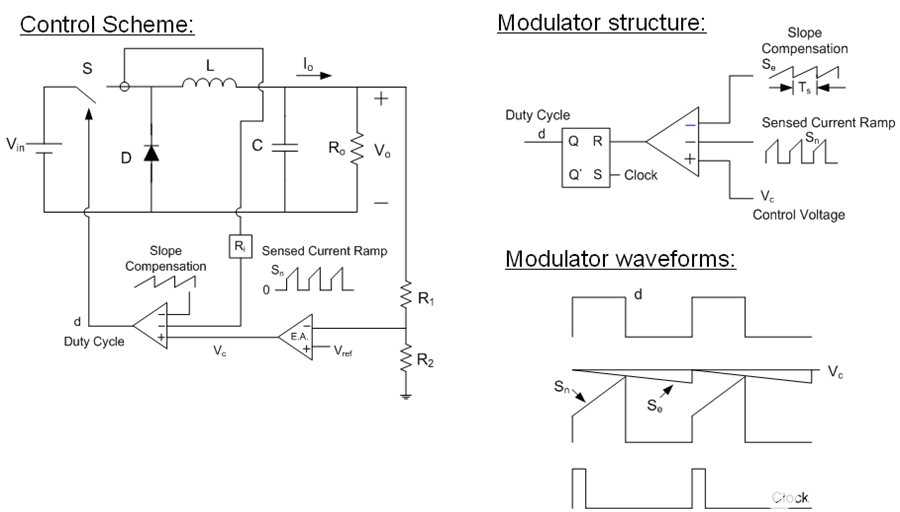
圖 1. 峰值電流模式降壓轉(zhuǎn)換器的電路圖
對于峰值電流模式,當(dāng)占空比 D 》 0.5 時(shí),可能會出現(xiàn)次諧波振蕩。在圖 2 中,T ON是 MOSFET 的導(dǎo)通時(shí)間,T S 是切換周期;虛線表示受擾動的電感電流,實(shí)線表示理想的穩(wěn)態(tài)電感電流。對于 D 《 0.5,如果開始擾動,幾個(gè)周期后它將完全阻尼;也就是說,由擾動引起的不穩(wěn)定狀態(tài)會逐漸穩(wěn)定下來。但是,對于 D 》 0.5,如果開始擾動,它將在接下來的幾個(gè)周期中繼續(xù)增加,從而使系統(tǒng)不穩(wěn)定。因此引入斜率補(bǔ)償以消除這種次諧波振蕩的風(fēng)險(xiǎn),從而使系統(tǒng)能夠保持穩(wěn)定。斜率補(bǔ)償是通過將與控制電路頻率相同的鋸齒斜坡添加到感測的電感電流斜坡來實(shí)現(xiàn)的,這樣系統(tǒng)在占空比高于 0.5 時(shí)仍然可以穩(wěn)定。
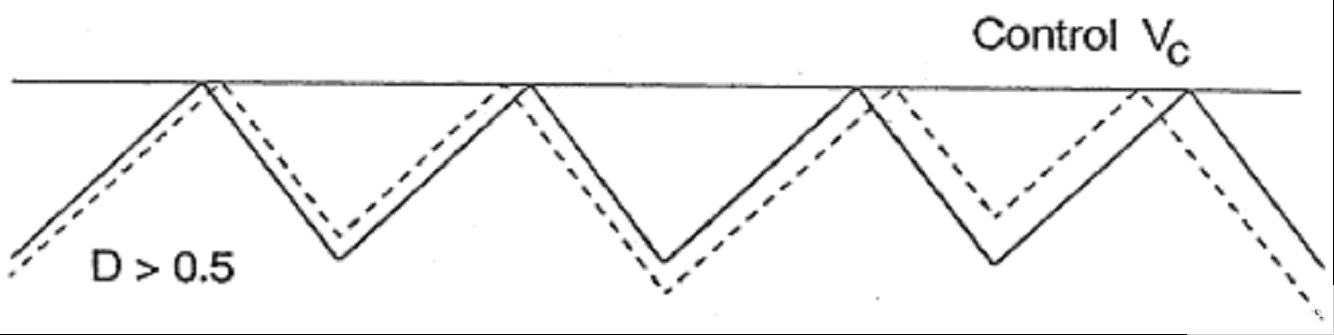
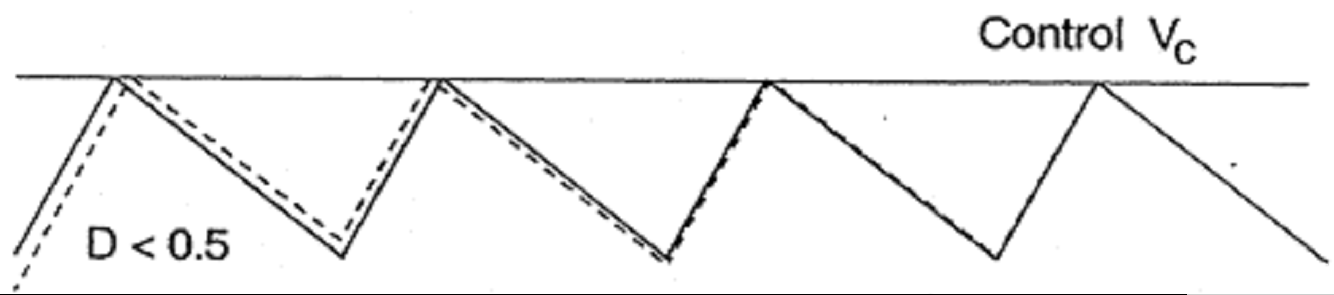
圖 2.在占空比 D 《 0.5 和 D 》 0.5 時(shí),感應(yīng)到的電感器電流以 R i斜升
本節(jié)將介紹峰值電流模式降壓轉(zhuǎn)換器 [1] [2] 的小信號模型。V. Vorperian [1] 提出的 Buck PWM 開關(guān)模型和 Raymond B. Ridley [2] 提出的用于峰值電流模式控制的小信號模型如圖 3 所示。根據(jù)該模型推導(dǎo)出的方程為應(yīng)用于峰值電流模式降壓轉(zhuǎn)換器的補(bǔ)償設(shè)計(jì)。
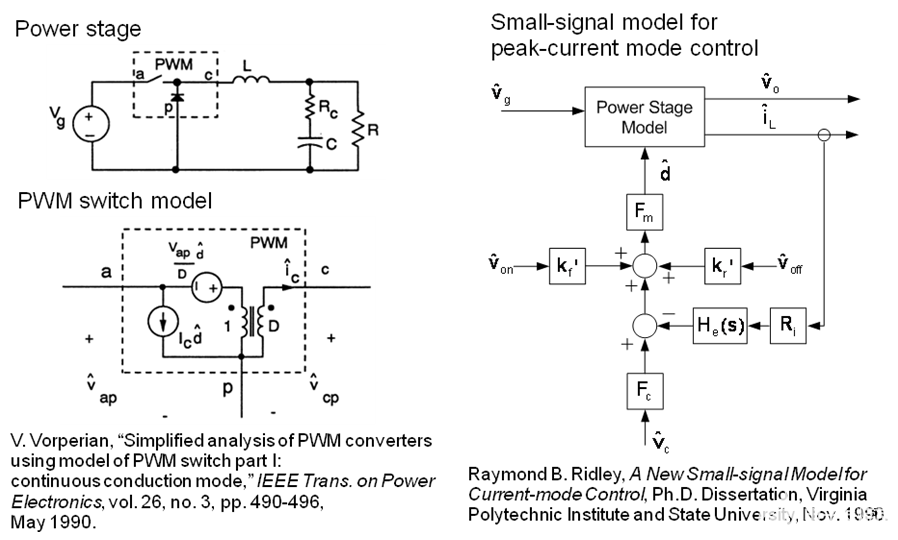
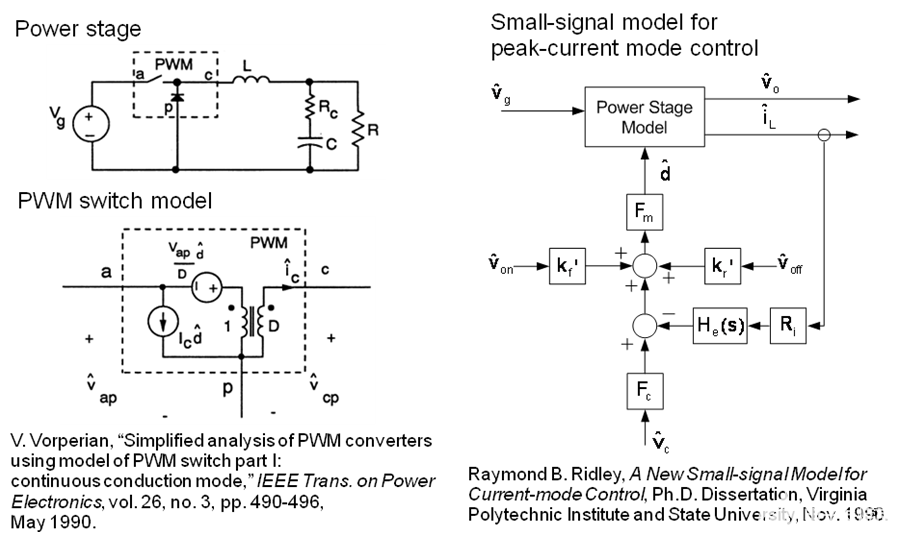
圖 3. 用于峰值電流模式控制的降壓 PWM 開關(guān)模型和小信號模型
下面列出了峰值電流模式降壓轉(zhuǎn)換器的開環(huán)傳遞函數(shù) [1]、[2]:
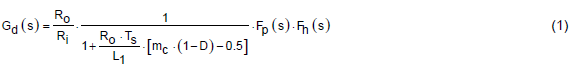
等式 (1) 中的F p (s) 主導(dǎo)了該配置的開環(huán)低頻特性,如下所示,如等式 (2) 所示,它有一個(gè)零點(diǎn)和一個(gè)極點(diǎn)。

等式 (1) 中的F h (s) 表示該配置的高頻特性,其中電流檢測變壓器 R i起重要作用。F h (s) 如下所述,如等式 (3) 所示,它具有兩個(gè)高頻極點(diǎn)。

圖 4 顯示了一個(gè)低頻主極點(diǎn)(斜率為 -20dB/十倍頻)和一個(gè)高頻雙極點(diǎn)(斜率為 -40dB/十倍頻衰減)。兩者之間的 ESR 為零來自輸出電容器的 ESR。
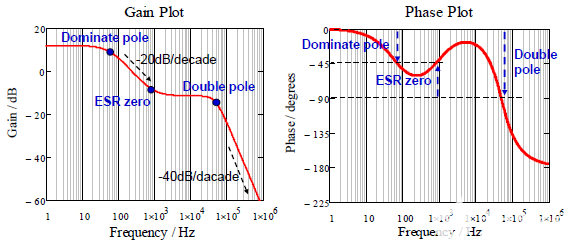
圖 4. 開環(huán)峰值電流模式降壓轉(zhuǎn)換器的波特圖
下面將逐步分析補(bǔ)償設(shè)計(jì)的方程:
首先,精確的低頻極點(diǎn)方程如下所示:
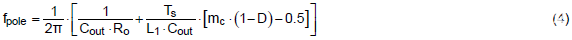
需要先進(jìn)的計(jì)算工具來計(jì)算上述方程。然而,下面列出的簡化方程是一個(gè)近似值,通過它可以快速找到極點(diǎn)。

下式為輸出電容為零:

以下等式適用于雙極點(diǎn),位于開關(guān)頻率的一半處:

通過上述公式,我們將提供一個(gè)設(shè)計(jì)示例來描述峰值電流模式降壓轉(zhuǎn)換器的重要特性。
圖 5 顯示了降壓轉(zhuǎn)換器的電路圖和相應(yīng)的電路參數(shù)。輸入電壓12Vdc,額定輸出電流3A,輸出電壓3.3V,工作頻率340kHz,電感10μH,輸出電容44μF,ESR 5mΩ。
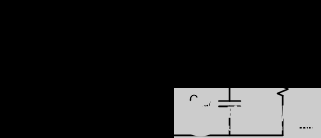
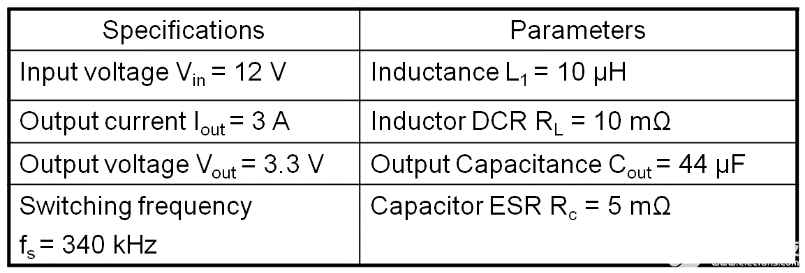
圖 5. 峰值電流模式降壓轉(zhuǎn)換器的電路圖和相應(yīng)的電路參數(shù)。
將上述參數(shù)代入式(4),得到更準(zhǔn)確的低頻一階極點(diǎn),位于4.3kHz。
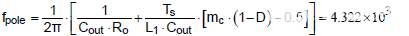
斜率補(bǔ)償因子 m c定義為
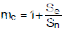
,其中 S e是添加的補(bǔ)償鋸齒斜坡的斜率,而 S n是開關(guān)打開時(shí)感測電流斜坡的斜率。
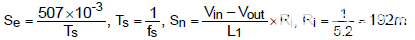
通過等式 (5),一階極點(diǎn) 3.3kHz 可以很容易地計(jì)算如下。
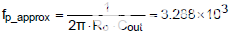
將上述參數(shù)代入式(6),可得到輸出電容ESR歸零的準(zhǔn)確位置為723kHz。
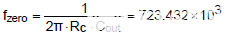
然后,通過等式(7),獲得高頻雙極點(diǎn)為 170kHz。
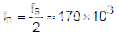
插入上述所有參數(shù)后,Mathcad 可以繪制如下波特圖。在圖 6 中,可以看出極點(diǎn)出現(xiàn)在低頻 (3.28kHz) 處,而 ESR 零 (723kHz) 出現(xiàn)在比雙極點(diǎn)更高的頻率處,因?yàn)槭褂昧溯^小的 ESR。
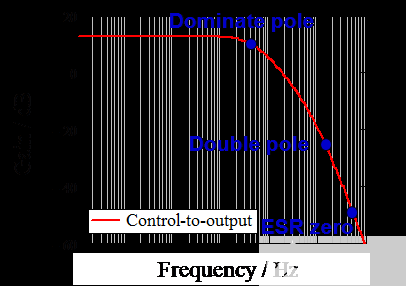
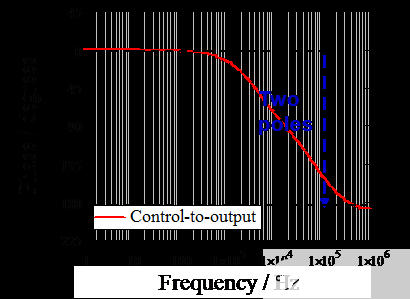
圖 6. 設(shè)計(jì)實(shí)例中開環(huán)峰值電流模式降壓轉(zhuǎn)換器的波特圖
2. 峰值電流模式降壓轉(zhuǎn)換器的補(bǔ)償設(shè)計(jì)
上一節(jié)已經(jīng)描述了峰值電流模式降壓的特性。在本節(jié)中,將研究如何補(bǔ)償峰值電流模式降壓轉(zhuǎn)換器以提高系統(tǒng)穩(wěn)定性。在圖 7 中,開環(huán)增益以紅色繪制;在低頻時(shí),直流增益很低。低頻下的低直流增益會導(dǎo)致穩(wěn)態(tài)誤差,如圖 10 所示,圖 9 顯示了具有相同帶寬和相位裕度的兩種不同直流增益的頻率響應(yīng)。對于 f 》 f c,增益曲線斜率為-40dB/decade,相位曲線斜率為-90°/decade,往往導(dǎo)致相位裕度不足,如圖8所示,進(jìn)而導(dǎo)致系統(tǒng)不穩(wěn)定。最佳閉環(huán)增益以藍(lán)色繪制。與開環(huán)增益相比,閉環(huán)增益具有以下優(yōu)點(diǎn):低頻時(shí)直流增益較高,穩(wěn)態(tài)誤差可以最小化,如圖 10 所示,當(dāng) f 》 f c時(shí),增益為-20dB/decade 的斜率和 -45°/decade 的相位,如圖 7 所示,從而提高相位裕度 (PM)。

圖 7. 開環(huán)和閉環(huán)波特圖的比較
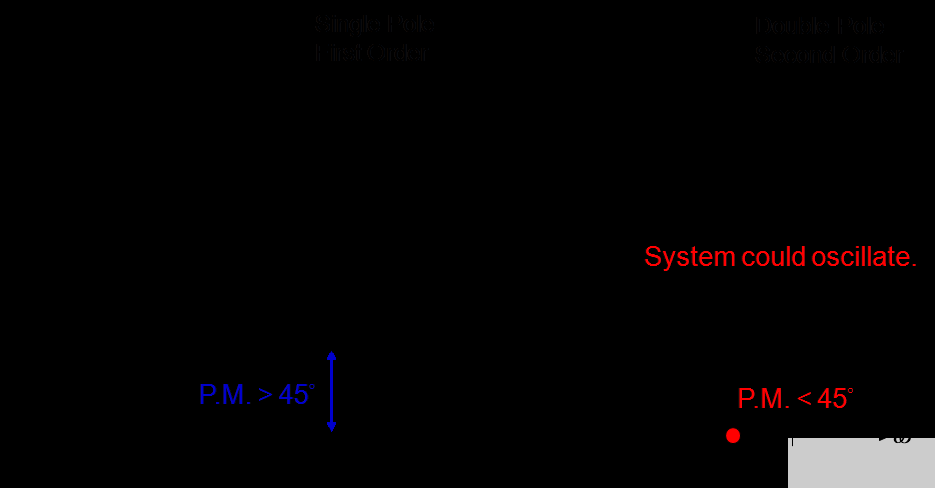
圖 8. 單極與雙極
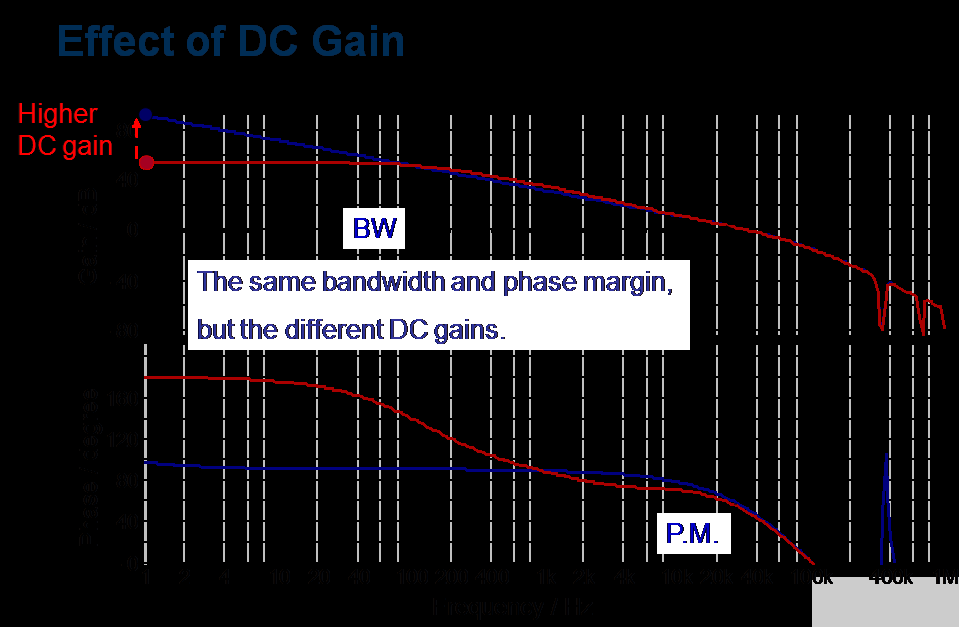
圖 9. 具有相同帶寬和相位裕度的不同 DC 增益
在圖 10 中,可以看出負(fù)載調(diào)節(jié)率越高,直流增益越好,而直流增益越低,負(fù)載調(diào)節(jié)率越差。
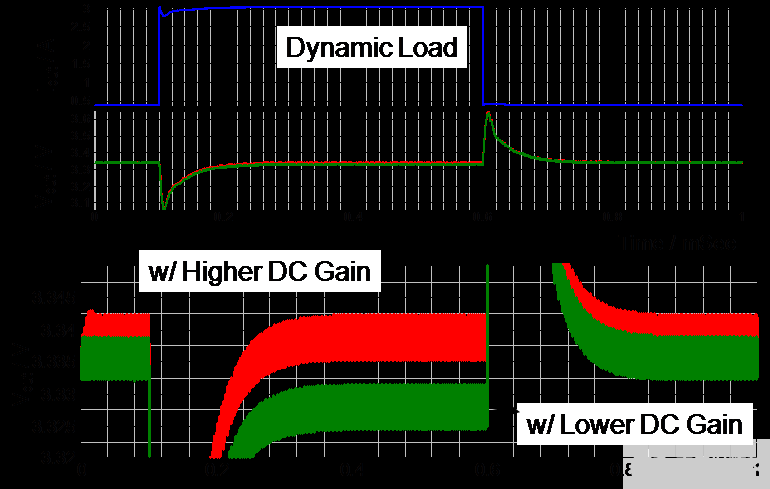
圖 10. 直流增益對負(fù)載調(diào)節(jié)的影響
基于以上對系統(tǒng)性能電路參數(shù)的分析,補(bǔ)償器需要一個(gè)零點(diǎn)來抵消峰值電流模式降壓轉(zhuǎn)換器的低頻極點(diǎn),如圖 11 所示,這樣增益曲線將是在交叉頻率的斜率為 -20dB / 十倍頻,從而獲得更好的相位裕度。在高頻下,高頻補(bǔ)償器極點(diǎn)可以幫助濾除高頻噪聲。
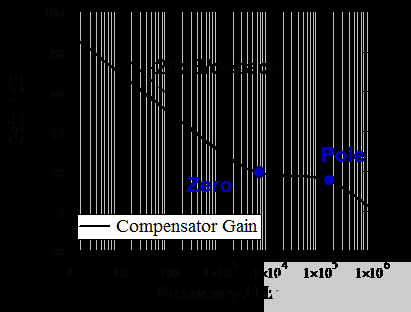
圖 11. 補(bǔ)償器提供零和極點(diǎn)
下面以 GM 型補(bǔ)償器為例。由于 GM 型補(bǔ)償器有一個(gè)零和兩個(gè)極點(diǎn),因此非常適合補(bǔ)償峰值電流模式降壓轉(zhuǎn)換器。可以從 R gm和 C comp獲得第一個(gè)極點(diǎn),從 R comp和 C gm獲得另一個(gè)極點(diǎn),從 R comp 和 C comp獲得零。
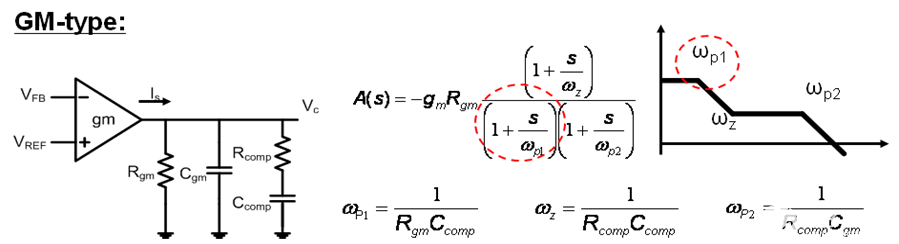
圖 12. GM 型補(bǔ)償器
補(bǔ)償器設(shè)計(jì)程序:
第一步:
設(shè)置交叉頻率(即帶寬)。在上面的例子中,工作頻率為 340kHz,帶寬通常設(shè)置為工作頻率的 1/10。

第 2 步:
將補(bǔ)償器置零以取消峰值電流模式降壓拓?fù)涞臉O點(diǎn)。

步驟 3:
補(bǔ)償器極點(diǎn)設(shè)置為 ESR 零和工作頻率的 1/2 之間的較低頻率。在本例中,工作頻率的 1/2 低于 ESR 零,因此將補(bǔ)償器極點(diǎn)設(shè)置為工作頻率的 1/2。

步驟 4:
通過 Mathcad,48° 的相位裕度可以通過以下等式獲得。通常為了穩(wěn)定,相位裕度應(yīng)大于 45°。
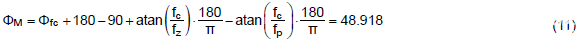
第 5 步:
根據(jù)等式 (12),由補(bǔ)償器在交叉頻率處增加的直流增益可計(jì)算為 17.4dB。
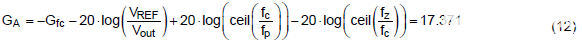
第6步:
本例中補(bǔ)償器的參數(shù),如R comp = 5.9kΩ,C comp = 6.23nF,C gm = 158pF,都可以得到如下。
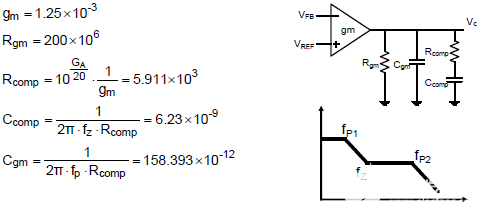
Step 7 :
將上述所有數(shù)字代入式(13),然后將等式輸入Mathcad,即可繪制出補(bǔ)償器的Bode圖,如圖13所示。

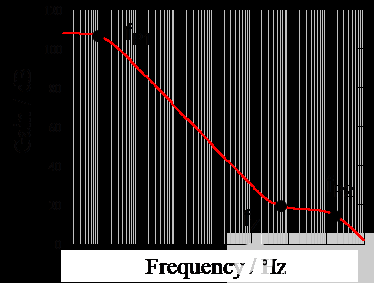
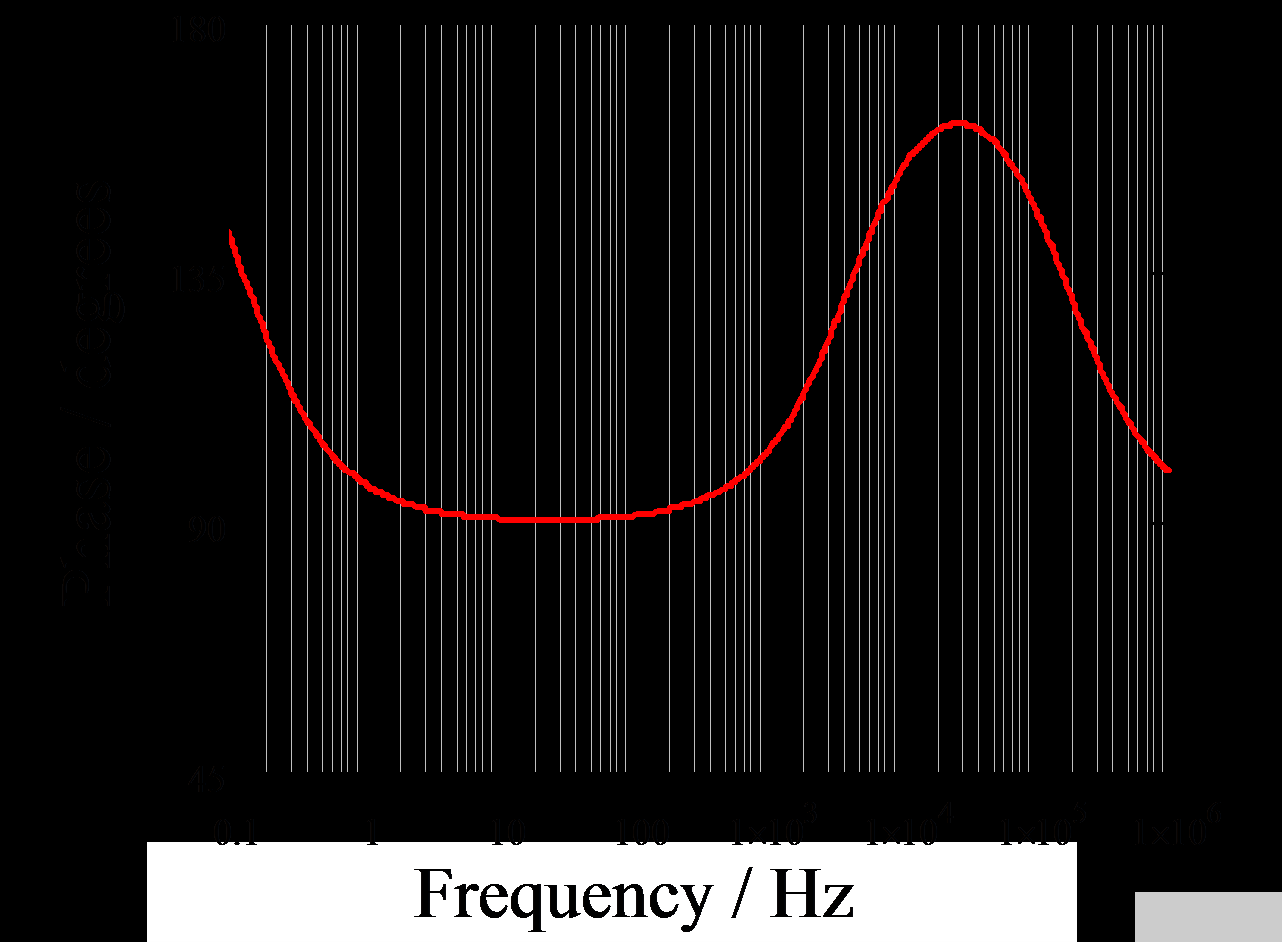
圖 13. 補(bǔ)償器的波特圖
3. 峰值電流模式降壓轉(zhuǎn)換器的閉環(huán)分析
在本節(jié)中,SIMPLIS 工具用于模擬峰值電流模式降壓轉(zhuǎn)換器并證實(shí)閉環(huán)頻率響應(yīng)分析。SIMPLIS 原理圖如圖 14 所示。該電流模式降壓轉(zhuǎn)換器的閉環(huán)包含一個(gè)電流傳感器、一個(gè)補(bǔ)償器和一個(gè)斜率補(bǔ)償電路。
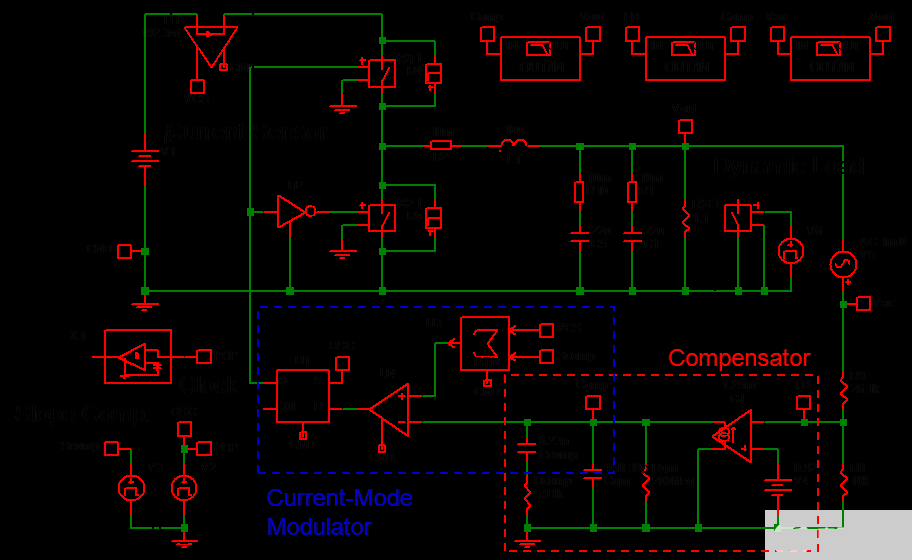
圖 14. SIMPLIS 仿真示意圖(閉環(huán)峰值電流模式降壓轉(zhuǎn)換器)
在圖 15 中,上一節(jié)的方程(紅線)由 Mathcad 繪制,并與圖 14 中 SIMPLIS 原理圖的仿真結(jié)果(藍(lán)點(diǎn))進(jìn)行了驗(yàn)證。表明仿真結(jié)果與解析結(jié)果非常吻合,由 Mathcad 導(dǎo)出,帶寬和相位裕度分別為 34kHz 和 48.9°。
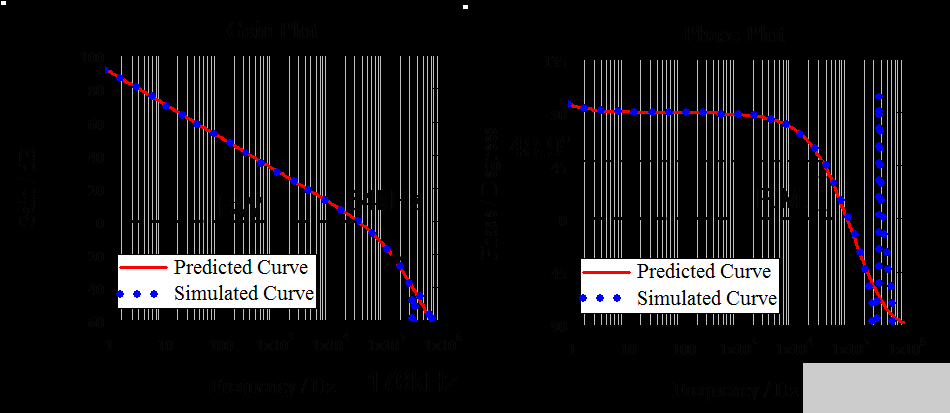
圖 15. 理論分析與 Matchcad 和 SIMPLIS 仿真的比較
圖 16 展示了補(bǔ)償器可以提供的好處。首先,補(bǔ)償器(黑色虛線)增強(qiáng)了低頻范圍內(nèi)的直流增益。開環(huán)響應(yīng)(紅線)與補(bǔ)償器響應(yīng)(黑色虛線)相結(jié)合,形成閉環(huán)響應(yīng)(藍(lán)線)。其次,補(bǔ)償器增加了帶寬,如圖 16 所示,藍(lán)色的交叉頻率大于紅色的交叉頻率。第三,補(bǔ)償器增加了一個(gè)高頻極點(diǎn),提高了高頻抗噪能力(在高頻下,藍(lán)線比紅線下降得快)。第四,補(bǔ)償器的零有助于實(shí)現(xiàn)足夠的相位裕度。
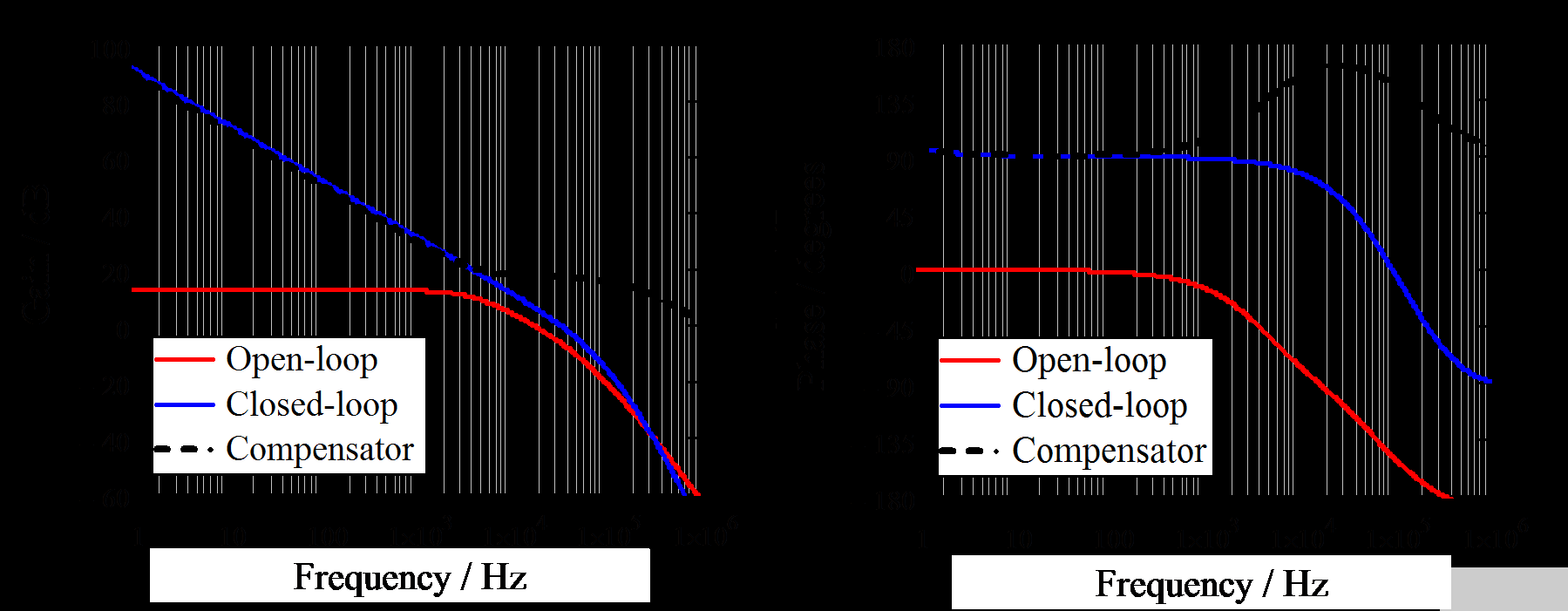
圖 16. 開環(huán)和閉環(huán)的比較
圖 17 給出了實(shí)際測量設(shè)置,將交流擾動信號注入點(diǎn) R。通過測量輸出(A 點(diǎn))與輸入(R 點(diǎn))的關(guān)系,可以獲得增益和相位圖。從圖 17 的右側(cè)圖中,測量結(jié)果(綠線)與分析結(jié)果(紅線)非常吻合。
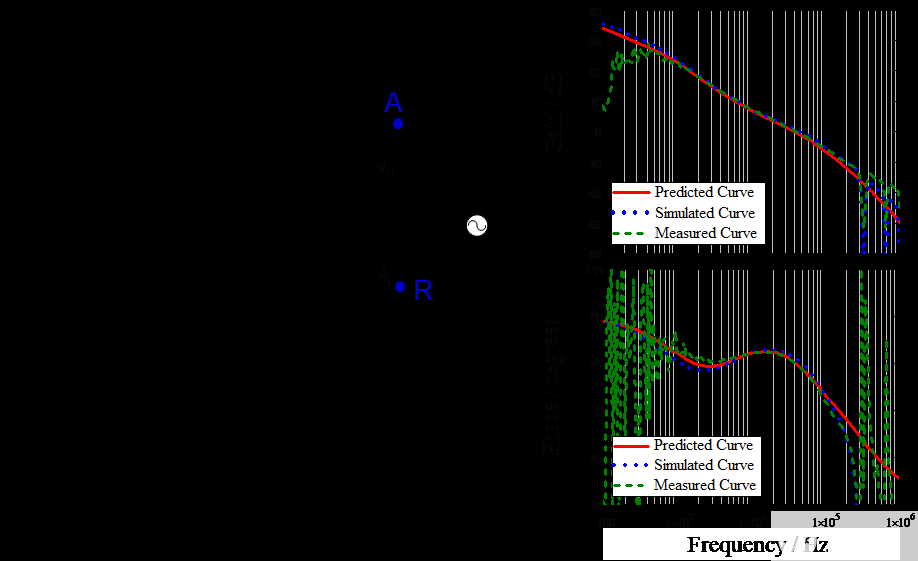
圖 17. 實(shí)驗(yàn)結(jié)果驗(yàn)證閉環(huán)頻率響應(yīng)
4。結(jié)論
在低頻下,開環(huán)峰值電流模式降壓轉(zhuǎn)換器仍然是單極點(diǎn)系統(tǒng),因?yàn)榄h(huán)路控制是通過僅將電流信號注入環(huán)路來實(shí)現(xiàn)的。
它的補(bǔ)償器易于設(shè)計(jì)。零補(bǔ)償器旨在消除降壓轉(zhuǎn)換器的主極點(diǎn),以實(shí)現(xiàn)系統(tǒng)穩(wěn)定性。
為了保證足夠的相位裕度,設(shè)計(jì)目標(biāo)是增益曲線在通過交叉頻率時(shí)在斜率-20dB/十倍頻。
-
降壓轉(zhuǎn)換器
+關(guān)注
關(guān)注
7文章
1751瀏覽量
87122 -
峰值電流
+關(guān)注
關(guān)注
0文章
220瀏覽量
12176 -
Mathcad
+關(guān)注
關(guān)注
3文章
17瀏覽量
11798
發(fā)布評論請先 登錄
峰值電流模式控制設(shè)計(jì)
小技巧:電流模式控制簡化了對降壓LED穩(wěn)壓器的補(bǔ)償
改進(jìn)峰值電流模式控制的方法
TI電源技巧:電流模式控制簡化了對降壓LED穩(wěn)壓器的補(bǔ)償
降壓轉(zhuǎn)換器的基本工作及不連續(xù)模式和續(xù)模式
技術(shù)貼:如何在峰值電流模式控制電壓環(huán)路補(bǔ)償
MT-059: 補(bǔ)償輸入電容對電流電壓轉(zhuǎn)換器所用電壓反饋和電流反饋型運(yùn)算放大器的影響

采用數(shù)字斜率補(bǔ)償的峰值電流控制ZVS全橋轉(zhuǎn)換器
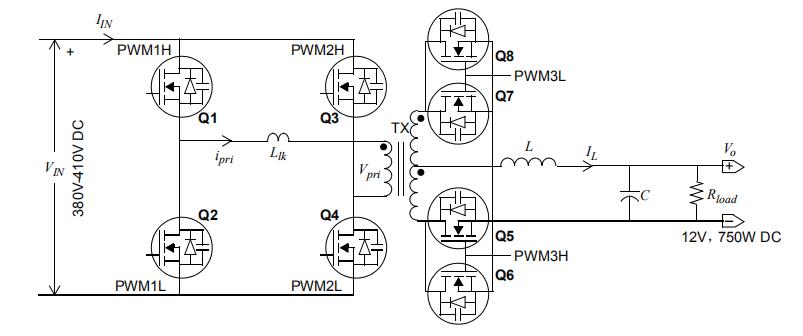
使用C2000 Real-t的峰值電流模式控制PSFB轉(zhuǎn)換器參考設(shè)計(jì)
使用峰值電流模式控制器設(shè)計(jì)升壓轉(zhuǎn)換器
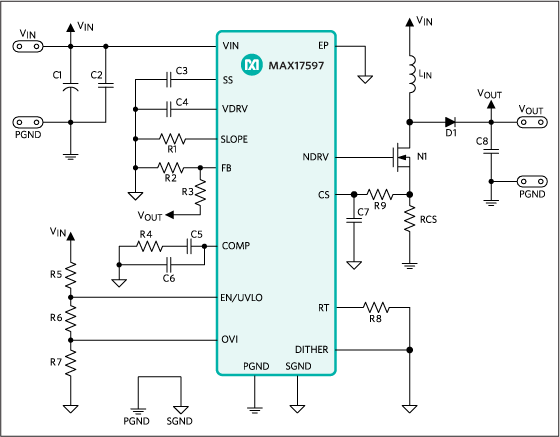
電流模式降壓轉(zhuǎn)換器的建模與控制

用于USB應(yīng)用的峰值電流限制降壓轉(zhuǎn)換器TPS62250數(shù)據(jù)表

PCM(峰值電流模式)降壓轉(zhuǎn)換器中的功率級增益和斜率補(bǔ)償測量

電流模式轉(zhuǎn)換器的建模、分析和補(bǔ)償






 峰值電流模式降壓轉(zhuǎn)換器反饋補(bǔ)償?shù)脑O(shè)計(jì)過程
峰值電流模式降壓轉(zhuǎn)換器反饋補(bǔ)償?shù)脑O(shè)計(jì)過程










評論