Clarke變換是“矢量坐標變換”中的一種變換方式,在永磁同步電機中,電動機的定子磁場是由定子的三相繞組的磁動勢產生的,根據電動機旋轉磁場理論就知,向對稱的三相繞組中通以對稱的三相正弦電流時,就會產生合成的磁動勢,并以w的速度在空間中旋轉。所以,為了簡化交流電機的分析方法,Clarke提出了一種以電機定子為靜止參考系的電機參數變換分析方式,即依據功率不變和磁勢不變的原理,將定子三相物理量從三維坐標轉換到二維坐標,簡稱3S/2S變換,其中S表示靜止。
在PMSM中建立合適的坐標系
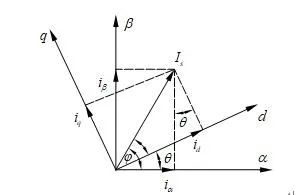
圖1-1中兩個坐標系,其中ABC是PMSM靜止坐標系,另一個坐標系是PMSM經過Clarke要變換后的坐標系:
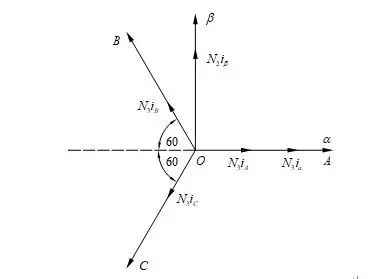
圖1-1 Clarke坐標變換示意圖
圖1-1中PMSM三相繞組每相的有效線圈匝數為N3,兩相繞組每相有效線圈匝數為N2,兩種坐標系中每相的磁動勢均為有效線圈匝數與該相電流的乘積。
原理分析
矢量坐標變換就是用磁勢或者電流空間矢量來描述等效的三相磁場、兩相磁場和旋轉直流磁場,并對它們進行坐標變換。因此矢量坐標變化必須要遵循以下兩個原則:
1、變換前后電流所產生的旋轉磁場等效;
2、變換前后兩系統的電動機功率不發生變化。
根據矢量變換原則,Clarke變換前后的磁場應該完全等效,即合成的磁勢矢量分別在兩個坐標系坐標軸上的投影應該相等。設磁動勢是正弦分布的,當三相總磁動勢與兩相總磁動勢相等時,兩套繞組瞬時磁動勢在兩相坐標系上的投影都應相等。
因此根據圖1-1可以得出磁勢守恒的式子為:
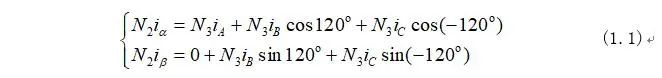
將式(1.1)變形又可化為矩陣形式為:
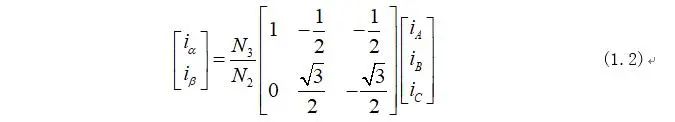
因為式(1.2)中矩陣不是方陣不能求的逆矩陣,所以需要引入新變量零軸電流:
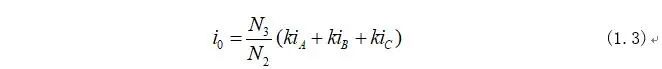
將式(1.3)和式(1.2)合并可以得到兩相坐標系方程為:

所以定義Clarke矩陣為:
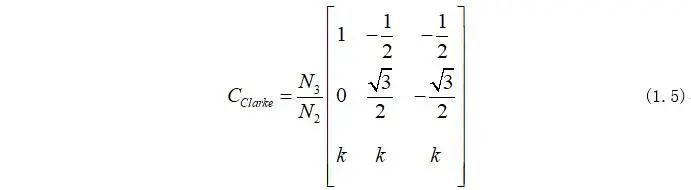
Clarke最終表達形式
其中Clarke矩陣的轉置矩陣為:
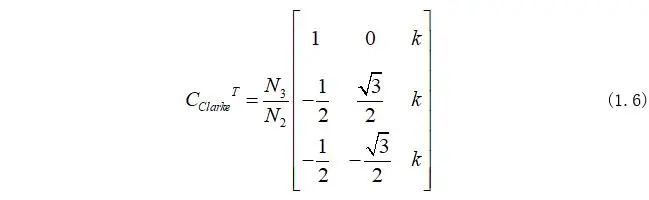
Clarke矩陣的逆矩陣為:
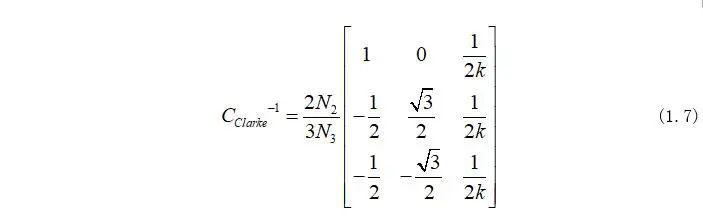
在Clarke變換下需要保證發電機的輸出功率在變換前后不能發生變換,因此計算公式為:
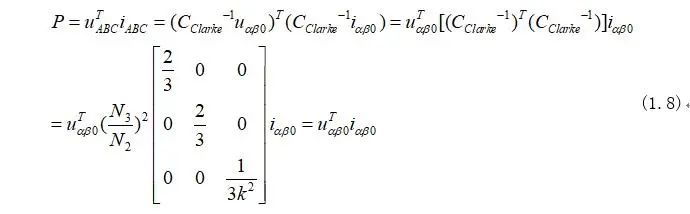
由式(1.8)可知,為了確保變換前后輸出功率不變化,可以其中參數求得:
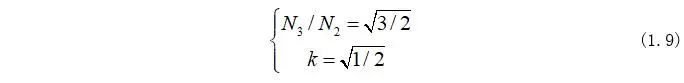
因此,Clarke變換式為:
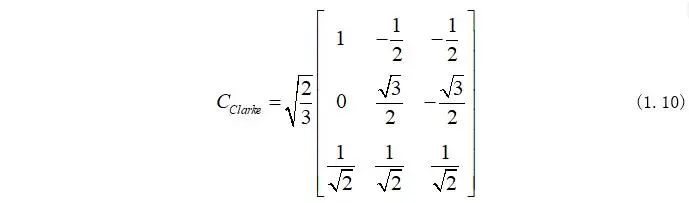
如果忽略零軸變量,那么Clarke變換式又可化為:
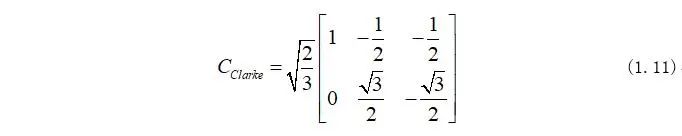
Clarke如何應用
如何得到永磁同步電機在靜止兩相坐標的電機電壓方程?
永磁同步電機的定子電壓方程在三相靜止坐標系下為:
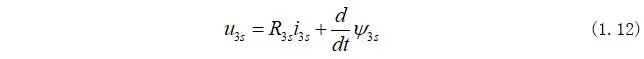
將式(1.12)乘以Clarke矩陣可以得到永磁同步電機在兩相靜止坐標系下的電機電壓方程為:
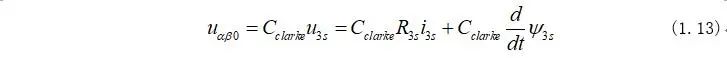
-
電動機
+關注
關注
75文章
4158瀏覽量
98521 -
坐標系
+關注
關注
0文章
29瀏覽量
7472 -
PMSM
+關注
關注
14文章
248瀏覽量
42613 -
坐標變換
+關注
關注
0文章
19瀏覽量
6955 -
CLARKE
+關注
關注
0文章
6瀏覽量
6800
發布評論請先 登錄
MATLAB建立和控制圖形窗口和坐標系命令
vision Assitant 建立坐標系(模板匹配)
labwindows/cvi中,請問如何在canvas控件上畫一個扇形的極坐標系?
A、B、C三相坐標系中PMSM數學模型定子電壓方程
PMSM的坐標系和數學模型
如何在PMSM中建立合適的坐標系(二)
自動駕駛各個坐標系






 如何在PMSM中建立合適的坐標系(一)
如何在PMSM中建立合適的坐標系(一)












評論