筆者簡述: 這篇論文主要還是在于深度估計(jì)這塊,深度估計(jì)由于硬件設(shè)備的不同是有很多方法的,雙目,RGBD,激光雷達(dá),單目,其中最難大概就是單目了。在該論文中作者利用BA導(dǎo)出的信息矩陣來估計(jì)深度和深度的不確定性,利用深度的不確定性對3D體積重建進(jìn)行加權(quán)三維重建,在精度和實(shí)時性方面都得到了不錯的結(jié)果,值得關(guān)注。
摘要
我們提出了一種利用深度密集單目 SLAM和快速不確定性傳播從圖像重建 3D 場景的新方法。所提出的方法能夠密集、準(zhǔn)確、實(shí)時地 3D 重建場景,同時對來自密集單目 SLAM 的極其嘈雜的深度估計(jì)具有魯棒性。不同于以前的方法,要么使用臨時深度過濾器,要么從 RGB-D 相機(jī)的傳感器模型估計(jì)深度不確定性,我們的概率深度不確定性直接來自SLAM中底層BA問題的信息矩陣。
我們表明,由此產(chǎn)生的深度不確定性為體積融合的深度圖加權(quán)提供了極好的信號。如果沒有我們的深度不確定性,生成的網(wǎng)格就會很嘈雜并且?guī)в袀斡埃覀兊姆椒〞梢粋€精確的 3D 網(wǎng)格,并且偽影要少得多。我們提供了具有挑戰(zhàn)性的 Euroc 數(shù)據(jù)集的結(jié)果,并表明我們的方法比直接融合單目 SLAM 的深度提高了 92% 的準(zhǔn)確性,與最佳競爭方法相比提高了 90%
1. 簡介
單目圖像的 3D 重建仍然是最困難的計(jì)算機(jī)視覺問題之一。僅從圖像實(shí)時實(shí)現(xiàn) 3D 重建就可以實(shí)現(xiàn)機(jī)器人、測量和游戲中的許多應(yīng)用,例如自動駕駛汽車、作物監(jiān)測和增強(qiáng)現(xiàn)實(shí)。 雖
然許多 3D 重建解決方案基于 RGB-D 或激光雷達(dá)傳感器,但單目圖像的場景重建提供了更方便的解決方案。
RGB-D 相機(jī)在某些條件下可能會失效,例如在陽光下,激光雷達(dá)仍然比單目 RGB 相機(jī)更重、更昂貴。或者,立體相機(jī)將深度估計(jì)問題簡化為一維視差搜索,但依賴于在實(shí)際操作中容易出現(xiàn)錯誤校準(zhǔn)的相機(jī)的精確校準(zhǔn)。相反,單目相機(jī)便宜、重量輕,代表了最簡單的傳感器配置來校準(zhǔn)。
不幸的是,由于缺乏對場景幾何形狀的明確測量,單目 3D 重建是一個具有挑戰(zhàn)性的問題。
盡管如此,最近通過利用深度學(xué)習(xí)方法在基于單眼的 3D 重建方面取得了很大進(jìn)展。鑒于深度學(xué)習(xí)目前在光流 [23] 和深度 [29] 估計(jì)方面取得了最佳性能,因此大量工作已嘗試將深度學(xué)習(xí)模塊用于 SLAM。例如,使用來自單目圖像 [22]、多幅圖像的深度估計(jì)網(wǎng)絡(luò),如多視圖立體 [10],或使用端到端神經(jīng)網(wǎng)絡(luò) [3]。
然而,即使有了深度學(xué)習(xí)帶來的改進(jìn),由此產(chǎn)生的重建也容易出現(xiàn)錯誤和偽影,因?yàn)樯疃葓D大部分時間都是嘈雜的并且有異常值。
在這項(xiàng)工作中,我們展示了如何從使用密集單目 SLAM 時估計(jì)的嘈雜深度圖中大幅減少 3D 重建中的偽影和不準(zhǔn)確性。為實(shí)現(xiàn)這一點(diǎn),我們通過根據(jù)概率估計(jì)的不確定性對每個深度測量值進(jìn)行加權(quán)來體積融合深度圖。
與以前的方法不同,我們表明,在單目 SLAM 中使用從BA問題的信息矩陣導(dǎo)出的深度不確定性導(dǎo)致令人驚訝的準(zhǔn)確 3D 網(wǎng)格重建。我們的方法在映射精度方面實(shí)現(xiàn)了高達(dá) 90% 的改進(jìn),同時保留了大部分場景幾何。
貢獻(xiàn):我們展示了一種體積融合密集深度圖的方法,該深度圖由密集 SLAM 中的信息矩陣導(dǎo)出的不確定性加權(quán)。我們的方法使場景重建達(dá)到給定的最大可容忍不確定性水平。
與競爭方法相比,我們可以以更高的精度重建場景,同時實(shí)時運(yùn)行,并且僅使用單目圖像。我們在具有挑戰(zhàn)性的 EuRoC 數(shù)據(jù)集中實(shí)現(xiàn)了最先進(jìn)的 3D 重建性能。
圖 1.(左)原始 3D 點(diǎn)云通過反向投影逆深度圖從密集單眼 SLAM 生成,沒有過濾或后處理。 (右)深度圖的不確定性感知體積融合后估計(jì)的 3D 網(wǎng)格。
盡管深度圖中有大量噪聲,但使用我們提出的方法重建的 3D 網(wǎng)格是準(zhǔn)確和完整的。
EuRoC V2 01 數(shù)據(jù)集。
2. 相關(guān)工作
我們回顧了兩個不同工作領(lǐng)域的文獻(xiàn):密集 SLAM 和深度融合。
2.1.Dense SLAM
實(shí)現(xiàn)Dense SLAM 的主要挑戰(zhàn)是(i)由于要估計(jì)的深度變量的剪切量導(dǎo)致的計(jì)算復(fù)雜性,以及(ii)處理模糊或缺失的信息以估計(jì)場景的深度,例如無紋理表面或混疊圖像。 從歷史上看,第一個問題已通過解耦姿態(tài)和深度估計(jì)而被繞過。
例如,DTAM [12] 通過使用與稀疏 PTAM [9] 相同的范例來實(shí)現(xiàn)Dense SLAM,它以解耦的方式首先跟蹤相機(jī)姿勢,然后跟蹤深度。第二個問題通常也可以通過使用提供明確深度測量的 RGB-D 或激光雷達(dá)傳感器或簡化深度估計(jì)的立體相機(jī)來避免。
盡管如此,最近對Dense SLAM 的研究在這兩個方面取得了令人矚目的成果。為了減少深度變量的數(shù)量,CodeSLAM [3] 優(yōu)化了從圖像推斷深度圖的自動編碼器的潛在變量。通過優(yōu)化這些潛在變量,問題的維數(shù)顯著降低,而生成的深度圖仍然很密集。
Tandem [10] 能夠通過在單眼深度估計(jì)上使用預(yù)訓(xùn)練的 MVSNet 式神經(jīng)網(wǎng)絡(luò),然后通過執(zhí)行幀到模型的光度跟蹤來解耦姿態(tài)/深度問題,從而僅使用單眼圖像重建 3D 場景。 Droid-SLAM [24] 表明,通過采用最先進(jìn)的密集光流估計(jì)架構(gòu) [23] 來解決視覺里程計(jì)問題,有可能在各種情況下取得有競爭力的結(jié)果具有挑戰(zhàn)性的數(shù)據(jù)集(例如 Euroc [4] 和 TartanAir [25] 數(shù)據(jù)集),即使它需要全局束調(diào)整以優(yōu)于基于模型的方法。
Droid-SLAM 通過使用下采樣深度圖避免了維度問題,隨后使用學(xué)習(xí)的上采樣運(yùn)算符對深度圖進(jìn)行上采樣。最后,有無數(shù)的作品避免了上述的維度和歧義問題,但最近已經(jīng)取得了改進(jìn)的性能。例如,iMap [21] 和 Nice-SLAM [31] 可以通過解耦姿態(tài)和深度估計(jì)以及使用 RGB-D 圖像來構(gòu)建精確的 3D 重建,并通過使用神經(jīng)輻射場 [11] 實(shí)現(xiàn)光度精確重建.鑒于這些工作,我們可以期待未來學(xué)習(xí)的Dense SLAM 變得更加準(zhǔn)確和穩(wěn)健。
不幸的是,我們還不能從隨意的圖像集合中獲得像素完美的深度圖,將這些深度圖直接融合到體積表示中通常會導(dǎo)致偽影和不準(zhǔn)確。我們的工作利用 Droid-SLAM [24] 來估計(jì)每個關(guān)鍵幀的極其密集(但非常嘈雜)的深度圖(參見圖 1 中的左側(cè)點(diǎn)云),我們通過根據(jù)深度的不確定性對深度進(jìn)行加權(quán),成功地將其融合到體積表示中,估計(jì)為邊際協(xié)方差。
2.2.深度融合
絕大多數(shù) 3D 重建算法都基于將深度傳感器提供的深度圖融合到體積圖 [13、15、17] 中。因此,大多數(shù)使用體積表示的文獻(xiàn)都專注于研究獲得更好深度圖的方法,例如后處理技術(shù),或融合深度時要使用的加權(quán)函數(shù) [5、13、14、28]。大多數(shù)文獻(xiàn),通過假設(shè)深度圖來自傳感器,專注于傳感器建模。或者,在使用深度學(xué)習(xí)時,類似的方法是讓神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)權(quán)重。例如,RoutedFusion [26] 和 NeuralFusion [27] 學(xué)習(xí)從 RGB-D 掃描中去噪體積重建。
在我們的例子中,由于深度圖是通過密集BA估計(jì)的,我們建議使用估計(jì)深度的邊際協(xié)方差直接融合深度圖。這在計(jì)算上很難做到,因?yàn)樵贒ense SLAM 中,每個關(guān)鍵幀的深度數(shù)可能與幀中的像素總數(shù)一樣高 (≈ 105)。我們在下面展示了我們?nèi)绾瓮ㄟ^利用信息矩陣的塊稀疏結(jié)構(gòu)來實(shí)現(xiàn)這一點(diǎn)。
3. 方法
我們方法的主要思想是將由概率不確定性加權(quán)的極其密集但嘈雜的深度圖融合到體積圖中,然后提取具有給定最大不確定性界限的 3D 網(wǎng)格。為實(shí)現(xiàn)這一目標(biāo),我們利用 Droid-SLAM 的公式來生成姿態(tài)估計(jì)和密集深度圖,并將其擴(kuò)展為生成密集不確定性圖。 我們將首先展示如何從基礎(chǔ)BA問題的信息矩陣中有效地計(jì)算深度不確定性。然后,我們提出了我們的融合策略以生成概率合理的體積圖。最后,我們展示了如何在給定的最大不確定性范圍內(nèi)從體積中提取網(wǎng)格。
3.1.密集單目 SLAM
其核心,經(jīng)典的基于視覺的逆深度間接 SLAM 解決了束調(diào)整 (BA) 問題,其中 3D 幾何被參數(shù)化為每個關(guān)鍵幀的一組(逆)深度。這種結(jié)構(gòu)的參數(shù)化導(dǎo)致了一種解決密集 BA 問題的極其有效的方法,可以將其分解為熟悉的箭頭狀塊稀疏矩陣,其中相機(jī)和深度按順序排列: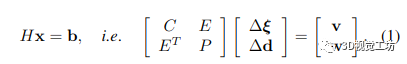
其中 H 是 Hessian 矩陣,C 是塊相機(jī)矩陣,P 是對應(yīng)于點(diǎn)的對角矩陣(每個關(guān)鍵幀每個像素一個逆深度)。我們用 Δξ 表示 SE(3) 中相機(jī)姿態(tài)的李代數(shù)的增量更新,而 Δd 是每像素逆深度的增量更新。
為了解決 BA 問題,首先計(jì)算 Hessian H 相對于 P 的 Schur 補(bǔ)碼(表示為 H/P )以消除逆深度變量: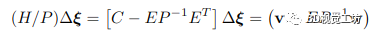
鑒于 P ?1 包含可以并行執(zhí)行的每個對角元素的逐元素求逆,可以快速計(jì)算 Schur 補(bǔ)碼,因?yàn)?P 是一個大的對角矩陣 生成的矩陣 (H/P ) 稱為縮減相機(jī)矩陣。方程式中的方程組。 (2) 僅取決于關(guān)鍵幀姿勢。因此,我們首先使用 (H/P ) = LLT 的 Cholesky 分解求解姿勢,使用前代然后后代。然后使用生成的姿態(tài)解 Δξ 來求解逆深度圖 Δd,如下所示: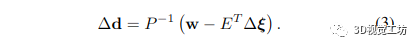
盡管如此,為了對實(shí)時 SLAM 進(jìn)行足夠快的推理,逆深度圖的估計(jì)分辨率低于原始圖像的 1/8,在我們的例子中為 69×44 像素(Euroc 數(shù)據(jù)集的原始分辨率為 752×480,這我們首先下采樣到 512×384)。一旦解決了這個低分辨率深度圖,學(xué)習(xí)的上采樣操作(首先在 [23] 中顯示用于光流估計(jì),并在 Droid-SLAM 中使用)恢復(fù)全分辨率深度圖。
這使我們能夠有效地重建與輸入圖像具有相同分辨率的密集深度圖 使用高分辨率深度圖解決相同的 BA 問題對于實(shí)時 SLAM 來說是非常昂貴的,深度不確定性的計(jì)算進(jìn)一步加劇了這個問題。
我們相信這就是為什么其他作者沒有使用從 BA 導(dǎo)出的深度不確定性進(jìn)行實(shí)時體積 3D 重建的原因:使用全深度 BA 的成本高得令人望而卻步,而使用稀疏深度 BA 會導(dǎo)致深度圖過于稀疏,無法進(jìn)行體積重建重建。
替代方案一直是使用稀疏 BA 進(jìn)行姿態(tài)估計(jì)和幾何形狀的第一次猜測,然后是與稀疏 BA 中的信息矩陣無關(guān)的致密化步驟 [20]。
這就是為什么其他作者建議對密集 SLAM 使用替代 3D 表示,例如 CodeSLAM [3] 中的潛在向量。我們的方法也可以應(yīng)用于 CodeSLAM
3.2.逆深度不確定性估計(jì)
鑒于 Hessian 的稀疏模式,我們可以有效地提取每像素深度變量所需的邊際協(xié)方差。逆深度圖 Σd 的邊際協(xié)方差由下式給出: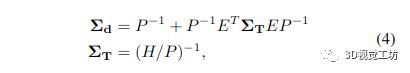
其中 ΣT 是姿態(tài)的邊際協(xié)方差。不幸的是,H/P 的完全反演計(jì)算成本很高。然而,由于我們已經(jīng)通過將 H/P 分解為其 Cholesky 因子來解決原始 BA 問題,我們可以通過以下方式重新使用它們,類似于 [8]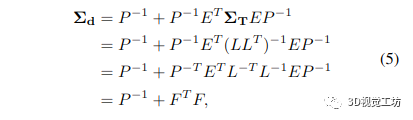
其中 F=L-1EP-1。因此,我們只需要反轉(zhuǎn)下三角 Cholesky 因子 L,這是一個通過代入計(jì)算的快速操作。因此,我們可以有效地計(jì)算所有逆矩陣:P 的逆由每個對角線元素的逐元素逆給出,我們通過取反它的 Cholesky 因子來避免 (H/P ) 的完全逆。然后將矩陣相乘和相加就足夠了: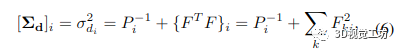
其中 di 是每個像素的逆深度之一。由于大多數(shù)操作都可以并行計(jì)算,因此我們利用了 GPU 的大規(guī)模并行性
3.3.深度上采樣和不確定性傳播
最后,由于我們想要一個與原始圖像分辨率相同的深度圖,我們使用 Raft [23] 中定義的凸上采樣運(yùn)算符對低分辨率深度圖進(jìn)行上采樣,該運(yùn)算符也在 Droid [24] 中使用.這種上采樣操作通過采用低分辨率深度圖中相鄰深度值的凸組合來計(jì)算高分辨率深度圖中每個像素的深度估計(jì)。通過以下方式為每個像素給出生成的深度估計(jì):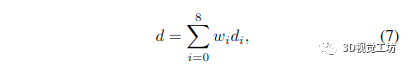
其中 wi 是學(xué)習(xí)的權(quán)重(更多細(xì)節(jié)可以在 Raft [23] 中找到),di 是我們正在計(jì)算深度的像素周圍的低分辨率逆深度圖中像素的逆深度(a 3 × 3 窗口用于采樣相鄰的深度值) 假設(shè)逆深度估計(jì)之間的獨(dú)立性,得到的逆深度方差由下式給出: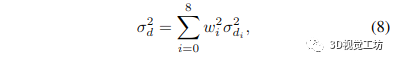
其中 wi 是用于方程式中的逆深度上采樣的相同權(quán)重。 (7)式,為待計(jì)算像素周圍低分辨率逆深度圖中某個像素的逆深度方差。我們將逆深度和不確定性上采樣 8 倍,從 69 × 44 分辨率到 512 × 384 分辨率。 到目前為止,我們一直在處理反深度,最后一步是將它們轉(zhuǎn)換為實(shí)際深度和深度方差。我們可以使用非線性不確定性傳播輕松計(jì)算深度方差: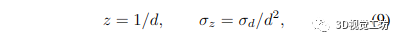
其中 z 是生成的深度,d 是反深度。
3.4.不確定性感知體積映射
鑒于每個關(guān)鍵幀可用的密集深度圖,可以構(gòu)建場景的密集 3D 網(wǎng)格。不幸的是,深度圖由于它們的密度而非常嘈雜,因?yàn)榧词故菬o紋理區(qū)域也會被賦予深度值。體積融合這些深度圖降低了噪聲,但重建仍然不準(zhǔn)確并且被偽影破壞(參見圖 4 中的“基線”,它是通過融合圖 1 中所示的點(diǎn)云計(jì)算的) 雖然可以在深度圖上手動設(shè)置過濾器(有關(guān)可能的深度過濾器示例,請參閱 PCL 的文檔 [19])并且 Droid 實(shí)現(xiàn)了一個 ad-hoc 深度過濾器(參見圖 4 中的 Droid),但我們建議改用估計(jì)的深度圖的不確定性,這提供了一種穩(wěn)健且數(shù)學(xué)上合理的方式來重建場景。
體積融合基于概率模型[7],其中假設(shè)每個深度測量是獨(dú)立的和高斯分布的。在這個公式下,我們嘗試估計(jì)的帶符號距離函數(shù) (SDF) φ 最大化了以下可能性: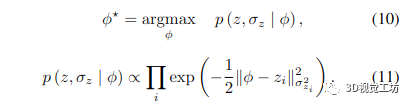
取負(fù)對數(shù)會導(dǎo)致加權(quán)最小二乘問題: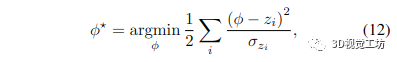
其解決方案是通過將梯度設(shè)置為零并求解 φ 獲得的,從而導(dǎo)致所有深度測量的加權(quán)平均值:
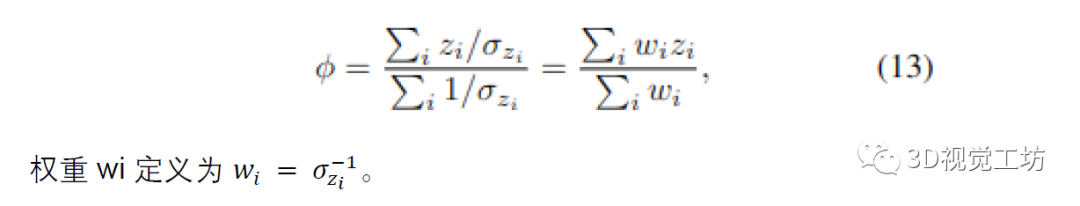
在實(shí)踐中,通過使用運(yùn)行平均值更新體積中的體素,為每個新的深度圖增量計(jì)算加權(quán)平均值,從而得出熟悉的體積重建方程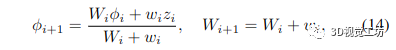
其中 Wi 是存儲在每個體素中的權(quán)重。權(quán)重初始化為零,W0 = 0,TSDF 初始化為截?cái)嗑嚯x τ,φ0 = τ(在我們的實(shí)驗(yàn)中,τ = 0.1m)。
上面的公式作為移動加權(quán)平均值,在使用的權(quán)重函數(shù)方面非常靈活。這種靈活性導(dǎo)致了融合深度圖的許多不同方法,有時會偏離其概率公式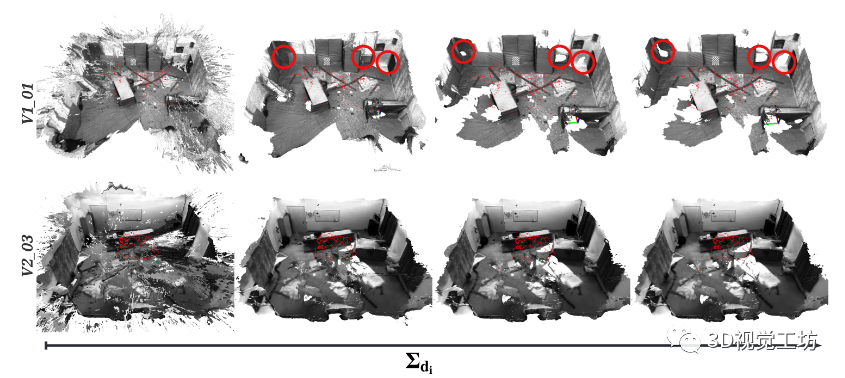
圖 2. 給定最大允許網(wǎng)格不確定性 Σdi 的 3D 網(wǎng)格重建從無窮大上限(即最小權(quán)重 0.0,最左側(cè)的 3D 網(wǎng)格)到 0.01(即最小權(quán)重 10,最右側(cè)的 3D 網(wǎng)格)呈對數(shù)下降.由于高度不確定性,用紅色圓圈突出顯示的區(qū)域首先消失。這些對應(yīng)于無紋理和混疊區(qū)域。兩個最接近的紅色圓圈對應(yīng)于與圖 3 中描繪的區(qū)域相同的區(qū)域。
大多數(shù)方法通過對所用深度傳感器的誤差分布進(jìn)行建模來確定權(quán)重函數(shù),無論是激光掃描儀、RGB-D 相機(jī)還是立體相機(jī) [7、15、18]。例如,Nguyen 等人。 [14] 對來自 RGB-D 相機(jī)的殘差進(jìn)行建模,并確定深度方差由 z2 主導(dǎo),z 是測量的深度。拜洛等人。 [5] 分析了各種權(quán)重函數(shù),并得出結(jié)論,在表面后面線性遞減的權(quán)重函數(shù)會導(dǎo)致最佳結(jié)果。
Voxblox [15] 將這兩個工作組合成一個簡化的公式,效果很好,它也被用于 Kimera [17] 在我們的例子中,不需要復(fù)雜的加權(quán)或傳感器模型;深度不確定性是根據(jù) SLAM 中固有的概率因子圖公式計(jì)算的。具體來說,我們的權(quán)重與深度的邊際協(xié)方差成反比,這是從方程式中的概率角度得出的。 (13).值得注意的是,這些權(quán)重來自數(shù)百個光流測量與神經(jīng)網(wǎng)絡(luò)估計(jì)的相關(guān)測量噪聲的融合(GRU 在 Droid [24] 中的輸出)。
3.5.不確定性界限的網(wǎng)格劃分
鑒于我們的體素對帶符號的距離函數(shù)具有概率合理的不確定性估計(jì),我們可以提取不同級別的等值面以允許最大不確定性。我們使用行進(jìn)立方體提取表面,只對那些不確定性估計(jì)低于最大允許不確定性的體素進(jìn)行網(wǎng)格劃分。生成的網(wǎng)格只有具有給定上限不確定性的幾何體,而我們的體積包含所有深度圖的信息 如果我們將不確定性邊界設(shè)置為無窮大,即權(quán)重為 0,我們將恢復(fù)基線解決方案,該解決方案非常嘈雜。
通過逐漸減小邊界,我們可以在更準(zhǔn)確但更不完整的 3D 網(wǎng)格之間取得平衡,反之亦然。
在第 4 節(jié)中,我們展示了隨著不確定性界限值的降低而獲得的不同網(wǎng)格(圖 2)。在我們的實(shí)驗(yàn)中,我們沒有嘗試為我們的方法找到特定的帕累托最優(yōu)解,而是使用不確定性 0.1 的固定最大上限,這導(dǎo)致非常準(zhǔn)確的 3D 網(wǎng)格,完整性略有損失(參見第 4 節(jié)進(jìn)行定量評估)。請注意,在不固定比例的情況下,此不確定性界限是無單位的,可能需要根據(jù)估計(jì)的比例進(jìn)行調(diào)整
3.6.實(shí)現(xiàn)細(xì)節(jié)
我們使用 CUDA 在 Pytorch 中執(zhí)行所有計(jì)算,并使用 RTX 2080 Ti GPU 進(jìn)行所有實(shí)驗(yàn)(11Gb 內(nèi)存)。對于體積融合,我們使用 Open3D 的 [30] 庫,它允許自定義體積集成。我們使用相同的GPU 用于 SLAM 并執(zhí)行體積重建。我們使用來自 Droid-SLAM [24] 的預(yù)訓(xùn)練權(quán)重。最后,我們使用 Open3D 中實(shí)現(xiàn)的行進(jìn)立方體算法來提取 3D 網(wǎng)格。
4. 結(jié)果
第 4.2 節(jié)和第 4.3 節(jié)展示了我們提出的 3D 網(wǎng)格重建算法的定性和定量評估,相對于基線和最先進(jìn)的方法,在 EuRoC 數(shù)據(jù)集上,使用具有以下場景的子集真實(shí)點(diǎn)云 定性分析展示了我們方法的優(yōu)缺點(diǎn),并在感知質(zhì)量和幾何保真度方面與其他技術(shù)進(jìn)行了比較。
對于定量部分,我們計(jì)算了準(zhǔn)確性和完整性指標(biāo)的 RMSE,以客觀地評估性能我們的算法對競爭方法的影響。我們現(xiàn)在描述數(shù)據(jù)集和用于評估的不同方法
4.1.數(shù)據(jù)集和評估方法
為了評估我們的重建算法,我們使用了 EuRoC 數(shù)據(jù)集,該數(shù)據(jù)集由在室內(nèi)空間飛行的無人機(jī)記錄的圖像組成。我們使用 EuRoC V1 和 V2 數(shù)據(jù)集中可用的地面實(shí)況點(diǎn)云來評估我們的方法生成的 3D 網(wǎng)格的質(zhì)量。對于我們所有的實(shí)驗(yàn),我們將最大允許網(wǎng)格不確定性設(shè)置為 0.1 我們將我們的方法與兩種不同的開源最先進(jìn)的學(xué)習(xí)和基于模型的密集 VO 算法進(jìn)行比較:Tandem [10],一種學(xué)習(xí)的密集單目 VO 算法,它使用 MVSNet 風(fēng)格的架構(gòu)和光度學(xué)捆綁包 -調(diào)整和 Kimera [17],一種基于模型的密集立體 VIO 算法。
兩者都使用體積融合來重建 3D 場景并輸出環(huán)境的 3D 網(wǎng)格。我們還展示了在 Droid 的 ad-hoc 深度過濾器之后融合 Droid 的點(diǎn)云的結(jié)果,該過濾器通過計(jì)算在閾值(默認(rèn)為 0.005)內(nèi)重新投影的附近深度圖的數(shù)量來計(jì)算深度值的支持。然后丟棄任何小于 2 個支持深度或小于平均深度一半的深度值。
Droid 的過濾器用于去除深度圖上的異常值,而我們?nèi)诤纤杏刹淮_定性加權(quán)的深度圖。作為我們的基線,我們使用 Droid 估計(jì)的原始點(diǎn)云,并將它們直接融合到體積重建中
4.2.定性建圖性能
圖2顯示了我們?nèi)绾瓮ㄟ^改變3D重建中允許的最大不確定性水平來權(quán)衡精確度的完整性。我們還可以看到不太確定的幾何形狀是如何逐漸消失的。最不確定的幾何形狀對應(yīng)于漂浮在3D空間中的偽影,因?yàn)樯疃热腔缓茫?dāng)反向投影時散落在3D射線中(圖2中的第一列)。
然后,我們看到消失的后續(xù)幾何形狀對應(yīng)于無紋理區(qū)域(每列中最左邊和最右邊的紅色圓圈)。有趣的是,在無紋理區(qū)域之后移除的幾何形狀對應(yīng)于高度鋸齒的區(qū)域(圖2中每列中的中間紅色圓圈),例如加熱器或房間中棋盤格的中心。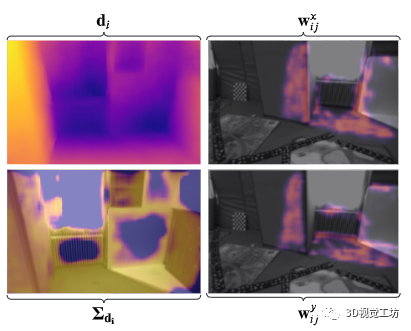
圖 3.(左列)第 i 幀。 (右欄)第 j 幀。 (左上)第 i 幀的估計(jì)深度圖。 (左下)幀 i 的估計(jì)深度圖不確定性。 (右上)從第 i 幀到第 j 幀的光流 x 分量的光流測量權(quán)重。 (右下)y 分量的光流測量權(quán)重。請注意,流權(quán)重位于幀 i 在幀 j 中可見的位置。深度的不確定性來自多個光流測量的融合,而不是單個光流測量。
對于左列,低值顯示為黃色,高值顯示為藍(lán)色。對于右列,低值顯示為藍(lán)色,高值顯示為黃色。 EuRoC V1 01 數(shù)據(jù)集 仔細(xì)觀察圖 3 可以看出,估計(jì)的深度不確定性 Σd 不僅對于無紋理區(qū)域很大,而且對于具有強(qiáng)混疊的區(qū)域也很難解決基于光流的 SLAM 算法(中間的加熱器)圖片)。實(shí)際上,對于具有強(qiáng)混疊或無紋理區(qū)域的區(qū)域,光流權(quán)重(圖 3 中的右欄)接近于 0。
這種新出現(xiàn)的行為是一個有趣的結(jié)果,可用于檢測混疊幾何,或指導(dǎo)孔填充重建方法。
圖 4. Kimera [17]、Tandem [10]、我們的基線和 Droid 的深度過濾器 [24](使用默認(rèn)閾值 0.005)重建的 3D 網(wǎng)格與我們使用最大容忍網(wǎng)格不確定性 0.1 的方法的比較。 EuRoC V2 01 數(shù)據(jù)集 圖4定性地比較了Kimera[17]、Tan晚會[10]、基線方法、Droid[24]和我們的方法的3D重建。
我們可以看到,與我們的基線方法相比,我們在準(zhǔn)確性和完整性方面都表現(xiàn)得更好。Kimera能夠構(gòu)建完整的3D重建,但與我們的方法相比,缺乏準(zhǔn)確性和細(xì)節(jié)。Tandem是表現(xiàn)最好的競爭方案,并且比我們提議的方法產(chǎn)生了相似的重建結(jié)果。
從圖4中,我們可以看到Tandem比我們的更完整(見我們重建中右下角缺失的地板條),同時稍微不太準(zhǔn)確(見重建的左上角部分,在Tandem的網(wǎng)格中扭曲)。原則上,我們的方法也可以重建房間的底層(基線重建有這些信息)。
盡管如此,在機(jī)器人環(huán)境中,最好是意識到哪個區(qū)域是未知的,而不是做出不準(zhǔn)確的第一次猜測,因?yàn)檫@可能會關(guān)閉機(jī)器人可能穿過的路徑(DARPA SubT挑戰(zhàn)賽[1]中的一個常見場景,機(jī)器人探索隧道和洞穴網(wǎng)絡(luò))。最后,Droid的深度過濾器缺少重要區(qū)域,并對重建精度產(chǎn)生負(fù)面影響。
表 1. 精度 RMSE [m]:對于我們的方法生成的 3D 網(wǎng)格,與 Kimera、Tandem、Droid 的過濾器和我們的基線相比,在具有地面實(shí)況點(diǎn)云的 EuRoC 數(shù)據(jù)集的子集上。請注意,如果一種方法僅估計(jì)幾個準(zhǔn)確的點(diǎn)(例如 Droid),則準(zhǔn)確度可以達(dá)到 0。粗體為最佳方法,斜體為次優(yōu),- 表示未重建網(wǎng)格。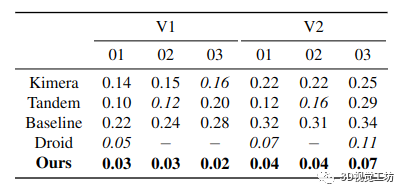
表 2. 完整性 RMSE [m]:對于我們的方法生成的 3D 網(wǎng)格,與 Kimera、Tandem 和我們的基線相比,在具有地面實(shí)況點(diǎn)云的 EuRoC 數(shù)據(jù)集的子集上。請注意,如果一種方法估計(jì)密集的點(diǎn)云(例如基線),則完整性可以達(dá)到 0。粗體為最佳方法,斜體為次優(yōu),- 表示未重建網(wǎng)格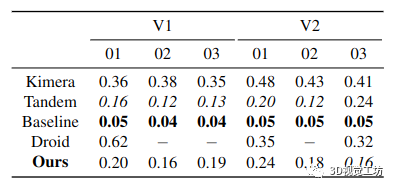
4.3.定量建圖性能
我們使用精度和完整性度量根據(jù)地面實(shí)況評估每個網(wǎng)格,如[16,第4.3節(jié)]:(i)我們首先通過以104點(diǎn)/m2的均勻密度對重建的3D網(wǎng)格進(jìn)行采樣來計(jì)算點(diǎn)云,(ii)我們使用CloudCompare[6]將估計(jì)的和地面實(shí)況云注冊到ICP[2],以及(iii)我們評估從地面實(shí)況點(diǎn)云到估計(jì)點(diǎn)云中最近鄰居的平均距離(精度),反之亦然(完整性),具有0.5m最大差異 第 4.2 節(jié)和第 4.3 節(jié)提供了我們提出的方法、Droid 的過濾器和我們的基線之間的定量比較,以及與 Kimera [17] 和 Tandem [10] 在準(zhǔn)確性和完整性方面的比較。
從表中可以看出,我們提出的方法在準(zhǔn)確性方面表現(xiàn)最好,差距很大(與 Tandem 相比高達(dá) 90%,與 V1 03 的基線相比高達(dá) 92%),而 Tandem 達(dá)到了第二 -整體最佳準(zhǔn)確度。在完整性方面,Tandem 實(shí)現(xiàn)了最佳性能(在基線方法之后),其次是我們的方法。 Droid 的過濾器以基本不完整的網(wǎng)格為代價實(shí)現(xiàn)了良好的精度。 圖 6 顯示了 Tandem(頂部)和我們的重建(底部)的估計(jì)云(V2 01)根據(jù)到地面真實(shí)云中最近點(diǎn)的距離(準(zhǔn)確性)進(jìn)行顏色編碼。我們可以從這個圖中看到我們的重建比 Tandem 的更準(zhǔn)確。
特別是有趣的是,Tandem 傾向于生成膨脹的幾何體,特別是在無紋理區(qū)域,例如 V2 01 數(shù)據(jù)集中的黑色窗簾(灰色幾何體)。我們的方法具有更好的細(xì)節(jié)和更好的整體準(zhǔn)確性。圖。圖 5 顯示了 Tandem 和我們的方法重建的 3D 網(wǎng)格的特寫視圖。我們的重建往往不太完整并且存在出血邊緣,但保留了大部分細(xì)節(jié),而 Tandem 的重建缺乏整體細(xì)節(jié)和傾向于略微膨脹,但保持更完整。
4.4.實(shí)時性能
將 Euroc 圖像下采樣到 512×384 分辨率導(dǎo)致每秒 15 幀的跟蹤速度。計(jì)算深度不確定性會使跟蹤速度降低幾幀/秒至 13 幀/秒。體積融合深度估計(jì),有或沒有深度不確定性,需要不到 20 毫秒。總的來說,我們的管道能夠以每秒 13 幀的速度實(shí)時重建場景,通過并行攝像機(jī)跟蹤和體積重建,并使用自定義 CUDA 內(nèi)核
圖 5. 仔細(xì)觀察 Tandem 的 3D 重建與我們的之間的差異。
EuRoC V2 01 數(shù)據(jù)集
圖 6. Tandem(上)和我們(下)的 3D 網(wǎng)格重建結(jié)果的精度評估。我們在 0.05m 處截?cái)嗌珮?biāo),并將其上方的任何內(nèi)容可視化為灰色,最多 0.5m(超出此誤差的幾何圖形將被丟棄)。請注意,我們的重建在 0.37m 處有最大誤差,而 Tandem 的最大誤差超出了 0.5m 的界限。
EuRoC V2 01 數(shù)據(jù)集。
5.結(jié)論
我們提出了一種使用密集的單目SLAM和快速深度不確定性計(jì)算和傳播的3D重建場景的方法。我們表明,我們的深度圖不確定性是準(zhǔn)確和完整的3D體積重建的可靠信息來源,從而產(chǎn)生具有顯著降低噪聲和偽影的網(wǎng)格。
鑒于我們的方法提供的映射精度和概率不確定性估計(jì),我們可以預(yù)見未來的研究將集中在地圖中不確定區(qū)域的主動探索上,通過結(jié)合語義學(xué)來重建其幾何形狀之外的3D場景,如Kimera語義[18],或者通過使用神經(jīng)體積隱式響應(yīng)進(jìn)行光度精確的3D重建,如Nice-SLAM。
審核編輯:劉清
-
RGB
+關(guān)注
關(guān)注
4文章
804瀏覽量
59680 -
SLAM
+關(guān)注
關(guān)注
24文章
436瀏覽量
32373 -
過濾器
+關(guān)注
關(guān)注
1文章
436瀏覽量
20277 -
計(jì)算機(jī)視覺
+關(guān)注
關(guān)注
9文章
1706瀏覽量
46612
原文標(biāo)題:密集單目 SLAM 的概率體積融合
文章出處:【微信號:3D視覺工坊,微信公眾號:3D視覺工坊】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
從基本原理到應(yīng)用的SLAM技術(shù)深度解析
SLAM技術(shù)的應(yīng)用及發(fā)展現(xiàn)狀
單目視覺SLAM仿真系統(tǒng)的設(shè)計(jì)與實(shí)現(xiàn)
高仙SLAM具體的技術(shù)是什么?SLAM2.0有哪些優(yōu)勢?
激光SLAM和視覺SLAM各擅勝場,融合使用、取長補(bǔ)短潛力巨大
視覺SLAM技術(shù)淺談
視覺SLAM深度解讀
基于概率運(yùn)動統(tǒng)計(jì)特征匹配的單目視覺SLAM算法
多無人機(jī)局部地圖數(shù)據(jù)共享融合的SLAM方法
輻射場的實(shí)時密集單眼SLAM簡析
單目立體視覺:我用單目相機(jī)求了個體積!
機(jī)器人移動過程中基于概率模型的SLAM方法

MG-SLAM:融合結(jié)構(gòu)化線特征優(yōu)化高斯SLAM算法

【AIBOX 應(yīng)用案例】單目深度估計(jì)

一種基于點(diǎn)、線和消失點(diǎn)特征的單目SLAM系統(tǒng)設(shè)計(jì)






 密集單目SLAM的概率體積融合概述
密集單目SLAM的概率體積融合概述










評論