所有DAC都表現出一定程度的諧波失真,這是當DAC的輸入由代表理想均勻采樣正弦波的數字序列驅動時,DAC在其輸出端再現完美正弦波的程度的指標。由于DAC的非理想瞬態和靜態行為,輸出頻譜將包含諧波成分。DAC的瞬態輸出特性包括壓擺率限制、不對稱上升和下降時間以及有限的建立時間。靜態特性與傳遞函數如何偏離直線有關。本文重點介紹靜態行為,并定義了一種從輸出頻譜中觀察到的諧波成分推導出DAC傳遞函數的方法。該分析假設傳遞函數而不是瞬態輸出特性是觀察到的諧波失真的主要來源。這個假設在低頻時是有效的。
DAC傳遞函數
圖1顯示了一個理想的DAC傳遞函數,即對角直線y=mx+b。數字輸入位于 x 軸上,模擬輸出位于 y 軸上。
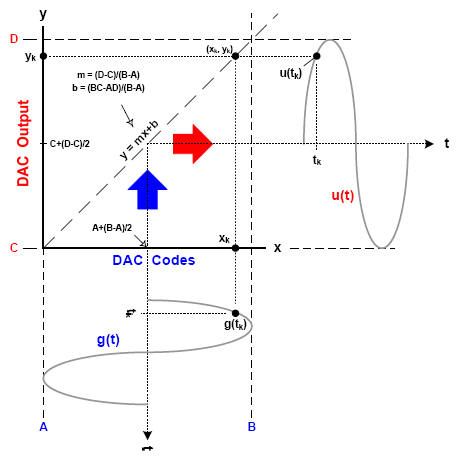
圖1.理想的DAC傳遞函數。
x 軸上的感興趣范圍是從左側的最小代碼 (A) 到右側的最大代碼 (B)。y 軸上感興趣的范圍是從底部的最低輸出值 (C) 到頂部 (D) 附近的最大輸出值。定義理想傳遞函數的斜率 (m) 和 y 截距 (b) 的方程以邊界值 A、B、C 和 D 表示。信號g(t)表示一個未失真的正弦波,由A和B范圍內的數字輸入組成,隨時間向下發展。信號u(t)代表模擬輸出,它跨越從C到D的值,時間向右發展。
輸出信號是通過傳遞函數對輸入信號的反射。請注意,輸出信號是將 g(t) 上的每個點鏈接到 u(t) 上的關聯點的結果。圖 1 顯示了特定時間時刻 t=t 的傳輸操作示例k,用于標識點 g(tk) 在輸入信號上。反過來,傳遞函數鏈接 g(tk) 到相應的點,u(tk),在輸出信號上。對于理想的線性傳遞函數,u(t) 將是 g(t) 的縮放版本。請注意,g(tk) 對應于點 xk在 X 軸上,通過傳遞函數反射到點 Yk在 y 軸上。耦合點集的先驗知識 (g(tn),u(tn)) 可以識別關聯的點 (xn,yn) 上的傳遞函數。因此,輸入信號上的點g(t)和輸出信號上的點u(t)之間的關系完全定義了傳遞函數。
對于N位DAC,邊界值A和B具有特定值;即,A = 0 和 B = 2N–1.另一方面,邊界值 C 和 D 可以方便地指定為 C = A 和 D = B。此分配意味著實際DAC輸出信號的比例和偏移,因此其峰峰值跨度為0至2N–1.使用這些 A、B、C 和 D 值,理想的傳遞函數簡化為 y = x,因為斜率和截距變為 m = 1 和 b = 0。
到目前為止,重點一直放在理想的DAC傳遞函數上,但我們現在有了處理失真的DAC傳遞函數f(x)的工具,如圖2所示。需要注意的主要特征是傳遞函數不再是直線 y = x,而是形狀函數 f(x),在這里任意顯示為平滑弧。同樣重要的是f(x)對輸出函數u(t)的影響。理想輸入 g(t) 反射傳遞函數 f(x),產生失真輸出 u(t)。與任何現成的DAC相比,所示的傳遞函數被高度夸大,顯示的戲劇性弧線僅用于說明目的。現代DAC的傳遞函數幾乎不會偏離理想的直線,但即使是最輕微的偏差也會導致輸出頻譜中出現諧波雜散。

圖2.失真的DAC傳遞函數。
DAC傳遞函數的成功重建依賴于確定每個點的能力,(xk,f(xk)),來自g(t)和u(t)的知識。這是一個兩步過程:首先使用代表完美采樣正弦波的數字序列驅動DAC輸入,使用頻譜分析儀測量DAC輸出,并記錄基波信號的幅度和盡可能多的諧波;然后將測得的諧波幅度轉換為具有特定形狀的傳遞函數。如果操作得當,通過將g(t)傳遞到f(x)來模擬u(t)將產生與測量值相同的諧波失真值。
第一步:測量DAC諧波
第一步需要一個輸入序列,該序列表示以均勻間隔的時間間隔采樣的完美正弦波的一個周期。目標是重建DAC傳遞函數,因此輸入信號必須至少包含從0到2的每個DAC代碼的出現一次N–1.輸入序列需要 2 個以上N使用等間距的樣本來執行每個DAC代碼,實際上至少需要2N+3示例,以保證命中每個代碼。以下公式產生 2 的完美正弦序列K帶有 K ≥ N+3 的 DAC 代碼。函數 round{x} 將 x 舍入到最接近的整數。

| 其中 n=0,1,2,3, ...2K–1 |
該公式假設DAC以直接二進制格式解碼數字輸入字,作為0到2的無符號整數N–1.對于失調二進制或二進制補碼DAC,gn必須進行調整以指示負值。
數字序列 (gn) 以采樣速率 f 重復輸送到 DACs,因此DAC輸出頻譜包含頻率f的基波信號0=fs/2K.諧波出現在2f處0, 3F0, 4F0和 f 的其他整數倍0.由于DAC輸出頻譜的采樣性質,這些諧波的幅度受sin(x)/x響應的影響。因為 f0是 f 的一小部分s但是,sin(x)/x 響應幾乎是平坦的,可以忽略。例如,對于 8 位 DAC,K ≥ 11 和 f0≤ fs/2048,因此 sin(x)/x 將不超過 0.39% (0.034 dB) 輸出到 100千諧波。
精確重建傳遞函數f(x)需要根據一組諧波數(h)記錄盡可能多的諧波幅度。這些整數以h = 1(基頻)開始,以h=H結束,其中H是測量幅度的最高諧波數。例如,對于測量值 10千諧波,H = 10,諧波數的集合是 h={1, 2, 3, .. 10}。
接下來,將每個測量諧波的幅度(M)與其諧波數相關聯。例如,M1是 1 的量級圣諧波(基波),M2是 2 的量級德·諧波,依此類推通過 MH.諧波幅度通常以相對于基波幅度(dBc)的分貝為單位。通過以下方式將 dBc 轉換為線性單位:

其中 D 是以 dBc 為單位的測量諧波幅度。例如,如果 3 的大小RD諧波為 –40 dBc,則線性幅度為 M3= 10–40/20,或 0.01。M1始終等于 1,因為根據定義,基波的大小為 0 dBc。
第二步:重建DAC傳遞函數
該過程的第二步涉及將測量的諧波與傳遞函數相關聯。f(x) 上的點取決于 g(t) 和 u(t) 上相應點之間的關系,因此頻域中的諧波幅度必須首先轉換為時域表示。請注意,g(t) 由 DAC 代碼組成,這些代碼與與 g(t) 的正弦形式相關的時間點具有一對一的對應關系。因此,包含g(t)的DAC碼與時域有關。此外,由于u(t)通過f(x)與g(t)相關,并且g(t)是一個時域函數,因此u(t)也必須表示為時域函數。這允許每個時間點,tk,在 g(t) 中鏈接到其在 u(t) 中的關聯時間點,這對于從 g(t) 和 u(t) 確定 f(x) 是必要的。
將諧波幅度轉換為時域表示具有挑戰性,因為f(x)必須與每個可能的DAC碼(0到2N–1) 以 g(t) 為單位。由于g(t)是一個完美的正弦曲線,確保唯一性的唯一方法是將范圍限制在正弦波單調遞增的地方,如圖3突出顯示的部分所示。如果沒有這樣的限制,f(x) 上的單個點可以映射到 g(t) 上的兩個點并導致歧義。
為了證明這種模糊性,想象一下向下滑動區域T。點 (xk, f(xk)) 在 f(x) 上現在可以與 g(t) 上的兩個點相關聯,這是不可接受的。通過將 T 的范圍限制為所示的范圍,歧義就不存在。由于g(t)是正弦曲線,因此所需的T范圍對應于初始相位偏移為3π/2弧度的<>/<>周期。

圖3.f(x) 和 g(t) 之間的關系。
g(t) 以 T 為界的事實意味著在 u(t) 上也有類似的界限。因此,將記錄的諧波幅度轉換為時域必須確保將u(t)限制在與g(t)相同的T范圍內,如圖4所示。

圖4.g(t) 和 u(t) 的時域范圍。
請注意,實際時間跨度 T 無關緊要,因為 f(x) 僅用于在 g(t) 和 u(t) 的振幅之間進行轉換。為了簡化分析,請歸一化基頻 (f0) 到 1。頻率 2德·因此諧波為2,頻率為3RD諧波為 3,依此類推。因此,諧波頻率與諧波數(h)相同:fh=h.這種方便的關系簡化了用于從諧波測量創建u(t)的數學,Mh.
正弦波的一般時域表示為:
 |
其中β是峰值振幅;θ 為初始相位偏移 |
每個諧波的時域表示,uh(t),可以通過用h代替f和M來實現h為β。但是,回想一下,g(t) 偏移了 3π/2 弧度。此外,g(t) 和 u(t) 之間通過 f(x) 的鏈接意味著 g(t) 和 u(t) 在相位上對齊。用 3π/2 代替 θ 可提供所需的對齊方式。在下面的等式中,請注意 0 ≤ t < 1,π 替換 2π 以將基波限制為半周期,如區間 T 所示:

了解每個諧波的時域表示后,uh(t),可以重建復合輸出u(t),作為基波和諧波信號的總和:

回想一下,目標是通過關聯g(t)和u(t)來重建DAC傳遞函數f(x)。此外,g(t) 必須正好由 2N樣本,以便與 f(x) 上的點保持一對一的對應關系。因此,將 g(t) 的樣本計算為:

| (n=0,1,2,3 .. 2N–1) |
由于 g(t) 由 2 組成N樣本,從由 2 個樣本集組成的 U(T) 樣本集中重建 f(x) 似乎是合理的N樣品。然而,事實證明,至少有 2N+3需要樣品才能為小值 M 提供合適的精度h.考慮到這一點,按如下方式計算 u(t) 的每個樣本:
 |
(n=0,1,2,3 .. 2N+3–1) |
請注意,這會導致 u(t) 包含比 g(t) 更多的樣本。這使得 u(t) 和 g(t) 到 f(x) 的映射變得復雜,因為 u(t) 的多個樣本可以對應于 f(x) 和 g(t) 上的單個點。因此,必須對特定的樣本組進行平均,以便提供對f(x)的合理映射。以下偽代碼演示了假設 N 位 DAC 所需的映射,2Ng(t) 和 2 的點N+3你的點(t)。陣列 DacXfr 由 2 個N元素,最初為零。執行代碼后,DacXfr 數組的元素包含規范化的 DAC 傳遞函數。
n = 0
FOR i = 0 TO 2N–1
AvgCnt = 0
WHILE i = g[n]
AvgCnt = AvgCnt + 1
DacXfr[i] = DacXfr[i] + u[n]
n = n + 1
IF n >= 2N+3
EXIT WHILE
END IF
END WHILE
IF AvgCnt = 0
EXIT (fail because array, g[ ], is missing a DAC code)
END IF
DacXfr[i] = (DacXfr[i]/AvgCnt)/2N
END FOR
驗證
為了驗證本文中描述的方法,使用頻譜分析儀測量由代表完美正弦波的輸入序列驅動的14位DAC的輸出。記錄前2次諧波的幅度(數字15至1,單位為dBc),并使用這些值重建DAC傳遞函數f(x)。接下來,仿真通過重構的DAC傳遞函數f(x)傳遞理想的正弦輸入序列g(t)來生成輸出序列u(t)。FFT 將 u(t) 轉換為其頻域等效項 U(ω)。從U(ω)中提取諧波幅度,并與頻譜分析儀測量值進行比較,如表7的表格結果所示。請注意,最大的誤差,與 <>千諧波,僅為0.065分貝。
表1
| 諧波數 | 測量幅度 (dBc) | 模擬幅度(分貝) | 偏差(分貝) |
| 1 | 0.00 | 0.00 | 0.000 |
| 2 | -75.1 | -75.100 | 0.000 |
| 3 | -74.5 | -74.502 | -0.002 |
| 4 | -90.5 | -90.501 | -0.001 |
| 5 | -86.5 | -86.498 | 0.002 |
| 6 | -92.0 | -91.999 | 0.001 |
| 7 | -95.5 | -95.565 | -0.065 |
| 8 | -93.8 | -93.801 | -0.001 |
| 9 | -97.2 | -97.187 | 0.013 |
| 10 | -89.6 | -89.599 | 0.001 |
| 11 | -94.2 | -94.204 | -0.004 |
| 12 | -98.8 | -98.802 | -0.002 |
| 13 | -95.6 | -95.649 | -0.049 |
| 14 | -99.3 | -99.298 | 0.002 |
| 15 | -91.1 | -91.080 | 0.020 |
由于比例,重建傳遞函數的圖顯示為直線 (y = x)。事實上,傳遞函數實際上偏離y = x足以產生表1所示的諧波成分。它有助于僅繪制傳遞函數與理想直線的偏差,如圖 5 所示。縱軸以 LSB 為單位。

圖5.DAC傳遞函數的殘余誤差。
審核編輯:郭婷
-
dac
+關注
關注
43文章
2381瀏覽量
193105 -
函數
+關注
關注
3文章
4372瀏覽量
64291
發布評論請先 登錄
開環傳遞函數是怎樣影響系統的?
LCL濾波器傳遞函數和逆變器諧波的理解
由DAC諧波頻譜成分重構其傳遞函數

DAC傳遞函數資料下載

傳遞函數極點和零點的影響是什么
傳遞函數的頻率特性
各轉換器的傳遞函數-升降壓轉換器的傳遞函數導出示例 其1





 根據其諧波頻譜內容重構DAC傳遞函數
根據其諧波頻譜內容重構DAC傳遞函數










評論