一、引言
以下我們引用文獻【1】中的一段話作為本文的開始:
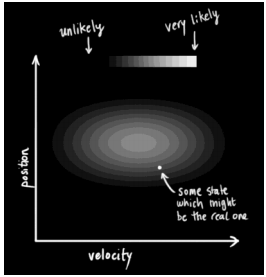
想象你在黃昏時分看著一僅僅小鳥飛行穿過濃密的叢林。你僅僅能隱隱約約、斷斷續(xù)續(xù)地瞥見小鳥運動的閃現(xiàn)。你試圖努力地猜測小鳥在哪里以及下一時刻它會出如今哪里,才不至于失去它的行蹤。或者再想象你是二戰(zhàn)中的一名雷達操作員,正在跟蹤一個微弱的游移目標。這個目標每隔10秒鐘在屏幕上閃爍一次。
或者回到更遠的從前。想象你是開普勒,正試圖依據一組通過不規(guī)則和不準確的測量間隔得到的非常不精確的角度觀測值來又一次構造行星的運動軌跡。在全部這些情況下。你都試圖依據隨對問變化并且?guī)в性肼暤挠^察數據去預計物理系統(tǒng)的狀態(tài)(比如位置、速度等等)。這個問題能夠被形式化表示為時序概率模型上的推理,模型中的轉移模型描寫敘述了運動的物理本質,而傳感器模型則描寫敘述了測量過程。
為解決這類問題。人們發(fā)展出來了一種特殊的表示方法和推理算法——卡爾曼濾波。
二、基本概念
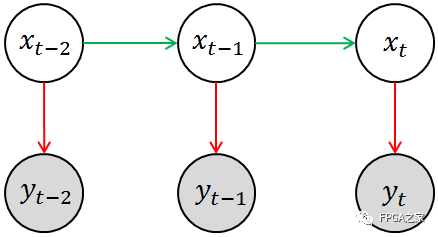
回憶一下HMM的基本模型(例如以下圖所看到的)。當中涂有陰影的圓圈(yt-2,yt-1,yt)相當于是觀測變量,空白圓圈(xt-2,xt-1,xt)相當于是隱變量。
這事實上揭示了卡爾曼濾波與HMM之間擁有非常深的淵源。
回到剛剛提及的那幾個樣例,你所觀測到的物體狀態(tài)(比如雷達中目標的位置或者速度)相當于是對其真實狀態(tài)的一種預計(由于觀測的過程中必定存在噪聲),用數學語言來表述就是P(yt|xt),這就是模型中的測量模型或測量概率(Measurement Probability)。另外一方面,物體當前的(真實)狀態(tài)應該與其上一個觀測狀態(tài)相關,即存在這樣的一個分布P(xt|xt-1),這就是模型中的轉移模型或轉移概率(Transition Probability)。當然,HMM中隱變量必須都是離散的,觀測變量并無特殊要求。
而從信號處理的角度來講,濾波是從混合在一起的諸多信號中提取出所需信號的過程[2]。比如,我們有一組含有噪聲的行星執(zhí)行軌跡。我們希望濾除當中的噪聲,預計行星的真實運動軌跡。這一過程就是濾波。
假設從機器學習和數據挖掘的角度來說。濾波是一個理性智能體為了把握當前狀態(tài)以便進行理性決策所採取的行動[1]。比方,前兩天我們沒出門,可是我們能夠從房間里觀察路上的行人有沒有打傘(觀測狀態(tài))來預計前兩天有沒有下雨(真實狀態(tài))。
基于這些情況,如今我們要來決策今天(是否會有雨以及)外出是否須要打傘。這個過程就是濾波。
讀者應該注意把握上面兩個定義的統(tǒng)一性。
所謂預計就是依據測量得出的與狀態(tài)X(t) 有關的數據Y(t) =h[X(t)] + V(t) 解算出X(t)的計算值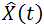 ,當中隨機向量V(t) 為測量誤差,
,當中隨機向量V(t) 為測量誤差,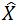 稱為X的預計,Y 稱為 X 的測量。
稱為X的預計,Y 稱為 X 的測量。
由于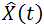 是依據Y(t) 確定的.所以
是依據Y(t) 確定的.所以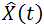 ?是Y(t) 的函數。
?是Y(t) 的函數。
若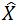 ?是Y 的線性函數。則 X?稱作 X 的線性預計。設在 [t0,?t1] 時間段內的測量為Y。對應的預計為
?是Y 的線性函數。則 X?稱作 X 的線性預計。設在 [t0,?t1] 時間段內的測量為Y。對應的預計為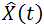 。則
。則
當t=t1時。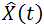 ?稱為X(t)的預計。
?稱為X(t)的預計。
當t>t1肘,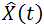 稱為X(t)的預測;
稱為X(t)的預測;
當t稱為X(t)的平滑。
最優(yōu)預計是指某一指標函數達到最值時的預計。
卡爾曼濾波就是一種線性最優(yōu)濾波器。
由于后面會用到。這里我們補充一下關于協(xié)方差矩陣的概念。
設n維隨機變量(X1,X2,…,Xn)的2階混合中心距
σij= cov(Xi,Xj) = E[(Xi-E(Xi))(Xj-E(Xj))], (i,j = 1, 2,…,n)
都存在,則稱矩陣
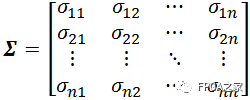
為n維隨機變量(X1,X2,…,Xn)的協(xié)方差矩陣,協(xié)方差矩陣是一個對稱矩陣,并且對角線是各個維度的方差。
維基百科中還給出了協(xié)方差矩陣的一些重要性質,比如以下這兩條(此處不做具體證明)。
興許的內容會用到當中的第一條。
三、卡爾曼濾波的方程推導
直接從數學公式和概念入手來考慮卡爾曼濾波無疑是一件非常枯燥的事情。為了便于理解,我們仍然從一個現(xiàn)實中的實例開始以下的介紹。這一過程中你所需的預備知識僅僅是高中程度的物理學內容。
假如如今有一輛在路上做直線運動的小車(例如以下所看到的),該小車在t時刻的狀態(tài)能夠用一個向量來表示,當中pt表示他當前的位置,vt表示該車當前的速度。當然,司機還能夠踩油門或者剎車來給車一個加速度ut。ut相當于是一個對車的控制量。顯然,假設司機既沒有踩油門也沒有踩剎車,那么ut就等于0。此時車就會做勻速直線運動。

假設我們已知上一時刻t-1時小車的狀態(tài)。如今來考慮當前時刻t小車的狀態(tài)。顯然有
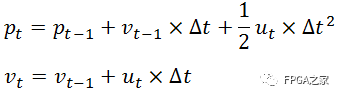
易知。上述兩個公式中,輸出變量都是輸入變量的線性組合,這也就是稱卡爾曼濾波器為線性濾波器的原因所在。既然上述公式表征了一種線性關系。那么我們就能夠用一個矩陣來表示它,則有
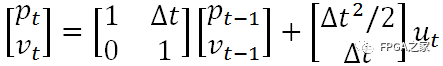
假設另當中的

則得到卡爾曼濾波方程組中的第一條公式——狀態(tài)預測公式,而F就是狀態(tài)轉移矩陣。它表示我們怎樣從上一狀態(tài)來猜測當前狀態(tài)。而B則是控制矩陣,它表示控制量u怎樣作用于當前狀態(tài)。
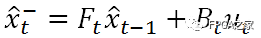 ???(1)
???(1)
上式中x頂上的hat表示為預計值(而非真實值)。等式左端部分的右上標“-”表示該狀態(tài)是依據上一狀態(tài)猜測而來的,稍后我們還將對其進行修正以得到最優(yōu)預計。彼時才干夠將“-”去掉。
既然我們是在對真實值進行預計,那么就理應考慮到噪聲的影響。
實踐中,我們通常都是假設噪聲服從一個0均值的高斯分布。即Noise~Guassian(0,σ)。
比如對于一個一維的數據進行預計時,若要引入噪聲的影響。事實上僅僅要考慮當中的方差σ就可以。當我們將維度提高之后。為了綜合考慮各個維度偏離其均值的程度,就須要引入協(xié)方差矩陣。
回到我們的樣例。系統(tǒng)中每一個時刻的不確定性都是通過協(xié)方差矩陣Σ來給出的。
并且這樣的不確定性在每一個時刻間還會進行傳遞。也就是說不僅當前物體的狀態(tài)(比如位置或者速度)是會(在每一個時刻間)進行傳遞的,并且物體狀態(tài)的不確定性也是會(在每一個時刻間)進行傳遞的。這樣的不確定性的傳遞就能夠用狀態(tài)轉移矩陣來表示,即(注意。這里用到了前面給出的關于協(xié)方差矩陣的性質)
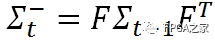
可是我們還應該考慮到。預測模型本身也并不絕對準確的,所以我們要引入一個協(xié)方差矩陣Q來表示預測模型本身的噪聲(也即是噪聲在傳遞過程中的不確定性),則有
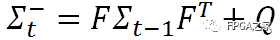 ? (2)
? (2)
這就是卡爾曼濾波方程組中的第二條公式,它表示不確定性在各個時刻間的傳遞關系。
繼續(xù)我們的小汽車樣例。你應該注意到,前面我們所討論的內容都是環(huán)繞小汽車的真實狀態(tài)展開的。
而真實狀態(tài)我們事實上是無法得知的,我們僅僅能通過觀測值來對真實值進行預計。
所以如今我們在路上布設了一個裝置來測定小汽車的位置。觀測到的值記為Y(t)。
并且從小汽車的真實狀態(tài)到其觀測狀態(tài)另一個變換關系。這個變換關系我們記為h(?)。并且這個h(?)還是一個線性函數。此時便有(該式前面以前給出過)
Y(t) =h[X(t)] + V(t)
當中V(t)表示觀測的誤差。既然h(?)還是一個線性函數,所以我們相同能夠把上式改寫成矩陣的形式。則有
Yt=Hxt+ v
就本例而言,觀測矩陣H= [1 0],這事實上告訴我們x和Z的維度不一定非得相同。
在我們的樣例中,x是一個二維的列向量,而Z僅僅是一個標量。此時當把x與上面給出的H相乘就會得出一個標量,此時得到的Y就是x中的首個元素,也就是小車的位置。
相同,我們還須要用一個協(xié)方差矩陣R來代替上述式子中的v來表示觀測中的不確定性。
當然,由于Z是一個一維的值,所以此時協(xié)方差矩陣R也僅僅有一維,也就是僅僅有一個值,即觀測噪聲之高斯分布的參數σ。假設我們有非常多裝置來測量小汽車的不同狀態(tài),那么Z就會是一個包括全部觀測值的向量。
接下來要做的事情就是對前面得出的狀態(tài)預計進行修正,具體而言就是利用以下這個式子
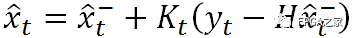 ??? (4)
??? (4)
直觀上來說,上式并不難理解。前面我們提到。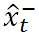 是依據上一狀態(tài)猜測而來的。那么它與“最優(yōu)”預計值之間的差距如今就是等式右端加號右側的部分。
是依據上一狀態(tài)猜測而來的。那么它與“最優(yōu)”預計值之間的差距如今就是等式右端加號右側的部分。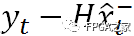 表示實際觀察值與預估的觀測值之間的殘差。這個殘差再乘以一個系數K就能夠用來對預計值進行修正。
表示實際觀察值與預估的觀測值之間的殘差。這個殘差再乘以一個系數K就能夠用來對預計值進行修正。
K稱為卡爾曼系數,它也是一個矩陣,它是對殘差的加權矩陣。有的資料上稱其為濾波增益陣。
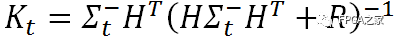 ?? (3)
?? (3)
上式的推導比較復雜,有興趣深入研究的讀者能夠參閱文獻【2】(P35~P37)。
假設有時間我會在后面再做具體推導。可是如今我們仍然能夠定性地對這個系數進行解讀:濾波增益陣首先權衡預測狀態(tài)協(xié)方差矩陣Σ和觀測值矩陣R的大小。并以此來認為我們是更傾向于相信預測模型還是具體觀測模型。
假設相信預測模型多一點。那么這個殘差的權重就會小一點。反之亦然。假設相信觀察模型多一點,這個殘差的權重就會大一點。不僅如此,濾波增益陣還負責把殘差的表現(xiàn)形式從觀測域轉換到了狀態(tài)域。
比如本題中觀測值Z僅僅是一個一維的向量,狀態(tài)x是一個二維的向量。
所以在實際應用中,觀測值與狀態(tài)值所採用的描寫敘述特征或者單位都有可能不同,顯然直接用觀測值的殘差去更新狀態(tài)值是不合理的。
而利用卡爾曼系數,我們就能夠完畢這樣的轉換。比如。在小車運動這個樣例中,我們僅僅觀察到了汽車的位置,但K里面已經包括了協(xié)方差矩陣P的信息(P里面就給出了速度和位置的相關性)。所以它利用速度和位置這兩個維度的相關性,從位置的殘差中推算出了速度的殘差。
從而讓我們能夠對狀態(tài)值x的兩個維度同一時候進行修正。
最后,還需對最優(yōu)預計值的噪聲分布進行更新。所使用的公式為
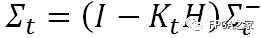 ?(5)
?(5)
至此。我們便獲得了實現(xiàn)卡爾曼濾波所需的全部五個公式,我在前面分別用(1)~(5)的標記進行了編號。我如今把它們再次羅列出來:

我們將這五個公式分成預測組和更新組。
預測組總是依據前一個狀態(tài)來預計當前狀態(tài)。更新組則依據觀測信息來對預測信息進行修正。以期達到最優(yōu)預計之目的。
四、一個簡單的實例
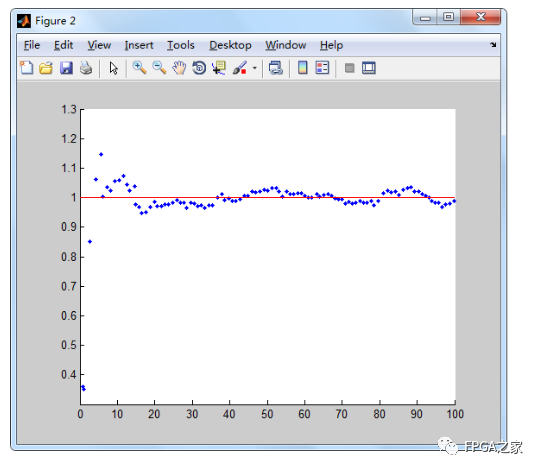
當然,你可能困惑于卡爾曼濾波是否真的有效。以下利用文獻[4]中給出的樣例(為提升顯示效果。筆者略有改動)來演示卡爾曼濾波的威力。
這個樣例模擬質點進行勻速直線運動(速度為1),然后引入一個非常大的噪聲。再用卡爾曼濾波來對質點的運動狀態(tài)進行軌跡。注意是勻速直線運動。所以當中不含有控制變量。
Z=(1:100); %觀測值
noise=randn(1,100); %方差為1的高斯噪聲
Z=Z+noise;
X=[0; 0]; %狀態(tài)
Sigma = [1 0; 0 1]; %狀態(tài)協(xié)方差矩陣
F=[1 1; 0 1]; %狀態(tài)轉移矩陣
Q=[0.0001, 0; 0 0.0001]; %狀態(tài)轉移協(xié)方差矩陣
H=[1 0]; %觀測矩陣
R=1; %觀測噪聲方差
figure;
hold on;
for i=1:100
X_ = F*X;
Sigma_ = F*Sigma*F'+Q;
K = Sigma_*H'/(H*Sigma_*H'+R);
X = X_+K*(Z(i)-H*X_);
Sigma = (eye(2)-K*H)*Sigma_;
plot(X(1), X(2), '.','MarkerSize',10); %畫點,橫軸表示位置。縱軸表示速度
end
plot([0,100],[1,1],'r-');
下圖給出了上述代碼的執(zhí)行結果。
可見經過最開始的幾次迭代后。質點運動的狀態(tài)預計就回到了正確軌跡上,并且預計的結果基本環(huán)繞在真實值附近,效果還是非常理想的。
審核編輯:湯梓紅
-
傳感器
+關注
關注
2567文章
53145瀏覽量
768868 -
濾波器
+關注
關注
162文章
8154瀏覽量
182350 -
HMM
+關注
關注
0文章
14瀏覽量
10205 -
卡爾曼濾波
+關注
關注
3文章
166瀏覽量
25116 -
機器學習
+關注
關注
66文章
8510瀏覽量
134841
原文標題:仔細看完你就懂卡爾曼濾波(Kalman Filter)
文章出處:【微信號:zhuyandz,微信公眾號:FPGA之家】歡迎添加關注!文章轉載請注明出處。
發(fā)布評論請先 登錄
卡爾曼濾波的原理說明
卡爾曼濾波程序的轉換問題
卡爾曼濾波有哪些應用
卡爾曼濾波簡介
Kalman濾波在視頻監(jiān)控中的應用
什么是卡爾曼濾波? 淺談卡爾曼濾波眼里的機器人問題
卡爾曼濾波的變種有哪些?1
卡爾曼濾波的變種有哪些?2





 仔細看完你就懂卡爾曼濾波(Kalman Filter)
仔細看完你就懂卡爾曼濾波(Kalman Filter)

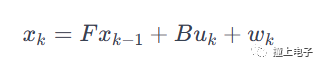
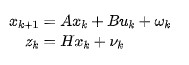











評論