01前言伯克利的馬毅教授在線上開(kāi)展了為期 2 周的暑期課程,課程主講 3D視覺(jué),課程涉及內(nèi)容十分豐富,受限于版權(quán)原因可能不會(huì)公開(kāi),所有內(nèi)容都可以在馬老師的?An invitation to 3D vision?一書(shū)中進(jìn)行深入了解。本篇博客重點(diǎn)解讀 Two View Geometry 的部分內(nèi)容,這也是馬老師重點(diǎn)強(qiáng)調(diào)的內(nèi)容。其實(shí)這部分內(nèi)容在大多數(shù)課程和教材中都有涉及,很多人可能也覺(jué)得很簡(jiǎn)單,有一定的套路可言,但是如標(biāo)題所說(shuō),你真的理解Two View Geometry嗎?筆者曾面試過(guò) DJI 以及 Nreal 兩家很棒的公司,面試時(shí)都問(wèn)到了這一部分,當(dāng)時(shí)還覺(jué)得自己答得不錯(cuò),但是聽(tīng)過(guò)馬老師的課程之后發(fā)現(xiàn),其實(shí)我也并不是很了解 Two View Geometry。接下來(lái)我會(huì)依據(jù)馬老師的課件以及教材詳細(xì)介紹 Two View Geometry, 在這之后的下一篇博客我會(huì)介紹一篇 CVPR 2021 的工作 Deep Two-View Structure-from-Motion Revisited,下面進(jìn)入正式內(nèi)容。02Traditional Two View Geometry下面這張圖是一個(gè) Geometric Vision 的簡(jiǎn)略回顧: 大致歷程是:從雙視圖,到三視圖四視圖,再到統(tǒng)一的多視圖。內(nèi)容我們只涉及雙視圖的,按照書(shū)中的標(biāo)題來(lái)說(shuō)就是:Reconstruction from Two Calibrated Views. 所要做的事情就是,給定兩張同一場(chǎng)景不同視角下拍攝到的圖像,恢復(fù)出相機(jī)的位姿以及場(chǎng)景的結(jié)構(gòu)。
大致歷程是:從雙視圖,到三視圖四視圖,再到統(tǒng)一的多視圖。內(nèi)容我們只涉及雙視圖的,按照書(shū)中的標(biāo)題來(lái)說(shuō)就是:Reconstruction from Two Calibrated Views. 所要做的事情就是,給定兩張同一場(chǎng)景不同視角下拍攝到的圖像,恢復(fù)出相機(jī)的位姿以及場(chǎng)景的結(jié)構(gòu)。 我們假設(shè)先前的預(yù)備工作已經(jīng)準(zhǔn)備充分,相機(jī)已經(jīng)標(biāo)定完成,correspondence 也已經(jīng)匹配完成,那么不失一般性的可以用下面這個(gè)等式來(lái)進(jìn)行表述:
我們假設(shè)先前的預(yù)備工作已經(jīng)準(zhǔn)備充分,相機(jī)已經(jīng)標(biāo)定完成,correspondence 也已經(jīng)匹配完成,那么不失一般性的可以用下面這個(gè)等式來(lái)進(jìn)行表述: 這里
這里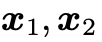 分別表示視角1以及視角2下,對(duì)空間中同一個(gè)點(diǎn)的觀測(cè),這里是使用歸一化平面坐標(biāo)進(jìn)行表達(dá),
分別表示視角1以及視角2下,對(duì)空間中同一個(gè)點(diǎn)的觀測(cè),這里是使用歸一化平面坐標(biāo)進(jìn)行表達(dá),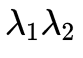 表示
表示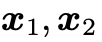 對(duì)應(yīng)的深度值,
對(duì)應(yīng)的深度值,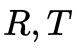 表示從視角 1 到視角 2 的 Rigid Body Motion。所謂恢復(fù) motion 以及 structure 就是計(jì)算深度
表示從視角 1 到視角 2 的 Rigid Body Motion。所謂恢復(fù) motion 以及 structure 就是計(jì)算深度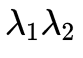 以及變換
以及變換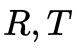 。(1)式在有多次觀測(cè)時(shí),
。(1)式在有多次觀測(cè)時(shí),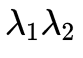 是一直變化的,而相機(jī)運(yùn)動(dòng)
是一直變化的,而相機(jī)運(yùn)動(dòng)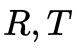 卻是始終不變的,為了追求統(tǒng)一,雖然說(shuō)法有些哲學(xué)(玄學(xué)),但是道理就是這么個(gè)道理,我們需要同時(shí)叉乘T,消去場(chǎng)景結(jié)構(gòu)帶來(lái)的影響,然后就得到了著名的Epipolar Geometry:
卻是始終不變的,為了追求統(tǒng)一,雖然說(shuō)法有些哲學(xué)(玄學(xué)),但是道理就是這么個(gè)道理,我們需要同時(shí)叉乘T,消去場(chǎng)景結(jié)構(gòu)帶來(lái)的影響,然后就得到了著名的Epipolar Geometry: 我們把
我們把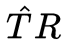 這個(gè)矩陣用
這個(gè)矩陣用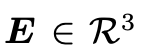 表示,并稱之為Essential matrix. 這是Longuet-Higgins 在 1981 年發(fā)現(xiàn)的,感謝前人貢獻(xiàn)。正如推導(dǎo)過(guò)程所闡述的,(2)式只與相機(jī)的運(yùn)動(dòng)有關(guān), right?并且因?yàn)?2)式右邊為0,說(shuō)明這是一個(gè)齊次等式,乘以任意的常數(shù)依然正確,而
表示,并稱之為Essential matrix. 這是Longuet-Higgins 在 1981 年發(fā)現(xiàn)的,感謝前人貢獻(xiàn)。正如推導(dǎo)過(guò)程所闡述的,(2)式只與相機(jī)的運(yùn)動(dòng)有關(guān), right?并且因?yàn)?2)式右邊為0,說(shuō)明這是一個(gè)齊次等式,乘以任意的常數(shù)依然正確,而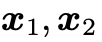 是觀測(cè),
是觀測(cè),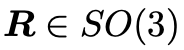 ,因此常數(shù)只能給
,因此常數(shù)只能給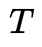 ,這也符合我們的常識(shí),即單目相機(jī)沒(méi)有辦法恢復(fù)尺度。但是沒(méi)有關(guān)系,we only care about the direction!對(duì)極幾何還表達(dá)了一個(gè)重要的屬性就是3點(diǎn)共面,
,這也符合我們的常識(shí),即單目相機(jī)沒(méi)有辦法恢復(fù)尺度。但是沒(méi)有關(guān)系,we only care about the direction!對(duì)極幾何還表達(dá)了一個(gè)重要的屬性就是3點(diǎn)共面,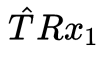 表示了這個(gè)平面的法向量,right?所以在什么情況下,法向量與
表示了這個(gè)平面的法向量,right?所以在什么情況下,法向量與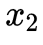 點(diǎn)乘為0呢?只能是共面。可以看到,代數(shù)與幾何是統(tǒng)一的,你甚至可以直接根據(jù)幾何寫出(2)式。對(duì)極幾何的表達(dá)十分簡(jiǎn)潔,并且有許多有趣的性質(zhì):
點(diǎn)乘為0呢?只能是共面。可以看到,代數(shù)與幾何是統(tǒng)一的,你甚至可以直接根據(jù)幾何寫出(2)式。對(duì)極幾何的表達(dá)十分簡(jiǎn)潔,并且有許多有趣的性質(zhì):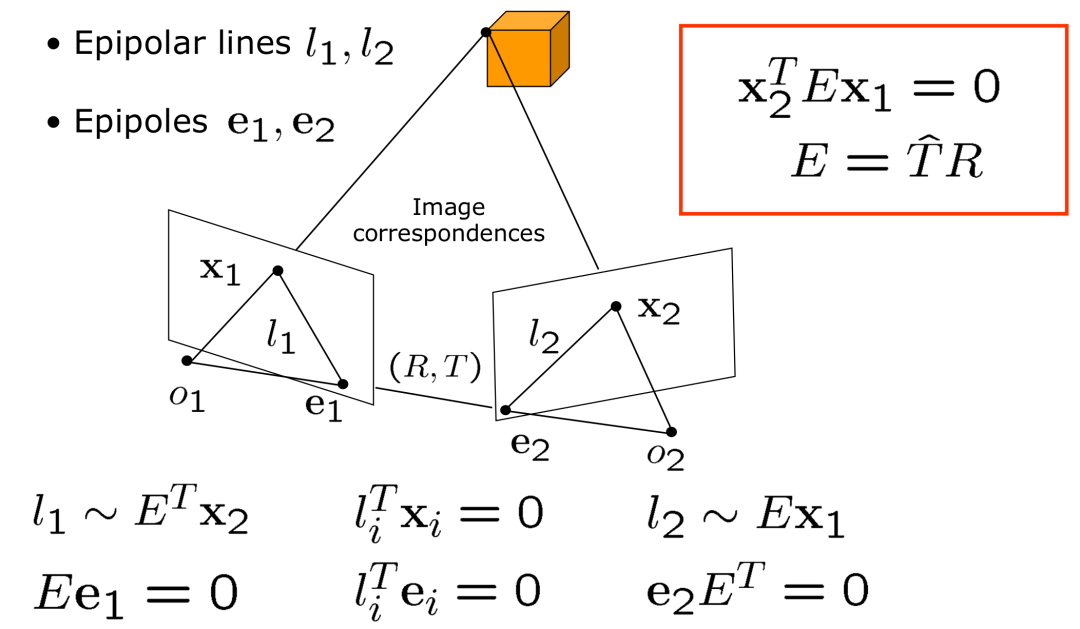 我們來(lái)稍加解讀。按照上面的說(shuō)法,對(duì)極幾何其實(shí)表達(dá)的是三點(diǎn)共面,
我們來(lái)稍加解讀。按照上面的說(shuō)法,對(duì)極幾何其實(shí)表達(dá)的是三點(diǎn)共面,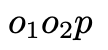 三個(gè)點(diǎn)會(huì)形成一個(gè)三角形,從而確定一個(gè)平面,不論空間點(diǎn)
三個(gè)點(diǎn)會(huì)形成一個(gè)三角形,從而確定一個(gè)平面,不論空間點(diǎn) 怎么變,
怎么變, 這條邊是不變的。在幾何層面,線和面不平行就會(huì)產(chǎn)生交點(diǎn),我們稱成像平面與
這條邊是不變的。在幾何層面,線和面不平行就會(huì)產(chǎn)生交點(diǎn),我們稱成像平面與 的交點(diǎn)為
的交點(diǎn)為 Epipoles:
Epipoles: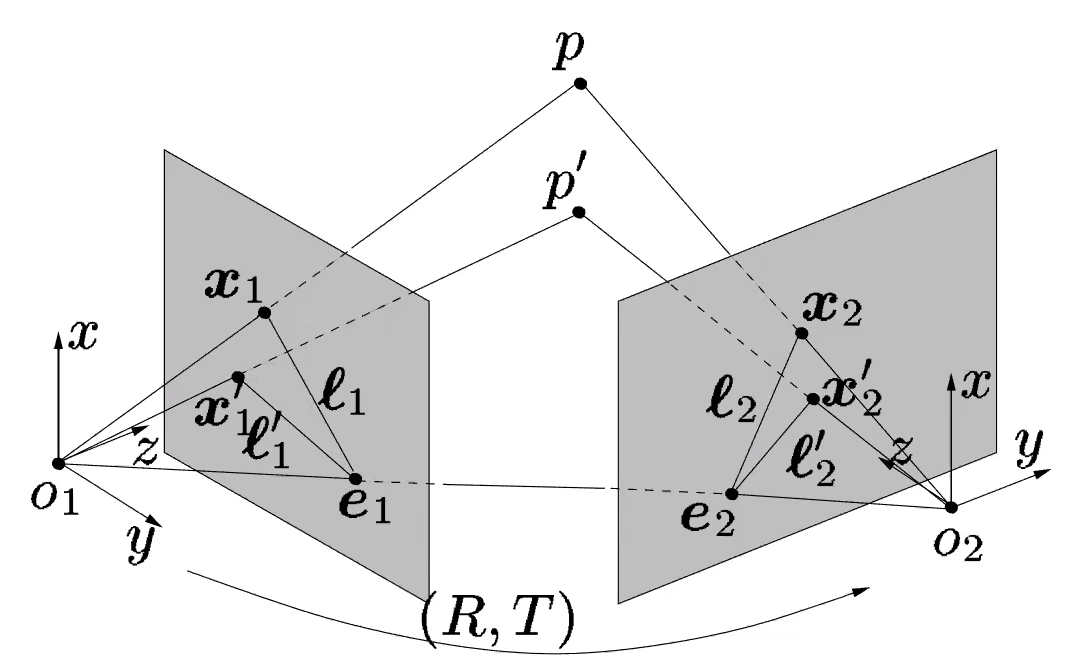 類似的你可以了解 Epipolar line 的定義。具體的性質(zhì)可以參考馬老師的書(shū),這里我簡(jiǎn)單描述一下,
類似的你可以了解 Epipolar line 的定義。具體的性質(zhì)可以參考馬老師的書(shū),這里我簡(jiǎn)單描述一下, 是極線,但是我們選擇用三角形平面的法向量去描述極線,因?yàn)榉ㄏ蛄看_定了極線就唯一確定了。剩下的挨個(gè)理一下就通了。接下來(lái)難度會(huì)提升一些。對(duì)極幾何很美,如何解呢?這個(gè)方程是 homo- geneous 的,因此E的自由度為最多為 8,事實(shí)上我們知道實(shí)際自由度是 5(旋轉(zhuǎn)矩陣的自由度為 3,不考慮尺度因素,平移向量的自由度為 2),但是暫且不考慮這個(gè)。因此如果給定8對(duì) correspondence(這里我們不考慮共線共面以及其他的corner case),至少E可以解出。接下來(lái)會(huì)面對(duì)兩個(gè)問(wèn)題:1.
是極線,但是我們選擇用三角形平面的法向量去描述極線,因?yàn)榉ㄏ蛄看_定了極線就唯一確定了。剩下的挨個(gè)理一下就通了。接下來(lái)難度會(huì)提升一些。對(duì)極幾何很美,如何解呢?這個(gè)方程是 homo- geneous 的,因此E的自由度為最多為 8,事實(shí)上我們知道實(shí)際自由度是 5(旋轉(zhuǎn)矩陣的自由度為 3,不考慮尺度因素,平移向量的自由度為 2),但是暫且不考慮這個(gè)。因此如果給定8對(duì) correspondence(這里我們不考慮共線共面以及其他的corner case),至少E可以解出。接下來(lái)會(huì)面對(duì)兩個(gè)問(wèn)題:1.  怎么解呢?2.假設(shè)你知道怎么解出
怎么解呢?2.假設(shè)你知道怎么解出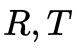 ,而實(shí)際應(yīng)用中,我們的correspondence都是很noise的,這樣得到的解也是帶噪聲的,那么如何把噪聲去掉,得到一個(gè)干干凈凈的Essential Matrix呢?帶著這些問(wèn)題繼續(xù)往下走。我們通過(guò)8個(gè)點(diǎn)對(duì),解出的矩陣記作
,而實(shí)際應(yīng)用中,我們的correspondence都是很noise的,這樣得到的解也是帶噪聲的,那么如何把噪聲去掉,得到一個(gè)干干凈凈的Essential Matrix呢?帶著這些問(wèn)題繼續(xù)往下走。我們通過(guò)8個(gè)點(diǎn)對(duì),解出的矩陣記作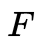 ,首先有一點(diǎn)你要了解,不是任何3×3的矩陣都能分解為
,首先有一點(diǎn)你要了解,不是任何3×3的矩陣都能分解為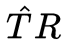 這種形式的,
這種形式的,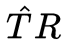 的自由度是6,如果upto scale的話,自由度則是5,并且包含一個(gè)
的自由度是6,如果upto scale的話,自由度則是5,并且包含一個(gè)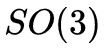 的旋轉(zhuǎn)矩陣部分,因此
的旋轉(zhuǎn)矩陣部分,因此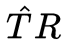 也是一個(gè) special group,有其對(duì)應(yīng)的空間(essential space),或者說(shuō) 5 維的流形上(essential manifold),當(dāng)有噪聲時(shí),得到的解
也是一個(gè) special group,有其對(duì)應(yīng)的空間(essential space),或者說(shuō) 5 維的流形上(essential manifold),當(dāng)有噪聲時(shí),得到的解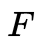 會(huì)在這個(gè)空間外。為了便于表達(dá),我們引入 normalized essential matrix 來(lái)消除尺度的干擾:
會(huì)在這個(gè)空間外。為了便于表達(dá),我們引入 normalized essential matrix 來(lái)消除尺度的干擾: 在后文我們提到的
在后文我們提到的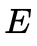 不特殊說(shuō)明都指的是normalized essential matrix.我們希望能在 essential space 中找到一個(gè)距離F最“近”的解,然后將F投影到這個(gè)解上,如下圖所示:
不特殊說(shuō)明都指的是normalized essential matrix.我們希望能在 essential space 中找到一個(gè)距離F最“近”的解,然后將F投影到這個(gè)解上,如下圖所示: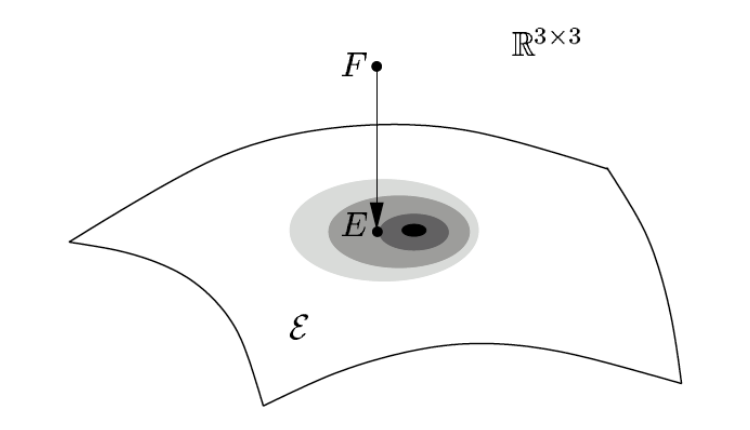 在說(shuō)明怎樣投影前,我們需要先給出三個(gè)定理:
在說(shuō)明怎樣投影前,我們需要先給出三個(gè)定理: 定理一描述了一個(gè)矩陣為 Essential Matrix 的充要條件。
定理一描述了一個(gè)矩陣為 Essential Matrix 的充要條件。 定理二描述了如何從 Essential Matrix 恢復(fù)到旋轉(zhuǎn)矩陣以及平移方向向量。這里需要注意的是,normalized essential matrix 可以消除尺度的干擾,但是不能消除符號(hào)的干擾,代數(shù)角度而言,E 和?E 都滿足Epipolar Constraint,因此實(shí)際我們能得到四組解。
定理二描述了如何從 Essential Matrix 恢復(fù)到旋轉(zhuǎn)矩陣以及平移方向向量。這里需要注意的是,normalized essential matrix 可以消除尺度的干擾,但是不能消除符號(hào)的干擾,代數(shù)角度而言,E 和?E 都滿足Epipolar Constraint,因此實(shí)際我們能得到四組解。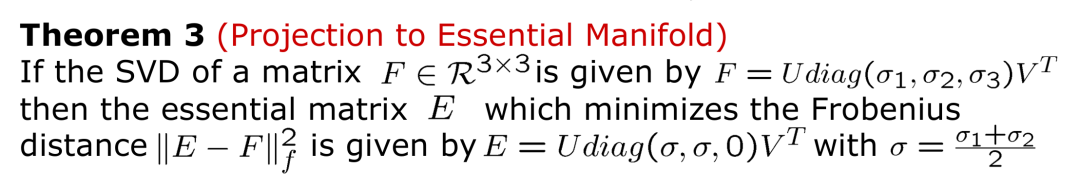 定理三給出了投影的方法,我們選擇F-norm作為投影距離的度量指標(biāo)。這里需要注意的是,
定理三給出了投影的方法,我們選擇F-norm作為投影距離的度量指標(biāo)。這里需要注意的是,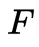 的SVD分解得到的
的SVD分解得到的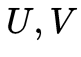 只滿足正交性,不能滿足行列式為+1的條件,當(dāng)?shù)玫降?/span>
只滿足正交性,不能滿足行列式為+1的條件,當(dāng)?shù)玫降?/span>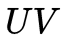 行列式為?1時(shí),我們會(huì)對(duì)其取負(fù),在后面我們會(huì)用代碼具體解釋。以上三個(gè)定理在馬老師的書(shū)里都有詳細(xì)證明,出于易讀性的考慮后續(xù)會(huì)單獨(dú)的整理到我的知乎上分享。在有了這三個(gè)定理之后,整個(gè)算法也就明朗了,流程如下:
行列式為?1時(shí),我們會(huì)對(duì)其取負(fù),在后面我們會(huì)用代碼具體解釋。以上三個(gè)定理在馬老師的書(shū)里都有詳細(xì)證明,出于易讀性的考慮后續(xù)會(huì)單獨(dú)的整理到我的知乎上分享。在有了這三個(gè)定理之后,整個(gè)算法也就明朗了,流程如下: 以上就是著名的八點(diǎn)法,你可以在許多資料上看到這個(gè)過(guò)程,本文的主要目的是梳理八點(diǎn)法的一些思路。我們引用一段 colmap 中的源碼來(lái)解讀上述過(guò)程:
以上就是著名的八點(diǎn)法,你可以在許多資料上看到這個(gè)過(guò)程,本文的主要目的是梳理八點(diǎn)法的一些思路。我們引用一段 colmap 中的源碼來(lái)解讀上述過(guò)程: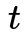 取
取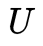 的最后一行可以留給讀者作為一個(gè)思考題,提示是
的最后一行可以留給讀者作為一個(gè)思考題,提示是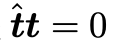 ,然后分析一下矩陣的秩。八點(diǎn)法十分簡(jiǎn)潔(當(dāng)然證明過(guò)程比較復(fù)雜),但是在實(shí)際使用過(guò)程中,還是會(huì)遇到許多問(wèn)題的,我們?cè)谝韵潞?jiǎn)要列舉:1. Number of points. 由于 Normalized Essential Matrix 的自由度為 5,在比較 general 的情況下,最少選取的 correspondence 點(diǎn)對(duì)為 5(Kruppa在 1913 年的時(shí)候給出了五點(diǎn)法,類似八點(diǎn)法會(huì)產(chǎn)生 4 個(gè)滿足對(duì)極約束的解,五點(diǎn)法會(huì)產(chǎn)生 10個(gè)解),因此選取多少點(diǎn)是一個(gè)需要實(shí)際使用中考慮的問(wèn)題。2. Number of solutions and positive depth constraint.雖然八點(diǎn)法給出了四對(duì)解,但是實(shí)際上只有一個(gè)正確解,那么其他三個(gè)解怎么排除呢?首先從代數(shù)層面,不要忘了最原始的表達(dá)式
,然后分析一下矩陣的秩。八點(diǎn)法十分簡(jiǎn)潔(當(dāng)然證明過(guò)程比較復(fù)雜),但是在實(shí)際使用過(guò)程中,還是會(huì)遇到許多問(wèn)題的,我們?cè)谝韵潞?jiǎn)要列舉:1. Number of points. 由于 Normalized Essential Matrix 的自由度為 5,在比較 general 的情況下,最少選取的 correspondence 點(diǎn)對(duì)為 5(Kruppa在 1913 年的時(shí)候給出了五點(diǎn)法,類似八點(diǎn)法會(huì)產(chǎn)生 4 個(gè)滿足對(duì)極約束的解,五點(diǎn)法會(huì)產(chǎn)生 10個(gè)解),因此選取多少點(diǎn)是一個(gè)需要實(shí)際使用中考慮的問(wèn)題。2. Number of solutions and positive depth constraint.雖然八點(diǎn)法給出了四對(duì)解,但是實(shí)際上只有一個(gè)正確解,那么其他三個(gè)解怎么排除呢?首先從代數(shù)層面,不要忘了最原始的表達(dá)式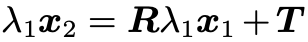 ,在這個(gè)表達(dá)式中隱藏了一個(gè)很關(guān)鍵的約束,深度值應(yīng)該為正,至于怎么求深度值是三角化部分的知識(shí)了,我們不在這里討論,如果你對(duì)上述過(guò)程熟悉,不難發(fā)現(xiàn)就是一個(gè)叉乘的技巧。基于這一約束我們可以將正確的解篩選出來(lái)。而從幾何層面來(lái)看,就是下面這張圖(From Multiple View Geometry in Computer Vision):
,在這個(gè)表達(dá)式中隱藏了一個(gè)很關(guān)鍵的約束,深度值應(yīng)該為正,至于怎么求深度值是三角化部分的知識(shí)了,我們不在這里討論,如果你對(duì)上述過(guò)程熟悉,不難發(fā)現(xiàn)就是一個(gè)叉乘的技巧。基于這一約束我們可以將正確的解篩選出來(lái)。而從幾何層面來(lái)看,就是下面這張圖(From Multiple View Geometry in Computer Vision):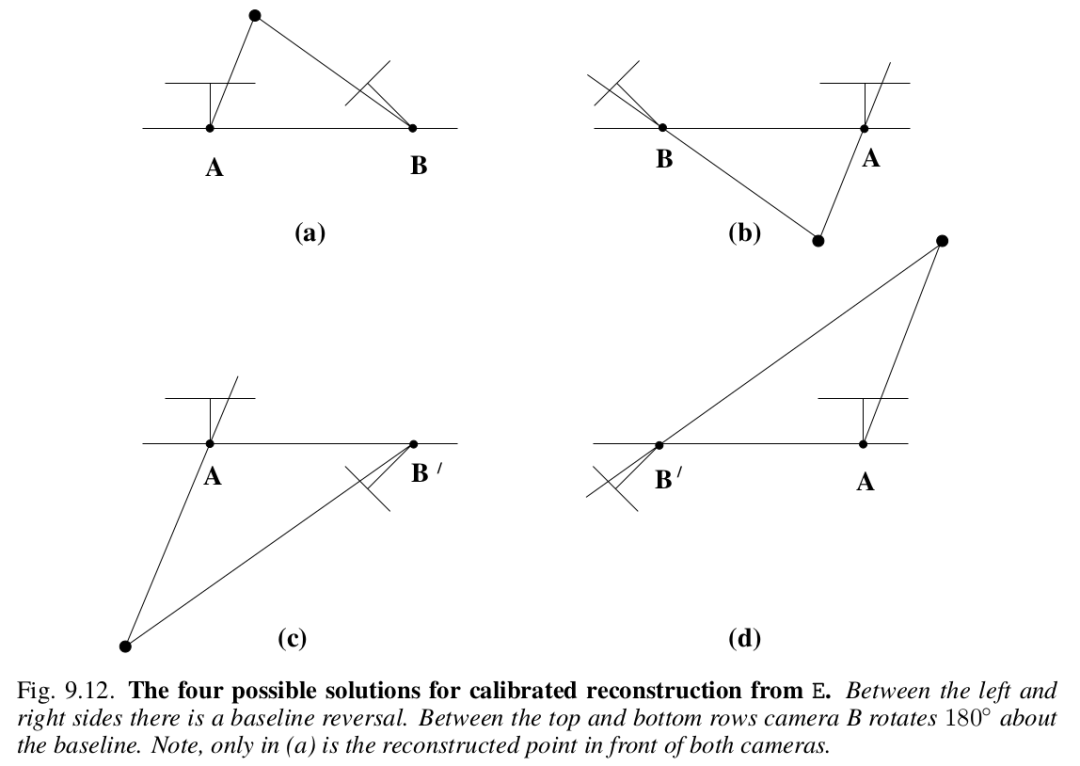 3. Structure requirement: general position.當(dāng)觀測(cè)到的空間點(diǎn)滿足某些導(dǎo)致退化的條件時(shí)(called critical surfaces),使用八點(diǎn)法會(huì)遇到解不唯一的情況。一個(gè)典型的例子就是觀測(cè)點(diǎn)共面的情況,這種時(shí)候我們需要使用homography 來(lái)解決。4. Motion requirement: su?icient parallax.也就是說(shuō),平移量不能為0(為0時(shí)也要使用 homography)。需要十分小心的是,在沒(méi)有平移移動(dòng)且匹配十分 noise 的時(shí)候,八點(diǎn)法依舊會(huì)得到一個(gè)很奇怪的平移部分的解,而這個(gè)解是毫無(wú)意義的。5. Multiple motion hypotheses.運(yùn)動(dòng)物體場(chǎng)景,這又是另一個(gè)問(wèn)題了。03結(jié)語(yǔ)Essential Matrix 之所以叫 Essential Matrix,就是因?yàn)樗匾? 馬老師花了4節(jié)課的時(shí)間,介紹two view geometry的內(nèi)容, 可見(jiàn)其重要性。目前學(xué)術(shù)的研究主要在于recognition的問(wèn)題了,也有許多工作還是聚焦在end to end的執(zhí)著,當(dāng)然這只是我個(gè)人的一些粗淺的看法。審核編輯 :李倩
3. Structure requirement: general position.當(dāng)觀測(cè)到的空間點(diǎn)滿足某些導(dǎo)致退化的條件時(shí)(called critical surfaces),使用八點(diǎn)法會(huì)遇到解不唯一的情況。一個(gè)典型的例子就是觀測(cè)點(diǎn)共面的情況,這種時(shí)候我們需要使用homography 來(lái)解決。4. Motion requirement: su?icient parallax.也就是說(shuō),平移量不能為0(為0時(shí)也要使用 homography)。需要十分小心的是,在沒(méi)有平移移動(dòng)且匹配十分 noise 的時(shí)候,八點(diǎn)法依舊會(huì)得到一個(gè)很奇怪的平移部分的解,而這個(gè)解是毫無(wú)意義的。5. Multiple motion hypotheses.運(yùn)動(dòng)物體場(chǎng)景,這又是另一個(gè)問(wèn)題了。03結(jié)語(yǔ)Essential Matrix 之所以叫 Essential Matrix,就是因?yàn)樗匾? 馬老師花了4節(jié)課的時(shí)間,介紹two view geometry的內(nèi)容, 可見(jiàn)其重要性。目前學(xué)術(shù)的研究主要在于recognition的問(wèn)題了,也有許多工作還是聚焦在end to end的執(zhí)著,當(dāng)然這只是我個(gè)人的一些粗淺的看法。審核編輯 :李倩
 大致歷程是:從雙視圖,到三視圖四視圖,再到統(tǒng)一的多視圖。內(nèi)容我們只涉及雙視圖的,按照書(shū)中的標(biāo)題來(lái)說(shuō)就是:Reconstruction from Two Calibrated Views. 所要做的事情就是,給定兩張同一場(chǎng)景不同視角下拍攝到的圖像,恢復(fù)出相機(jī)的位姿以及場(chǎng)景的結(jié)構(gòu)。
大致歷程是:從雙視圖,到三視圖四視圖,再到統(tǒng)一的多視圖。內(nèi)容我們只涉及雙視圖的,按照書(shū)中的標(biāo)題來(lái)說(shuō)就是:Reconstruction from Two Calibrated Views. 所要做的事情就是,給定兩張同一場(chǎng)景不同視角下拍攝到的圖像,恢復(fù)出相機(jī)的位姿以及場(chǎng)景的結(jié)構(gòu)。 我們假設(shè)先前的預(yù)備工作已經(jīng)準(zhǔn)備充分,相機(jī)已經(jīng)標(biāo)定完成,correspondence 也已經(jīng)匹配完成,那么不失一般性的可以用下面這個(gè)等式來(lái)進(jìn)行表述:
我們假設(shè)先前的預(yù)備工作已經(jīng)準(zhǔn)備充分,相機(jī)已經(jīng)標(biāo)定完成,correspondence 也已經(jīng)匹配完成,那么不失一般性的可以用下面這個(gè)等式來(lái)進(jìn)行表述: 這里
這里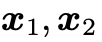 分別表示視角1以及視角2下,對(duì)空間中同一個(gè)點(diǎn)的觀測(cè),這里是使用歸一化平面坐標(biāo)進(jìn)行表達(dá),
分別表示視角1以及視角2下,對(duì)空間中同一個(gè)點(diǎn)的觀測(cè),這里是使用歸一化平面坐標(biāo)進(jìn)行表達(dá),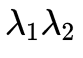 表示
表示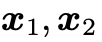 對(duì)應(yīng)的深度值,
對(duì)應(yīng)的深度值,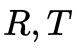 表示從視角 1 到視角 2 的 Rigid Body Motion。所謂恢復(fù) motion 以及 structure 就是計(jì)算深度
表示從視角 1 到視角 2 的 Rigid Body Motion。所謂恢復(fù) motion 以及 structure 就是計(jì)算深度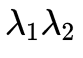 以及變換
以及變換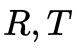 。(1)式在有多次觀測(cè)時(shí),
。(1)式在有多次觀測(cè)時(shí),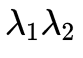 是一直變化的,而相機(jī)運(yùn)動(dòng)
是一直變化的,而相機(jī)運(yùn)動(dòng)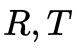 卻是始終不變的,為了追求統(tǒng)一,雖然說(shuō)法有些哲學(xué)(玄學(xué)),但是道理就是這么個(gè)道理,我們需要同時(shí)叉乘T,消去場(chǎng)景結(jié)構(gòu)帶來(lái)的影響,然后就得到了著名的Epipolar Geometry:
卻是始終不變的,為了追求統(tǒng)一,雖然說(shuō)法有些哲學(xué)(玄學(xué)),但是道理就是這么個(gè)道理,我們需要同時(shí)叉乘T,消去場(chǎng)景結(jié)構(gòu)帶來(lái)的影響,然后就得到了著名的Epipolar Geometry: 我們把
我們把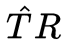 這個(gè)矩陣用
這個(gè)矩陣用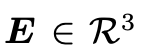 表示,并稱之為Essential matrix. 這是Longuet-Higgins 在 1981 年發(fā)現(xiàn)的,感謝前人貢獻(xiàn)。正如推導(dǎo)過(guò)程所闡述的,(2)式只與相機(jī)的運(yùn)動(dòng)有關(guān), right?并且因?yàn)?2)式右邊為0,說(shuō)明這是一個(gè)齊次等式,乘以任意的常數(shù)依然正確,而
表示,并稱之為Essential matrix. 這是Longuet-Higgins 在 1981 年發(fā)現(xiàn)的,感謝前人貢獻(xiàn)。正如推導(dǎo)過(guò)程所闡述的,(2)式只與相機(jī)的運(yùn)動(dòng)有關(guān), right?并且因?yàn)?2)式右邊為0,說(shuō)明這是一個(gè)齊次等式,乘以任意的常數(shù)依然正確,而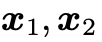 是觀測(cè),
是觀測(cè),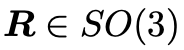 ,因此常數(shù)只能給
,因此常數(shù)只能給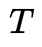 ,這也符合我們的常識(shí),即單目相機(jī)沒(méi)有辦法恢復(fù)尺度。但是沒(méi)有關(guān)系,we only care about the direction!對(duì)極幾何還表達(dá)了一個(gè)重要的屬性就是3點(diǎn)共面,
,這也符合我們的常識(shí),即單目相機(jī)沒(méi)有辦法恢復(fù)尺度。但是沒(méi)有關(guān)系,we only care about the direction!對(duì)極幾何還表達(dá)了一個(gè)重要的屬性就是3點(diǎn)共面,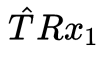 表示了這個(gè)平面的法向量,right?所以在什么情況下,法向量與
表示了這個(gè)平面的法向量,right?所以在什么情況下,法向量與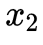 點(diǎn)乘為0呢?只能是共面。可以看到,代數(shù)與幾何是統(tǒng)一的,你甚至可以直接根據(jù)幾何寫出(2)式。對(duì)極幾何的表達(dá)十分簡(jiǎn)潔,并且有許多有趣的性質(zhì):
點(diǎn)乘為0呢?只能是共面。可以看到,代數(shù)與幾何是統(tǒng)一的,你甚至可以直接根據(jù)幾何寫出(2)式。對(duì)極幾何的表達(dá)十分簡(jiǎn)潔,并且有許多有趣的性質(zhì): 我們來(lái)稍加解讀。按照上面的說(shuō)法,對(duì)極幾何其實(shí)表達(dá)的是三點(diǎn)共面,
我們來(lái)稍加解讀。按照上面的說(shuō)法,對(duì)極幾何其實(shí)表達(dá)的是三點(diǎn)共面,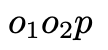 三個(gè)點(diǎn)會(huì)形成一個(gè)三角形,從而確定一個(gè)平面,不論空間點(diǎn)
三個(gè)點(diǎn)會(huì)形成一個(gè)三角形,從而確定一個(gè)平面,不論空間點(diǎn)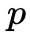 怎么變,
怎么變,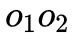 這條邊是不變的。在幾何層面,線和面不平行就會(huì)產(chǎn)生交點(diǎn),我們稱成像平面與
這條邊是不變的。在幾何層面,線和面不平行就會(huì)產(chǎn)生交點(diǎn),我們稱成像平面與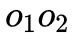 的交點(diǎn)為
的交點(diǎn)為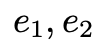 Epipoles:
Epipoles: 類似的你可以了解 Epipolar line 的定義。具體的性質(zhì)可以參考馬老師的書(shū),這里我簡(jiǎn)單描述一下,
類似的你可以了解 Epipolar line 的定義。具體的性質(zhì)可以參考馬老師的書(shū),這里我簡(jiǎn)單描述一下,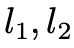 是極線,但是我們選擇用三角形平面的法向量去描述極線,因?yàn)榉ㄏ蛄看_定了極線就唯一確定了。剩下的挨個(gè)理一下就通了。接下來(lái)難度會(huì)提升一些。對(duì)極幾何很美,如何解呢?這個(gè)方程是 homo- geneous 的,因此E的自由度為最多為 8,事實(shí)上我們知道實(shí)際自由度是 5(旋轉(zhuǎn)矩陣的自由度為 3,不考慮尺度因素,平移向量的自由度為 2),但是暫且不考慮這個(gè)。因此如果給定8對(duì) correspondence(這里我們不考慮共線共面以及其他的corner case),至少E可以解出。接下來(lái)會(huì)面對(duì)兩個(gè)問(wèn)題:1.
是極線,但是我們選擇用三角形平面的法向量去描述極線,因?yàn)榉ㄏ蛄看_定了極線就唯一確定了。剩下的挨個(gè)理一下就通了。接下來(lái)難度會(huì)提升一些。對(duì)極幾何很美,如何解呢?這個(gè)方程是 homo- geneous 的,因此E的自由度為最多為 8,事實(shí)上我們知道實(shí)際自由度是 5(旋轉(zhuǎn)矩陣的自由度為 3,不考慮尺度因素,平移向量的自由度為 2),但是暫且不考慮這個(gè)。因此如果給定8對(duì) correspondence(這里我們不考慮共線共面以及其他的corner case),至少E可以解出。接下來(lái)會(huì)面對(duì)兩個(gè)問(wèn)題:1. 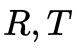 怎么解呢?2.假設(shè)你知道怎么解出
怎么解呢?2.假設(shè)你知道怎么解出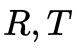 ,而實(shí)際應(yīng)用中,我們的correspondence都是很noise的,這樣得到的解也是帶噪聲的,那么如何把噪聲去掉,得到一個(gè)干干凈凈的Essential Matrix呢?帶著這些問(wèn)題繼續(xù)往下走。我們通過(guò)8個(gè)點(diǎn)對(duì),解出的矩陣記作
,而實(shí)際應(yīng)用中,我們的correspondence都是很noise的,這樣得到的解也是帶噪聲的,那么如何把噪聲去掉,得到一個(gè)干干凈凈的Essential Matrix呢?帶著這些問(wèn)題繼續(xù)往下走。我們通過(guò)8個(gè)點(diǎn)對(duì),解出的矩陣記作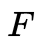 ,首先有一點(diǎn)你要了解,不是任何3×3的矩陣都能分解為
,首先有一點(diǎn)你要了解,不是任何3×3的矩陣都能分解為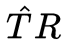 這種形式的,
這種形式的,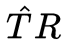 的自由度是6,如果upto scale的話,自由度則是5,并且包含一個(gè)
的自由度是6,如果upto scale的話,自由度則是5,并且包含一個(gè)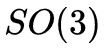 的旋轉(zhuǎn)矩陣部分,因此
的旋轉(zhuǎn)矩陣部分,因此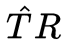 也是一個(gè) special group,有其對(duì)應(yīng)的空間(essential space),或者說(shuō) 5 維的流形上(essential manifold),當(dāng)有噪聲時(shí),得到的解
也是一個(gè) special group,有其對(duì)應(yīng)的空間(essential space),或者說(shuō) 5 維的流形上(essential manifold),當(dāng)有噪聲時(shí),得到的解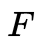 會(huì)在這個(gè)空間外。為了便于表達(dá),我們引入 normalized essential matrix 來(lái)消除尺度的干擾:
會(huì)在這個(gè)空間外。為了便于表達(dá),我們引入 normalized essential matrix 來(lái)消除尺度的干擾: 在后文我們提到的
在后文我們提到的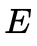 不特殊說(shuō)明都指的是normalized essential matrix.我們希望能在 essential space 中找到一個(gè)距離F最“近”的解,然后將F投影到這個(gè)解上,如下圖所示:
不特殊說(shuō)明都指的是normalized essential matrix.我們希望能在 essential space 中找到一個(gè)距離F最“近”的解,然后將F投影到這個(gè)解上,如下圖所示: 在說(shuō)明怎樣投影前,我們需要先給出三個(gè)定理:
在說(shuō)明怎樣投影前,我們需要先給出三個(gè)定理: 定理一描述了一個(gè)矩陣為 Essential Matrix 的充要條件。
定理一描述了一個(gè)矩陣為 Essential Matrix 的充要條件。 定理二描述了如何從 Essential Matrix 恢復(fù)到旋轉(zhuǎn)矩陣以及平移方向向量。這里需要注意的是,normalized essential matrix 可以消除尺度的干擾,但是不能消除符號(hào)的干擾,代數(shù)角度而言,E 和?E 都滿足Epipolar Constraint,因此實(shí)際我們能得到四組解。
定理二描述了如何從 Essential Matrix 恢復(fù)到旋轉(zhuǎn)矩陣以及平移方向向量。這里需要注意的是,normalized essential matrix 可以消除尺度的干擾,但是不能消除符號(hào)的干擾,代數(shù)角度而言,E 和?E 都滿足Epipolar Constraint,因此實(shí)際我們能得到四組解。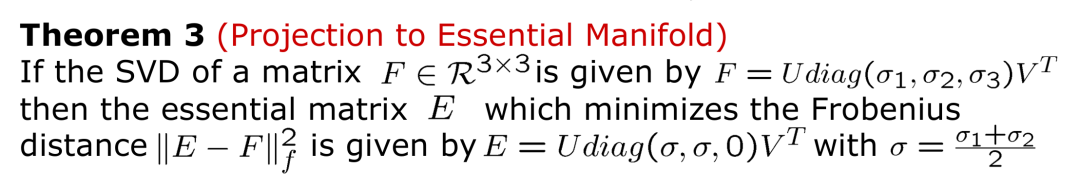 定理三給出了投影的方法,我們選擇F-norm作為投影距離的度量指標(biāo)。這里需要注意的是,
定理三給出了投影的方法,我們選擇F-norm作為投影距離的度量指標(biāo)。這里需要注意的是,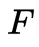 的SVD分解得到的
的SVD分解得到的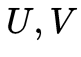 只滿足正交性,不能滿足行列式為+1的條件,當(dāng)?shù)玫降?/span>
只滿足正交性,不能滿足行列式為+1的條件,當(dāng)?shù)玫降?/span>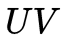 行列式為?1時(shí),我們會(huì)對(duì)其取負(fù),在后面我們會(huì)用代碼具體解釋。以上三個(gè)定理在馬老師的書(shū)里都有詳細(xì)證明,出于易讀性的考慮后續(xù)會(huì)單獨(dú)的整理到我的知乎上分享。在有了這三個(gè)定理之后,整個(gè)算法也就明朗了,流程如下:
行列式為?1時(shí),我們會(huì)對(duì)其取負(fù),在后面我們會(huì)用代碼具體解釋。以上三個(gè)定理在馬老師的書(shū)里都有詳細(xì)證明,出于易讀性的考慮后續(xù)會(huì)單獨(dú)的整理到我的知乎上分享。在有了這三個(gè)定理之后,整個(gè)算法也就明朗了,流程如下: 以上就是著名的八點(diǎn)法,你可以在許多資料上看到這個(gè)過(guò)程,本文的主要目的是梳理八點(diǎn)法的一些思路。我們引用一段 colmap 中的源碼來(lái)解讀上述過(guò)程:
以上就是著名的八點(diǎn)法,你可以在許多資料上看到這個(gè)過(guò)程,本文的主要目的是梳理八點(diǎn)法的一些思路。我們引用一段 colmap 中的源碼來(lái)解讀上述過(guò)程:
voidDecomposeEssentialMatrix(
const Eigen : : Matrix3d& E, Eigen : : Matrix3d? R1,
Eigen : : Matrix3d? R2, Eigen : : Vector3d? t )
{
// 根據(jù)對(duì)極約束得到的帶噪聲的E做SVD分解
Eigen::JacobiSVD svd(
E, Eigen : : ComputeFullU | Eigen : : ComputeFullV ) ;
Eigen::Matrix3d U = svd.matrixU();
Eigen::Matrix3d V = svd.matrixV().transpose();
// 保證行列式符號(hào)為正
if (U.determinant() < 0) {
U ?= ?1;
}
if (V.determinant() < 0) {
V ?= ?1;
}
Eigen : : Matrix3d W;
W<< 0, 1, 0, ?1, 0, 0, 0, 0, 1;
?R1 = U ? W ? V;
?R2=U?W.transpose() ?V;
?t = U. col (2). normalized ();
}
void PoseFromEssentialMatrix ( const Eigen : : Matrix3d& E,
const std : : vector& points1 ,
const std : : vector& points2 ,
Eigen : : Matrix3d? R, Eigen : : Vector3d? t ,
std : : vector? points3D ) { 7
CHECK_EQ(points1 . size () , points2 . size ());
Eigen::Matrix3d R1;
Eigen::Matrix3d R2;
DecomposeEssentialMatrix(E, &R1, &R2, t );
// Generate all possible projection matrix combinations.
const std : : array R_cmbs{{R1, R2, R1, R2}};
const std : : array t_cmbs{{?t , ?t , ??t , ??t }};
...
}
這里為什么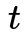 取
取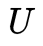 的最后一行可以留給讀者作為一個(gè)思考題,提示是
的最后一行可以留給讀者作為一個(gè)思考題,提示是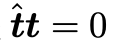 ,然后分析一下矩陣的秩。八點(diǎn)法十分簡(jiǎn)潔(當(dāng)然證明過(guò)程比較復(fù)雜),但是在實(shí)際使用過(guò)程中,還是會(huì)遇到許多問(wèn)題的,我們?cè)谝韵潞?jiǎn)要列舉:1. Number of points. 由于 Normalized Essential Matrix 的自由度為 5,在比較 general 的情況下,最少選取的 correspondence 點(diǎn)對(duì)為 5(Kruppa在 1913 年的時(shí)候給出了五點(diǎn)法,類似八點(diǎn)法會(huì)產(chǎn)生 4 個(gè)滿足對(duì)極約束的解,五點(diǎn)法會(huì)產(chǎn)生 10個(gè)解),因此選取多少點(diǎn)是一個(gè)需要實(shí)際使用中考慮的問(wèn)題。2. Number of solutions and positive depth constraint.雖然八點(diǎn)法給出了四對(duì)解,但是實(shí)際上只有一個(gè)正確解,那么其他三個(gè)解怎么排除呢?首先從代數(shù)層面,不要忘了最原始的表達(dá)式
,然后分析一下矩陣的秩。八點(diǎn)法十分簡(jiǎn)潔(當(dāng)然證明過(guò)程比較復(fù)雜),但是在實(shí)際使用過(guò)程中,還是會(huì)遇到許多問(wèn)題的,我們?cè)谝韵潞?jiǎn)要列舉:1. Number of points. 由于 Normalized Essential Matrix 的自由度為 5,在比較 general 的情況下,最少選取的 correspondence 點(diǎn)對(duì)為 5(Kruppa在 1913 年的時(shí)候給出了五點(diǎn)法,類似八點(diǎn)法會(huì)產(chǎn)生 4 個(gè)滿足對(duì)極約束的解,五點(diǎn)法會(huì)產(chǎn)生 10個(gè)解),因此選取多少點(diǎn)是一個(gè)需要實(shí)際使用中考慮的問(wèn)題。2. Number of solutions and positive depth constraint.雖然八點(diǎn)法給出了四對(duì)解,但是實(shí)際上只有一個(gè)正確解,那么其他三個(gè)解怎么排除呢?首先從代數(shù)層面,不要忘了最原始的表達(dá)式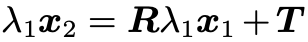 ,在這個(gè)表達(dá)式中隱藏了一個(gè)很關(guān)鍵的約束,深度值應(yīng)該為正,至于怎么求深度值是三角化部分的知識(shí)了,我們不在這里討論,如果你對(duì)上述過(guò)程熟悉,不難發(fā)現(xiàn)就是一個(gè)叉乘的技巧。基于這一約束我們可以將正確的解篩選出來(lái)。而從幾何層面來(lái)看,就是下面這張圖(From Multiple View Geometry in Computer Vision):
,在這個(gè)表達(dá)式中隱藏了一個(gè)很關(guān)鍵的約束,深度值應(yīng)該為正,至于怎么求深度值是三角化部分的知識(shí)了,我們不在這里討論,如果你對(duì)上述過(guò)程熟悉,不難發(fā)現(xiàn)就是一個(gè)叉乘的技巧。基于這一約束我們可以將正確的解篩選出來(lái)。而從幾何層面來(lái)看,就是下面這張圖(From Multiple View Geometry in Computer Vision): 3. Structure requirement: general position.當(dāng)觀測(cè)到的空間點(diǎn)滿足某些導(dǎo)致退化的條件時(shí)(called critical surfaces),使用八點(diǎn)法會(huì)遇到解不唯一的情況。一個(gè)典型的例子就是觀測(cè)點(diǎn)共面的情況,這種時(shí)候我們需要使用homography 來(lái)解決。4. Motion requirement: su?icient parallax.也就是說(shuō),平移量不能為0(為0時(shí)也要使用 homography)。需要十分小心的是,在沒(méi)有平移移動(dòng)且匹配十分 noise 的時(shí)候,八點(diǎn)法依舊會(huì)得到一個(gè)很奇怪的平移部分的解,而這個(gè)解是毫無(wú)意義的。5. Multiple motion hypotheses.運(yùn)動(dòng)物體場(chǎng)景,這又是另一個(gè)問(wèn)題了。03結(jié)語(yǔ)Essential Matrix 之所以叫 Essential Matrix,就是因?yàn)樗匾? 馬老師花了4節(jié)課的時(shí)間,介紹two view geometry的內(nèi)容, 可見(jiàn)其重要性。目前學(xué)術(shù)的研究主要在于recognition的問(wèn)題了,也有許多工作還是聚焦在end to end的執(zhí)著,當(dāng)然這只是我個(gè)人的一些粗淺的看法。審核編輯 :李倩
3. Structure requirement: general position.當(dāng)觀測(cè)到的空間點(diǎn)滿足某些導(dǎo)致退化的條件時(shí)(called critical surfaces),使用八點(diǎn)法會(huì)遇到解不唯一的情況。一個(gè)典型的例子就是觀測(cè)點(diǎn)共面的情況,這種時(shí)候我們需要使用homography 來(lái)解決。4. Motion requirement: su?icient parallax.也就是說(shuō),平移量不能為0(為0時(shí)也要使用 homography)。需要十分小心的是,在沒(méi)有平移移動(dòng)且匹配十分 noise 的時(shí)候,八點(diǎn)法依舊會(huì)得到一個(gè)很奇怪的平移部分的解,而這個(gè)解是毫無(wú)意義的。5. Multiple motion hypotheses.運(yùn)動(dòng)物體場(chǎng)景,這又是另一個(gè)問(wèn)題了。03結(jié)語(yǔ)Essential Matrix 之所以叫 Essential Matrix,就是因?yàn)樗匾? 馬老師花了4節(jié)課的時(shí)間,介紹two view geometry的內(nèi)容, 可見(jiàn)其重要性。目前學(xué)術(shù)的研究主要在于recognition的問(wèn)題了,也有許多工作還是聚焦在end to end的執(zhí)著,當(dāng)然這只是我個(gè)人的一些粗淺的看法。審核編輯 :李倩
聲明:本文內(nèi)容及配圖由入駐作者撰寫或者入駐合作網(wǎng)站授權(quán)轉(zhuǎn)載。文章觀點(diǎn)僅代表作者本人,不代表電子發(fā)燒友網(wǎng)立場(chǎng)。文章及其配圖僅供工程師學(xué)習(xí)之用,如有內(nèi)容侵權(quán)或者其他違規(guī)問(wèn)題,請(qǐng)聯(lián)系本站處理。
舉報(bào)投訴
-
相機(jī)
+關(guān)注
關(guān)注
4文章
1468瀏覽量
54697 -
3D視覺(jué)
+關(guān)注
關(guān)注
4文章
452瀏覽量
28261 -
視圖
+關(guān)注
關(guān)注
0文章
140瀏覽量
6806
原文標(biāo)題:雙視圖幾何:你真的理解嗎?
文章出處:【微信號(hào):3D視覺(jué)工坊,微信公眾號(hào):3D視覺(jué)工坊】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
熱點(diǎn)推薦
如何通俗理解視覺(jué)定位?帶你看懂對(duì)極幾何與基本矩陣
本文為大家介紹對(duì)極幾何與基本矩陣這兩個(gè)視覺(jué)定位原理。對(duì)極幾何提到對(duì)極幾何,一定是對(duì)二幅圖像而言,對(duì)極幾何實(shí)際上是“兩幅圖像之間的對(duì)極幾何”,
發(fā)表于 06-01 08:00
頻率和時(shí)序,你是否真的了解呢?
影響內(nèi)存的關(guān)鍵因素是哪些?頻率和時(shí)序,你是否真的了解呢?時(shí)序與頻率有什么區(qū)別?哪個(gè)對(duì)內(nèi)存性能影響大?
發(fā)表于 06-18 07:15
PCB設(shè)計(jì)規(guī)則你知幾何
PCB設(shè)計(jì)規(guī)則你知幾何,20個(gè)PCB設(shè)計(jì)規(guī)則送給你。
發(fā)表于 11-11 07:16
你真的懂Word嗎
在日常辦公當(dāng)中, Word文檔就是我們最常用的軟件之一。用它我們寫論文、寫方案、寫小說(shuō)等等。但是,你真的懂Word嗎?其實(shí),Word軟件背后,還有一大批隱藏技能你不知道。掌握他們,你將
發(fā)表于 01-12 08:22
如何才能看懂電子元器件規(guī)格書(shū)里的三視圖
電子元器件規(guī)格書(shū)里的三視圖,或者電子零件規(guī)格書(shū)里的三視圖其實(shí)是三視圖里面最簡(jiǎn)單不過(guò)的三視圖,我們還是要了解一些三視圖的基本概念,這樣對(duì)我們更
發(fā)表于 11-09 15:27
?3.6w次閱讀
第16章iOS視圖及視圖控制器
16.1 iOS的窗口與視圖介紹
16.2 iOS控件
16.3 iOS視圖控制器
16.4視圖控制器應(yīng)用實(shí)例
發(fā)表于 04-11 11:12
?0次下載
多表物化視圖的需求分析及實(shí)現(xiàn)應(yīng)用設(shè)計(jì)
要了解物化視圖可以先了解視圖的概念。視圖是一個(gè)虛擬表(也可以認(rèn)為是一條語(yǔ)句),基于它創(chuàng)建時(shí)指定的查詢語(yǔ)句返回的結(jié)果集。而物化視圖則是將這個(gè)虛擬表進(jìn)行實(shí)體化,其本身可以
基于幾何變換器的2D-to-BEV視圖轉(zhuǎn)換學(xué)習(xí)
BEV感知是自動(dòng)駕駛的重要趨勢(shì)。常規(guī)的自動(dòng)駕駛算法方法基于在前視圖或透視圖中執(zhí)行檢測(cè)、分割、跟蹤,而在BEV中可表示周圍場(chǎng)景,相對(duì)而言更加直觀,并且在BEV中表示目標(biāo)對(duì)于后續(xù)模塊最為理想。
發(fā)表于 06-06 17:47
?2165次閱讀
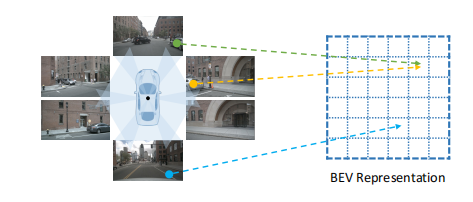





 雙視圖幾何:你真的理解嗎?
雙視圖幾何:你真的理解嗎?











評(píng)論