到目前為止，我們的序列學習任務的工作示例是語言建模，我們的目標是在給定序列中所有先前標記的情況下預測下一個標記。在這種情況下，我們只希望以左向上下文為條件，因此標準 RNN 的單向鏈接似乎是合適的。然而，還有許多其他序列學習任務上下文，在這些上下文中，在向左和向右上下文的每個時間步調整預測是非常好的。例如，考慮詞性檢測。在評估與給定詞相關的詞性時，為什么我們不應該考慮兩個方向的上下文？

另一項常見任務（通常在針對感興趣的實際任務微調模型之前用作預訓練練習）是屏蔽文本文檔中的隨機標記，然后訓練序列模型以預測缺失標記的值。請注意，根據空白后面的內容，缺失標記的可能值會發生顯著變化：

我是___。

我___餓了。

我___餓了，我能吃半頭豬。

在第一句話中，“快樂”似乎是一個可能的候選者。“不”和“非常”這兩個詞在第二句中似乎說得通，但“不”與第三句似乎格格不入。

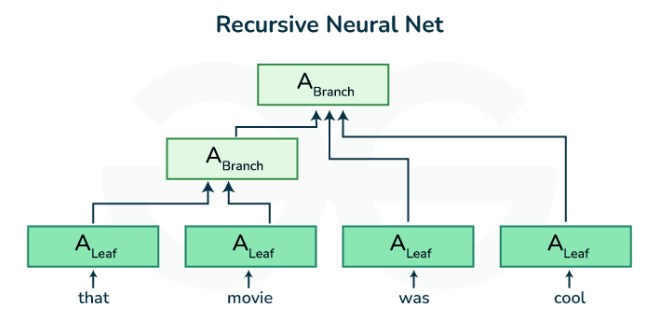
幸運的是，一種簡單的技術可以將任何單向 RNN 轉換為雙向 RNN （Schuster 和 Paliwal，1997）。我們簡單地實現兩個單向 RNN 層，它們以相反的方向鏈接在一起并作用于相同的輸入（圖 10.4.1）。對于第一個 RNN 層，第一個輸入是x1最后的輸入是 xT，但是對于第二個 RNN 層，第一個輸入是 xT最后的輸入是x1. 為了產生這個雙向 RNN 層的輸出，我們只需將兩個底層單向 RNN 層的相應輸出連接在一起。

圖 10.4.1雙向 RNN 的架構。

正式地為任何時間步長t，我們考慮一個小批量輸入 Xt∈Rn×d（示例數量： n，每個示例中的輸入數量：d) 并令隱藏層激活函數為?. 在雙向架構中，這個時間步長的前向和后向隱藏狀態是H→t∈Rn×h 和H←t∈Rn×h，分別在哪里h是隱藏單元的數量。前向和后向隱藏狀態更新如下：

(10.4.1)H→t=?(XtWxh(f)+H→t?1Whh(f)+bh(f)),H←t=?(XtWxh(b)+H←t+1Whh(b)+bh(b)),

權重在哪里 Wxh(f)∈Rd×h,Whh(f)∈Rh×h,Wxh(b)∈Rd×h,andWhh(b)∈Rh×h, 和偏見bh(f)∈R1×h和 bh(b)∈R1×h都是模型參數。

接下來，我們連接前向和后向隱藏狀態 H→t和 H←t獲得隱藏狀態 Ht∈Rn×2h送入輸出層。在具有多個隱藏層的深度雙向 RNN 中，此類信息作為輸入傳遞到下一個雙向層。最后，輸出層計算輸出 Ot∈Rn×q（輸出數量： q):

(10.4.2)Ot=HtWhq+bq.

這里，權重矩陣 Whq∈R2h×q和偏見 bq∈R1×q是輸出層的模型參數。雖然從技術上講，兩個方向可以有不同數量的隱藏單元，但在實踐中很少做出這種設計選擇。我們現在演示雙向 RNN 的簡單實現。

import torch
from torch import nn
from d2l import torch as d2l

from mxnet import np, npx
from mxnet.gluon import rnn
from d2l import mxnet as d2l

npx.set_np()

from jax import numpy as jnp
from d2l import jax as d2l

No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

import tensorflow as tf
from d2l import tensorflow as d2l

10.4.1。從零開始實施

要從頭開始實現雙向 RNN，我們可以包含兩個RNNScratch具有獨立可學習參數的單向實例。

class BiRNNScratch(d2l.Module):
  def __init__(self, num_inputs, num_hiddens, sigma=0.01):
    super().__init__()
    self.save_hyperparameters()
    self.f_rnn = d2l.RNNScratch(num_inputs, num_hiddens, sigma)
    self.b_rnn = d2l.RNNScratch(num_inputs, num_hiddens, sigma)
    self.num_hiddens *= 2 # The output dimension will be doubled

class BiRNNScratch(d2l.Module):
  def __init__(self, num_inputs, num_hiddens, sigma=0.01):
    super().__init__()
    self.save_hyperparameters()
    self.f_rnn = d2l.RNNScratch(num_inputs, num_hiddens, sigma)
    self.b_rnn = d2l.RNNScratch(num_inputs, num_hiddens, sigma)
    self.num_hiddens *= 2 # The output dimension will be doubled

class BiRNNScratch(d2l.Module):
  num_inputs: int
  num_hiddens: int
  sigma: float = 0.01

  def setup(self):
    self.f_rnn = d2l.RNNScratch(num_inputs, num_hiddens, sigma)
    self.b_rnn = d2l.RNNScratch(num_inputs, num_hiddens, sigma)
    self.num_hiddens *= 2 # The output dimension will be doubled

class BiRNNScratch(d2l.Module):
  def __init__(self, num_inputs, num_hiddens, sigma=0.01):
    super().__init__()
    self.save_hyperparameters()
    self.f_rnn = d2l.RNNScratch(num_inputs, num_hiddens, sigma)
    self.b_rnn = d2l.RNNScratch(num_inputs, num_hiddens, sigma)
    self.num_hiddens *= 2 # The output dimension will be doubled

前向和后向 RNN 的狀態分別更新，而這兩個 RNN 的輸出被連接起來。

@d2l.add_to_class(BiRNNScratch)
def forward(self, inputs, Hs=None):
  f_H, b_H = Hs if Hs is not None else (None, None)
  f_outputs, f_H = self.f_rnn(inputs, f_H)
  b_outputs, b_H = self.b_rnn(reversed(inputs), b_H)
  outputs = [torch.cat((f, b), -1) for f, b in zip(
    f_outputs, reversed(b_outputs))]
  return outputs, (f_H, b_H)

@d2l.add_to_class(BiRNNScratch)
def forward(self, inputs, Hs=None):
  f_H, b_H = Hs if Hs is not None else (None, None)
  f_outputs, f_H = self.f_rnn(inputs, f_H)
  b_outputs, b_H = self.b_rnn(reversed(inputs), b_H)
  outputs = [np.concatenate((f, b), -1) for f, b in zip(
    f_outputs, reversed(b_outputs))]
  return outputs, (f_H, b_H)

@d2l.add_to_class(BiRNNScratch)
def forward(self, inputs, Hs=None):
  f_H, b_H = Hs if Hs is not None else (None, None)
  f_outputs, f_H = self.f_rnn(inputs, f_H)
  b_outputs, b_H = self.b_rnn(reversed(inputs), b_H)
  outputs = [jnp.concatenate((f, b), -1) for f, b in zip(
    f_outputs, reversed(b_outputs))]
  return outputs, (f_H, b_H)

@d2l.add_to_class(BiRNNScratch)
def forward(self, inputs, Hs=None):
  f_H, b_H = Hs if Hs is not None else (None, None)
  f_outputs, f_H = self.f_rnn(inputs, f_H)
  b_outputs, b_H = self.b_rnn(reversed(inputs), b_H)
  outputs = [tf.concat((f, b), -1) for f, b in zip(
    f_outputs, reversed(b_outputs))]
  return outputs, (f_H, b_H)

10.4.2。簡潔的實現

使用高級 API，我們可以更簡潔地實現雙向 RNN。這里我們以一個 GRU 模型為例。

class BiGRU(d2l.RNN):
  def __init__(self, num_inputs, num_hiddens):
    d2l.Module.__init__(self)
    self.save_hyperparameters()
    self.rnn = nn.GRU(num_inputs, num_hiddens, bidirectional=True)
    self.num_hiddens *= 2

Using the high-level APIs, we can implement bidirectional RNNs more concisely. Here we take a GRU model as an example.

class BiGRU(d2l.RNN):
  def __init__(self, num_inputs, num_hiddens):
    d2l.Module.__init__(self)
    self.save_hyperparameters()
    self.rnn = rnn.GRU(num_hiddens, bidirectional=True)
    self.num_hiddens *= 2

Flax API does not offer RNN layers and hence there is no notion of any bidirectional argument. One needs to manually reverse the inputs as shown in the scratch implementation, if a bidirectional layer is needed.

Using the high-level APIs, we can implement bidirectional RNNs more concisely. Here we take a GRU model as an example.

10.4.3。概括

在雙向 RNN 中，每個時間步的隱藏狀態同時由當前時間步之前和之后的數據確定。雙向 RNN 主要用于序列編碼和給定雙向上下文的觀察估計。由于長梯度鏈，雙向 RNN 的訓練成本非常高。

10.4.4。練習

如果不同方向使用不同數量的隱藏單元，形狀將如何Ht改變？

設計具有多個隱藏層的雙向 RNN。

多義現象在自然語言中很常見。例如，“銀行”一詞在“我去銀行存款”和“我去銀行坐下”的語境中有不同的含義。我們如何設計一個神經網絡模型，以便在給定上下文序列和一個詞的情況下，返回該詞在上下文中的向量表示？哪種類型的神經架構更適合處理多義詞？