作者:Onepagecode
來源:DeepHub IMBA
神經(jīng)網(wǎng)絡(luò)在訓(xùn)練時的優(yōu)化首先是對模型的當(dāng)前狀態(tài)進(jìn)行誤差估計(jì),然后為了減少下一次評估的誤差,需要使用一個能夠表示錯誤函數(shù)對權(quán)重進(jìn)行更新,這個函數(shù)被稱為損失函數(shù)。
損失函數(shù)的選擇與神經(jīng)網(wǎng)絡(luò)模型從示例中學(xué)習(xí)的特定預(yù)測建模問題(例如分類或回歸)有關(guān)。在本文中我們將介紹常用的一些損失函數(shù),包括:
回歸模型的均方誤差損失
二元分類模型的交叉熵和hinge 損失
回歸模型的損失函數(shù)
回歸預(yù)測模型主要是用來預(yù)測連續(xù)的數(shù)值。所以我們將使用 scikit-learn的 make_regression() 函數(shù)來生成一些模擬數(shù)據(jù),并使用這些數(shù)據(jù)構(gòu)建回歸模型。我們將生成 20 個輸入特征:其中 10 個特征將是有意義的,但 10 個與問題無關(guān)。并且隨機(jī)生成 1,000 個示例。并且指定隨機(jī)種子,所以無論何時運(yùn)行代碼都會生成相同的 1,000 個示例。 將實(shí)值輸入和輸出變量縮放到一個合理的范圍通常可以提高神經(jīng)網(wǎng)絡(luò)的性能。所以我們要對對數(shù)據(jù)進(jìn)行標(biāo)準(zhǔn)化處理。StandardScaler也可以在scikit-learn庫中找到,為了簡化問題我們將在將所有數(shù)據(jù)分割為訓(xùn)練集和測試集之前對其進(jìn)行縮放。
將實(shí)值輸入和輸出變量縮放到一個合理的范圍通常可以提高神經(jīng)網(wǎng)絡(luò)的性能。所以我們要對對數(shù)據(jù)進(jìn)行標(biāo)準(zhǔn)化處理。StandardScaler也可以在scikit-learn庫中找到,為了簡化問題我們將在將所有數(shù)據(jù)分割為訓(xùn)練集和測試集之前對其進(jìn)行縮放。 然后平均分割訓(xùn)練和驗(yàn)證集
然后平均分割訓(xùn)練和驗(yàn)證集 為了介紹不同的損失函數(shù),我們將開發(fā)一個小型多層感知器(MLP)模型。根據(jù)問題定義,有20個特征作為輸入,經(jīng)過我們的模型。需要要預(yù)測的一個實(shí)值,所以輸出層將有一個節(jié)點(diǎn)。
為了介紹不同的損失函數(shù),我們將開發(fā)一個小型多層感知器(MLP)模型。根據(jù)問題定義,有20個特征作為輸入,經(jīng)過我們的模型。需要要預(yù)測的一個實(shí)值,所以輸出層將有一個節(jié)點(diǎn)。 我們使用SGD進(jìn)行優(yōu)化,并且學(xué)習(xí)率為0.01,動量為0.9,兩者都是合理的默認(rèn)值。訓(xùn)練將進(jìn)行100個輪,測試集將在每個階段結(jié)束時進(jìn)行評估,并且繪制學(xué)習(xí)曲線。
我們使用SGD進(jìn)行優(yōu)化,并且學(xué)習(xí)率為0.01,動量為0.9,兩者都是合理的默認(rèn)值。訓(xùn)練將進(jìn)行100個輪,測試集將在每個階段結(jié)束時進(jìn)行評估,并且繪制學(xué)習(xí)曲線。 模型完成后就可以進(jìn)行損失函數(shù)的介紹:MSE回歸問題最常使用的是均方誤差損失(MSE)。當(dāng)目標(biāo)變量的分布為高斯分布時,它是最大似然推理下的首選損失函數(shù)。所以只有當(dāng)你有一個更好的理由時,才應(yīng)該改變?yōu)槠渌麚p失函數(shù)。如果在 Keras 中編譯模型時將“mse”或“mean_squared_error”指定為損失函數(shù),則使用均方誤差損失函數(shù)。
模型完成后就可以進(jìn)行損失函數(shù)的介紹:MSE回歸問題最常使用的是均方誤差損失(MSE)。當(dāng)目標(biāo)變量的分布為高斯分布時,它是最大似然推理下的首選損失函數(shù)。所以只有當(dāng)你有一個更好的理由時,才應(yīng)該改變?yōu)槠渌麚p失函數(shù)。如果在 Keras 中編譯模型時將“mse”或“mean_squared_error”指定為損失函數(shù),則使用均方誤差損失函數(shù)。 下面的代碼是上述回歸問題的完整示例。
下面的代碼是上述回歸問題的完整示例。 在運(yùn)行示例的第一步中,打印了模型的訓(xùn)練和測試數(shù)據(jù)集的均方誤差,因?yàn)楸A袅?位小數(shù),所以顯示為0.000
在運(yùn)行示例的第一步中,打印了模型的訓(xùn)練和測試數(shù)據(jù)集的均方誤差,因?yàn)楸A袅?位小數(shù),所以顯示為0.000 從下圖中可以看出,模型收斂速度相當(dāng)快,訓(xùn)練和測試性能保持不變。根據(jù)模型的性能和收斂特性,均方誤差是回歸問題的一個很好的選擇。
從下圖中可以看出,模型收斂速度相當(dāng)快,訓(xùn)練和測試性能保持不變。根據(jù)模型的性能和收斂特性,均方誤差是回歸問題的一個很好的選擇。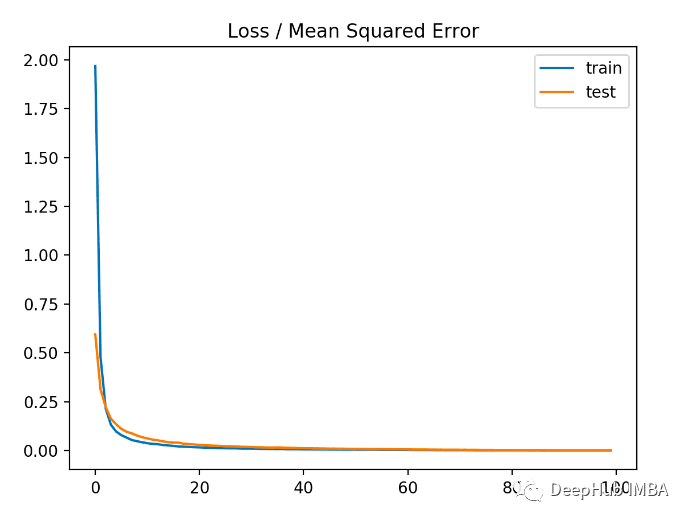 MSLE在具有廣泛值的回歸問題中,可能不希望在預(yù)測大值時像均方誤差那樣對模型進(jìn)行懲罰。所以可以通過首先計(jì)算每個預(yù)測值的自然對數(shù)來計(jì)算均方誤差。這種損失稱為 MSLE,或均方對數(shù)誤差。當(dāng)預(yù)測值出現(xiàn)較大差異時,它具有放松懲罰效果的效果。當(dāng)模型直接預(yù)測未縮放的數(shù)量時,它可能是更合適的損失度量。keras中使用“mean_squared_logarithmic_error”作為損失函數(shù)
MSLE在具有廣泛值的回歸問題中,可能不希望在預(yù)測大值時像均方誤差那樣對模型進(jìn)行懲罰。所以可以通過首先計(jì)算每個預(yù)測值的自然對數(shù)來計(jì)算均方誤差。這種損失稱為 MSLE,或均方對數(shù)誤差。當(dāng)預(yù)測值出現(xiàn)較大差異時,它具有放松懲罰效果的效果。當(dāng)模型直接預(yù)測未縮放的數(shù)量時,它可能是更合適的損失度量。keras中使用“mean_squared_logarithmic_error”作為損失函數(shù) 在下面的示例是使用MSLE損失函數(shù)的完整代碼。
在下面的示例是使用MSLE損失函數(shù)的完整代碼。 該模型在訓(xùn)練和測試數(shù)據(jù)集上的MSE都略差。這是由于目標(biāo)變量的分布是一個標(biāo)準(zhǔn)的高斯分布,說明我們的這個損失函數(shù)可能不是很適合這個問題。
該模型在訓(xùn)練和測試數(shù)據(jù)集上的MSE都略差。這是由于目標(biāo)變量的分布是一個標(biāo)準(zhǔn)的高斯分布,說明我們的這個損失函數(shù)可能不是很適合這個問題。 下圖顯示各訓(xùn)練輪次的對比MSE收斂得很好,但MSE可能過擬合了,因?yàn)樗鼜?0輪開始下降變得變換并且開始上升。
下圖顯示各訓(xùn)練輪次的對比MSE收斂得很好,但MSE可能過擬合了,因?yàn)樗鼜?0輪開始下降變得變換并且開始上升。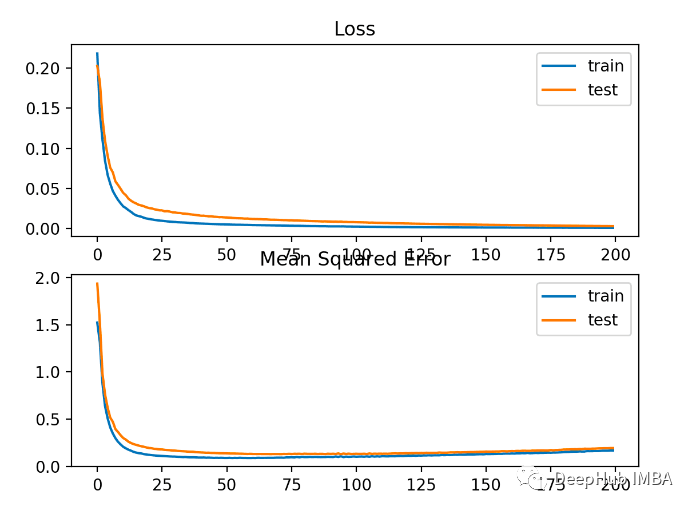 MAE根據(jù)回歸問題,目標(biāo)變量的分布可能主要是高斯分布,但可能包含異常值,例如 遠(yuǎn)離平均值的大值或小值。在這種情況下,平均絕對誤差或 MAE 損失是一個合適的損失函數(shù),因?yàn)樗鼘Ξ惓V蹈€(wěn)健。考慮到實(shí)際值與預(yù)測值的絕對差值,計(jì)算為平均值。使用“mean_absolute_error”損失函數(shù)
MAE根據(jù)回歸問題,目標(biāo)變量的分布可能主要是高斯分布,但可能包含異常值,例如 遠(yuǎn)離平均值的大值或小值。在這種情況下,平均絕對誤差或 MAE 損失是一個合適的損失函數(shù),因?yàn)樗鼘Ξ惓V蹈€(wěn)健。考慮到實(shí)際值與預(yù)測值的絕對差值,計(jì)算為平均值。使用“mean_absolute_error”損失函數(shù) 這是使用MAE的完整代碼
這是使用MAE的完整代碼 結(jié)果如下
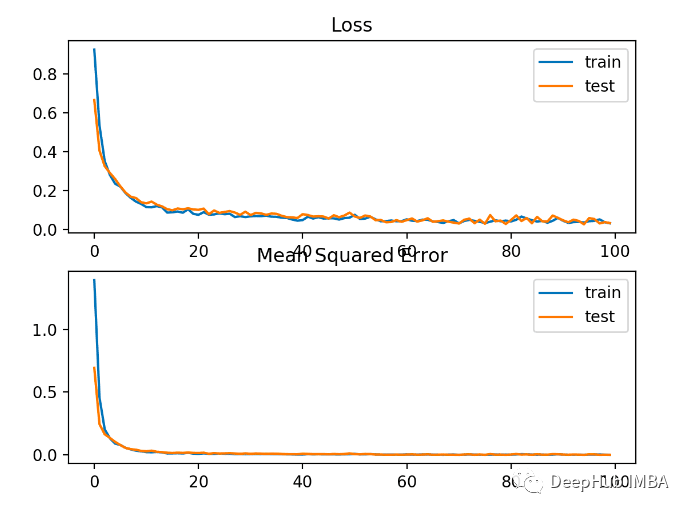
結(jié)果如下 下圖可以看到,MAE確實(shí)收斂了但它有一個顛簸的過程。MAE在這種情況下也不是很適合,因?yàn)槟繕?biāo)變量是一個沒有大離群值的高斯函數(shù)。
下圖可以看到,MAE確實(shí)收斂了但它有一個顛簸的過程。MAE在這種情況下也不是很適合,因?yàn)槟繕?biāo)變量是一個沒有大離群值的高斯函數(shù)。
二元分類的損失函數(shù)
二元分類問題是預(yù)測建模問題中兩個標(biāo)簽中的一個。這個問題被定義為預(yù)測第一個或第二個類的值為0或1,一般情況下通常被實(shí)現(xiàn)為預(yù)測屬于類值1的的概率。我們也是使用sklearn生成數(shù)據(jù)這里使用圓問題,它有一個二維平面,有兩個同心圓,其中外圓上的點(diǎn)屬于類0,內(nèi)圓上的點(diǎn)屬于類1。為了使學(xué)習(xí)更具挑戰(zhàn)性,我們還在樣本中加入了統(tǒng)計(jì)噪聲。樣本量為1000,并加入10%的統(tǒng)計(jì)噪聲。 數(shù)據(jù)集的散點(diǎn)圖可以幫助我們理解正在建模的問題。下面列出的是一個完整的示例。
數(shù)據(jù)集的散點(diǎn)圖可以幫助我們理解正在建模的問題。下面列出的是一個完整的示例。 散點(diǎn)圖如下,其中輸入變量確定點(diǎn)的位置,顏色為類值。0是藍(lán)色的,1是橙色的。
散點(diǎn)圖如下,其中輸入變量確定點(diǎn)的位置,顏色為類值。0是藍(lán)色的,1是橙色的。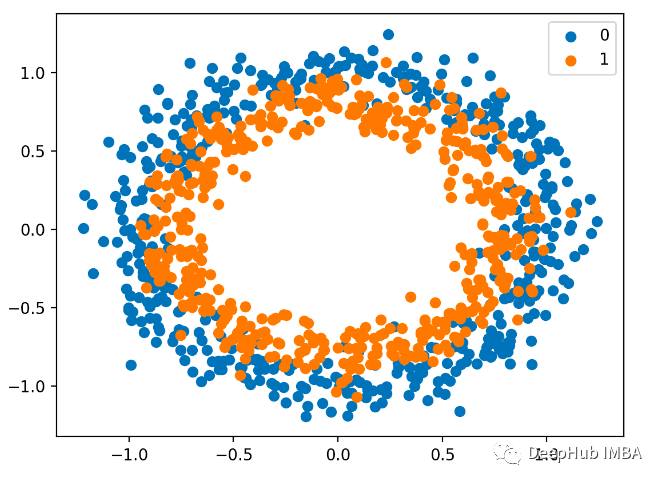 這里還是一半用于訓(xùn)練,一半用于測試,
這里還是一半用于訓(xùn)練,一半用于測試, 我們還是定義一個簡單的MLP模型,
我們還是定義一個簡單的MLP模型, 使用SGD優(yōu)化,學(xué)習(xí)率為0.01,動量為0.99。
使用SGD優(yōu)化,學(xué)習(xí)率為0.01,動量為0.99。 模型訓(xùn)練200輪進(jìn)行擬合,并根據(jù)損失和準(zhǔn)確性評估模型的性能。
模型訓(xùn)練200輪進(jìn)行擬合,并根據(jù)損失和準(zhǔn)確性評估模型的性能。 BCEBCE是用于解決的二元分類問題默認(rèn)損失函數(shù)。在最大似然推理框架下,它是首選損失函數(shù)。對于第1類的預(yù)測,交叉熵計(jì)算一個分?jǐn)?shù),該分?jǐn)?shù)總結(jié)了實(shí)際和預(yù)測概率分布之間的平均差異。在編譯Keras模型時,可以指定binary_crossentropy作為損失函數(shù)。
BCEBCE是用于解決的二元分類問題默認(rèn)損失函數(shù)。在最大似然推理框架下,它是首選損失函數(shù)。對于第1類的預(yù)測,交叉熵計(jì)算一個分?jǐn)?shù),該分?jǐn)?shù)總結(jié)了實(shí)際和預(yù)測概率分布之間的平均差異。在編譯Keras模型時,可以指定binary_crossentropy作為損失函數(shù)。 為了預(yù)測類1的概率,輸出層必須包含一個節(jié)點(diǎn)和一個' sigmoid '激活。
為了預(yù)測類1的概率,輸出層必須包含一個節(jié)點(diǎn)和一個' sigmoid '激活。 下面是完整的代碼:
下面是完整的代碼: 該模型對問題的學(xué)習(xí)相對較好,在測試數(shù)據(jù)集上的準(zhǔn)確率為83%,準(zhǔn)確率為85%。分?jǐn)?shù)之間存在一定程度的重疊,表明模型既不是過擬合也不是欠擬合。下圖中所示,訓(xùn)練效果很好。由于概率分布之間的誤差是連續(xù)的,損失圖是平滑的,而精度線圖顯示出凹凸不平,因?yàn)橛?xùn)練和測試集中的例子只能被預(yù)測為正確或不正確,提供的顆粒信息較少。
該模型對問題的學(xué)習(xí)相對較好,在測試數(shù)據(jù)集上的準(zhǔn)確率為83%,準(zhǔn)確率為85%。分?jǐn)?shù)之間存在一定程度的重疊,表明模型既不是過擬合也不是欠擬合。下圖中所示,訓(xùn)練效果很好。由于概率分布之間的誤差是連續(xù)的,損失圖是平滑的,而精度線圖顯示出凹凸不平,因?yàn)橛?xùn)練和測試集中的例子只能被預(yù)測為正確或不正確,提供的顆粒信息較少。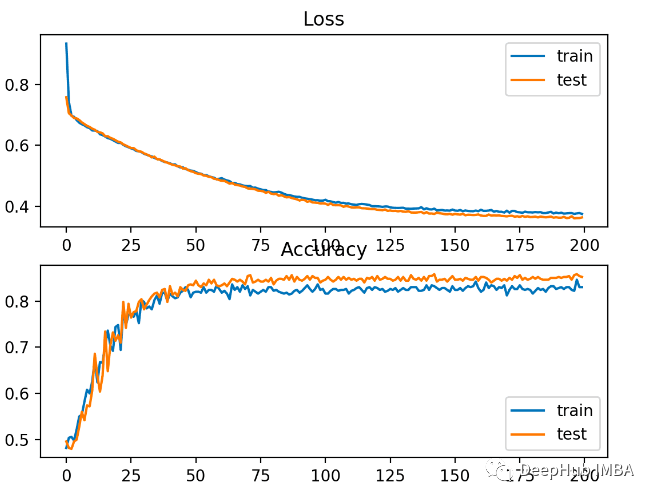 Hinge支持向量機(jī) (SVM) 模型使用Hinge 損失函數(shù)作為交叉熵的替代來解決二元分類問題。目標(biāo)值在是集合 [-1, 1] ,旨在與二進(jìn)制分類一起使用。如果實(shí)際類別值和預(yù)測類別值的符號不同,則Hinge會得到更大的誤差。在二元分類問題上它有時比交叉熵更好。作為第一步,我們必須將目標(biāo)變量的值修改為集合 {-1, 1}。
Hinge支持向量機(jī) (SVM) 模型使用Hinge 損失函數(shù)作為交叉熵的替代來解決二元分類問題。目標(biāo)值在是集合 [-1, 1] ,旨在與二進(jìn)制分類一起使用。如果實(shí)際類別值和預(yù)測類別值的符號不同,則Hinge會得到更大的誤差。在二元分類問題上它有時比交叉熵更好。作為第一步,我們必須將目標(biāo)變量的值修改為集合 {-1, 1}。 keras中它被稱為' hinge '。
keras中它被稱為' hinge '。 在網(wǎng)絡(luò)的輸出層中,必須使用tanh激活函數(shù)的單個節(jié)點(diǎn)以輸出介于 -1 和 1 之間的單個值。
在網(wǎng)絡(luò)的輸出層中,必須使用tanh激活函數(shù)的單個節(jié)點(diǎn)以輸出介于 -1 和 1 之間的單個值。 下面是完整代碼:
下面是完整代碼: 比交叉熵略差的性能,在訓(xùn)練和測試集上的準(zhǔn)確性不到80%。
比交叉熵略差的性能,在訓(xùn)練和測試集上的準(zhǔn)確性不到80%。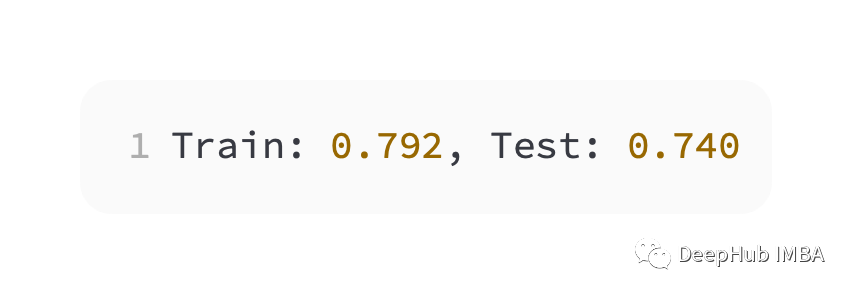 下圖可以看出,模型已經(jīng)收斂,分類精度圖表明也已經(jīng)收斂。
下圖可以看出,模型已經(jīng)收斂,分類精度圖表明也已經(jīng)收斂。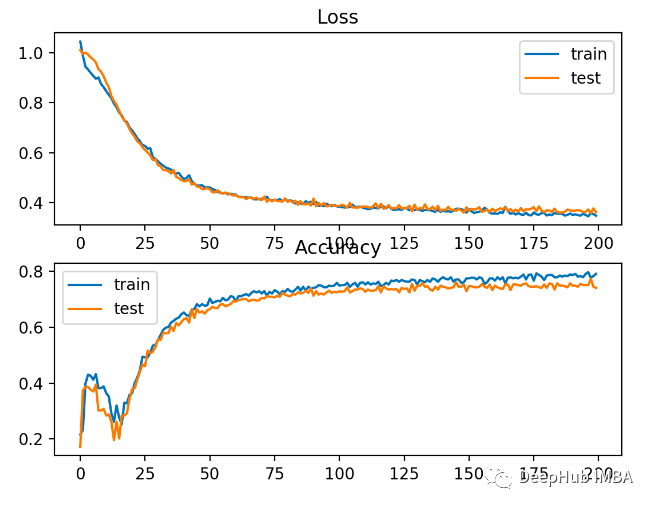 可以看到這個問題還是BCE比較好,這里可能的原因就是因?yàn)槲覀冇幸恍┰肼朁c(diǎn)導(dǎo)致的。
可以看到這個問題還是BCE比較好,這里可能的原因就是因?yàn)槲覀冇幸恍┰肼朁c(diǎn)導(dǎo)致的。
-
深度學(xué)習(xí)
+關(guān)注
關(guān)注
73文章
5557瀏覽量
122653
發(fā)布評論請先 登錄





 訓(xùn)練深度學(xué)習(xí)神經(jīng)網(wǎng)絡(luò)的常用5個損失函數(shù)
訓(xùn)練深度學(xué)習(xí)神經(jīng)網(wǎng)絡(luò)的常用5個損失函數(shù)











評論