在結(jié)構(gòu)中開孔以符合某種工程需求是工程上常見的現(xiàn)象，例如機(jī)械結(jié)構(gòu)中連接件、以及隧洞開挖、水利工程中的泄洪口等，而確定孔邊應(yīng)力分布，進(jìn)而對開孔構(gòu)件進(jìn)行強(qiáng)度校核，包括剛度校核、穩(wěn)定性判定是確保各類開孔工程安全的基礎(chǔ)。針對于這一問題，巴黎綜合理工學(xué)院的兩位校友拉梅（Gabriel Lame, 1795-1870）和克拉貝隆（Emile Clapeyron,1799-1864）于1831年率先得到了薄壁圓筒同時受內(nèi)壓和外壓的解，這為結(jié)構(gòu)開孔問題做出了奠基性工作。

設(shè)有一薄壁圓筒，受內(nèi)壓為qa，受外壓為qb，圓筒的內(nèi)半徑為a，外半徑為b，如圖2所示。在這一問題中，圓環(huán)為軸對稱，同時載荷也為軸對稱，該問題為（平面）軸對稱問題，其應(yīng)力、應(yīng)變、形變位移只是ρ的函數(shù)。

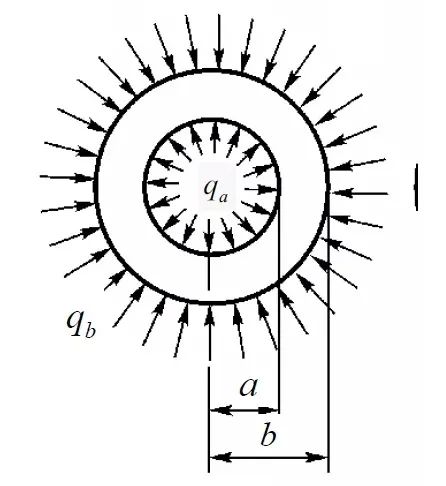
圖2 受內(nèi)外均勻壓力的薄壁圓筒

在這種情況下，若采用極坐標(biāo)系下應(yīng)力函數(shù)法求解，用應(yīng)力函數(shù)表達(dá)應(yīng)力分量可作如下簡化

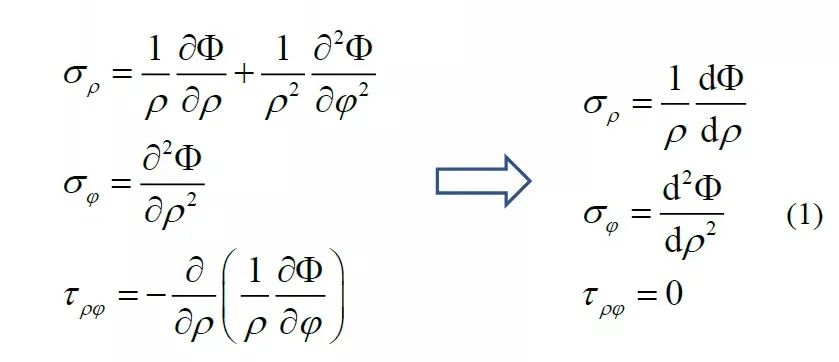
由極坐標(biāo)下的相容方程推導(dǎo)應(yīng)力函數(shù)，有

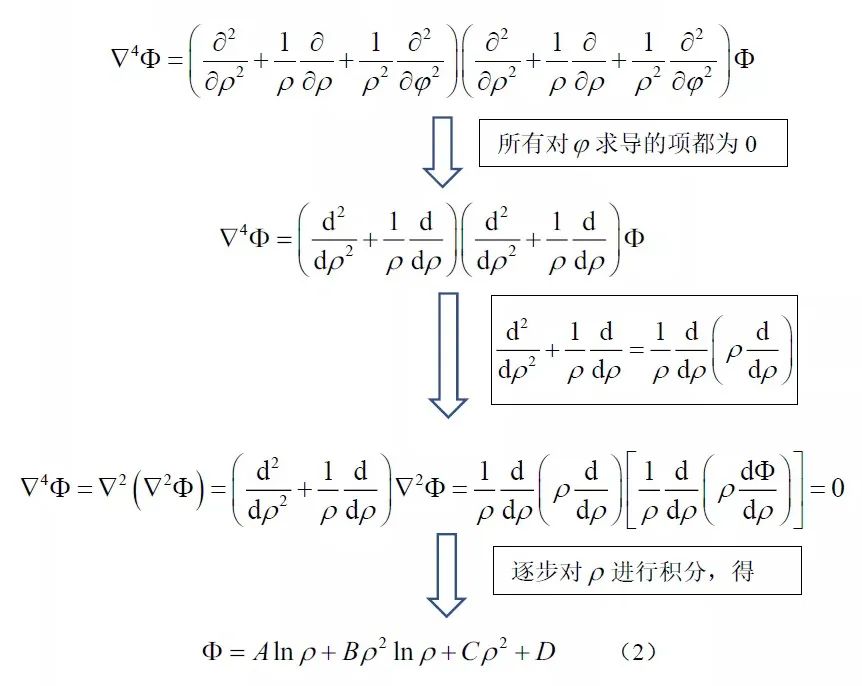
將其代入到應(yīng)力函數(shù)表達(dá)應(yīng)力分量的簡化公式，有

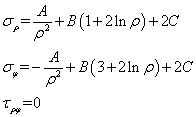
將上式代入物理方程（平面應(yīng)力問題）、幾何方程，可得位移解為

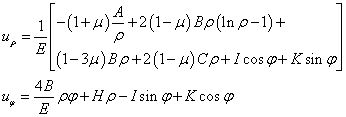
式中，含有常數(shù)H、I、K的項(xiàng)均為求解幾何方程時增加的項(xiàng)，代表剛體位移，如果只考慮形變位移時，可將其視為0。此外對于上式的第2式第一項(xiàng)(4B/E)ρφ，筒壁任意點(diǎn)的坐標(biāo)可表示為 (ρ, 2kπ+φ)，k為整數(shù)，也就是說極坐標(biāo)對一點(diǎn)的描述有周期性。然而，對于一點(diǎn)的環(huán)向位移uφ只能是一個值，這就是多連體必須要滿足的位移單值條件。為了滿足位移單值條件，只能有B=0。由此可見，

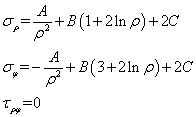
簡化為

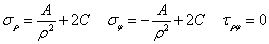
共有A和C兩個常數(shù)需要確定。考慮圓筒的邊界條件，在內(nèi)壁上

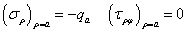
在圓筒外壁上，有

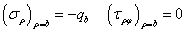
將應(yīng)力分量代入，可得

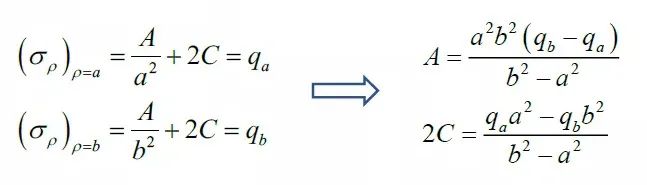
最后得，受均勻內(nèi)壓和外壓的圓筒應(yīng)力分布為

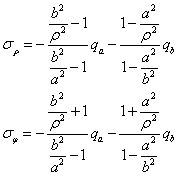
這就是拉梅-克拉貝隆解，利用該解我們可以推廣得出一系列的解，例如只有內(nèi)壓而無外壓的情況，只需令拉梅-克拉貝隆解中的qb=0；只有外壓而沒有內(nèi)壓時，只需令qa=0；若是無限大體中的圓筒只受內(nèi)壓，即qb=0且b>>a時，將上兩式分子、分母同除以b2，并忽略1/b2，得

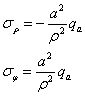
如果考慮位移邊界條件，這一問題還可以推廣為外壁固定有內(nèi)壓或內(nèi)壁固定有外壓，以及多層圓筒相套的接觸問題，拉梅-克拉貝隆解無疑為解決結(jié)構(gòu)中開圓孔問題奠定了重要的理論基礎(chǔ)。

1898年，德國工程師吉爾斯 (Ernst Gustav Kirsch, 1841-1901) 在德國第39屆工程學(xué)會一般會議上發(fā)表了他有關(guān)無限大體中含圓孔時孔口應(yīng)力分布的成果。他首先回顧了拉梅-克拉貝隆解，并將其推廣到無限大板開圓孔問題，但也指出了這種條件在實(shí)際工程中的有限性。從而，提出研究受載荷平板中含有圓孔的應(yīng)力分布問題的必要性。

圖3 吉爾斯和他的孔口應(yīng)力集中

如圖4所示，設(shè)有一平板，在其橫向受均勻載荷q，板中心含有一半徑為a的圓孔。特別注意，要求圓孔距離板的邊界很遠(yuǎn)，且孔的半徑遠(yuǎn)小于板的尺寸，此時就可以將其視為一無限大平板中含有小圓孔的問題。

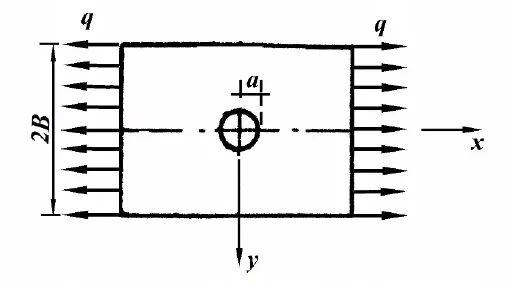
圖4 受橫向均勻載荷的平板含有圓孔問題

針對該問題，吉爾斯想到了絕妙的辦法，通過改造邊界條件，使這一問題轉(zhuǎn)化為可用拉梅-克拉貝隆解的方法。當(dāng)小圓孔遠(yuǎn)離邊界，且圓孔遠(yuǎn)小于板尺寸時，可圍繞圓孔再假定一個半徑為b的圓邊界，b遠(yuǎn)大于a，同時也遠(yuǎn)小于板尺寸，如圖5所示。

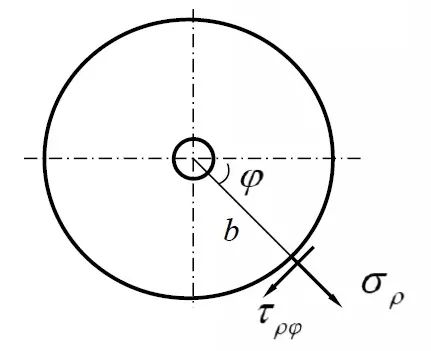
圖5 圍繞圓孔改造邊界條件

依據(jù)圖4所示的受力狀態(tài)，假想邊界上點(diǎn)的應(yīng)力狀態(tài)可表示為

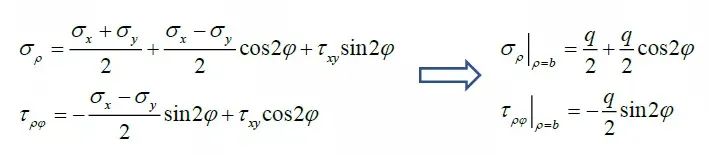
利用極坐標(biāo)和直角坐標(biāo)應(yīng)力分量變換公式，寫出假想邊界上極坐標(biāo)下的應(yīng)力分量，有

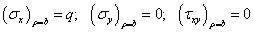
將其視為新邊界上的面力，無限大方平板含有小圓孔問題，就轉(zhuǎn)換成了無限大圓形板含有小圓孔問題，此時內(nèi)邊界條件可寫為

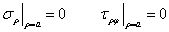
外邊界條件可寫為

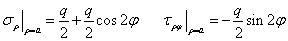
觀察外邊界條件，可分解為軸對稱和非軸對稱兩個部分，我們知道當(dāng)只考慮軸對稱部分時，就是拉梅-克拉貝隆解，為此，吉爾斯只需要集中精力求解非對稱部分，當(dāng)兩部分解分別得到后，疊加就可以得到最終的解。以下我們分別敘述。

問題一：考慮軸對稱邊界，如圖5所示圖形，只考慮外邊界的軸對稱部分，該問題可借用只有外壓而沒有內(nèi)壓的拉梅-克拉貝隆解，令受均勻內(nèi)壓和外壓的圓筒應(yīng)力分布公式中qa=0，qb=-q/2（負(fù)號表示拉應(yīng)力），并考慮b>>a，有

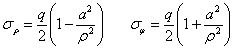
問題二：考慮非軸對稱邊界，觀察非軸對稱邊界條件，再依據(jù)極坐標(biāo)系下應(yīng)力分量與應(yīng)力函數(shù)的關(guān)系式，可假設(shè)σρ為ρ的某一函數(shù)，可設(shè)為f(ρ)，乘以cos2φ；τρφ為該函數(shù)乘以sin2φ。再依據(jù)應(yīng)力函數(shù)與應(yīng)力分量之間的關(guān)系

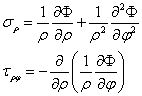
設(shè)出應(yīng)力函數(shù)為

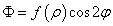
將其代入相容方程，有

在上式中，由于cos2φ不能總等于0，因此有

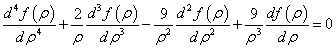
將上式兩邊同時乘以ρ4，上式轉(zhuǎn)變?yōu)闃?biāo)準(zhǔn)的歐拉方程，其求解過程如下

將f(ρ) 的表達(dá)式代回應(yīng)力函數(shù)，有

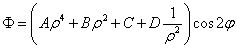
現(xiàn)在，我們將上述應(yīng)力函數(shù)代入應(yīng)力分量表達(dá)式，有

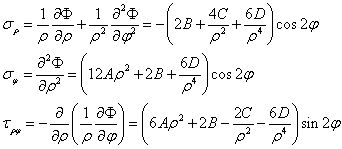
現(xiàn)在考慮邊界條件，內(nèi)邊界上有

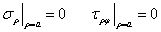
外邊界上，有

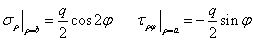
將應(yīng)力分量代入邊界條件，得

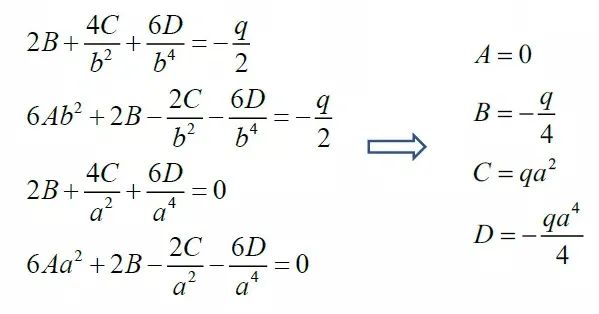
再將得到的常數(shù)代回應(yīng)力分量，有

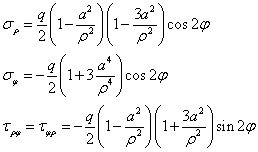
現(xiàn)在，我們已經(jīng)得到了軸對稱邊界和非軸對稱邊界下的應(yīng)力分布，主需要疊加上式和下式的結(jié)果

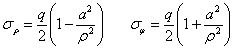
就可以得到完整的無限大平板開小圓孔的解答，如

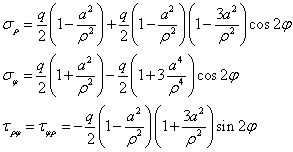
這就是無限大平板開圓孔的吉爾斯解答。由于圓孔開裂的控制應(yīng)力為σφ，顯然，孔邊隨角度變化的環(huán)向應(yīng)力σφ可寫為

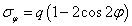
將q視為遠(yuǎn)端的均勻應(yīng)力，可見，當(dāng)φ=90°時，(1-2cos2φ) 取得最大值，為3。因此，圓孔周邊應(yīng)力最大為遠(yuǎn)端應(yīng)力的3倍。當(dāng)φ=0°時，環(huán)向應(yīng)力為-q，這也驗(yàn)證了泊松效應(yīng)，一個方向?yàn)槭芾瓡r，垂直方向上受壓。

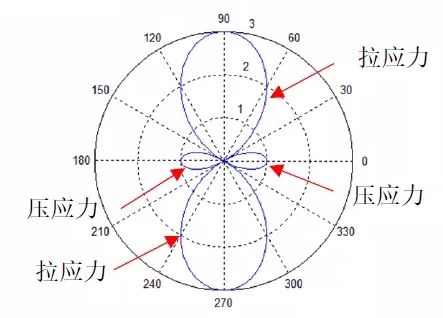
圖6 孔邊應(yīng)力分布情況

再來觀察圓孔周邊應(yīng)力集中的范圍，先假定φ=90°，寫出σφ的表達(dá)式為

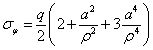
經(jīng)過簡單計(jì)算可以發(fā)現(xiàn)，當(dāng)ρ=a時，σφ取最大值，為3q；當(dāng)ρ=2a時，σφ=1.22q；當(dāng)ρ=3a時，σφ=1.07q；當(dāng)ρ=4a時，σφ=1.04q，可見在3倍半徑之后，孔邊應(yīng)力與遠(yuǎn)端均勻應(yīng)力就只有7%的差別了，并且距離圓孔越遠(yuǎn)就趨近于遠(yuǎn)端的均勻應(yīng)力，如圖7(a)所示。這也啟示我們，當(dāng)需要在結(jié)構(gòu)開多個孔時，孔間的距離至少要在3倍半徑之上，這樣可近似認(rèn)為兩孔之間沒有相互影響。

再假定φ=0°，寫出σφ的表達(dá)式為

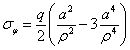
在沿著φ=0°的直線上，當(dāng)ρ=a時，σφ=-q；ρ=√3a時，σφ=0，隨后應(yīng)力迅速變?yōu)?，如圖7(b)所示。

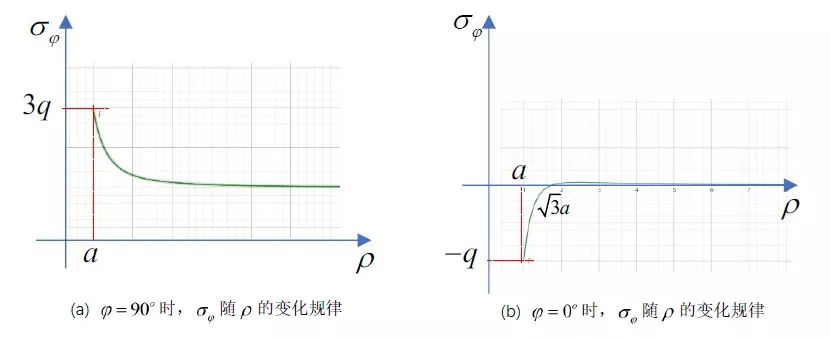
圖7 環(huán)向應(yīng)力隨離開圓孔的距離變化時的分布

如果稍關(guān)注一下拉梅-克拉貝隆、吉爾斯的背景就會發(fā)現(xiàn)，他們都有礦業(yè)工程背景，他們研究這一問題的動機(jī)很可能在于解決礦業(yè)工程中地下開挖時的力分布問題。不過很快，這一問題的解利用疊加原理被推廣到了多種場合下的應(yīng)用。例如，雙向受拉的問題分解成一個水平方向受拉和一個垂直方向受拉，兩個吉爾斯解。

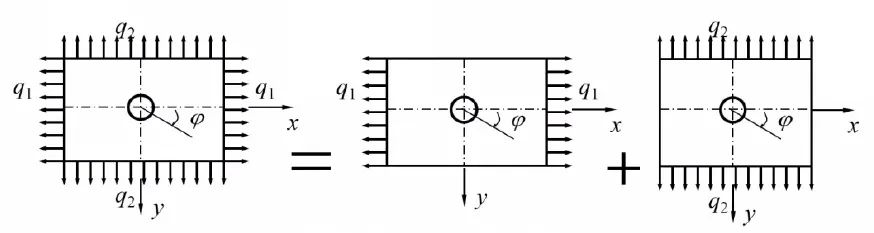
圖8 雙向受拉狀態(tài)下的開孔問題

純剪狀態(tài)下的開孔問題，通過應(yīng)力狀態(tài)等效，將其等效為一個方向受拉、另一個方向受壓的情況，如圖9所示。

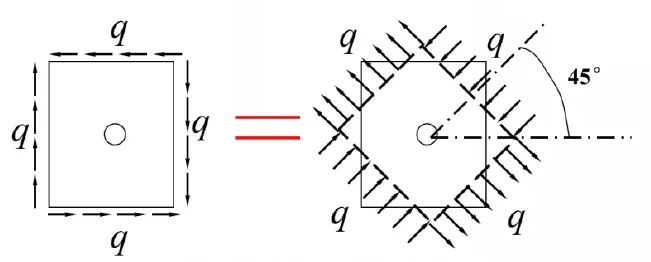
圖9 純剪狀態(tài)下開孔問題

還可以通過疊加，求出當(dāng)存在一群孔時結(jié)構(gòu)中的應(yīng)力分布。吉爾斯解的意義不僅在于為解決工程上的開孔問題提供了依據(jù)，也為另一門力學(xué)分支奠定了基礎(chǔ)。在吉爾斯解的基礎(chǔ)上，蘇聯(lián)科學(xué)家Kolosov(1909)、Inglish(1913)，以及Muskhelishvili (1953) 都得到了橢圓孔的應(yīng)力分布，Griffith(1921) 在Inglish 解的基礎(chǔ)上推導(dǎo)了含裂紋構(gòu)件的強(qiáng)度，奠定了斷裂力學(xué)的發(fā)展基礎(chǔ)。

編輯：黃飛