深入理解線段樹：線段樹的區(qū)間修改與懶惰標記
作者 | 京東云開發(fā)者-王奕龍
線段樹（Segment Tree）是常用的維護區(qū)間信息的數據結構，它可以在 O (logn) 的時間復雜度下實現單點修改、區(qū)間修改、區(qū)間查詢（區(qū)間求和、區(qū)間最大值或區(qū)間最小值）等操作，常用來解決 RMQ 問題。
RMQ (Range Minimum/Maximum Query) 問題是指：對于長度為 n 的數列 A，回答若干詢問 RMQ (A, i, j) 其中 i, j <= n，返回數列 A 中下標在 i, j 里的最小 (大）值。也就是說：RMQ 問題是指求區(qū)間最值的問題。通常該類型題目的解法有遞歸分治、動態(tài)規(guī)劃、線段樹和單調棧 / 單調隊列。
這篇內容斷斷續(xù)續(xù)寫了兩周，隨著練習對線段樹的理解不斷深入，慢慢地學習下來也不覺得它有多么困難，更多的體會還是熟能生巧，雖然它起初看上去確實代碼量大一些，但是我覺得只要大家放平心態(tài)，循序漸進的掌握下文中的三部分，也沒什么難的。
1. 線段樹
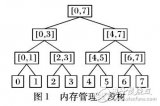
線段樹會將每個長度不為 1 的區(qū)間劃分成左右兩個區(qū)間來遞歸求解，通過合并左右兩區(qū)間的信息來求得當前區(qū)間的信息。 比如，我們將一個大小為 5 的數組 nums = {10, 11, 12, 13, 14} 轉換成線段樹，并規(guī)定線段樹的根節(jié)點編號為 1。用數組 tree [] 來保存線段樹的節(jié)點，tree [i] 表示線段樹上編號為 i 的節(jié)點，圖示如下：
圖示中每個節(jié)點展示了區(qū)間和以及區(qū)間范圍，tree [i] 左子樹節(jié)點為 tree [2i]，右子樹節(jié)點為 tree [2i + 1]。如果 tree [i] 記錄的區(qū)間為 [a, b] 的話，那么左子樹節(jié)點記錄的區(qū)間為 [a, mid]，右子樹節(jié)點記錄的區(qū)間為 [mid + 1, b]，其中 mid = (a + b) / 2。 現在我們已經對線段樹有了基本的認識，接下來我們看看區(qū)間查詢和單點修改的代碼實現。
區(qū)間查詢和單點修改線段樹
首先，我們定義線段樹的節(jié)點：
/**
* 定義線段樹節(jié)點
*/
class Node {
/**
* 區(qū)間和 或 區(qū)間最大/最小值
*/
int val;
int left;
int right;
public Node(int left, int right) {
this.left = left;
this.right = right;
}
}
注意其中的 val 字段保存的是區(qū)間的和。定義完樹的節(jié)點，我們來看一下建樹的邏輯，注意代碼中的注釋，我們?yōu)榫€段樹分配的節(jié)點數組大小為原數組大小的 4 倍，這是考慮到數組轉換成滿二叉樹的最壞情況。
public SegmentTree(int[] nums) {
this.nums = nums;
tree = new Node[nums.length * 4];
// 建樹，注意表示區(qū)間時使用的是從 1 開始的索引值
build(1, 1, nums.length);
}
/**
* 建樹
*
* @param pos 當前節(jié)點編號
* @param left 當前節(jié)點區(qū)間下界
* @param right 當前節(jié)點區(qū)間上界
*/
private void build(int pos, int left, int right) {
// 創(chuàng)建節(jié)點
tree[pos] = new Node(left, right);
// 遞歸結束條件
if (left == right) {
// 賦值
tree[pos].val = nums[left - 1];
return;
}
// 如果沒有到根節(jié)點，則繼續(xù)遞歸
int mid = left + right >> 1;
build(pos << 1, left, mid);
build(pos << 1 | 1, mid + 1, right);
// 當前節(jié)點的值是左子樹和右子樹節(jié)點的和
pushUp(pos);
}
/**
* 用于向上回溯時修改父節(jié)點的值
*/
private void pushUp(int pos) {
tree[pos].val = tree[pos << 1].val + tree[pos << 1 | 1].val;
}我們在建樹時，表示區(qū)間并不是從索引 0 開始，而是從索引 1 開始，這樣才能保證在計算左子樹節(jié)點索引時為 2i，右子樹節(jié)點索引為 2i + 1。 build()方法執(zhí)行時，我們會先在對應的位置上創(chuàng)建節(jié)點而不進行賦值，只有在遞歸到葉子節(jié)點時才賦值，此時區(qū)間大小為 1，節(jié)點值即為當前區(qū)間的值。之后非葉子節(jié)點值都是通過pushUp()方法回溯加和當前節(jié)點的兩個子節(jié)點值得出來的。 接下來我們看修改區(qū)間中的值，線段樹對值的更新方法，關注其中的注釋：
/**
* 修改單節(jié)點的值
*
* @param pos 當前節(jié)點編號
* @param numPos 需要修改的區(qū)間中值的位置
* @param val 修改后的值
*/
private void update(int pos, int numPos, int val) {
// 找到該數值所在線段樹中的葉子節(jié)點
if (tree[pos].left == numPos && tree[pos].right == numPos) {
tree[pos].val = val;
return;
}
// 如果不是當前節(jié)點那么需要判斷是去左或右去找
int mid = tree[pos].left + tree[pos].right >> 1;
if (numPos <= mid) {
update(pos << 1, numPos, val);
} else {
update(pos << 1 | 1, numPos, val);
}
// 葉子節(jié)點的值修改完了，需要回溯更新所有相關父節(jié)點的值
pushUp(pos);
}
修改方法比較簡單，當葉子節(jié)點值更新完畢時，我們仍然需要調用pushUp()方法對所有相關父節(jié)點值進行更新。 接下來我們看查找對應區(qū)間和的方法：
/**
* 查找對應區(qū)間的值
*
* @param pos 當前節(jié)點
* @param left 要查詢的區(qū)間的下界
* @param right 要查詢的區(qū)間的上界
*/
private int query(int pos, int left, int right) {
// 如果我們要查找的區(qū)間把當前節(jié)點區(qū)間全部包含起來
if (left <= tree[pos].left && tree[pos].right <= right) {
return tree[pos].val;
}
int res = 0;
int mid = tree[pos].left + tree[pos].right >> 1;
// 根據區(qū)間范圍去左右節(jié)點分別查找求和
if (left <= mid) {
res += query(pos << 1, left, right);
}
if (right > mid) {
res += query(pos << 1 | 1, left, right);
}
return res;
}
該方法也比較簡單，需要判斷區(qū)間范圍是否需要對向左子節(jié)點和右子節(jié)點的分別查找計算。 現在表示區(qū)間和的線段樹已經講解完畢了，為了方便大家學習和看代碼，我把全量的代碼在這里貼出來：
public class SegmentTree {
/**
* 定義線段樹節(jié)點
*/
static class Node {
/**
* 區(qū)間和 或 區(qū)間最大/最小值
*/
int val;
int left;
int right;
public Node(int left, int right) {
this.left = left;
this.right = right;
}
}
Node[] tree;
int[] nums;
public SegmentTree(int[] nums) {
this.nums = nums;
tree = new Node[nums.length * 4];
// 建樹，注意表示區(qū)間時使用的是從 1 開始的索引值
build(1, 1, nums.length);
}
/**
* 建樹
*
* @param pos 當前節(jié)點編號
* @param left 當前節(jié)點區(qū)間下界
* @param right 當前節(jié)點區(qū)間上界
*/
private void build(int pos, int left, int right) {
// 創(chuàng)建節(jié)點
tree[pos] = new Node(left, right);
// 遞歸結束條件
if (left == right) {
// 賦值
tree[pos].val = nums[left - 1];
return;
}
// 如果沒有到根節(jié)點，則繼續(xù)遞歸
int mid = left + right >> 1;
build(pos << 1, left, mid);
build(pos << 1 | 1, mid + 1, right);
// 當前節(jié)點的值是左子樹和右子樹節(jié)點的和
pushUp(pos);
}
/**
* 修改單節(jié)點的值
*
* @param pos 當前節(jié)點編號
* @param numPos 需要修改的區(qū)間中值的位置
* @param val 修改后的值
*/
private void update(int pos, int numPos, int val) {
// 找到該數值所在線段樹種的葉子節(jié)點
if (tree[pos].left == numPos && tree[pos].right == numPos) {
tree[pos].val = val;
return;
}
// 如果不是當前節(jié)點那么需要判斷是去左或右去找
int mid = tree[pos].left + tree[pos].right >> 1;
if (numPos <= mid) {
update(pos << 1, numPos, val);
} else {
update(pos << 1 | 1, numPos, val);
}
// 葉子節(jié)點的值修改完了，需要回溯更新所有相關父節(jié)點的值
pushUp(pos);
}
/**
* 用于向上回溯時修改父節(jié)點的值
*/
private void pushUp(int pos) {
tree[pos].val = tree[pos << 1].val + tree[pos << 1 | 1].val;
}
/**
* 查找對應區(qū)間的值
*
* @param pos 當前節(jié)點
* @param left 要查詢的區(qū)間的下界
* @param right 要查詢的區(qū)間的上界
*/
private int query(int pos, int left, int right) {
// 如果我們要查找的區(qū)間把當前節(jié)點區(qū)間全部包含起來
if (left <= tree[pos].left && tree[pos].right <= right) {
return tree[pos].val;
}
int res = 0;
int mid = tree[pos].left + tree[pos].right >> 1;
// 根據區(qū)間范圍去左右節(jié)點分別查找求和
if (left <= mid) {
res += query(pos << 1, left, right);
}
if (right > mid) {
res += query(pos << 1 | 1, left, right);
}
return res;
}
}
如果要創(chuàng)建表示區(qū)間最大值或最小值的線段樹，建樹的邏輯不變，只需要將 **pushUp ()方法和query ()** 方法修改成計算最大值或最小值的邏輯即可。
2. 線段樹的區(qū)間修改與懶惰標記
如果我們不僅對單點進行修改，也對區(qū)間進行修改，那么在區(qū)間修改時就需要將當前區(qū)間值及包含當前區(qū)間的子區(qū)間值都修改一遍，這樣所產生的開銷是沒辦法接受的，因此在這里我們會使用一種懶惰標記的方法來幫助我們避免這種即時開銷。 簡單來說，懶惰標記是通過延遲對節(jié)點信息的更改，從而減少可能不必要的操作次數。每次執(zhí)行修改時，我們通過打標記的方法表明該節(jié)點對應的區(qū)間在某一次操作中被更改，但不更新該節(jié)點的子節(jié)點的信息。實質性的修改則在下一次 **“即將訪問（update 或 query）” 到帶有懶惰標記節(jié)點的子節(jié)點 ** 時才進行。 我們通過在節(jié)點類中添加 add 字段記錄懶惰標記，它表示的是該區(qū)間的子區(qū)間值需要 “變化的大小”（一定好好好的理解），并通過 pushDown 方法 “累加” 到當前區(qū)間的兩個子節(jié)點區(qū)間值中。
只要不訪問到當前區(qū)間的子區(qū)間，那么子區(qū)間值始終都不會變化，相當于子區(qū)間值的變化量被當前節(jié)點通過 add 字段 “持有”
pushDown 方法區(qū)別于我們上文中提到的 pushUp 方法，前者是將當前節(jié)點值累計的懶惰標記值同步到子節(jié)點中，而后者是完成子節(jié)點修改后，回溯修改當前子節(jié)點的父節(jié)點值，我們能夠根據 Down 和 Up 來更好的理解這兩個方法的作用方向和修改范圍。 下面我們一起來看看過程和具體的代碼，節(jié)點類如下，增加 add 字段：
static class Node {
int left;
int right;
int val;
int add;
public Node(int left, int right) {
this.left = left;
this.right = right;
}
}
區(qū)間修改
建樹的流程與我們上述的一致，就不在這里贅述了，我們主要關注區(qū)間修改的過程，還是以如下初始的線段樹為例，此時各個節(jié)點的 add 均為 0：
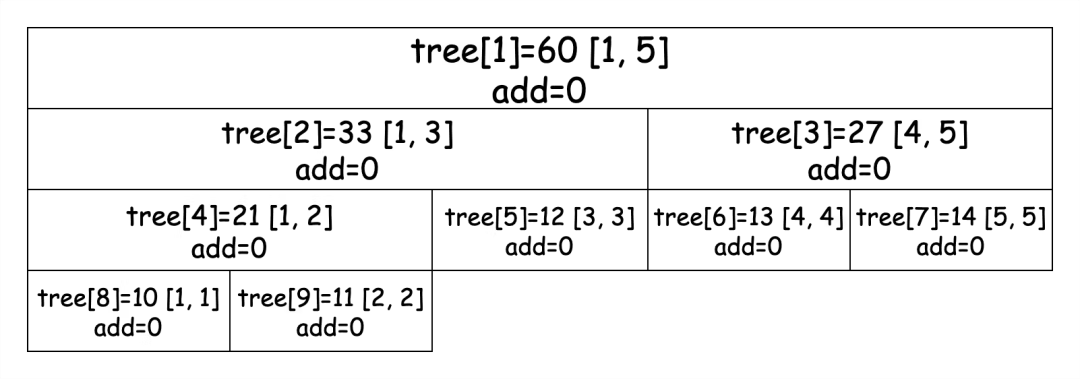
接下來我們修改區(qū)間 [3, 5] 且區(qū)間內每個值變化量為 1，過程如下： 先遍歷節(jié)點 1，發(fā)現 [3, 5] 區(qū)間不能將 [1, 5] 區(qū)間完全包含，不進行修改，繼續(xù)遍歷節(jié)點 2。節(jié)點 2 依然沒有被區(qū)間 [3, 5] 包含，需要繼續(xù)遍歷節(jié)點 5，發(fā)現該節(jié)點被區(qū)間完全包含，進行修改并添加懶惰標記值，如下圖所示：
完成這一步驟后需要向上回溯修改 tree [2] 節(jié)點的值：
現在 [3, 5] 區(qū)間中 3 已經完成修改，還有 4, 5 沒有被修改，我們需要在右子樹中繼續(xù)遞歸查找，發(fā)現 tree [3] 中區(qū)間被我們要修改的區(qū)間 [3, 5] 完全包含，那么需要將這個節(jié)點進行修改并懶惰標記，如下，注意這里雖然 tree [3] 節(jié)點有兩個子節(jié)點，但是因為我們沒有訪問到它的子節(jié)點所以無需同步 add 值到各個子節(jié)點中：
同樣，完成這一步驟也需要向上回溯修改父節(jié)點的值：
到現在我們的區(qū)間修改就已經完成了，根據這個過程代碼示例如下：
/**
* 修改區(qū)間的值
*
* @param pos 當前節(jié)點編號
* @param left 要修改區(qū)間的下界
* @param right 要修改區(qū)間的上界
* @param val 區(qū)間內每個值的變化量
*/
public void update(int pos, int left, int right, int val) {
// 如果該區(qū)間被要修改的區(qū)間包圍的話，那么需要將該區(qū)間所有的值都修改
if (left <= tree[pos].left && tree[pos].right <= right) {
tree[pos].val += (tree[pos].right - tree[pos].left + 1) * val;
// 懶惰標記
tree[pos].add += val;
return;
}
// 該區(qū)間沒有被包圍的話，需要修改節(jié)點的信息
pushDown(pos);
int mid = tree[pos].left + tree[pos].right >> 1;
// 如果下界在 mid 左邊，那么左子樹需要修改
if (left <= mid) {
update(pos << 1, left, right, val);
}
// 如果上界在 mid 右邊，那么右子樹也需要修改
if (right > mid) {
update(pos << 1 | 1, left, right, val);
}
// 修改完成后向上回溯修改父節(jié)點的值
pushUp(pos);
}
private void pushDown(int pos) {
// 根節(jié)點 和 懶惰標記為 0 的情況不需要再向下遍歷
if (tree[pos].left != tree[pos].right && tree[pos].add != 0) {
int add = tree[pos].add;
// 計算累加變化量
tree[pos << 1].val += add * (tree[pos << 1].right - tree[pos << 1].left + 1);
tree[pos << 1 | 1].val += add * (tree[pos << 1 | 1].right - tree[pos << 1 | 1].left + 1);
// 子節(jié)點懶惰標記累加
tree[pos << 1].add += add;
tree[pos << 1 | 1].add += add;
// 懶惰標記清 0
tree[pos].add = 0;
}
}
private void pushUp(int pos) {
tree[pos].val = tree[pos << 1].val + tree[pos << 1 | 1].val;
}
區(qū)間查詢
tree [3] 節(jié)點是有懶惰標記 1 的，如果我們此時查詢區(qū)間 [5, 5] 的值，就需要在遞歸經過 tree [3] 節(jié)點時，進行 pushDown 懶惰標記計算，將 tree [6] 和 tree [7] 的節(jié)點值進行修改，結果如下：
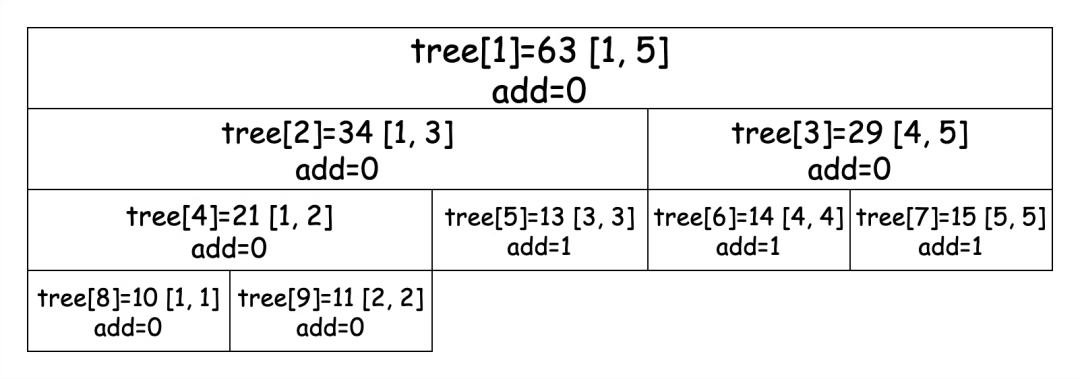
最終我們會獲取到結果值為 15，區(qū)間查詢過程的示例代碼如下：
public int query(int pos, int left, int right) {
if (left <= tree[pos].left && tree[pos].right <= right) {
// 當前區(qū)間被包圍
return tree[pos].val;
}
// 懶惰標記需要下傳修改子節(jié)點的值
pushDown(pos);
int res = 0;
int mid = tree[pos].left + tree[pos].right >> 1;
if (left <= mid) {
res += query(pos << 1, left, right);
}
if (right > mid) {
res += query(pos << 1 | 1, left, right);
}
return res;
}
同樣，為了方便大家學習，我把全量代碼也列出來，我認為學習線段樹的區(qū)間修改比較重要的點是理解 add 字段表示的含義和 pushDown 方法的作用時機，而且需要注意只有線段樹中的某個區(qū)間被我們要修改的區(qū)間全部包含時（update 和 query 方法的條件判斷），才進行值修改并懶惰標記，否則該區(qū)間值只在 pushUp 方法回溯時被修改。
public class SegmentTree2 {
static class Node {
int left;
int right;
int val;
int add;
public Node(int left, int right) {
this.left = left;
this.right = right;
}
}
Node[] tree;
int[] nums;
public SegmentTree2(int[] nums) {
this.tree = new Node[nums.length * 4];
this.nums = nums;
build(1, 1, nums.length);
}
private void build(int pos, int left, int right) {
tree[pos] = new Node(left, right);
// 遞歸結束條件
if (left == right) {
tree[pos].val = nums[left - 1];
return;
}
int mid = left + right >> 1;
build(pos << 1, left, mid);
build(pos << 1 | 1, mid + 1, right);
// 回溯修改父節(jié)點的值
pushUp(pos);
}
/**
* 修改區(qū)間的值
*
* @param pos 當前節(jié)點編號
* @param left 要修改區(qū)間的下界
* @param right 要修改區(qū)間的上界
* @param val 區(qū)間內每個值的變化量
*/
public void update(int pos, int left, int right, int val) {
// 如果該區(qū)間被要修改的區(qū)間包圍的話，那么需要將該區(qū)間所有的值都修改
if (left <= tree[pos].left && tree[pos].right <= right) {
tree[pos].val += (tree[pos].right - tree[pos].left + 1) * val;
// 懶惰標記
tree[pos].add += val;
return;
}
// 該區(qū)間沒有被包圍的話，需要修改節(jié)點的信息
pushDown(pos);
int mid = tree[pos].left + tree[pos].right >> 1;
// 如果下界在 mid 左邊，那么左子樹需要修改
if (left <= mid) {
update(pos << 1, left, right, val);
}
// 如果上界在 mid 右邊，那么右子樹也需要修改
if (right > mid) {
update(pos << 1 | 1, left, right, val);
}
// 修改完成后向上回溯修改父節(jié)點的值
pushUp(pos);
}
public int query(int pos, int left, int right) {
if (left <= tree[pos].left && tree[pos].right <= right) {
// 當前區(qū)間被包圍
return tree[pos].val;
}
// 懶惰標記需要下傳修改子節(jié)點的值
pushDown(pos);
int res = 0;
int mid = tree[pos].left + tree[pos].right >> 1;
if (left <= mid) {
res += query(pos << 1, left, right);
}
if (right > mid) {
res += query(pos << 1 | 1, left, right);
}
return res;
}
private void pushDown(int pos) {
// 根節(jié)點 和 懶惰標記為 0 的情況不需要再向下遍歷
if (tree[pos].left != tree[pos].right && tree[pos].add != 0) {
int add = tree[pos].add;
// 計算累加變化量
tree[pos << 1].val += add * (tree[pos << 1].right - tree[pos << 1].left + 1);
tree[pos << 1 | 1].val += add * (tree[pos << 1 | 1].right - tree[pos << 1 | 1].left + 1);
// 子節(jié)點懶惰標記
tree[pos << 1].add += add;
tree[pos << 1 | 1].add += add;
// 懶惰標記清 0
tree[pos].add = 0;
}
}
private void pushUp(int pos) {
tree[pos].val = tree[pos << 1].val + tree[pos << 1 | 1].val;
}
}
3. 線段樹動態(tài)開點
線段樹的動態(tài)開點其實不難理解，它與我們上述直接創(chuàng)建好線段樹所有節(jié)點不同，動態(tài)開點的線段樹在最初只創(chuàng)建一個根節(jié)點代表整個區(qū)間，其他節(jié)點只在需要的時候被創(chuàng)建，節(jié)省出了空間。當然，我們因此也不能再使用pos << 1?和?pos << 1 | 1?來尋找當前節(jié)點的左右子節(jié)點，取而代之的是在節(jié)點中使用 left 和 right 記錄左右子節(jié)點在 tree [] 中的位置，這一點需要注意：
static class Node {
// left 和 right 不再表示區(qū)間范圍而是表示左右子節(jié)點在 tree 中的索引位置
int left, right;
int val;
int add;
}
我們以區(qū)間 [1, 5] 為例，創(chuàng)建區(qū)間 [5, 5] 為 14 的過程圖示如下：
/**
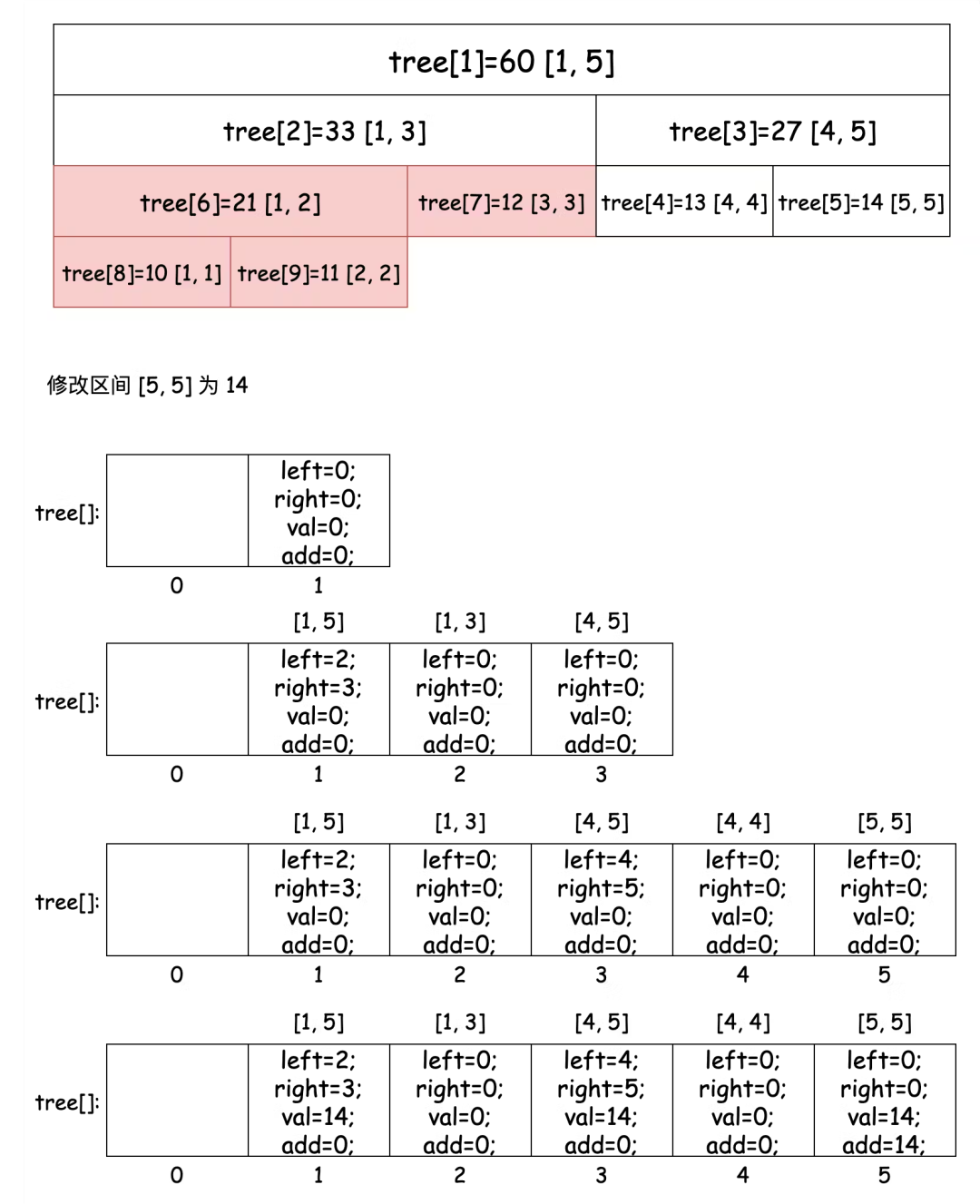
* 修改區(qū)間的值
*
* @param pos 當前節(jié)點的索引值
* @param left 當前線段樹節(jié)點表示的范圍下界
* @param right 當前線段樹節(jié)點表示的范圍上界
* @param l 要修改的區(qū)間下界
* @param r 要修改的區(qū)間上界
* @param val 區(qū)間值變化的大小
*/
public void update(int pos, int left, int right, int l, int r, int val) {
// 當前區(qū)間被要修改的區(qū)間全部包含
if (l <= left && right <= r) {
tree[pos].val += (right - left + 1) * val;
tree[pos].add += val;
return;
}
lazyCreate(pos);
pushDown(pos, right - left + 1);
int mid = left + right >> 1;
if (l <= mid) {
update(tree[pos].left, left, mid, l, r, val);
}
if (r > mid) {
update(tree[pos].right, mid + 1, right, l, r, val);
}
pushUp(pos);
}
// 為該位置創(chuàng)建節(jié)點
private void lazyCreate(int pos) {
if (tree[pos] == null) {
tree[pos] = new Node();
}
// 創(chuàng)建左子樹節(jié)點
if (tree[pos].left == 0) {
tree[pos].left = ++count;
tree[tree[pos].left] = new Node();
}
// 創(chuàng)建右子樹節(jié)點
if (tree[pos].right == 0) {
tree[pos].right = ++count;
tree[tree[pos].right] = new Node();
}
}
private void pushDown(int pos, int len) {
if (tree[pos].left != 0 && tree[pos].right != 0 && tree[pos].add != 0) {
// 計算左右子樹的值
tree[tree[pos].left].val += (len - len / 2) * tree[pos].add;
tree[tree[pos].right].val += len / 2 * tree[pos].add;
// 子節(jié)點懶惰標記
tree[tree[pos].left].add += tree[pos].add;
tree[tree[pos].right].add += tree[pos].add;
tree[pos].add = 0;
}
}
private void pushUp(int pos) {
tree[pos].val = tree[tree[pos].left].val + tree[tree[pos].right].val;
}
整體的邏輯并不難，新增的 lazyCreate 方法是動態(tài)開點的邏輯，需要注意的是執(zhí)行區(qū)間更新時我們方法的參數中多了 left 和 right 表示當前節(jié)點區(qū)間范圍的參數，因為我們現在的節(jié)點中只保存了左右子節(jié)點的位置，而沒有區(qū)間信息，所以我們需要在參數中攜帶才行，否則我們沒有辦法判斷當前區(qū)間和要找的區(qū)間是否匹配。 我還是將全量代碼放在下面，方便大家學習：
public class SegmentTree3 {
static class Node {
// left 和 right 不再表示區(qū)間范圍而是表示左右子節(jié)點在 tree 中的索引位置
int left, right;
int val;
int add;
}
// 記錄當前節(jié)點數
int count;
Node[] tree;
public SegmentTree3() {
count = 1;
tree = new Node[(int) 5e6];
tree[count] = new Node();
}
public int query(int pos, int left, int right, int l, int r) {
if (l <= left && right <= r) {
return tree[pos].val;
}
lazyCreate(pos);
pushDown(pos, right - left + 1);
int res = 0;
int mid = left + right >> 1;
if (l <= mid) {
res += query(tree[pos].left, left, mid, l, r);
}
if (r > mid) {
res += query(tree[pos].right, mid + 1, right, l, r);
}
return res;
}
/**
* 修改區(qū)間的值
*
* @param pos 當前節(jié)點的索引值
* @param left 當前線段樹節(jié)點表示的范圍下界
* @param right 當前線段樹節(jié)點表示的范圍上界
* @param l 要修改的區(qū)間下界
* @param r 要修改的區(qū)間上界
* @param val 區(qū)間值變化的大小
*/
public void update(int pos, int left, int right, int l, int r, int val) {
// 當前區(qū)間被要修改的區(qū)間全部包含
if (l <= left && right <= r) {
tree[pos].val += (right - left + 1) * val;
tree[pos].add += val;
return;
}
lazyCreate(pos);
pushDown(pos, right - left + 1);
int mid = left + right >> 1;
if (l <= mid) {
update(tree[pos].left, left, mid, l, r, val);
}
if (r > mid) {
update(tree[pos].right, mid + 1, right, l, r, val);
}
pushUp(pos);
}
// 為該位置創(chuàng)建節(jié)點
private void lazyCreate(int pos) {
if (tree[pos] == null) {
tree[pos] = new Node();
}
// 創(chuàng)建左子樹節(jié)點
if (tree[pos].left == 0) {
tree[pos].left = ++count;
tree[tree[pos].left] = new Node();
}
// 創(chuàng)建右子樹節(jié)點
if (tree[pos].right == 0) {
tree[pos].right = ++count;
tree[tree[pos].right] = new Node();
}
}
private void pushDown(int pos, int len) {
if (tree[pos].left != 0 && tree[pos].right != 0 && tree[pos].add != 0) {
// 計算左右子樹的值
tree[tree[pos].left].val += (len - len / 2) * tree[pos].add;
tree[tree[pos].right].val += len / 2 * tree[pos].add;
// 子節(jié)點懶惰標記
tree[tree[pos].left].add += tree[pos].add;
tree[tree[pos].right].add += tree[pos].add;
tree[pos].add = 0;
}
}
private void pushUp(int pos) {
tree[pos].val = tree[tree[pos].left].val + tree[tree[pos].right].val;
}
}
編輯：黃飛
聲明：本文內容及配圖由入駐作者撰寫或者入駐合作網站授權轉載。文章觀點僅代表作者本人，不代表電子發(fā)燒友網立場。文章及其配圖僅供工程師學習之用，如有內容侵權或者其他違規(guī)問題，請聯系本站處理。
舉報投訴
-
編程
+關注
關注
88文章
3640瀏覽量
94031 -
代碼
+關注
關注
30文章
4837瀏覽量
69121
原文標題：深入理解線段樹
文章出處：【微信號：OSC開源社區(qū)，微信公眾號：OSC開源社區(qū)】歡迎添加關注！文章轉載請注明出處。
發(fā)布評論請先 登錄
相關推薦
深入理解和實現RTOS_連載
和trcohili的帖子。trochili rtos完全是作者興趣所在，且行且堅持，比沒有duo。深入理解和實現RTOS_連載1_RTOS的前生今世今天發(fā)布的是第一篇，"RTOS的前生今世"
發(fā)表于 05-30 01:02
CAD怎么連接線段？CAD線段連接教程
在CAD繪圖過程中，如果想要連接兩條線段的話該如何操作呢？其實很簡答，接下來的CAD教程就和小編一起來了解一下浩辰CAD建筑軟件中CAD線段連接的相關操作技巧吧！CAD連接線段的操作步驟：浩辰CAD
發(fā)表于 06-06 20:33
對棧的深入理解
為什么要深入理解棧？做C語言開發(fā)如果棧設置不合理或者使用不對，棧就會溢出，溢出就會遇到無法預測亂飛現象。所以對棧的深入理解是非常重要的。注：動畫如果看不清楚可以電腦看更清晰啥是棧先來看一段動畫：沒有
發(fā)表于 02-15 07:01
為什么要深入理解棧
[導讀] 從這篇文章開始，將會不定期更新關于嵌入式C語言編程相關的個人認為比較重要的知識點，或者踩過的坑。為什么要深入理解棧？做C語言開發(fā)如果棧設置不合理或者使用不對，棧就會溢出，溢出就會遇到無法
發(fā)表于 02-15 06:09
基于幾何約束的視頻幀間線段特征匹配算法
針對線段因遮擋、斷裂以及端點提取不準確等原因造成的線段特征匹配困難問題，特別是現有匹配算法在匹配過程中出現多配多時直接采取最相似匹配而導致丟失大量真實匹配的問題，提出了一種基于多重幾何約束及0-1
發(fā)表于 11-29 10:20
?0次下載
基于線段樹的內存管理方法
現有的內存管理的工作多集中在內存分配的效率上，實時性較好，但易產生內存碎片。為此，提出基于線段樹的高效內存管理方法。該方法將內存地址空間劃分為內存段，建立內存管理線段樹，基于所建立的內
發(fā)表于 12-27 14:06
?2次下載
一種比線段樹還高效的區(qū)間算法
但這里有個很明顯的問題，就是我們的數組f[i,j]定義的不合理，因為里面很多的小區(qū)間沒有用上，比如長度為3，5，6，7等，所以需要重新定義。
手動版實現帶箭頭的線段繪制
我根據一個矩形進行了各種角度旋轉，就想通過繪制一個帶方向的線段表示它，通過旋轉矩陣很容易的獲取了兩個點坐標，但是很快遇到了一個新問題，怎么繪制那個箭頭，就是帶箭頭的線段，OpenCV中的cv.line函數只支持繪制不帶箭頭的線段
工商網監(jiān)
評論