機器人在執(zhí)行期望目標任務時,我們希望機器人能精確地達到人類所預設的目標,那么我們就來理解下什么是最優(yōu)控制和逆最優(yōu)控制。
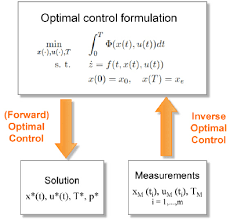
因此,最優(yōu)控制是期望最小化或者最大化目標。
很顯然最優(yōu)控制和逆最優(yōu)控制是一種相反的關系:
最優(yōu)控制理論是數(shù)學優(yōu)化的一個分支,它處理在一段時間內(nèi)為一個動態(tài)系統(tǒng)找到一個控制,使目標函數(shù)得到優(yōu)化。目標是找到目標控制律,使得優(yōu)化目標函數(shù)。
而逆最優(yōu)控制作為將生物運動傳遞給機器人的有前途的方法。逆最優(yōu)控制有助于(a)理解和識別基于測量的生物運動的潛在最優(yōu)標準,以及(b)建立可用于控制機器人運動的最優(yōu)控制模型。
逆最優(yōu)控制問題的目的是確定——對于給定的動態(tài)過程和觀察到的解——產(chǎn)生解的優(yōu)化準則。從數(shù)學的角度來看,逆最優(yōu)控制問題是困難的,因為它們需要解決最優(yōu)控制問題中的參數(shù)識別問題。
在最優(yōu)控制中,總的來看,其本質(zhì)就是讓系統(tǒng)以某種最小的代價來讓系統(tǒng)運行,當這個代價被定義為二次泛函,且系統(tǒng)是線性的話,那么這個問題就稱為線性二次問題,設計的控制器(即問題的解)可以稱為LQR(Linear Quadratic Regulator)線性二次調(diào)節(jié)器。
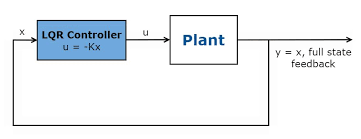
若被動系統(tǒng)是線性化表示,成本函數(shù)描述為二次泛函,那么這種問題就可以被認為是線性二次問題,求解此問題,即可以成為LQR問題!
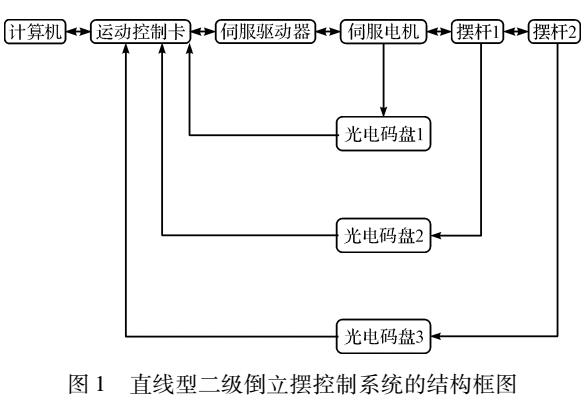
常見的模型為倒立擺模型:
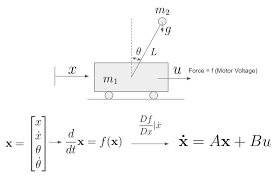
尋找模型的最佳參數(shù)的問題被轉(zhuǎn)化為一個 LQR 問題,該問題最大限度地減少了人力并優(yōu)化了閉環(huán)行為。
LQR 控制器的系統(tǒng)具有良好的穩(wěn)定性,并且在某個性能指標方面是最佳的。然而,當系統(tǒng)高度不確定時,LQR 控制不能保證魯棒穩(wěn)定性。
-
控制器
+關注
關注
114文章
17013瀏覽量
183230 -
機器人
+關注
關注
213文章
29551瀏覽量
211874 -
調(diào)節(jié)器
+關注
關注
5文章
876瀏覽量
47436
發(fā)布評論請先 登錄
主動隊列管理建模及最優(yōu)控制策略
0038《最優(yōu)控制理論》科學出版社-2003.pdf(5M)
主動隊列管理建模及最優(yōu)控制策略
大純滯后對象的最優(yōu)控制
狀態(tài)時滯系統(tǒng)的輸入多采樣最優(yōu)控制
最優(yōu)控制在直流調(diào)速系統(tǒng)中的應用
基于Legendre偽譜法的空間機器人姿態(tài)運動的最優(yōu)控制
直線二級倒立擺系統(tǒng)的H∞魯棒最優(yōu)控制
LQR控制算法之最優(yōu)控制
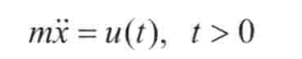





 什么是機器人最優(yōu)控制和逆最優(yōu)控制
什么是機器人最優(yōu)控制和逆最優(yōu)控制










評論