這篇是 ICLR 上用 TCN 來做一般的時間序列分析的論文,在 Rebuttal 之后的分數為 888,算得上是時間序列領域相關的論文中最高分那一檔了。本文提出了一個 ModernTCN 的模型,實現起來也很簡單,所以我后面附上了模型的代碼實現。

論文標題:
ModernTCN: A Modern Pure Convolution Structure for General Time Series Analysis
論文鏈接:
https://openreview.net/forum?id=vpJMJerXHU

Key Point
1.1 Motivation
作者發現,在時間序列領域,最近基于 TCN/CNN 的模型效果沒有基于Transformer 或 MLP 的模型效果好,而一些現代的 CNN 比如 ConvNeXt、SLaK 的性能都超過了 Vision Transformer。因此,作者想探究卷積是不是可以在時間序列分析領域獲得更好的性能。為此,有兩點可以改善 TCN 模型的地方。
首先是要提升感受野。在 CV 領域,現代卷積都有著很大的卷積核。作者發現在時間序列領域差不多,可以看下圖:

SCINet 和 MICN 是兩個基于 TCN 的預測模型,它們的感受野都很小。作者發現 ModernTCN 中采用大的卷積核所對應的感受野要大很多。
其次是充分利用卷積可以捕獲跨變量依賴性,也就是多變量時間序列中變量之間的關系。在 PatchTST 等最近的時間序列預測文章中,很多方法采用了通道獨立策略,這種策略直接將多變量序列預測中變量之間關系忽略了,反而取得了更好的效果。作者認為,變量之間關系仍然重要,但是要精心設計模型結構來捕獲。
1.2 從CV中汲取靈感(現代卷積結構)
在 CV 中,很多人發現 Transformer 之所以成功,可能是因為架構比較好。比如下圖左側,self-attention 負責 token 之間的混合,FFN 負責通道之間的混合,兩者分離開。同樣的,把混合 token 的結構替換為深度分離卷積(depth-wise 卷積,DWConv),把 FFN 換為完全等價的 ConvFFN(由兩個 point-wise Conv 加 GeLU 激活組成)。
不熟悉 depth-wise 卷積的可以去了解一下,它其實就是對每個通道采用獨立的核,這樣就不會混合通道,只會混合 token,大卷積核來獲取大感受野也是在這里用的。
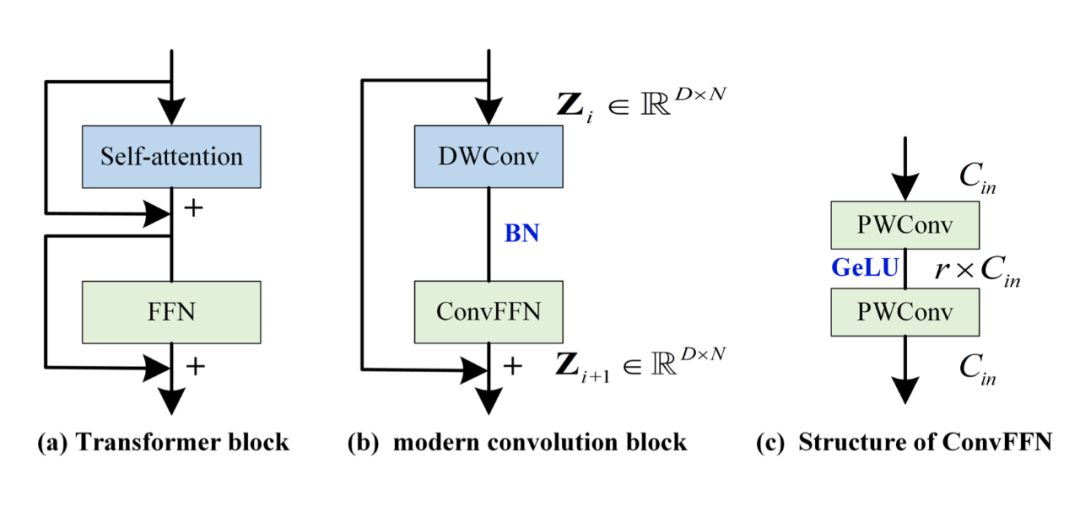
然而,作者發現采用上圖(b)的結構構建的模型效果也不是特別好,這是因為這個現代卷積結構中并沒有專門為時間序列設計的一些特殊的東西,一個重要的就是如何建模跨變量依賴性。注意,在這里要區分通道和變量之間的關系。變量是指多變量序列中每個變量,通道是指每個變量映射到的隱空間維度(而 PatchTST 中提到的通道獨立則是變量之間獨立,這個不要混淆)。ConvFFN 可以建模通道間關系,但無法建模變量間關系。
1.3 適用于時間序列的改動(變量間建模)
首先,在 embedding 的過程中,cv 一般是直接混合 RGB 變量。而在時間序列中,這種方式不適用,因為一個簡單的 embedding 顯然無法充分建模變量間關系。如果在 embedding 時就已經把變量混合了起來,那后續對變量間的建模則是混亂的。
因此,作者提出了變量無關 embedding,也是用了分 patch 的方法,對每個變量獨立分 patch 進行 embedding。具體在代碼實現上,作者是采用有 stride 的卷積,在這里我給出了代碼實現,先介紹下代碼相關的注釋:
# B:batch size
# M:多變量序列的變量數
# L:過去序列的長度
#T:預測序列的長度
#N:分Patch后Patch的個數
# D:每個變量的通道數
# P:kernel size of embedding layer
# S:stride of embedding layer
classEmbedding(nn.Module):
def__init__(self,P=8,S=4,D=2048):
super(Embedding,self).__init__()
self.P=P
self.S=S
self.conv=nn.Conv1d(
in_channels=1,
out_channels=D,
kernel_size=P,
stride=S
)
defforward(self,x):
#x:[B,M,L]
B=x.shape[0]
x=x.unsqueeze(2)#[B,M,L]->[B,M,1,L]
x=rearrange(x,'bmrl->(bm)rl')#[B,M,1,L]->[B*M,1,L]
x_pad=F.pad(
x,
pad=(0,self.P-self.S),
mode='replicate'
)#[B*M,1,L]->[B*M,1,L+P-S]
x_emb=self.conv(x_pad)#[B*M,1,L+P-S]->[B*M,D,N]
x_emb=rearrange(x_emb,'(bm)dn->bmdn',b=B)#[B*M,D,N]->[B,M,D,N]
returnx_emb#x_emb:[B,M,D,N]
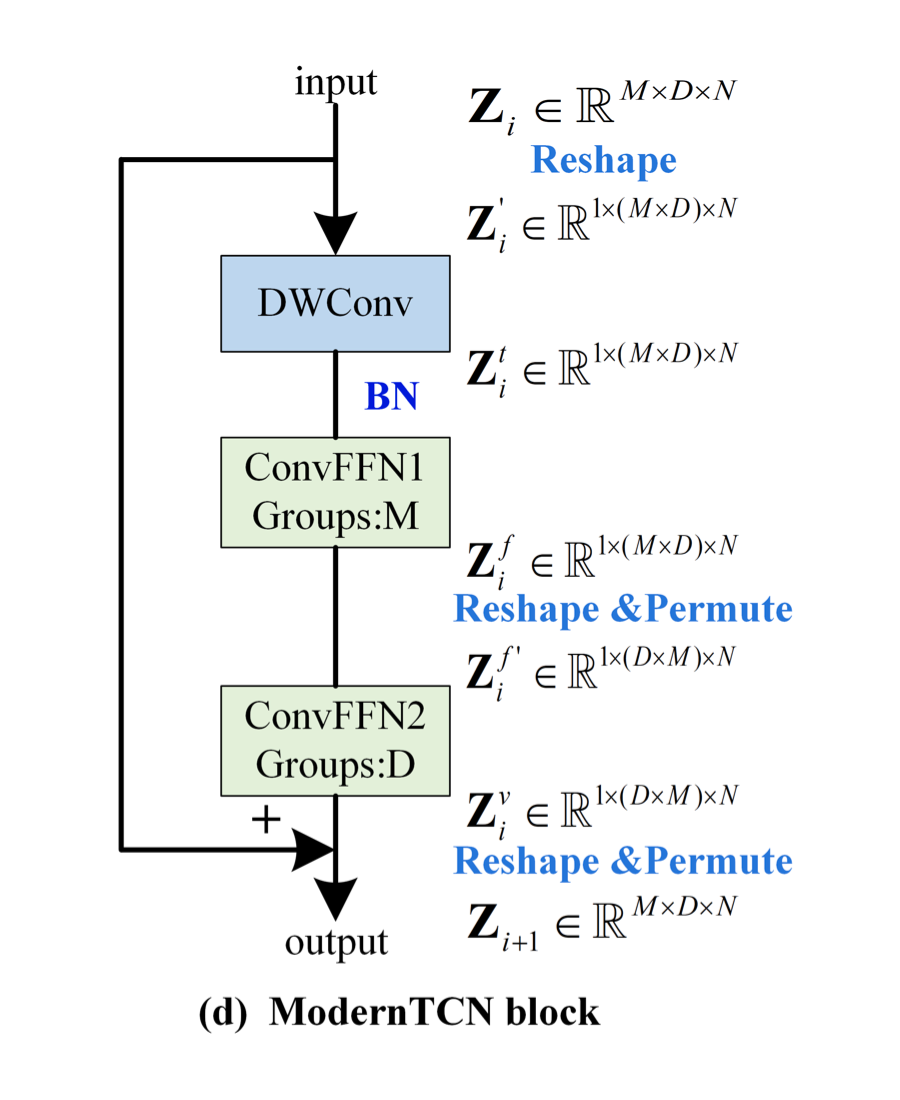
上圖中 DWconv 用來建模時間關系,第一個 ConvFFN 用來建模通道關系,第二個 ConvFFN 用來建模變量關系。下面介紹具體的實現,注意看上圖中 shape 在每一個模塊的前后變化。
首先,希望用 DWConv 來建模時間上的關系,但又不希望它參與到通道間和變量間的建模上。因此,作者將 M 和 D 這兩個表示變量和通道的維度 reshape 在一起,再進行深度可分離卷積。
其次,希望獨立建模通道和變量。因此,作者采用了兩個組卷積,其中一個組卷積的 Group 數為 M(表示每 D 個通道構成一個組,因此用來建模通道間關系),另一個組卷積的 Group 數為 D(表示每 M 個變量構成一個組,因此用來建模變量間關系)。注意,兩個組卷積之間存在著 reshape 和 permute 操作,這是為了正確的分組,最后會再 reshape 和 permute 回去。
最后,整體再用一個殘差連接,即可得到最終的 ModernTCN block。ModernTCN block 的代碼實現在最后,堆疊多個 block 即可得到 ModernTCN 模型。
綜上所述,作者將時間上、通道上、變量上的三種關系解耦建模,用三種組卷積來巧妙地進行實現(深度可分離卷積其實也是組數等于深度數的組卷積),既簡單又有效。

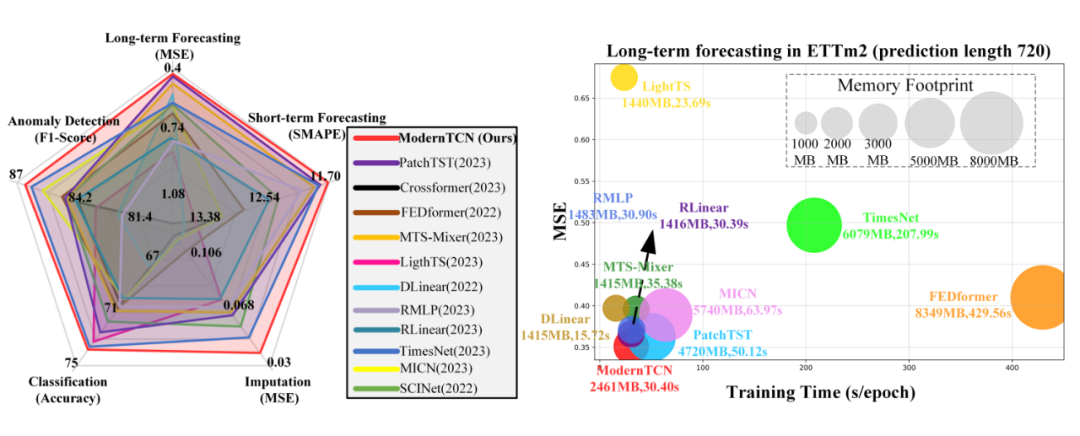
實驗
作者也是在各種時間序列任務上進行了實驗,如下圖,又快又好的五邊形戰士:

代碼實現
注意,我這里實現的模型是用于時間序列預測任務的,在 backbone 的基礎上加了個預測頭,具體的結構在論文附錄圖 5。
importtorch
importtorch.nnasnn
importtorch.nn.functionalasF
fromeinopsimportrearrange
# B:batch size
# M:多變量序列的變量數
# L:過去序列的長度
#T:預測序列的長度
#N:分Patch后Patch的個數
# D:每個變量的通道數
# P:kernel size of embedding layer
# S:stride of embedding layer
classEmbedding(nn.Module):
def__init__(self,P=8,S=4,D=2048):
super(Embedding,self).__init__()
self.P=P
self.S=S
self.conv=nn.Conv1d(
in_channels=1,
out_channels=D,
kernel_size=P,
stride=S
)
defforward(self,x):
#x:[B,M,L]
B=x.shape[0]
x=x.unsqueeze(2)#[B,M,L]->[B,M,1,L]
x=rearrange(x,'bmrl->(bm)rl')#[B,M,1,L]->[B*M,1,L]
x_pad=F.pad(
x,
pad=(0,self.P-self.S),
mode='replicate'
)#[B*M,1,L]->[B*M,1,L+P-S]
x_emb=self.conv(x_pad)#[B*M,1,L+P-S]->[B*M,D,N]
x_emb=rearrange(x_emb,'(bm)dn->bmdn',b=B)#[B*M,D,N]->[B,M,D,N]
returnx_emb#x_emb:[B,M,D,N]
classConvFFN(nn.Module):
def__init__(self,M,D,r,one=True):#oneisTrue:ConvFFN1,oneisFalse:ConvFFN2
super(ConvFFN,self).__init__()
groups_num=MifoneelseD
self.pw_con1=nn.Conv1d(
in_channels=M*D,
out_channels=r*M*D,
kernel_size=1,
groups=groups_num
)
self.pw_con2=nn.Conv1d(
in_channels=r*M*D,
out_channels=M*D,
kernel_size=1,
groups=groups_num
)
defforward(self,x):
#x:[B,M*D,N]
x=self.pw_con2(F.gelu(self.pw_con1(x)))
returnx#x:[B,M*D,N]
classModernTCNBlock(nn.Module):
def__init__(self,M,D,kernel_size,r):
super(ModernTCNBlock,self).__init__()
#深度分離卷積負責捕獲時域關系
self.dw_conv=nn.Conv1d(
in_channels=M*D,
out_channels=M*D,
kernel_size=kernel_size,
groups=M*D,
padding='same'
)
self.bn=nn.BatchNorm1d(M*D)
self.conv_ffn1=ConvFFN(M,D,r,one=True)
self.conv_ffn2=ConvFFN(M,D,r,one=False)
defforward(self,x_emb):
#x_emb:[B,M,D,N]
D=x_emb.shape[-2]
x=rearrange(x_emb,'bmdn->b(md)n')#[B,M,D,N]->[B,M*D,N]
x=self.dw_conv(x)#[B,M*D,N]->[B,M*D,N]
x=self.bn(x)#[B,M*D,N]->[B,M*D,N]
x=self.conv_ffn1(x)#[B,M*D,N]->[B,M*D,N]
x=rearrange(x,'b(md)n->bmdn',d=D)#[B,M*D,N]->[B,M,D,N]
x=x.permute(0,2,1,3)#[B,M,D,N]->[B,D,M,N]
x=rearrange(x,'bdmn->b(dm)n')#[B,D,M,N]->[B,D*M,N]
x=self.conv_ffn2(x)#[B,D*M,N]->[B,D*M,N]
x=rearrange(x,'b(dm)n->bdmn',d=D)#[B,D*M,N]->[B,D,M,N]
x=x.permute(0,2,1,3)#[B,D,M,N]->[B,M,D,N]
out=x+x_emb
returnout#out:[B,M,D,N]
classModernTCN(nn.Module):
def__init__(self,M,L,T,D=2048,P=8,S=4,kernel_size=51,r=1,num_layers=2):
super(ModernTCN,self).__init__()
#深度分離卷積負責捕獲時域關系
self.num_layers=num_layers
N=L//S
self.embed_layer=Embedding(P,S,D)
self.backbone=nn.ModuleList([ModernTCNBlock(M,D,kernel_size,r)for_inrange(num_layers)])
self.head=nn.Linear(D*N,T)
defforward(self,x):
#x:[B,M,L]
x_emb=self.embed_layer(x)#[B,M,L]->[B,M,D,N]
foriinrange(self.num_layers):
x_emb=self.backbone[i](x_emb)#[B,M,D,N]->[B,M,D,N]
#Flatten
z=rearrange(x_emb,'bmdn->bm(dn)')#[B,M,D,N]->[B,M,D*N]
pred=self.head(z)#[B,M,D*N]->[B,M,T]
returnpred#out:[B,M,T]
past_series=torch.rand(2,4,96)
model=ModernTCN(4,96,192)
pred_series=model(past_series)
print(pred_series.shape)
#torch.Size([2,4,192])

Comments
附錄很長,里面的消融實驗很充分,效果也很好,想法很合理,實現起來也很簡單,估計能中 oral。不過感覺在那幾個時間序列預測任務上的數據集都快刷爆了,性能快到瓶頸了,感覺之后很難再有大的效果提升了。
-
物聯網
+關注
關注
2914文章
45007瀏覽量
377691
原文標題:ICLR 2024高分投稿:用于一般時間序列分析的現代純卷積結構
文章出處:【微信號:tyutcsplab,微信公眾號:智能感知與物聯網技術研究所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
使用BP神經網絡進行時間序列預測
光譜傳感器的一般原理
如何使用RNN進行時間序列預測
【「時間序列與機器學習」閱讀體驗】時間序列的信息提取
卷積神經網絡的基本結構和工作原理
卷積神經網絡的一般步驟是什么
卷積神經網絡的基本結構及其功能
卷積神經網絡的基本原理、結構及訓練過程
名單公布!【書籍評測活動NO.35】如何用「時間序列與機器學習」解鎖未來?
數控加工工藝分析的一般步驟與方法
深度學習在時間序列預測的總結和未來方向分析





 ICLR 2024高分投稿:用于一般時間序列分析的現代純卷積結構
ICLR 2024高分投稿:用于一般時間序列分析的現代純卷積結構










評論