Part 01
前言
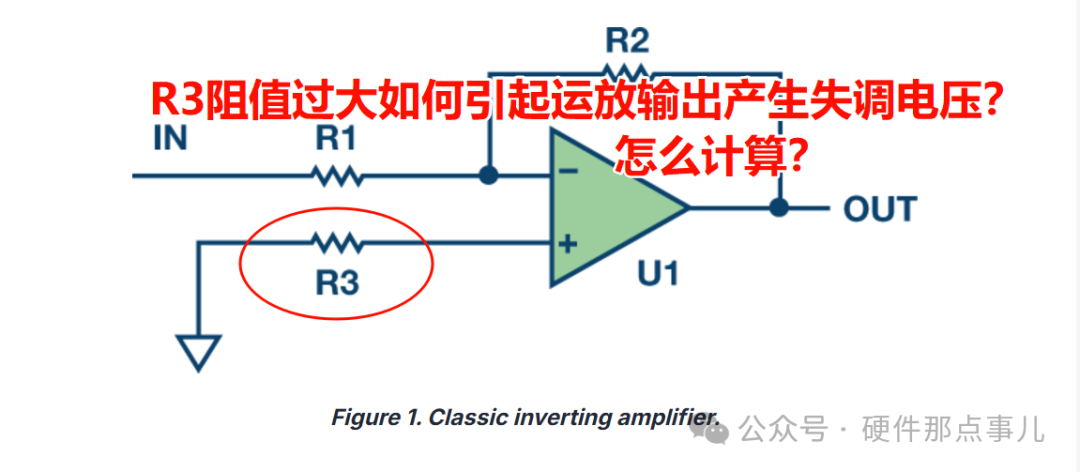
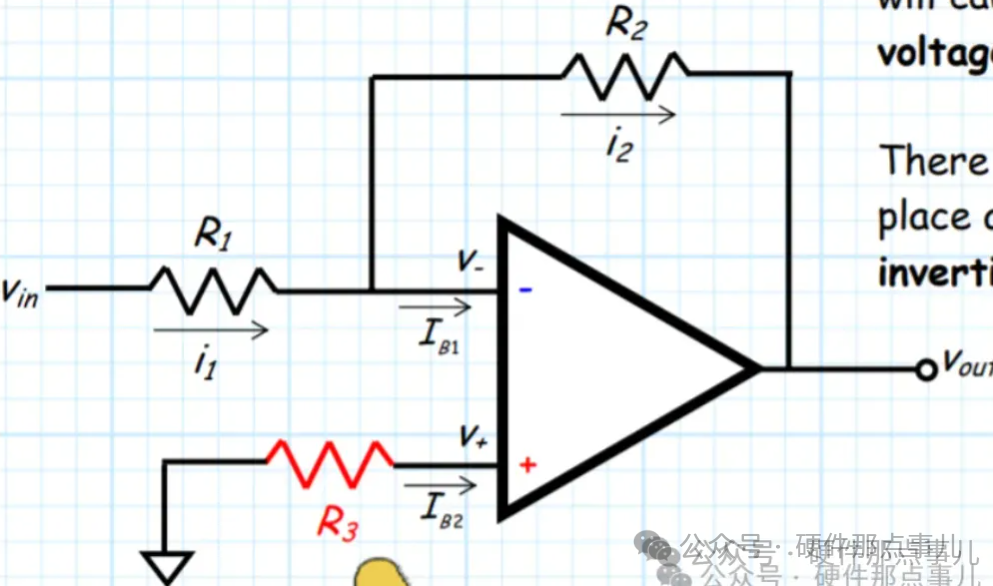
當(dāng)我們用運(yùn)放設(shè)計(jì)電流或者電壓采樣電路時(shí),如果我們要求的采樣精度比較高的話,那么一個(gè)繞不開(kāi)的話題就是噪聲,噪聲是很多硬件工程師容易忽視又不知如何下手的因素,但是噪聲影響是信號(hào)處理中的一個(gè)重要問(wèn)題,它會(huì)影響采樣電路的精度和穩(wěn)定性,運(yùn)放電路中的噪聲分為兩大類(lèi),一類(lèi)是運(yùn)放內(nèi)部噪聲的影響,另外一類(lèi)是運(yùn)放外部噪聲的影響,而電阻的熱噪聲是運(yùn)放外部噪聲影響因素中的一種。 在之前的文章中我們介紹過(guò)為了解決運(yùn)放偏置電流引起的輸入失調(diào)電壓,會(huì)在反相放大電路的同相輸入端串聯(lián)一個(gè)電阻,如果R3匹配電阻的阻值比較大的話,會(huì)引入額外的噪聲,進(jìn)而在運(yùn)放輸出端產(chǎn)生失調(diào)電壓,如何計(jì)算這個(gè)噪聲呢?
Part 02
如何理解噪聲?
噪聲是什么?噪聲在電路中本質(zhì)上還是一種信號(hào),只不過(guò)它不是你想要的信號(hào),它可能是電流信號(hào),也可能是電壓信號(hào)。電路中的噪聲是一種隨機(jī)信號(hào),為什么隨機(jī)呢?如果你對(duì)“電子”還有印象,這玩意就是隨機(jī)亂跑亂撞,雖然是隨機(jī)的,但是呢它又符合一定的概率分布特性和統(tǒng)計(jì)參數(shù),比如著名的分布噪聲分布曲線:正態(tài)分布,也叫高斯分布。
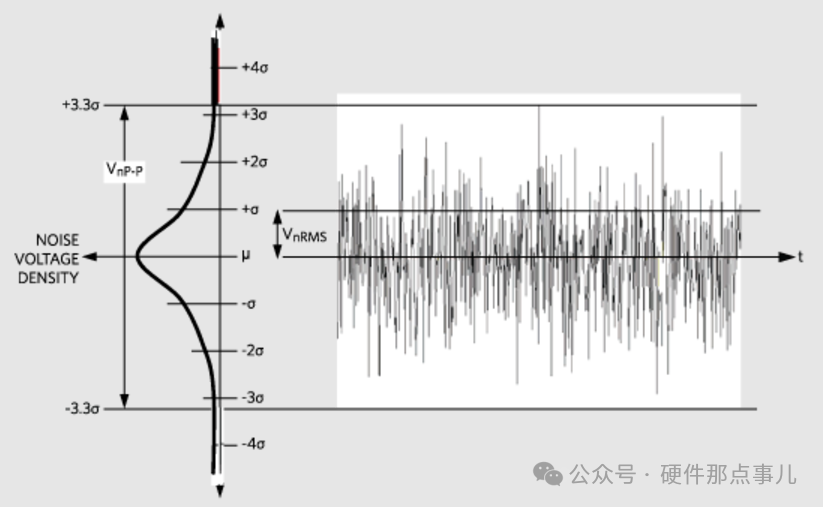
根據(jù)中心極限定理,當(dāng)大量獨(dú)立隨機(jī)變量疊加時(shí),其總和趨于服從正態(tài)分布,無(wú)論原始變量的分布是什么。因此,高斯分布是描述噪聲的自然選擇,尤其是由大量微觀事件疊加而成的噪聲,所以你看上面兩張圖,原本雜亂無(wú)章的噪聲分布經(jīng)過(guò)概率密度函數(shù)一分析,就變得很有章法,數(shù)學(xué)是不是很神奇,所以要想搞好電路,數(shù)學(xué)是基本功。 高斯分布的概率密度函數(shù)如下:
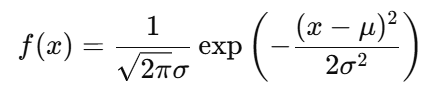
μ: 噪聲的平均值(μ反映噪聲信號(hào)的直流偏移量。理想情況下,噪聲的平均值為零,表示正負(fù)噪聲幅度對(duì)稱(chēng))
σ: 噪聲的標(biāo)準(zhǔn)差,表示噪聲的幅度的典型分布范圍。標(biāo)準(zhǔn)差是一組數(shù)據(jù)平均值分散程度的一種度量。一個(gè)較大的標(biāo)準(zhǔn)差,代表大部分?jǐn)?shù)值和其平均值之間差異較大。

如何理解高斯分布曲線?
在高斯分布中:
68.3%的噪聲幅度在±σ內(nèi)。
95.4%的噪聲幅度在±2σ內(nèi)。
99.7%的噪聲幅度在±3σ內(nèi)。
既然99.7%的噪聲幅度都在±3σ內(nèi),那么我們就能基于標(biāo)準(zhǔn)差σ計(jì)算得到噪聲的峰峰值,因?yàn)橹挥兄懒嗽肼暤姆宸逯挡拍芊奖阄覀冇?jì)算對(duì)測(cè)量信號(hào)的影響。噪聲的有效值約等于標(biāo)準(zhǔn)差σ(當(dāng)噪聲平均值為0時(shí)),這樣噪聲信號(hào)的峰峰值計(jì)算如下:
σ=Vrms
Vpp≈6*σ
這樣我們就能根據(jù)噪聲的正態(tài)分布曲線計(jì)算得到噪聲的峰峰值。
Part 03
如何計(jì)算電阻的熱噪聲
電阻熱噪聲是由電阻內(nèi)部自由電子的熱運(yùn)動(dòng)產(chǎn)生的無(wú)規(guī)則波動(dòng),噪聲幅值呈正態(tài)分布,其平均值為零。電阻熱噪聲電壓的計(jì)算為在電阻R上,帶寬B內(nèi)的熱噪聲均方根(RMS)電壓為:
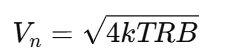
k=1.38×10^-23J/K,是玻爾茲曼常數(shù)
T:電阻的絕對(duì)溫度(開(kāi)爾文,K),T=273+攝氏溫度
R:電阻值(Ω)
B:噪聲的帶寬(Hz)
可以看出當(dāng)阻值一定,溫度一定時(shí),帶寬對(duì)噪聲的影響至關(guān)重要,帶寬越寬,噪聲越大。 比如環(huán)境溫度為25℃,電阻阻值為100K,帶寬為1Hz,可以計(jì)算得到電阻的熱噪聲為40nV。
Part 04
如何計(jì)算電阻的熱噪聲對(duì)運(yùn)放輸出的影響
如果下面的反相放大電路的放大倍數(shù)是100,電阻R3的阻值是100K,環(huán)境溫度是25℃,噪聲帶寬是100KHz的話,對(duì)應(yīng)的輸出噪聲電壓有效值為: Vos=40nV*√100KHz*100≈1.27mV 1.27mV的輸出失調(diào)電壓對(duì)于一些高精度信號(hào)測(cè)量來(lái)說(shuō)已經(jīng)是不小的影響了,所以如果你有高精度測(cè)量應(yīng)用,不可忽視電阻熱噪聲的影響!
-
串聯(lián)電阻
+關(guān)注
關(guān)注
1文章
203瀏覽量
15050 -
放大電路
+關(guān)注
關(guān)注
105文章
1811瀏覽量
107514 -
電路設(shè)計(jì)
+關(guān)注
關(guān)注
6689文章
2495瀏覽量
207565 -
運(yùn)放
+關(guān)注
關(guān)注
49文章
1184瀏覽量
53813 -
失調(diào)電壓
+關(guān)注
關(guān)注
0文章
165瀏覽量
14154
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
1200字搞懂運(yùn)放電路中輸入失調(diào)電壓的分析,計(jì)算,以及選型對(duì)策
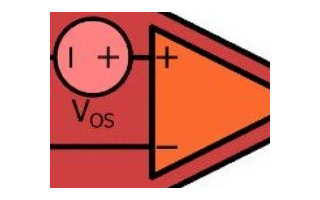
輸入失調(diào)電流造成的誤差是怎么計(jì)算得到的?
THS4303的輸出失調(diào)電壓很大,為什么?
VCA821輸出失調(diào)電壓遇到的疑問(wèn)求解
運(yùn)放輸入失調(diào)電壓的結(jié)構(gòu)和原理
如何降低TLV2711IDBVR的輸入失調(diào)電壓?
LM2904DR失調(diào)電壓影響輸出結(jié)果怎么解決?
運(yùn)放失調(diào)電壓補(bǔ)償方法有哪些
求助,幫忙看下以下測(cè)量運(yùn)放的輸入失調(diào)電壓Vos正確否?
INA819儀表放大器失調(diào)電壓怎么調(diào)零?
簡(jiǎn)述運(yùn)算放大器的失調(diào)電壓
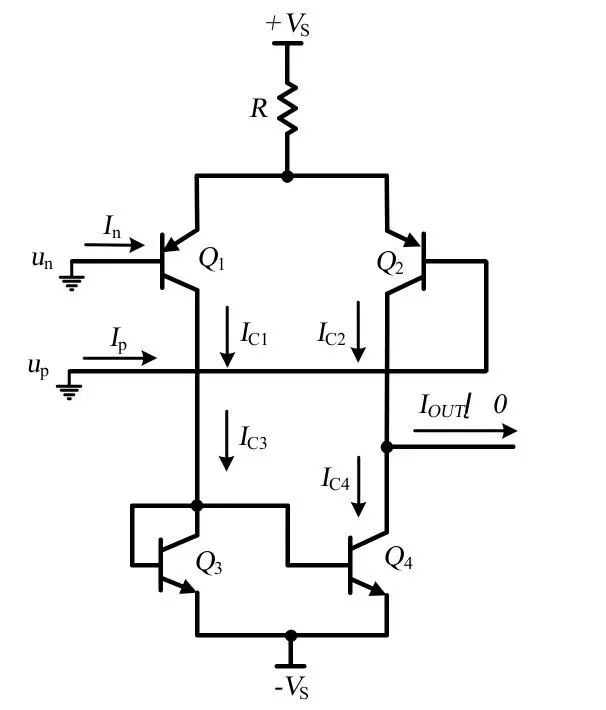
請(qǐng)問(wèn)運(yùn)放的輸入失調(diào)電壓會(huì)受輸入電壓影響嗎?
AMC1302失調(diào)電壓過(guò)大是怎么回事?
失調(diào)電壓/補(bǔ)償電壓你真的懂了嗎?






 反相放大電路運(yùn)放V+引腳串聯(lián)電阻過(guò)大也會(huì)產(chǎn)生輸出失調(diào)電壓?1400字理清原理與計(jì)算
反相放大電路運(yùn)放V+引腳串聯(lián)電阻過(guò)大也會(huì)產(chǎn)生輸出失調(diào)電壓?1400字理清原理與計(jì)算











評(píng)論