分支限界法與回溯法
(1)求解目標(biāo):回溯法的求解目標(biāo)是找出解空間樹中滿足約束條件的所有解,而分支限界法的求解目標(biāo)則是找出滿足約束條件的一個(gè)解,或是在滿足約束條件的解中找出在某種意義下的最優(yōu)解。 (2)搜索方式的不同:回溯法以深度優(yōu)先的方式搜索解空間樹,而分支限界法則以廣度優(yōu)先或以最小耗費(fèi)優(yōu)先的方式搜索解空間樹。
分支限界法的基本思想
分支限界法常以廣度優(yōu)先或以最小耗費(fèi)(最大效益)優(yōu)先的方式搜索問題的解空間樹。在分支限界法中,每一個(gè)活結(jié)點(diǎn)只有一次機(jī)會(huì)成為擴(kuò)展結(jié)點(diǎn)。活結(jié)點(diǎn)一旦成為擴(kuò)展結(jié)點(diǎn),就一次性產(chǎn)生其所有兒子結(jié)點(diǎn)。在這些兒子結(jié)點(diǎn)中,導(dǎo)致不可行解或?qū)е路亲顑?yōu)解的兒子結(jié)點(diǎn)被舍棄,其余兒子結(jié)點(diǎn)被加入活結(jié)點(diǎn)表中。 此后,從活結(jié)點(diǎn)表中取下一結(jié)點(diǎn)成為當(dāng)前擴(kuò)展結(jié)點(diǎn),并重復(fù)上述結(jié)點(diǎn)擴(kuò)展過程。這個(gè)過程一直持續(xù)到找到所需的解或活結(jié)點(diǎn)表為空時(shí)為止。
常見的兩種分支限界法
(1)隊(duì)列式(FIFO)分支限界法 按照隊(duì)列先進(jìn)先出(FIFO)原則選取下一個(gè)結(jié)點(diǎn)為擴(kuò)展結(jié)點(diǎn)。 (2)優(yōu)先隊(duì)列式分支限界法 按照優(yōu)先隊(duì)列中規(guī)定的優(yōu)先級(jí)選取優(yōu)先級(jí)最高的結(jié)點(diǎn)成為當(dāng)前擴(kuò)展結(jié)點(diǎn)。
一、單源最短路徑問題
1、問題描述
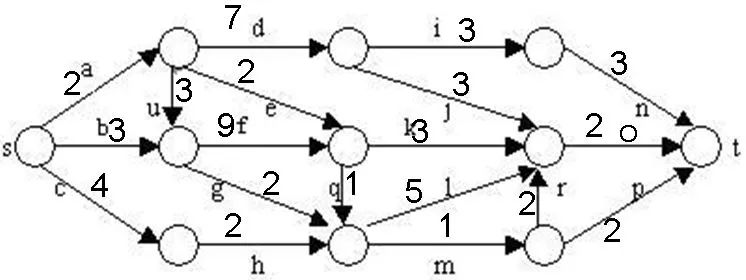
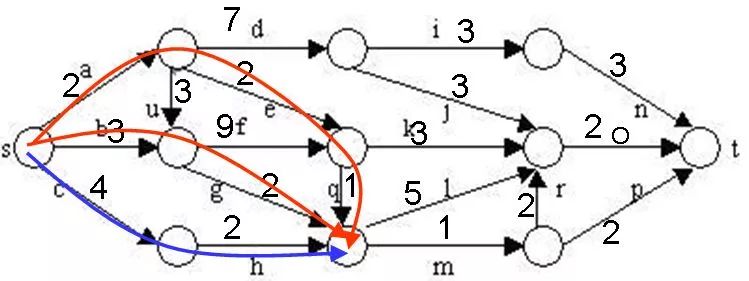
在下圖所給的有向圖G中,每一邊都有一個(gè)非負(fù)邊權(quán)。要求圖G的從源頂點(diǎn)s到目標(biāo)頂點(diǎn)t之間的最短路徑。
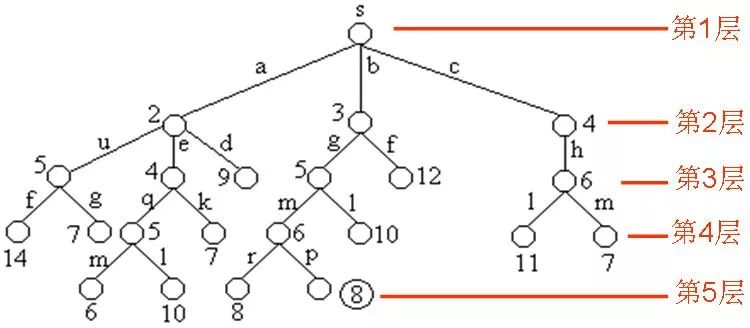
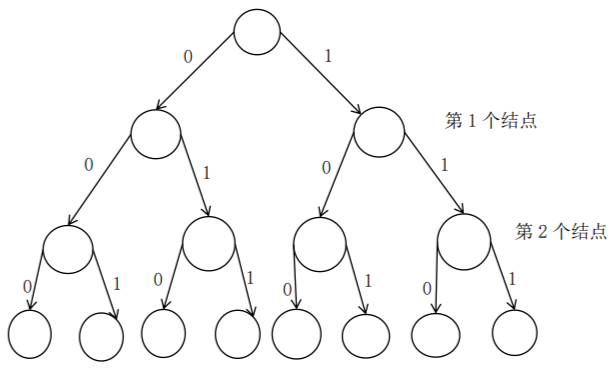
下圖是用優(yōu)先隊(duì)列式分支限界法解有向圖G的單源最短路徑問題產(chǎn)生的解空間樹。其中,每一個(gè)結(jié)點(diǎn)旁邊的數(shù)字表示該結(jié)點(diǎn)所對(duì)應(yīng)的當(dāng)前路長。
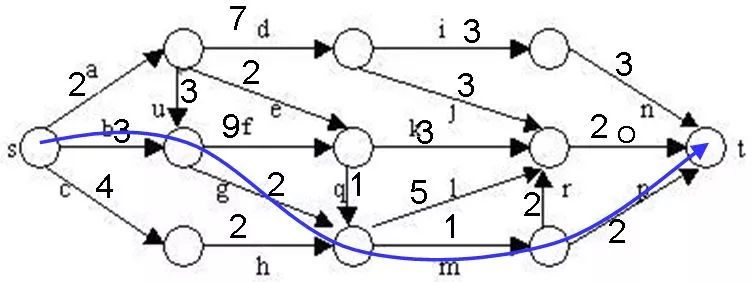
找到一條路徑:
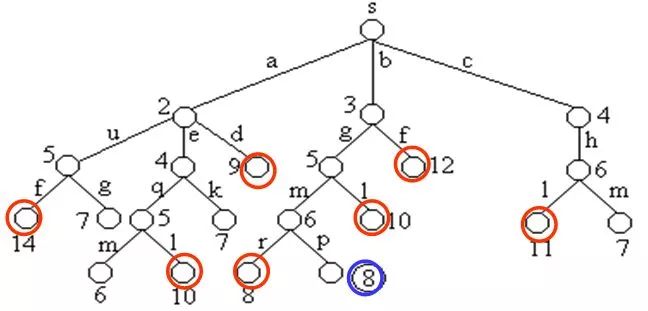
目前的最短路徑是8,一旦發(fā)現(xiàn)某個(gè)結(jié)點(diǎn)的下界不小于這個(gè)最短路進(jìn),則剪枝:
同一個(gè)結(jié)點(diǎn)選擇最短的到達(dá)路徑:
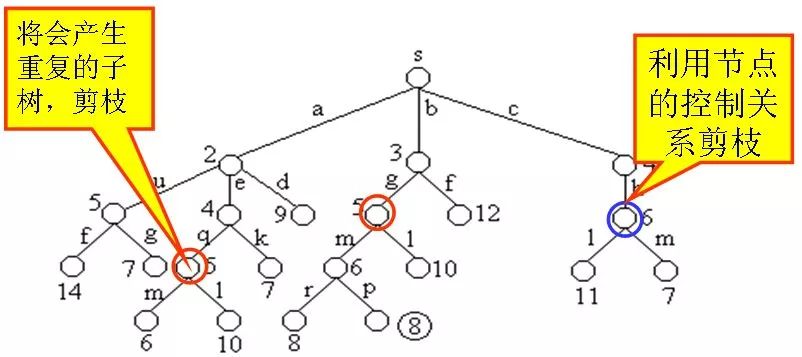
2.剪枝策略
在算法擴(kuò)展結(jié)點(diǎn)的過程中,一旦發(fā)現(xiàn)一個(gè)結(jié)點(diǎn)的下界不小于當(dāng)前找到的最短路長,則算法剪去以該結(jié)點(diǎn)為根的子樹。
在算法中,利用結(jié)點(diǎn)間的控制關(guān)系進(jìn)行剪枝。從源頂點(diǎn)s出發(fā),2條不同路徑到達(dá)圖G的同一頂點(diǎn)。由于兩條路徑的路長不同,因此可以將路長長的路徑所對(duì)應(yīng)的樹中的結(jié)點(diǎn)為根的子樹剪去。
3.算法思想
解單源最短路徑問題的優(yōu)先隊(duì)列式分支限界法用一極小堆來存儲(chǔ)活結(jié)點(diǎn)表。其優(yōu)先級(jí)是結(jié)點(diǎn)所對(duì)應(yīng)的當(dāng)前路長。
算法從圖G的源頂點(diǎn)s和空優(yōu)先隊(duì)列開始。結(jié)點(diǎn)s被擴(kuò)展后,它的兒子結(jié)點(diǎn)被依次插入堆中。此后,算法從堆中取出具有最小當(dāng)前路長的結(jié)點(diǎn)作為當(dāng)前擴(kuò)展結(jié)點(diǎn),并依次檢查與當(dāng)前擴(kuò)展結(jié)點(diǎn)相鄰的所有頂點(diǎn)。如果從當(dāng)前擴(kuò)展結(jié)點(diǎn)i到頂點(diǎn)j有邊可達(dá),且從源出發(fā),途經(jīng)頂點(diǎn)i再到頂點(diǎn)j的所相應(yīng)的路徑的長度小于當(dāng)前最優(yōu)路徑長度,則將該頂點(diǎn)作為活結(jié)點(diǎn)插入到活結(jié)點(diǎn)優(yōu)先隊(duì)列中。這個(gè)結(jié)點(diǎn)的擴(kuò)展過程一直繼續(xù)到活結(jié)點(diǎn)優(yōu)先隊(duì)列為空時(shí)為止。
實(shí)現(xiàn)
* 作者:chinazhangjie
* 郵箱:chinajiezhang@gmail.com
* 開發(fā)語言:C++
* 開發(fā)環(huán)境:Mircosoft Virsual Studio 2008
* 時(shí)間: 2010.11.01
*/
#include
#include
#include
#include
using namespacestd;
structnode_info
{
public:
node_info(inti,intw)
: index(i),weight(w){}
node_info()
: index(0),weight(0){}
node_info(constnode_info & ni)
: index(ni.index),weight(ni.weight){}
friend
booloperator < (constnode_info& lth,constnode_info& rth){
returnlth.weight > rth.weight;// 為了實(shí)現(xiàn)從小到大的順序
}
public:
intindex;// 結(jié)點(diǎn)位置
intweight;// 權(quán)值
};
structpath_info
{
public:
path_info()
: front_index(0),weight(numeric_limits
public:
intfront_index;
intweight;
};
// single source shortest paths
classss_shortest_paths
{
public:
ss_shortest_paths(constvector
:no_edge(-1),end_node(end_location),node_count(g.size()),graph(g)
{}
// 打印最短路徑
voidprint_spaths()const{
cout << "min weight : " << shortest_path << endl;
cout << "path: ";
copy(s_path_index.rbegin(),s_path_index.rend(),
ostream_iterator
cout << endl;
}
// 求最短路徑
voidshortest_paths(){
vector
priority_queue
min_heap.push(node_info(0,0));// 將起始結(jié)點(diǎn)入隊(duì)
while(true){
node_info top = min_heap.top();// 取出最大值
min_heap.pop();
// 已到達(dá)目的結(jié)點(diǎn)
if(top.index == end_node){
break;
}
// 未到達(dá)則遍歷
for(inti = 0;i < node_count; ++ i){
// 頂點(diǎn)top.index和i間有邊,且此路徑長小于原先從原點(diǎn)到i的路徑長
if(graph[top.index][i] != no_edge &&
(top.weight + graph[top.index][i]) < path[i].weight){
min_heap.push(node_info(i,top.weight + graph[top.index][i]));
path[i].front_index = top.index;
path[i].weight = top.weight + graph[top.index][i];
}
}
if(min_heap.empty()){
break;
}
}
shortest_path = path[end_node].weight;
intindex = end_node;
s_path_index.push_back(index);
while(true){
index = path[index].front_index;
s_path_index.push_back(index);
if(index == 0){
break;
}
}
}
private:
vector
intnode_count;// 結(jié)點(diǎn)個(gè)數(shù)
constintno_edge;// 無通路
constintend_node;// 目的結(jié)點(diǎn)
vector
intshortest_path;// 最短路徑
};
intmain()
{
constintsize = 11;
vector
for(inti = 0;i < size; ++ i){
graph[i].resize(size);
}
for(inti = 0;i < size; ++ i){
for(intj = 0;j < size; ++ j){
graph[i][j] = -1;
}
}
graph[0][1] = 2;
graph[0][2] = 3;
graph[0][3] = 4;
graph[1][2] = 3;
graph[1][5] = 2;
graph[1][4] = 7;
graph[2][5] = 9;
graph[2][6] = 2;
graph[3][6] = 2;
graph[4][7] = 3;
graph[4][8] = 3;
graph[5][6] = 1;
graph[5][8] = 3;
graph[6][9] = 1;
graph[6][8] = 5;
graph[7][10] = 3;
graph[8][10] = 2;
graph[9][8] = 2;
graph[9][10] = 2;
ss_shortest_paths ssp(graph,10);
ssp.shortest_paths();
ssp.print_spaths();
return0;
}
測(cè)試數(shù)據(jù)(圖)
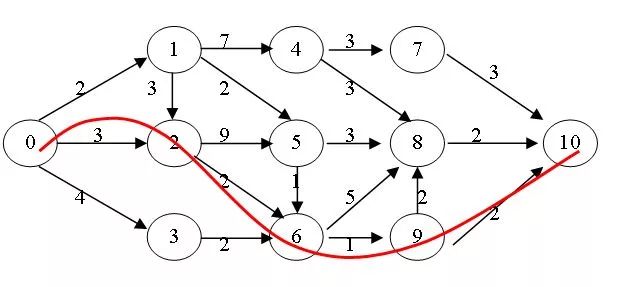
測(cè)試結(jié)果
-
算法
+關(guān)注
關(guān)注
23文章
4709瀏覽量
95334 -
fifo
+關(guān)注
關(guān)注
3文章
400瀏覽量
44801 -
回溯法
+關(guān)注
關(guān)注
0文章
2瀏覽量
6183
原文標(biāo)題:分支限界法
文章出處:【微信號(hào):TheAlgorithm,微信公眾號(hào):算法與數(shù)據(jù)結(jié)構(gòu)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
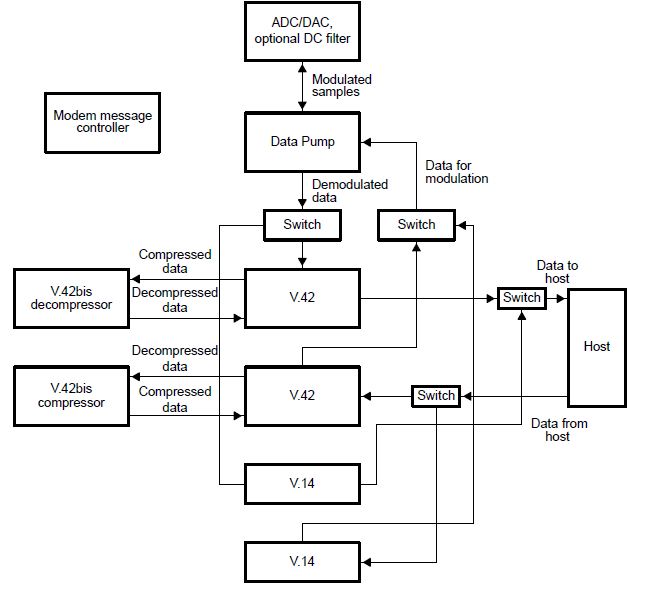
調(diào)制解調(diào)器和積分器算法程序的詳細(xì)資料概述
五大常用算法之回溯法

TI的基于DSP兼容的第三方算法協(xié)議的詳細(xì)資料概述
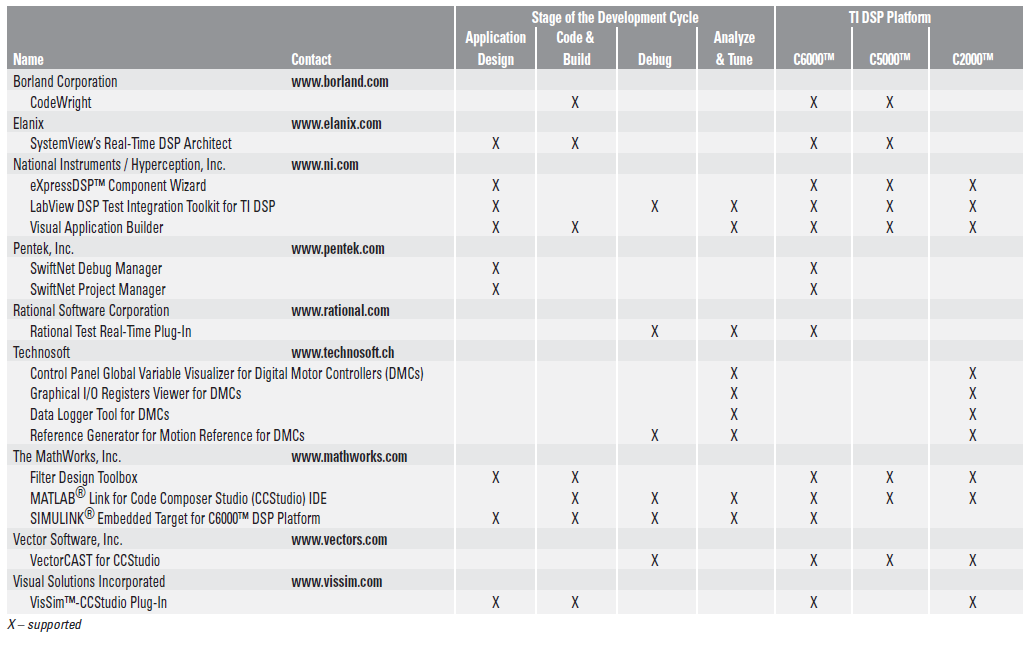
PID程序算法的詳細(xì)資料概述免費(fèi)下載
十一個(gè)經(jīng)典的濾波算法的介紹和示例程序詳細(xì)資料免費(fèi)下載
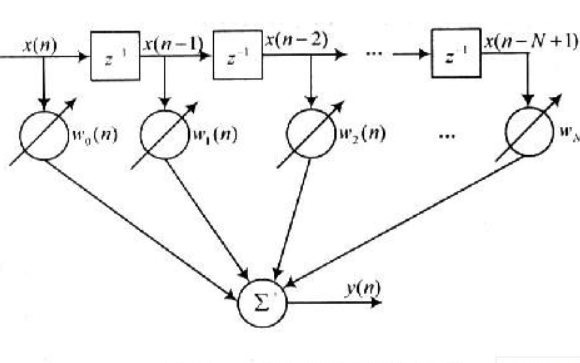
線性系統(tǒng)的頻域分析頻率特性法的詳細(xì)資料免費(fèi)下載
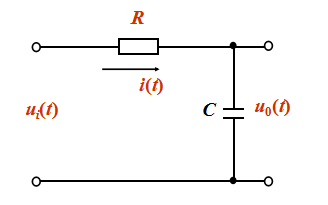
5500極譜法DO探頭校準(zhǔn)及維護(hù)的資料說明
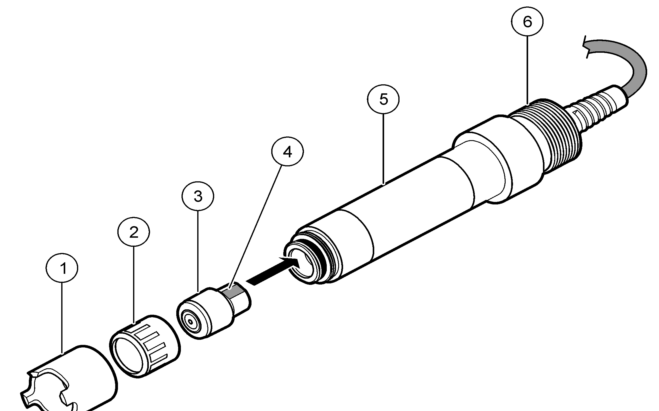
單片機(jī)有哪些常用濾波算法詳細(xì)資料說明
分形插值算法的詳細(xì)資料說明

龍格-庫塔法的MATLAB代碼及含義的詳細(xì)資料說明
python的內(nèi)置函數(shù)詳細(xì)資料概述
如何使用回溯法實(shí)現(xiàn)網(wǎng)絡(luò)設(shè)計(jì)問題算法的設(shè)計(jì)





 分支限界法與回溯法算法的詳細(xì)資料概述
分支限界法與回溯法算法的詳細(xì)資料概述












評(píng)論