摘要：

為了確保第五代移動通信（5G）技術的可靠性、穩定性、高傳輸速率的優勢，基于具有線性編碼復雜度的迭代編碼算法，提出了混合校驗矩陣構造算法。該算法首先對傳統迭代編碼算法進行改進，使其適用于多元低密度奇偶校驗（NB-LDPC）碼；然后采用后向迭代法改變編碼方案和校驗矩陣構造方式使漸進邊增長（PEG）算法具有下三角結構，并將其作為基矩陣；最后采用改進后具有下三角結構的QC-LDPC算法生成循環移位矩陣和有限域系數矩陣，同時消除短環影響，從中選取最優的校驗矩陣。仿真結果表明，混合構造算法所構造的多元LDPC碼不僅具有線性的編碼和存儲復雜度，且有較強的糾錯能力。

?

0 引言

隨著移動互聯網和物聯網的不斷發展，第五代移動通信(Fifth-Generation Mobile Communication Technology，5G)面臨移動通信爆發式增長[1-2]。5G技術不僅需要大幅度提升頻譜利用效率，而且需要具備支持海量設備連接的能力[3-6]。由于低密度奇偶校驗(Low Density Parity Check，LDPC)碼具有高可靠性、快速收斂性及較強抗突發錯誤能力[7-8]，可以提高系統有效性[9-10]，使得3GPP RAN1會議在2016年確定在5G移動通信中使用LDPC碼作為移動帶寬eMBB業務數據的長碼塊編碼方案。

本文對2004年由王鵬提出的LDPC碼迭代編碼算法[11]進行改進，轉變為適用于多元LDPC碼的編碼算法，稱為多元迭代編碼算法；2005年，Hu Xiaoyu提出了漸進邊增長（Progressive Edge Growth，PEG）構造算法[12]，該算法譯碼性能好，但編碼復雜度較高。本文針對PEG算法具有高編碼復雜度這一缺點，提出改進的PEG算法，即irPEG算法；結構化構造算法，即QC-LDPC構造算法[13]，該算法復雜，譯碼性能差于隨機構造算法，但復雜度大幅度下降，硬件實現性強。本文提出一種改進的QC-LDPC算法，使校驗矩陣具有下三角結構，降低復雜度，加快收斂速度，構造出無短環的校驗矩陣。然后，從編碼復雜度和糾錯性能兩方面考慮，基于多元迭代編碼算法，提出混合構造算法，即HC構造算法，將隨機構造和結構化構造算法結合，irPEG算法構造基矩陣，改進的QC-LDPC算法生成循環移位矩陣和有限域系數矩陣，消除短環影響，設置校驗矩陣個數，從中選取最優校驗矩陣。該算法既具有隨機構造的隨機性，又保持結構化構造的低復雜度，降低結構化構造對誤碼性能帶來的損失，是比較折中的算法。

1 多元迭代編碼算法

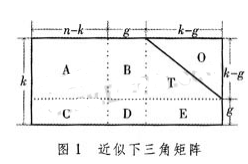
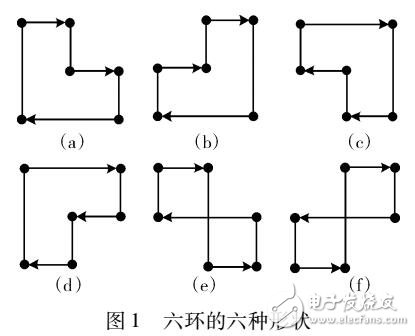
在圖1中對角線上的元素全部為GF(q)域上的非“0”元素，并且剩余的非“0”元素全部對應于對角線左邊。若構造出的多元LDPC校驗矩陣具有圖1的結構，則在編碼過程中可直接采用迭代編碼算法編碼。

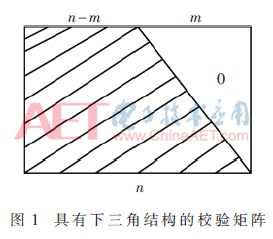
其中，l∈[0，n-k-1]，hi，j表示校驗矩陣H中第i行j列上的元素，且k=n-m。由式(1)知，多元迭代編碼算法過程為利用校驗矩陣H中各行約束關系，采用后項迭代算法，逐次計算每個校驗位符號值。

對迭代編碼算法改進，將二元迭代編碼時采用的與(AND)和異或(XOR)運算，改進為GF(q)域上乘法和加法運算。同時多元迭代編碼算法的運算過程中引入了GF(q)域上除法運算。對運算量簡化，將對角線上元素設置為1，式(1)改為式(2)。

2 混合構造算法

2.1 irPEG構造算法

針對PEG算法具有較高編碼復雜度的缺點，提出一種具有下三角結構非規則的PEG算法，即irPEG算法。該算法從編碼方案、構造校驗矩陣方面改進，以降低編碼復雜度，提升糾錯性能。具體步驟如下：

(1)確定基矩陣中各參數

行列數、變量節點度分布序列，并且初始化基矩陣的信息，包括與變量節點相互連接的校驗節點的集合以及它的補集。

(2)構造基矩陣對角線右側下三角部分

首先采用后項迭代算法從最后一列變量節點構造，根據變量節點度分布[14]向前連接校驗節點。每列中第一個非“0”元素位置必須與對角線上校驗節點連接，其余非“0”元素需添加在對角線左側。尋找所有與該變量節點連接的校驗節點集合，從中篩選度數最小的校驗節點集合。若該集合含有多元素，則從中刪除構成短環的校驗節點，隨機連接剩余某校驗節點，若只有一個元素，則直接連接該校驗節點。

(3)構造基矩陣的前n-m列

從第n-m個變量節點依次向前構造。根據初始化變量節點度分布序列選擇度數最小的校驗節點，保證每行行重相比于平均行重相差不大。刪除構成短環的校驗節點后，從剩余校驗節點中隨機連接。

由于構造出的矩陣具有下三角結構，構造時在滿足式(4)度分布的基礎上，將矩陣最后一列列重設置為1，校驗部分對角線上元素均為1，下三角部分均為0元素。由此可見，可以利用式(2)直接采用后多元迭代編碼算法進行編碼。

2.2 混合構造算法

雖然irPEG算法結合多元迭代編碼算法可大大降低編碼復雜度，但更適用于中短碼硬件實現，對于長碼來說，硬件實現復雜度依然較高。此時犧牲多元LDPC碼一定糾錯性能，在改進的QC-LDPC算法的基礎上使其具有下三角結構，同時采用irPEG算法構造基矩陣WJ×L，提高多元LDPC碼隨機性，降低結構化構造對糾錯性能帶來的損失。將改進的QC-LDPC構造算法與irPEG算法結合，稱為混合構造算法，即HC構造算法。HC構造算法步驟如下：

(1)irPEG算法構造基矩陣WJ×L。

給定多元LDPC碼度分布，根據irPEG算法構造出具有下三角結構二元基矩陣，大小為J×L。

(2)確定有限域元素系數矩陣GcJ×L，根據基矩陣非“0”元素位置，在(0，q-1)間隨機選擇gcj，l值。

(3)基矩陣WJ×L確定循環移位系數矩陣SJ×L。

將循環移位系數矩陣SJ×L對角線上系數設為0，隨機選擇移位系數sj，l，通過WJ×L結合避免長度為2i的充分必要條件，如式(5)所示，確定移位系數矩陣SJ×L中移位系數sj，l。

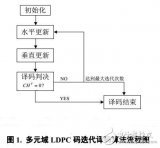
其中，0表示p×p維的零矩陣，P表示p×p維的單位陣，碼長為n=p×L，碼率為r=(1-J/L)。HC構造算法的流程圖如圖2所示。

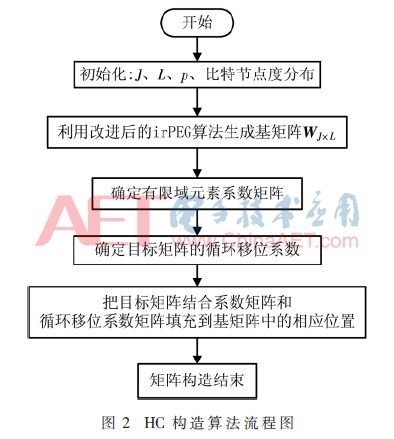
3 編碼復雜度分析

PEG算法、irPEG算法、HC算法的編碼復雜度如表1所示。其中，w是生成矩陣的平均列重，n是碼長，k是信息位長。

在存儲復雜度方面，HC算法構造的LDPC碼存儲矩陣時存儲一個p×p維目標方陣P、一個J×L維多元系數矩陣GcJ×L及一個J×L循環移位系數矩陣SJ×L。irPEG算法構造同樣大小校驗矩陣，存儲一個p×J×p×L大小的校驗矩陣。可見，HC算法與irPEG算法相比具有更簡單的矩陣存儲結構。

在編碼復雜度方面，PEG算法采用高斯消去編碼算法，irPEG算法和HC算法采用多元迭代編碼算法。高斯消去編碼復雜度包含預處理，運算復雜度為o(n3)，編碼復雜度為o(n2)，整個編碼過程需wn次乘法，(w-1)n次加法。多元迭代編碼算法整個編碼過程用到(w-1)(n-k)次加法，w(n-k)次乘法。

irPEG算法和HC算法能直接構造出下三角校驗矩陣，避免了校驗矩陣預處理的同時保證了校驗矩陣的稀疏性。因此，w相對于n可以看成非常小的常數，實現多元LDPC碼的線性復雜度編碼，與傳統的構造算法相比，大幅度地降低了編碼的復雜度。

4 仿真結果及分析

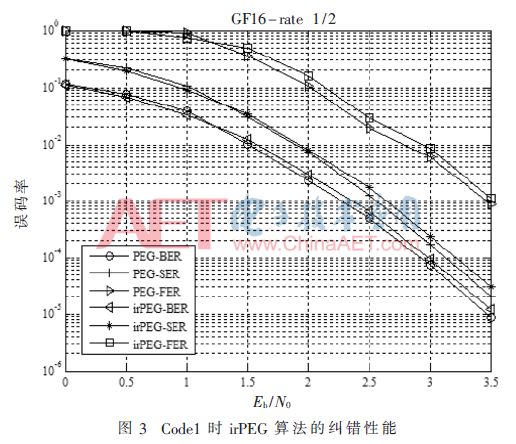
仿真參數設置：度分布服從式(4)的多元LDPC碼，矩陣通過PEG算法和irPEG算法生成，在十六進制1/2碼率（Code1）和3/4碼率（Code2）下進行仿真，Code1時，信息位長為512 bit；Code2時，信息位長為176 bit。譯碼采用Mixed Log-FFT-BP譯碼算法[15]，迭代次數25，BPSK調制，AWGN信道。

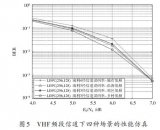
圖3和圖4分別為Code1和Code2時不同碼率下的糾錯性能。由圖3和圖4可知，irPEG算法與PEG算法誤碼率相比，性能相差不大，表明irPEG算法構造具有下三角結構的多元LDPC碼在大幅度降低硬件實現復雜度的同時，具有較強的糾錯能力。

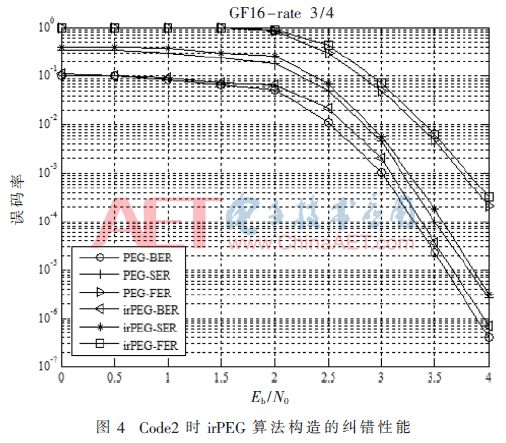
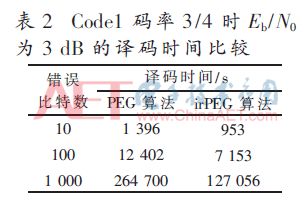
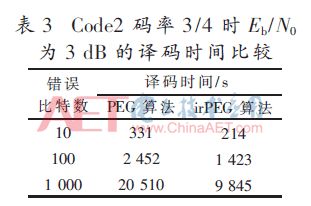
對Code1和Code2譯碼時間進行測量，保持仿真環境一致性，如表2和表3所示。由表2可知，irPEG算法時間明顯比PEG算法少，當誤比特數較少時，時間節省量少于50%，隨著誤比特數增加，時間節省量穩定在50%，因此，irPEG算法耗費時間僅為PEG算法50%。Code2在信噪比為4 dB時的仿真測試結果如表3所示，同樣表明譯碼所需時間減少一半。

參數設置如下：碼率1/2、2/3、3/4、4/5、6/7，矩陣通過PEG和HC生成，十六進制(Code3)下仿真，1/2碼率時，基矩陣16列，目標矩陣P為24×24單位陣；2/3碼率時，基矩陣18列，P為16×16單位陣；3/4碼率時，基矩陣16列，P為16×16單位陣；4/5碼率時，基矩陣20列，P為12×12單位陣；6/7碼率時，基矩陣14列，P為16×16單位陣，固定信息位長768 bit。圖5為Code3情況時，PEG算法與HC算法在不同碼率下的誤比特率性能。

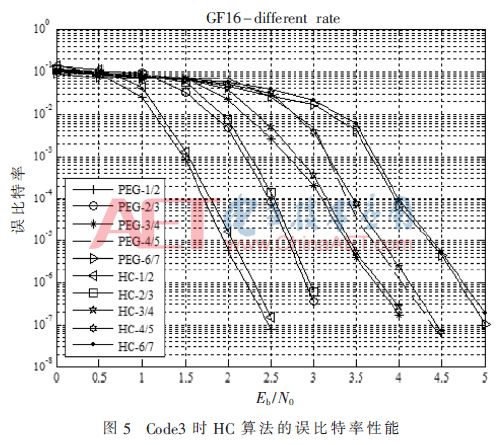
由圖5可知，HC算法與PEG算法構造的多元LDPC碼在低信噪比時沒有明顯差別；在高信噪比下HC算法性能略差于PEG算法構造的多元LDPC碼，因此兩種算法具有一致的編碼增益。

5 結論

本文提出基于多元LDPC碼迭代編碼算法的混合校驗矩陣構造算法，首先對迭代編碼算法改進，使其適用于多元LDPC碼；然后采用后項迭代法使PEG算法具有下三角結構，并將其作為混合構造算法基矩陣；最后采用改進后具有下三角的QC-LDPC碼算法生成循環移位矩陣和有限域系數矩陣，設置校驗矩陣的個數，從中選取最優的校驗矩陣，該校驗矩陣消除了短環影響，形成混合構造算法。仿真結果表明，本文提出的算法可以更好地適用于5G移動通信系統且滿足譯碼算法的需求，對于高速通信設備來說是一種很好的候選校驗矩陣構造算法。