訓練模型
一、討論兩種訓練方法二、線性回歸三、如何訓練四、正規方程五、示例六、模型圖像七、梯度下降八、梯度下降的陷阱
一、討論兩種訓練方法
1、直接使用封閉方程進行求根運算,得到模型在當前訓練集上的最優參數(即在訓練集上使損失函數達到最小值的模型參數)2、使用迭代優化方法:梯度下降(GD),在訓練集上,它可以逐漸調整模型參數以獲得最小的損失函數,最終,參數會收斂到和第一種方法相同的的值。同時,我們也會介紹一些梯度下降的變體形式:批量梯度下降(Batch GD)、小批量梯度下降(Mini-batch GD)、隨機梯度下降(Stochastic GD)。對于多項式回歸,它可以擬合非線性數據集,由于它比線性模型擁有更多的參數,于是它更容易出現模型的過擬合。因此,我們將介紹如何通過學習曲線去判斷模型是否出現了過擬合,并介紹幾種正則化方法以減少模型出現過擬合的風險。
二、線性回歸
線性回歸預測模型
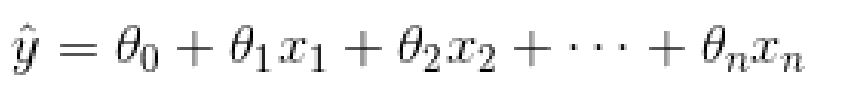

三、如何訓練
訓練一個模型指的是設置模型的參數使得這個模型在訓練集的表現較好。為此,我們首先需要找到一個衡量模型好壞的評定方法。在回歸模型上,最常見的評定標準是均方根誤差。因此,為了訓練一個線性回歸模型,需要找到一個θ值,它使得均方根誤差(標準誤差)達到最小值。實踐過程中,最小化均方誤差比最小化均方根誤差更加的簡單,這兩個過程會得到相同的θ因為函數在最小值時候的自變量,同樣能使函數的方根運算得到最小值。線性回歸模型的 MSE 損失函數:
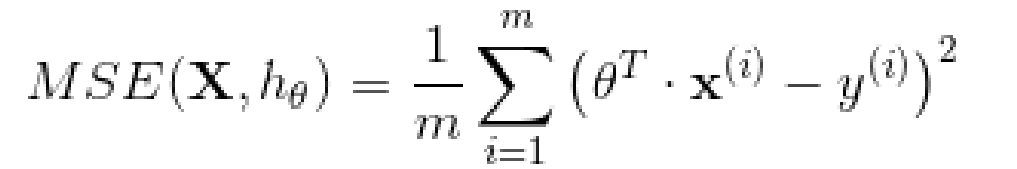
四、正規方程
為了找到最小化損失函數的 值,可以采用公式解,換句話說,就是可以通過解正規方程直接得到最后的結果。正規方程如下:
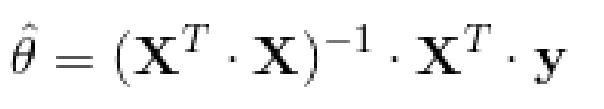
五、示例
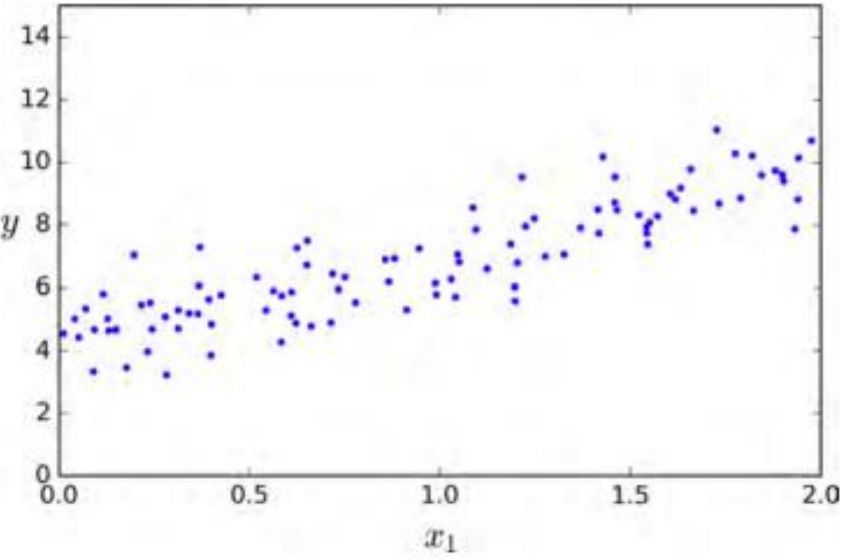
生成一些近似線性的數據來測試一下這個方程。
importnumpyasnpX=2*np.random.rand(100,1)y=4+3*X+np.random.randn(100,1)
X_b=np.c_[np.ones((100,1)),X]theta_best=np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
實際上產生數據的兩個系數是4和3 。讓我們看一下最后的計算結果。
>>>theta_bestarray([[4.21509616],[2.77011339]])
由于存在噪聲,參數不可能達到到原始函數的值。現在我們能夠使用 來進行預測:
X_new=np.array([[0],[2]])X_new_b=np.c_[np.ones((2,1)),X_new]y_predict=X_new_b.dot(theta_best)y_predict>>>array([[4.21509616],[9.75532293]])
六、模型圖像
plt.plot(X_new,y_predict,"r-")plt.plot(X,y,"b.")plt.axis([0,2,0,15])plt.show()
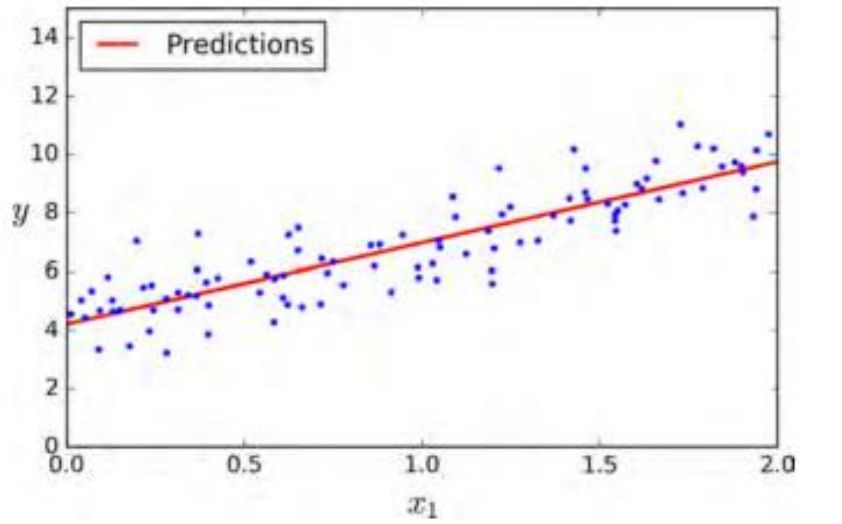
使用下面的 Scikit-Learn 代碼可以達到相同的效果:
fromsklearn.linear_modelimportLinearRegressionlin_reg=LinearRegression()lin_reg.fit(X,y)lin_reg.intercept_,lin_reg.coef_(array([4.21509616]),array([2.77011339]))lin_reg.predict(X_new)array([[4.21509616],[9.75532293]])
七、梯度下降
梯度下降是一種非常通用的優化算法,它能夠很好地解決一系列問題。梯度下降的整體思路是通過的迭代來逐漸調整參數使得損失函數達到最小值。假設濃霧下,你迷失在了大山中,你只能感受到自己腳下的坡度。為了最快到達山底,一個最好的方法就是沿著坡度最陡的地方下山。這其實就是梯度下降所做的:它計算誤差函數關于參數向量 的局部梯度,同時它沿著梯度下降的方向進行下一次迭代。當梯度值為零的時候,就達到了誤差函數最小值 。具體來說,開始時,需要選定一個隨機的 (這個值稱為隨機初始值),然后逐漸去改進它,每一次變化一小步,每一步都試著降低損失函數(例如:均方差損失函數),直到算法收斂到一個最小值。在梯度下降中一個重要的參數是步長,超參數學習率的值決定了步長的大小。如果學習率太小,必須經過多次迭代,算法才能收斂,這是非常耗時的。另一方面,如果學習率太大,你將跳過最低點,到達山谷的另一面,可能下一次的值比上一次還要大。這可能使的算法是發散的,函數值變得越來越大,永遠不可能找到一個好的答案。最后,并不是所有的損失函數看起來都像一個規則的碗。它們可能是洞,山脊,高原和各種不規則的地形,使它們收斂到最小值非常的困難。梯度下降的兩個主要挑戰:如果隨機初始值選在了圖像的左側,則它將收斂到局部最小值,這個值要比全局最小值要大。 如果它從右側開始,那么跨越高原將需要很長時間,如果你早早地結束訓練,你將永遠到不了全局最小值。
八、梯度下降的陷阱
幸運的是線性回歸模型的均方差損失函數是一個凸函數,這意味著如果你選擇曲線上的任意兩點,它們的連線段不會與曲線發生交叉(譯者注:該線段不會與曲線有第三個交點)。這意味著這個損失函數沒有局部最小值,僅僅只有一個全局最小值。同時它也是一個斜率不能突變的連續函數。這兩個因素導致了一個好的結果: 梯度下降可以無限接近全局最小值。(只要你訓練時間足夠長,同時學習率不是太大 )。
-
梯度
+關注
關注
0文章
30瀏覽量
10485 -
線性回歸
+關注
關注
0文章
41瀏覽量
4429 -
訓練模型
+關注
關注
1文章
37瀏覽量
3953
原文標題:訓練模型
文章出處:【微信號:lccrunfly,微信公眾號:Python機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
Pytorch模型訓練實用PDF教程【中文】
探索一種降低ViT模型訓練成本的方法
微軟在ICML 2019上提出了一個全新的通用預訓練方法MASS

新的預訓練方法——MASS!MASS預訓練幾大優勢!

一種側重于學習情感特征的預訓練方法

融合Image-Text和Image-Label兩種數據的多模態訓練新方式
介紹幾篇EMNLP'22的語言模型訓練方法優化工作
基于生成模型的預訓練方法

混合專家模型 (MoE)核心組件和訓練方法介紹





 訓練模型:討論兩種訓練方法
訓練模型:討論兩種訓練方法












評論