離散傅里葉變換的應用之一——用FFT分析信號頻譜

題目如下：

欲解此題，關鍵掌握以下幾點：

第一，分清“截取數據長度”（即窗函數長度）與“DFT點數”二者的不同；

第二，能夠根據模擬頻率推斷出DFT譜峰處對應的序號k的數值，方法如下：

首先，由模擬頻率轉換為數字域頻率：

圖1

然后，數字域頻率對應到DFT的序號k

圖2

綜合以上兩式，得到：

圖3

【題目分析與解答】

我們按照DFT分析信號頻譜的三個步驟來分別求解：

第一步：采樣。所以首先，我們寫出采樣后離散時間信號的表達式：

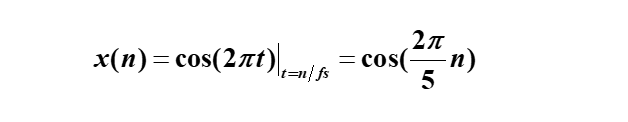
其周期為10。

第二步：時域加窗（即截取）

截取10點長，相當于將該周期信號x(n)與10點長的矩形窗相乘，得到v(n)，所以我們求v(n)的DTFT。

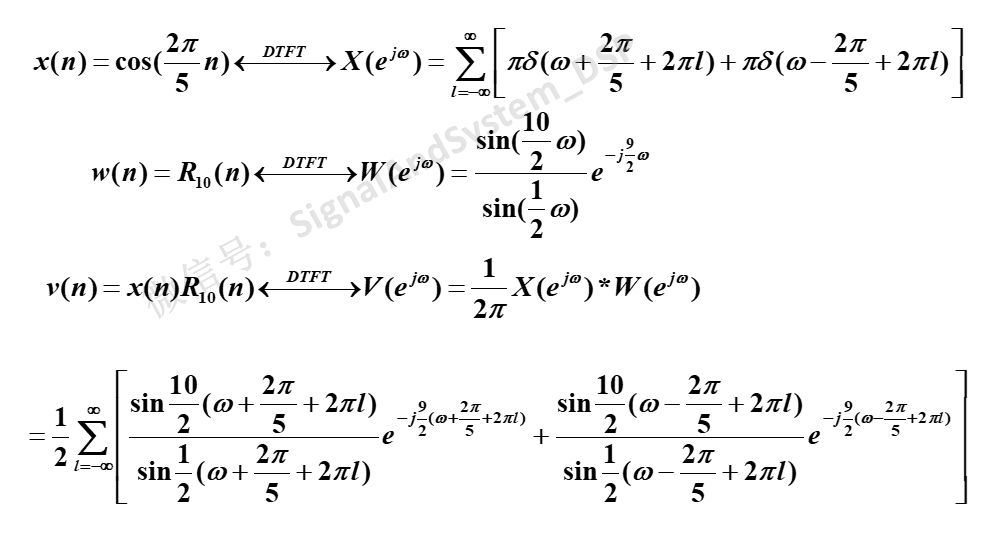
圖4

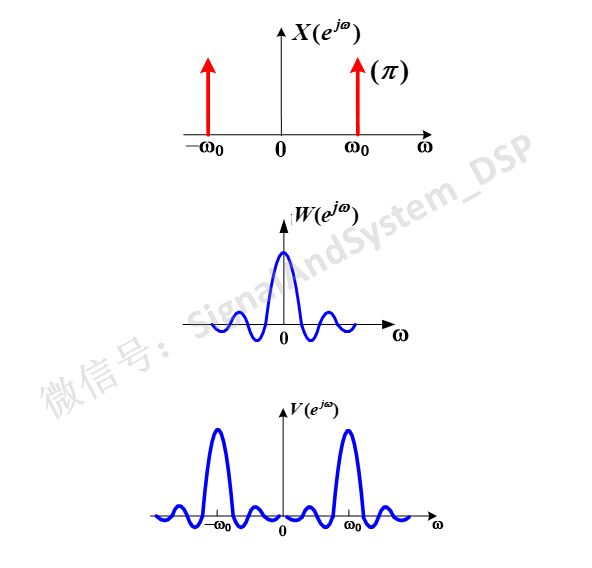
圖5

注意，上圖中只畫出了[-Π，Π] 區間的圖形，實際上DTFT是以2Π為周期的（所以嚇人的公式中有西格瑪求和符號）。

第三步：頻域抽樣，也就是對V(e^jw)在 [0，2Π] 區間抽取N個點（N為DFT點數，而非第二步中截取的長度）

再次把狐假虎威的公式擺出來（因為有些同學有強迫癥，非要看看公式長什么樣，注意，要先把圖4中的V(e^jw)的西格瑪求和符號去掉，只取0~2Π區間的，所以，后面一項是w-2Π/5+2Π，也就是w+8Π/5，然后再把w變成2Πk/N）（在4月28日發的文章中，下面這個公式寫錯了，沒有人給我提出來。看來你們都沒仔細看公式。）

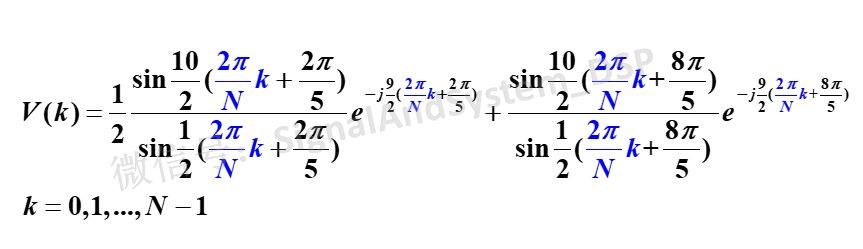
圖6

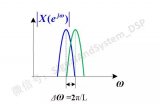
其實V(k) 就是下圖中的紅點點啦。

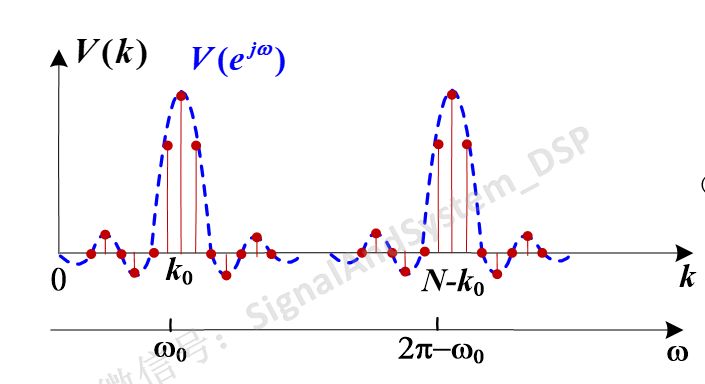
圖7

好了，那么最后的問題就是，N取不同值時（也就是做不同點數的DFT）這些紅點點顯然也不同。對于此題來說，這三種N的取值（10、20、128）得到的結果到底是什么呢？

你看到或者聽到這里的話，暫停一下，自己算算唄。

我直接把matlab畫圖的結果給出來。

用前面的公式算一下：f=kfs/N，最后那個128點DFT的圖，最高的譜峰序號k是多少？

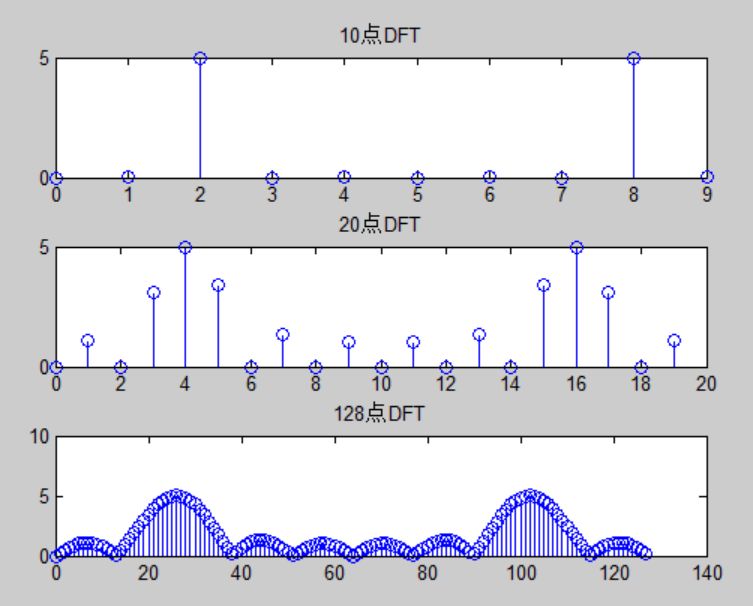
圖8

最后附上matlab程序。

clc;clear all;

f0=1;fs=5;%單位：Hz

n=0:1000;L=10;

xn=cos(2*pi*f0*n/fs);%時域離散時間信號

Xk1=fft(xn(1:L),10);

Xk2=fft(xn(1:L),20);

Xk3=fft(xn(1:L),128);

subplot(311);stem((0:length(Xk1)-1),abs(Xk1));title('10點DFT');

subplot(312);stem((0:length(Xk2)-1),abs(Xk2));title('20點DFT');

subplot(313);stem((0:length(Xk3)-1),abs(Xk3));title('128點DFT');

下面分析一下：

首先看N=10時，此時的結果看似最為干凈清爽，只有干干凈凈兩根線。但有的同學要問了，單頻信號，只有一個頻率成分，應該只有一根譜線呀？為什么會有兩根？

我們先看第一根，k=2那個譜線，對應頻率為2*fs/10=2*5/10=1Hz，與題設cos（2Πt）完全吻合。k=8那根譜線是怎么一回事呢？是負頻率周期延拓過去的，本來在-2，-2+10就等于8了。所以，（敲黑板，以下結論很重要）

對實信號做N點DFT，我們只需要看前N/2根譜線就行了，不用關注N/2~N-1之間的。

再看N=20和N=128的DFT結果，怎么出來那么多根譜線呢？

回過頭去看一看，做DFT之前的截取L點長的序列cos(2Πn/5)的頻譜到底是什么樣子呢？是圖7中的虛線所示。而N點DFT，是對V(e^jw)在 [0，2Π] 區間抽取N個點。相當于把連續的頻譜圖（V(e^jw)，如圖7中的虛線所示），用一張不透明的紙蓋住，紙上以2Π/N為間隔開了一些縫，露出來的點才是我們得到的DFT的結果。這就是頻域抽樣產生的”柵欄效應“。

所以，不管是10點DFT干干凈凈的兩根線，還是128點DFT密密麻麻的那么多根線，背后隱藏的，都是連續的頻譜函數。之所以10點DFT的結果看起來更順眼，無非是因為因為2Π/N也恰好是旁瓣的寬度（因為信號的周期和截取長度也是10）

在DFT譜分析中，當DFT點數N大于數據本身的實際點數L時，相當于在數據后面補上了L-N個0再做DFT，稱為“補零DFT“。補零經常是必要的，補零相當于對信號頻譜以更小的間隔采樣，得到更多的頻譜的信息。而且有時數據長度不是2的整數次冪，如果我們想采用基2FFT算法，就必須進行補零。

此題以單頻周期信號為例，展示了不同點數DFT時結果的不同。給人一種錯覺：補零，似乎沒帶來任何好處，反倒是點數最少的10點DFT的結果最好看。

是不是這樣呢？當然了，如果你知道這個周期信號的周期是多少，毫無疑問，就截取一個周期的數據，做同樣點數的DFT，結果最好看。但在分析實際問題時，要么信號根本沒有周期性；要么雖然有周期性，但你不知道；而且實際信號也不會是簡單的單頻信號，會包含多個頻率分量。這個時候，在系統性能、實時性、存儲量等等容許的范圍內，截取盡量長的數據（即獲取更多的信息，得到更高的頻率分辨率，下一篇會專門講頻率分辨率），做盡量多點數的DFT（即對頻譜進行更為精細的采樣）。

而且，實際應用中，由于DFT的點數一般都比較大，我們一般不會以離散的形式畫頻譜圖，而是直接將頻譜圖化成連續的曲線。例如，上例中，我們截取128點長的數據，做128點DFT，用連續曲線形式畫圖（matlab中為plot函數），并且只畫出前一半（即0~N/2-1）的點，并且把橫軸直接轉換為Hz，如下圖所示：

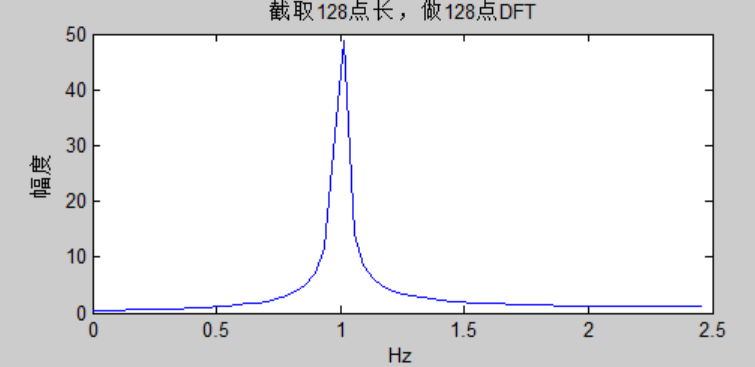
Matlab代碼如下：

上圖中，橫軸單位為：Hz。采用如下公式，將序號k轉換為模擬頻率Hz：

DFT分析信號頻譜，是實際中應用最廣泛的數字信號處理算法，還有很多種題目可以出。還是那句話，題目無窮無盡，而原理就那么多，大家只有掌握了其真正含義，才能以不變應萬變。