Thevenin定理是一種分析方法，用于將復雜電路轉換為簡單的等效電路，該電路由與電源電壓串聯的單個電阻組成

在前三個教程中，我們研究過使用基爾霍夫電路定律，網格分析和最后的節點分析來解決復雜的電路。但是還有更多的“電路分析定理”可供選擇，可以計算電路中任何一點的電流和電壓。在本教程中，我們將看一個已經開發的更常見的電路分析定理（Kirchhoff的定理），Thevenin定理。

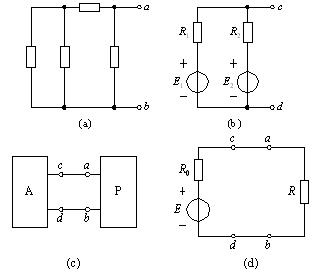
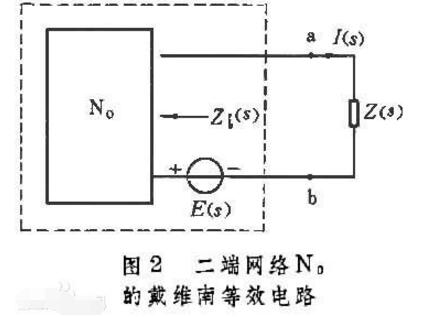
Thevenin定理聲明“任何包含多個電壓和電阻的線性電路都可以用一個單獨的電壓串聯，單個電阻連接在負載上”。換句話說，無論多么復雜，都可以將任何電路簡化為等效的雙端電路，只需一個恒定電壓源與一個連接到負載的電阻（或阻抗）串聯，如下所示。 / p>

戴維南定理在電源或電池系統和其他互連電阻電路的電路分析中特別有用，它會對電路的相鄰部分產生影響。

Thevenin的等效電路

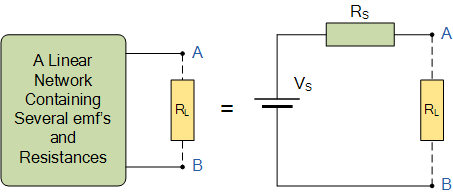
負載電阻 R L ，任何由多個電阻電路元件和能源組成的復雜“單端口”網絡都可以用一個等效電阻 Rs 和一個等效電壓 Vs的 。 Rs 是回溯到電路的源電阻值， Vs 是端子上的開路電壓。

例如，考慮電路來自上一節。

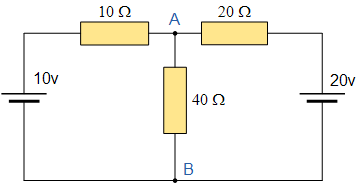
首先，要分析電路，我們必須移除中心40Ω負載電阻連接在端子 AB 上，并去除與電壓源相關的任何內部電阻。這是通過將連接到電路的所有電壓源短路來實現的，即 v = 0 ，或者打開任何連接的電流源，使 i = 0 。這樣做的原因是我們希望有一個理想的電壓源或理想的電流源用于電路分析。

通過計算得到等效電阻 Rs 的值從端子 A 和 B 回顧的總電阻，所有電壓源都短路。然后我們得到以下電路。

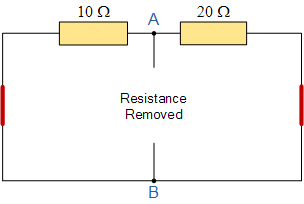
找到等效電阻（Rs）

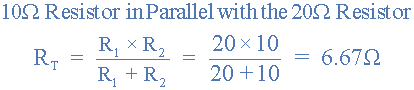
電壓 Vs 定義為端子 A 和 B 當它們之間存在開路時。即沒有連接負載電阻 R L 。

找到等效電壓（Vs）

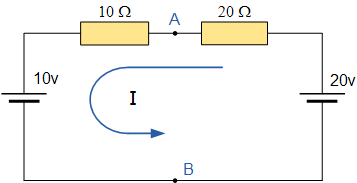
我們現在需要將兩個電壓重新連接回電路，并且 V S = V AB 在環路中流動的電流計算如下：

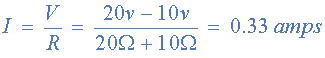
這兩個電阻的電流為0.33安培（330mA），因此20Ω電阻或10Ω電阻上的電壓降可以計算為：

<跨度> V <子> AB = 20-（20Ωx0.33amps）= 13.33volts。

或

V AB = 10 +（10Ωx0.33amps）= 13.33volts ，相同。

然后戴維寧的等效電路將包括6.67Ω的串聯電阻和 13.33v 的電壓源。將40Ω電阻連接回電路后，我們得到：

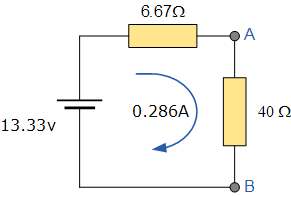
來自這個在電路周圍流動的電流如下：

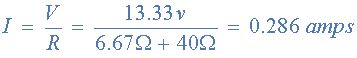
這又是 0.286amps 的相同值我們在前面的電路分析教程中發現了使用基爾霍夫電路定律。

戴維寧定理可以作為另一種電路分析方法使用，在復雜電路的分析中特別有用。由一個或多個電壓或電流源和電阻組成，以通常的并聯和串聯連接排列。

雖然戴維南的電路定理可以用電流和電壓進行數學描述，但它不如大型網絡中的網格電流分析或節點電壓分析，因為在任何戴維寧練習中通常都需要使用網格或節點分析，所以它也可以從一開始就使用。然而，戴維寧的晶體管，電池等電壓源的等效電路在電路設計中非常有用。

戴維南定理概要

我們在這里看到戴維寧定理是另一種類型的電路分析工具，可用于將任何復雜的電氣網絡簡化為由單個電壓源組成的簡單電路， Vs 與單個電阻串聯， Rs 。

當從端子 A 和 B 回顧時，該單個電路的行為方式與它所取代的復雜電路完全相同。這就是 AB 終端的 iv 關系是相同的。

使用Thevenin定理解決電路的基本步驟是如下：

1。移除負載電阻 R L 或相關組件。

2.通過短接所有電壓源或開路所有電流源，找到 R S 。

3.通過常用的電路分析方法找到 V S 。

4。找到流過負載電阻 R L 的電流。

在下一個教程中，我們將看看諾頓定理這允許由線性電阻和源組成的網絡由等效電路表示，其中單個電流源與單個源電阻并聯。