1 引言
??? 眾所周知，普通異步電動機的起動轉矩小，起動電流大。這使得它在某些場合的應用受到了限制。為了改善普通感應電機的起動性能，許多學者進行了有意義的研究。先后提出了雙鼠籠電機，轉子采用刀形、凸形槽等方法來提高電機的起動轉矩。20世紀初國外學者提出了實心轉子異步電動機，它具有高起動轉矩和低起動電流的特點，但其效率和功率因數(shù)較差。為了既有起動轉矩大、起動電流小的特點；又兼顧效率和功率因數(shù)高，我們提出了復合籠條轉子異步電動機。本文基于交流電機理論仿真分析了這種電機起動性能，并研究了轉子槽內材料磁導率和電阻率的變化對這種電機起動性能的影響。
2 復合籠條異步電動機的仿真數(shù)學模型
2.1 復合籠條轉子異步電動機的特點
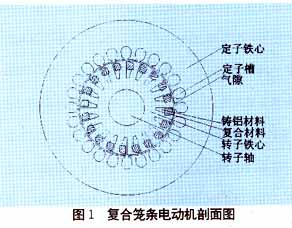
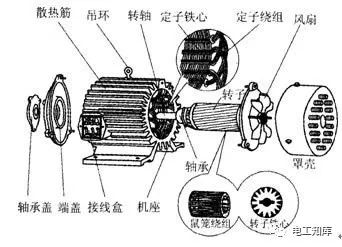
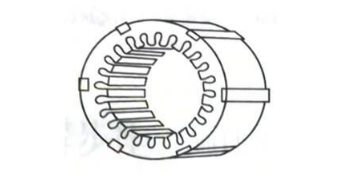
??? 復合籠條轉子異步電動機定子結構、電磁關系與普通籠型感應電動機相同，所不同的是它的轉子結構。電機的剖面圖如圖1所示。復合籠條轉子采用雙鼠籠結構，上層籠采用高電阻率材料，該復合材料是用一定比例的銅鐵合金材料構成，下層籠采用鑄鋁材料，端部是由鋁構成端部回路。采用這種復合材料制成的上層籠條，可通過改變電阻率ρ和磁導率μ而改變起動轉矩和起動電流的大小。

2.2 復合籠條轉子感應電動機的數(shù)學模型
??? 根據(jù)文獻，在不計鐵心飽和，忽略諧波磁勢影響，氣隙均勻的情況下，復合籠條轉子異步電動機的基本方程為：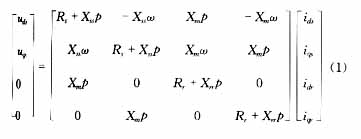

式中：下標s,r分別代表定子、轉子各分量；
??? 下標d,q分別代表d,q,0坐標系下的量；
? ?X_ss為定子自電感；
??????? X_rr為轉子自電感；
??????? X_m為定轉子間互感；
??????? R_s為定子電阻；
??????? R_r為轉子電阻；
??????? p為微分算子；
??? ω為轉子角速度；
??????? i為電流；
??????? u為電壓。
??? 定子自感X_ss＝Ｘ_m＋Ｘ_１σ，轉子自電感X_rr＝Ｘ_m＋Ｘ_２σ，Ｘ_１σ和Ｘ_２σ分別為定轉子漏感。
??? 式(1)可改寫成狀態(tài)方程的形式并簡記為：

??? 其中I為電流矩陣；X為電感矩陣；U為電壓矩陣；R為電阻矩陣；G為與旋轉電勢有關的電感矩陣。
??? 復合籠條轉子異步電動機轉子運動方程為：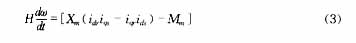

式中：H為轉動慣量；
??? ?M_m為機械負載轉矩；
將式(2)、(3)合并起來即得復合籠條轉子異步電動機的狀態(tài)方程。記為：

式中：u為輸入電壓矩陣；
??? ?t為連續(xù)時間。
3 仿真分析
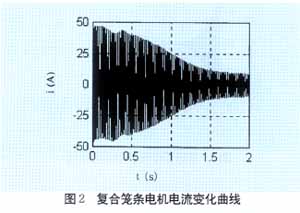
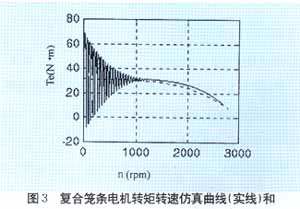
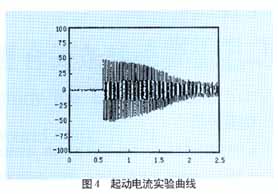
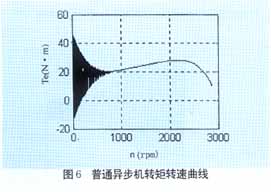
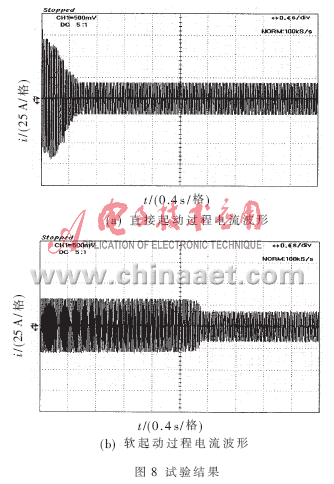
??? 為了研究復合籠條轉子異步電動機的起動性能，我們制造了一臺3KW的該電動機。對其進行了實驗，得到了該電機實測參數(shù)和起動時電流曲線、轉速轉矩曲線。電機的實測參數(shù)為p=3KW,I_st＝３１．２，Ｔ_est＝２４Ｎ．m,cosΦ＝０．８１，η＝７８．５％。給該電機加380V，50Hz的額定電壓，帶額定負載，利用建立的數(shù)學模型對該電機起動過程進行了仿真，得到了起動時電流變化曲線如圖2所示和轉矩轉速曲線如圖3所示，并與實驗曲線進行了比較，說明了仿真的正確性。實驗電流曲線如圖4所示，轉矩轉速曲線如圖3中的虛線。圖5，圖6給出了普通3KW、2極感應電動機的起動電流變化曲線和轉矩轉速變化曲線，與圖2，3比較，可得知復合籠條感應電動機具有良好的起動性能。

4 轉子材料對復合籠條感應電動機起動特性的影響
4.1 轉子籠條電阻率的影響
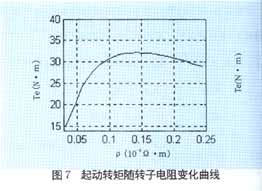
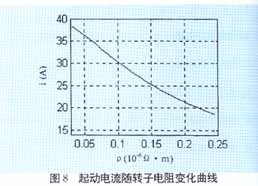
??? 根據(jù)電機設計的知識，通過不同轉子電阻下的仿真結果，可以得到起動轉矩隨籠條電阻率的變化曲線(如圖7所示)和電流隨轉子電阻率的變化曲線(如圖8所示)。一般認為電阻率增大，起動轉矩增大。但從曲線可以看出當轉子電阻率增大到一定范圍時，轉矩隨轉子電阻率的增大反而減小。從仿真結果知，轉子電阻率增大，起動時間加長，故轉子電阻率增大并不一定對起動有利。

4.2 轉子籠條磁導率的影響
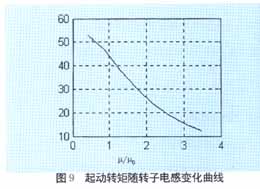
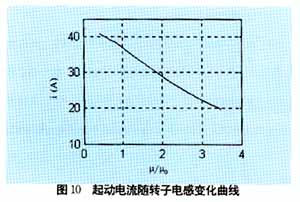
??? 根據(jù)電機設計的知識，通過不同轉子漏抗下的仿真結果得到了起動轉矩隨轉子籠條磁導率變化曲線(如圖9所示)、起動電流隨籠條磁導率變化曲線(如圖10所示)。可以看出隨磁導率的增加，起動轉矩和起動電流都在減小，為了獲得較小的起動電流可以增大磁導率，但必然減小起動轉矩，所以在設計電機時，應根據(jù)設計要求選擇兩者的最佳結合點。磁導率越大，電機起動時間越長，當磁導率大到一定時，由于轉矩減小，電機將無法起動。

5 結論
??????? (1)采用復合籠條的異步電動機比采用鑄鋁籠條的起動轉矩大，起動電流小。
??????? (2)起動電流隨籠條電阻率的增大而減小，當電阻率為鑄鋁電阻率的約3.5倍時，起動轉矩最大。
??????? (3)起動轉矩和電流隨籠條磁導率的增大基本按線性減小。

參考文獻：

［１］D.C.White,H.H.Woodson.Electromechanical Energy Conversion［Ｍ］.Wiley Sons,1959
［２］C.M.Ong“Dynamic simulation of electric machinery using Matlab/Simulink”［Ｓ］．Ed.Mc GrawHill.1998,New Jersey pp.202-204
［３］J.Appelbaum,I.A.Khan,and E.F.Fuchs,“Optimization of three_phase induction motor design.Pt Ⅱ:The efficiency and Cost of an option design”［Ｊ］.IEEE Trans.On Energy Conversion Vol.Ec-2,1987,pp.145-422
［４］R.Ramarathman and B.G.Desai,“Optimization of polyphase induction motordesign_A nonlinear programming approach”［Ｊ］．IEEE trans.On Power Apparatus and Systems.Vol PAS-80,1971,pp.570-578