本文主要介紹利用FPGA的自身的特性實現隨機數發生器，在Virtex-II Pro開發板上用ChipScope觀察隨機數序列，以及在PCIe4Base（基于Virtex-4 FPGA）上實現。

基本的原理

隨機數在計算機科學中的密碼學中有著重要的用途，常常被用作密鑰的來源。隨機數包括偽隨機數以及真隨機數。偽隨機數是通過一定的算法計算得出，具有類似于隨機數的統計特征，這樣的發生器稱為偽隨機數發生器。而真隨機數是通過物理現象產生，例如使用電子元件的噪聲、核裂變等等作為噪聲源[2],這樣的隨機數發生器叫做物理隨機數發生器，也叫做真隨機數發生器（TRNG：Ture Random Number Generator）。

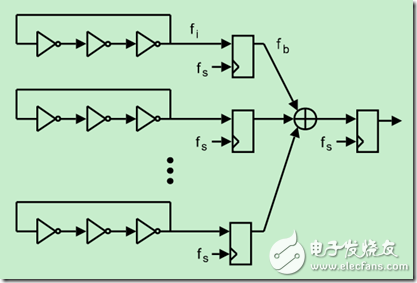
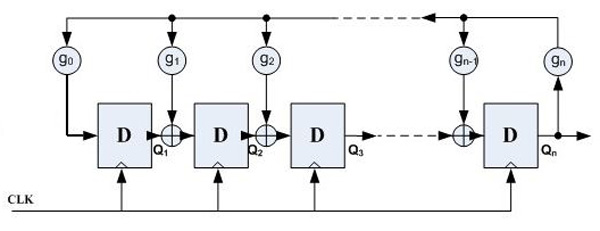
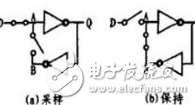
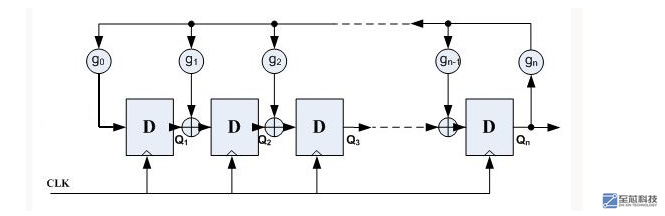
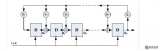
基于FPGA的隨機數發生器基本原理是利用奇數個反相器組成振蕩器作為隨機數發生器的噪聲源，因為由于FPGA自身的特性--信號傳輸存在抖動，所以多個反相器組成振蕩器輸出也不是很穩定的時鐘信號，每個振蕩器輸出不是相同的，這樣成為了理想的噪聲源，見圖1。振蕩器輸出通過D觸發器進行采樣輸出，采樣頻率是fs，然后多個采樣輸出結果經過異或門之后再通過一個D觸發器進行采樣，采樣頻率還是fs。這樣簡單的隨機數發生器就完成了。

實現

根據前面所述的原理圖，進行如下設計：抽樣頻率是fs為50MHz，用3個反相器組成一個振蕩器，共用了25個振蕩器。因為整個結構很簡單，這里就不多講述，主要想說的是振蕩器的描述。為了避免綜合器將振蕩器進行一定的優化從而背離當初的設計，所以在代碼中添加了屬性語句，用于保證網絡不被優化掉。見28至31行，36至39行。

1: library IEEE;
2: use IEEE.STD_LOGIC_1164.ALL;
3: use IEEE.STD_LOGIC_ARITH.ALL;
4: use IEEE.STD_LOGIC_UNSIGNED.ALL;
5: ---- Uncomment the following library declaration if instantiating
6: ---- any Xilinx primitives in this code.
7: library UNISIM;
8: use UNISIM.VComponents.all;
9:
10: entity Ring_osc_3 is
11: port ( clk : in STD_LOGIC;
12: D_out : out STD_LOGIC
13: );
14: end Ring_osc_3;
15:
16: architecture Behavioral of Ring_osc_3 is
17: ---------------------------------------
18: -- Interial signal in the Ring_OSC
19: ---------------------------------------
20: signal delay1 : std_logic;
21: signal delay2 : std_logic;
22: signal delay3 : std_logic;
23:
24: ---------------------------------------------------------------------
25: --Attributes to stop delay logic from being optimised.
26: ---------------------------------------------------------------------
27: attribute keep : string;
28: attribute keep of delay1 :signal is "true";
29: attribute keep of delay2 :signal is "true";
30: attribute keep of delay3 :signal is "true";
31:
32: ---------------------------------------------------------------------
33: --Attributes to stop trim logic from being optimised
34: ---------------------------------------------------------------------
35: attribute s : string;
36: attribute s of delay1 : signal is "true";
37: attribute s of delay2 : signal is "true";
38: attribute s of delay3 : signal is "true";
39: 40: ---------------------------------------
41: --Code start
42: ---------------------------------------
43:
44: begin
45: --osc_out is the last invertor output,
46: --and also the output feeds back to the first invertor
47: --invertor 1
48: inv_lut1: LUT1
49: generic map (init => X"1")
50: port map (
51: I0 => delay1,
52: O => delay2);
53:
54: --invertor 2
55: inv_lut2: LUT1
56: generic map (init => X"1")
57: port map (
58: I0 => delay2,
59: O => delay3);
60:
61: --invertor 3
62: inv_lut3: LUT1
63: generic map (init => X"1")
64: port map (
65: I0 => delay3,
66: O => delay1);
67:
68: --D Flip-flop
69: D_ff : FD
70: port map (
71: D => delay3,
72: Q => D_out,
73: C => clk);
74:
75: end Behavioral;
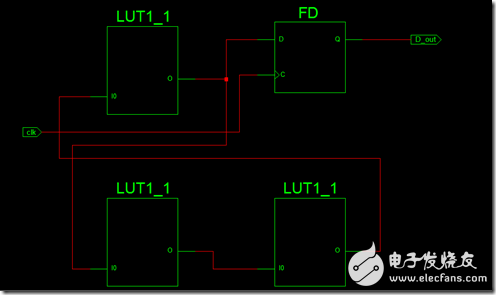
振蕩器最后綜合出來的結果是（圖2）：

ChipScope的觀察

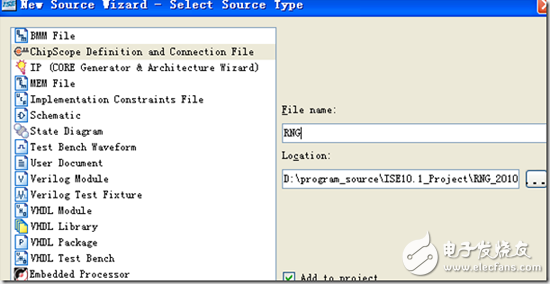
首先對管腳以及時鐘進行約束，為了通過ChipScope觀察隨機數的輸出序列，還需要添加ICON以及ILA IP core。操作如下，在ISE窗口左側的source欄中右鍵選擇new source，然后見到New Source Wizard窗口。輸入一個名字，然后點擊OK。然后在Source窗口中看到生成的cdc source file。接下來就是配置觸發信號、觀察信號、時鐘信號等屬性。

?

這里不細說如何配置，具體見參考文獻3。

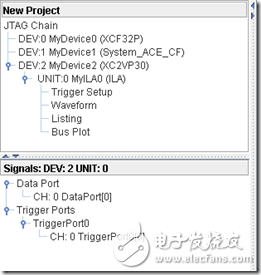
在這里，觀察的RNG輸出信號同時作為觸發信號來配置。配置完后編譯實現。然后再Process欄中選擇Analyze Design Using ChipScope 同時連接Virtex-II Pro板子并且上電。進入ChipScope　Pro Analyzer界面后點擊工具欄中的OPEN Cable/Search JTAG Chain，然后看到JTAG Chain上的三個設備。右鍵選中FPGA芯片（XC2VP30），選擇配置，選中剛才生成的bit文件。配置完成后會出現圖5的信號列表。
圖5中Trigger Setup是觸發配置，Waveform 是波形列表。

?

?

?

雙擊 Waveform打開波形觀察窗口，因為觸發信號就是需要觀察的信號，所以這里不用設置觸發。在工具欄中點擊 ，你就可以觀察到隨機數的輸出波形了，圖6。肉眼觀察信號比較隨機，但是沒有定性的測試。
?

隨機數的測試

常用的測試隨機數的工具有ENT[4]，DIEHARD[5]等。而這些工具需要大量的隨機數（最好是10M以上的數據）才可以測試，而用ChipScope最多一次只能才是65536bit的數據，這樣的測試肯定是不行的。所以將同樣的設計放到了PCIeV4base，這個板子具有PCIe插槽，用的是Virtex-4的FPGA芯片。PC機通過PCIe橋接芯片讀取數據，這樣很方便得到大量的隨機數數據。

具體的原理圖，圖7。看起來有些麻煩，涉及到了FIFO，Wishbone上添加從設備，以及Linux下PCIe的編程，幸好相關的東西已經有實例和SDK提供，只要做一些修改就可以了。

?

最后通過軟件得到15MB的數據。然后通過ENT工具進行測試，測試的結果如下：

D:\Document\RNG\ent>ent out
Entropy = 7.999890 bits per byte.

Optimum compression would reduce the size
of this 16777212 byte file by 0 percent.

Chi square distribution for 16777212 samples is 2563.57, and randomly
would exceed this value less than 0.01 percent of the times.

Arithmetic mean value of data bytes is 127.5056 (127.5 = random).
Monte Carlo value for Pi is 3.141033445 (error 0.02 percent).
Serial correlation coefficient is -0.000568 (totally uncorrelated = 0.0).

測試的結果分析，得到隨機數比較理想。