傅里葉變換(fft)matlab程序三
clear all %清除內存所有變量
close all %關閉所有打開的圖形窗口
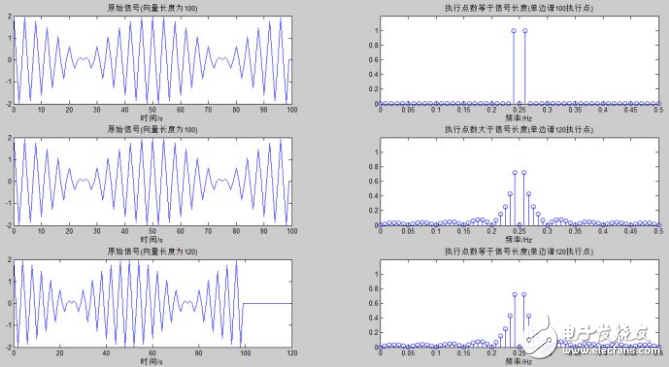
%% 執行FFT點數與原信號長度相等(100點)
% 構建原信號
N=100; % 信號長度(變量@@@@@@@)
Fs=1; % 采樣頻率
dt=1/Fs; % 采樣間隔
t=[0:N-1]*dt; % 時間序列
xn=cos(2*pi*0.24*[0:99])+cos(2*pi*0.26*[0:99]);
xn=[xn,zeros(1,N-100)]; % 原始信號的值序列
subplot(3,2,1) % 變量@@@@@@@
plot(t,xn) % 繪出原始信號
xlabel(‘時間/s’),title(‘原始信號(向量長度為100)’) % 變量@@@@@@@
% FFT分析
NN=N; % 執行100點FFT
XN=fft(xn,NN)/NN; % 共軛復數,具有對稱性
f0=1/(dt*NN); % 基頻
f=[0:ceil((NN-1)/2)]*f0; % 頻率序列
A=abs(XN); % 幅值序列
subplot(3,2,2),stem(f,2*A(1:ceil((NN-1)/2)+1)),xlabel(‘頻率/Hz’) % 繪制頻譜(變量@@@@@@@)
axis([0 0.5 0 1.2]) % 調整坐標范圍
title(‘執行點數等于信號長度(單邊譜100執行點)’); % 變量@@@@@@@
%% 執行FFT點數大于原信號長度
% 構建原信號
N=100; % 信號長度(變量@@@@@@@)
Fs=1; % 采樣頻率
dt=1/Fs; % 采樣間隔
t=[0:N-1]*dt; % 時間序列
xn=cos(2*pi*0.24*[0:99])+cos(2*pi*0.26*[0:99]);
xn=[xn,zeros(1,N-100)]; % 原始信號的值序列
subplot(3,2,3) % 變量@@@@@@@
plot(t,xn) % 繪出原始信號
xlabel(‘時間/s’),title(‘原始信號(向量長度為100)’) % 變量@@@@@@@
% FFT分析
NN=120; % 執行120點FFT(變量@@@@@@@)
XN=fft(xn,NN)/NN; % 共軛復數,具有對稱性
f0=1/(dt*NN); % 基頻
f=[0:ceil((NN-1)/2)]*f0; % 頻率序列
A=abs(XN); % 幅值序列
subplot(3,2,4),stem(f,2*A(1:ceil((NN-1)/2)+1)),xlabel(‘頻率/Hz’) % 繪制頻譜(變量@@@@@@@)
axis([0 0.5 0 1.2]) % 調整坐標范圍
title(‘執行點數大于信號長度(單邊譜120執行點)’); % 變量@@@@@@@
%% 執行FFT點數與原信號長度相等(120點)
% 構建原信號
N=120; % 信號長度(變量@@@@@@@)
Fs=1; % 采樣頻率
dt=1/Fs; % 采樣間隔
t=[0:N-1]*dt; % 時間序列
xn=cos(2*pi*0.24*[0:99])+cos(2*pi*0.26*[0:99]);
xn=[xn,zeros(1,N-100)]; % 原始信號的值序列
subplot(3,2,5) % 變量@@@@@@@
plot(t,xn) % 繪出原始信號
xlabel(‘時間/s’),title(‘原始信號(向量長度為120)’) % 變量@@@@@@@
% FFT分析
NN=120; % 執行120點FFT(變量@@@@@@@)
XN=fft(xn,NN)/NN; % 共軛復數,具有對稱性
f0=1/(dt*NN); % 基頻
f=[0:ceil((NN-1)/2)]*f0; % 頻率序列
A=abs(XN); % 幅值序列
subplot(3,2,6),stem(f,2*A(1:ceil((NN-1)/2)+1)),xlabel(‘頻率/Hz’) % 繪制頻譜(變量@@@@@@@)
axis([0 0.5 0 1.2]) % 調整坐標范圍
title(‘執行點數等于信號長度(單邊譜120執行點)’); % 變量@@@@@@@
結果
 電子發燒友App
電子發燒友App









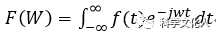









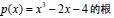










評論