將二進制數視為元胞自動機可能有助于數字二進制計數器的設計和實現嗎?
正如大多數讀者已經知道的那樣,二進制計數類似于任何其他數字系統中的計數。計數從使用下一個可用符號(十進制的 0 到 9,八進制的 0 到 8,十六進制的 0 到 F,二進制的 0 和 1)增量替換最低有效位(最右邊的位置)開始。當這個數字的符號用盡時(因為最后一個符號已經被使用),這個最低有效數字被重置為 0 并且左邊的數字增加。此過程以迭代方式繼續,因此當任何位置的數字符號用盡時,該數字重置為 0,并且其左側的數字遞增。
我們剛剛在上面所做的是設置了一個規則,用于計算或從一個數字演變為下一個數字。一個數字可以被認為是一個n位的一維數組(在二進制的情況下稱為“位”),其中用于一個數字的下一個符號不僅取決于該數字的當前符號,還取決于在數組中其他數字的當前符號上。基于此,我開始懷疑將二進制數視為元胞自動機是否有助于數字二進制計數器的設計和實現。
編者注:從 Conway 的生命游戲到 Langton 的螞蟻再到 Reynold 的 Boids,人工生命模擬展示了由簡單規則引起的復雜緊急行為(另見“人工生命模擬”)。
很明顯,如果不知道元胞自動機是什么以及它如何與數字數組相關,我將無法對此感到疑惑,但是當我們閱讀以下元胞自動機的簡明一般定義時,這種關系變得顯而易見:
一個規則的細胞網格,其特征是有限數量的狀態,這些狀態將根據一些固定規則(進化)從當前變化(進化)到下一代,該規則根據兩者的當前狀態確定每個細胞的新狀態單元格和其他單元格(其鄰域)。
在二進制數的情況下,位等價于單元格,可能的狀態是 0 和 1,自動機是一維的(上面的網格只有一行,因為只有一個數組要考慮),以及任何生成的自動機表示與其所有位的狀態相對應的數字。
一維元胞自動機的一個特例是所謂的初等元胞自動機,其中每個元胞只能有兩個狀態,并且下一代每個元胞的狀態僅取決于元胞及其兩個直接鄰居的當前狀態(右邊和左邊)。這種基本元胞自動機的一個例子就是規則 90,其中所有單元的狀態同時被它們的兩個相鄰單元的狀態的異或 (XOR) 替換。

圖 1:具有隨機初始條件的規則 90 的時空圖(來源:Javier Piay)
當從單個活細胞(只有一個細胞的狀態為 1)開始時,規則 90 具有謝爾賓斯基三角形形式的時空圖(隨時間演變的一維數組)。
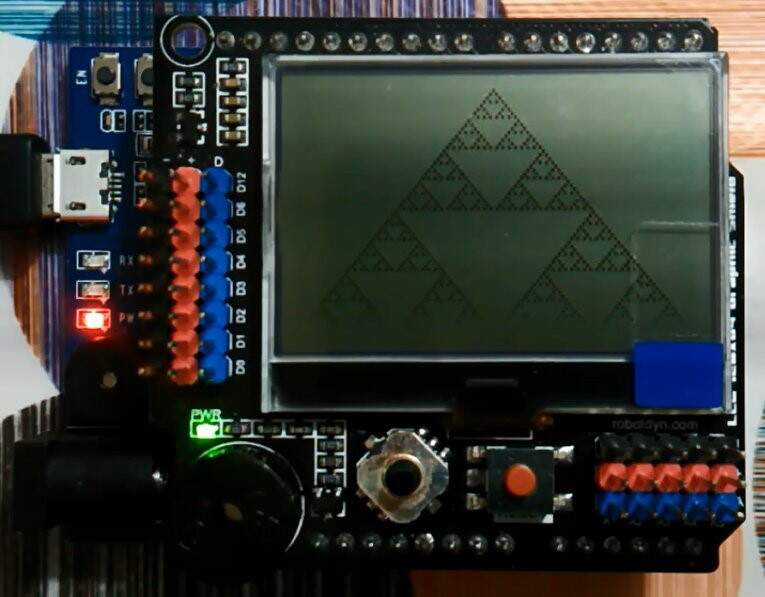
圖 2:規則 90 的時空圖從單個活細胞開始,形成謝爾賓斯基三角形。(來源:哈維爾皮耶)
在本視頻中,您將找到一些我為三個計算機平臺創建的規則 90 自動機動畫:micro:bit、Arduino 和我的SANX-I 微型計算機。
就受歡迎程度和學術/科學興趣而言,約翰康威創造的生命游戲元胞自動機排名第一。康威的生命游戲是一個二維元胞自動機,其中每個細胞根據一些簡單的方法與其八個鄰居相互作用進化規律如下:
任何少于兩個活鄰居的活細胞都會死亡,就像人口不足一樣。
任何有兩三個活鄰居的活細胞都可以活到下一代。
任何有超過三個活鄰居的活細胞都會死亡,就像人口過剩一樣。
任何只有三個活鄰居的死細胞都會變成活細胞,就像通過繁殖一樣。
生命游戲自動機產生許多不同類型的動畫、意想不到和不可預測的模式(如靜物、振蕩器和宇宙飛船),即使是那些偶然發現它的人中最不好奇的人也會對這種細胞自動機著迷。我還編寫了程序來模擬不同平臺上的生命游戲,并從隨機初始配置(生成)和特定配置開始探索這些動畫模式。在此視頻中,您將找到我的 Arduino 生命游戲。
在這個視頻中,你會發現我的 micro:bit 生命游戲:
到目前為止,一切都很好(我希望)。
現在,如果您回想本專欄的開頭,您會記得本文的真正目的是確定將二進制數視為元胞自動機是否有助于數字二進制計數器的設計和實現。我們已經知道,我們正在尋找的元胞自動機將是一維的,但不是基本類型,因為下一代細胞/數字/位的狀態不僅僅取決于細胞的當前狀態及其兩個直接鄰居。實際上,該狀態似乎僅取決于其右側鄰居的當前狀態。你怎么看?
如果你仔細看計數規則,你會發現這是一個迭代過程,其中一個數字的下一個值不僅取決于它自己的值和它右邊數字的值,還取決于數字的值在其右側的數字的右側。這個迭代過程或依賴關系一直持續到數組的最右邊(最低有效位)。換句話說,一個數字的下一個值取決于它自己的值和它右邊所有數字的值。
當我得出這個結論時,我首先認為這樣的自動機會比基本自動機復雜得多(其中一個單元僅受其兩個相鄰鄰居的影響);此外,很難設定和實施進化(計數)規則。幸運的是,我意識到這種對幾個單元格(實際上是右邊的所有單元格)的依賴可以轉換為對右邊相鄰單元格的依賴,從而產生一種“簡化和修改的基本自動機”。
只需向每個單元格(除了其二進制狀態)添加一個新屬性或 FLAG 即可輕松完成此轉換,其值僅由其右側的單元格修改。當其右邊所有單元的狀態為 1 時,該 FLAG 將為 1,這意味著自動機滿足進化規則,因此,單元的下一個狀態將從 0 變為(反轉)為 1,或從 1 到 0,根據本文第一段中描述的增量替換過程(二進制增量)。如前所述,這個FLAG的值只會被右邊的單元格修改;因此,當且僅當此單元狀態的當前狀態值和與右側單元關聯的 FLAG 的值都為 1 時,它將被設置為 1。
如前所述,我稱這個元胞自動機為“簡化的”和“修改的”基本自動機——“簡化”是因為任何單元格(受影響的單元格)的鄰域都被簡化為右側的單元格并被“修改”,因為每個單元格都具有特征不僅取決于它的狀態,還取決于它的 FLAG。
只要一個或多個細胞滿足進化規則(將它們的 FLAG 設置為 1),這個自動機就會進化。但是要讓這個自動機能夠持續進化,最右邊的細胞必須始終滿足進化規則所施加的要求;否則,一旦該單元的狀態變為 0,進化將停止。因此,最右邊的單元將連接到其右側稱為 ENABLE 的外部輸入。如果 ENABLE 為 TRUE(或 1),自動機將進化(執行二進制計數);否則,所有后續世代都將保持不變。
從當前一代到下一代的進化將由從最右邊的單元到最左邊的單元級聯的外部時鐘信號控制。
對于初始或第一代,任何單元格中都允許任何狀態(0/1)。但是,出于演示目的,我們將首先將所有單元格清除為初始狀態 0。
正如你們中最有洞察力的人現在可能意識到的那樣(正如托比魔鬼——羅文·阿特金森爵士扮演的角色——可能會說的那樣),這個自動機可以通過級聯連接來實現,我稱之為“基本單元”。
這個基本單元有兩個輸入和兩個輸出。任何單元的輸入都將連接到其右側鄰居的輸出,而任何單元的輸出將連接到其左側鄰居的輸入。
每個單元的輸入之一將是 CLOCK 信號,另一個將由其右鄰居使用來修改其 FLAG。同樣,每個單元的輸出之一將是 CLOCK 信號,而另一個將用于修改其左側單元的 FLAG。
圖 3 顯示了基本單元的數字電子實現,使用一個 D 型觸發器來存儲其當前狀態,一個 XOR 門在其 FLAG 設置為 1 時更改(反轉)其狀態,以及一個 AND 門來設置當它的狀態和它的 FLAG 都為 1 時,它左邊的單元格的 FLAG 為 1。
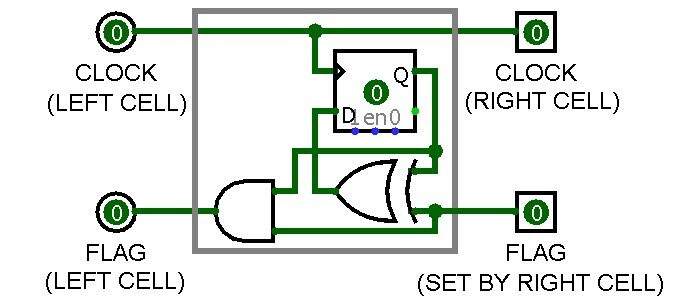
圖 3:自動機基本單元(來源:Javier Piay)
圖 4 顯示了最右邊的基本單元,其輸入連接到外部 CLOCK 和 ENABLE 信號。
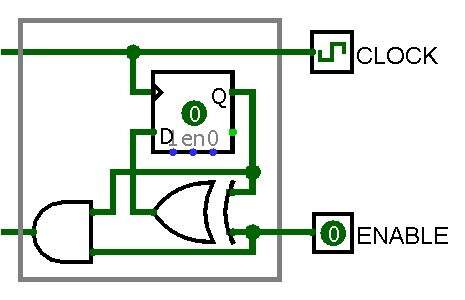
圖 4:Automaton 最右邊的基本單元(來源:Javier Piay)
現在一切都準備就緒,可以互連五個單元,如圖 5 所示:

圖 5:五細胞自動機(來源:Javier Piay)
現在,看看這個視頻,來驗證這個經過簡化和修改的基本元胞自動機實際上是否像一個 5 位二進制計數器一樣進化。
既然我們已經到了本文的結尾,我希望您對這種基于元胞自動機的方法是否有助于二進制計數器的設計和實現有自己的答案。我猜你已經知道我的回答是“是的”(至少,這是給我的)。
如果您的任務是設計和實現這個數字邏輯系統,請不要猶豫,讓我知道您最有可能遵循的其他程序或方法。像往常一樣,我們非常歡迎您的回答、問題或評論。
審核編輯:湯梓紅
 電子發燒友App
電子發燒友App
























評論