如果我們使用的是由模擬方式確定時序的多諧振蕩器,我們將需要考慮組件容差。
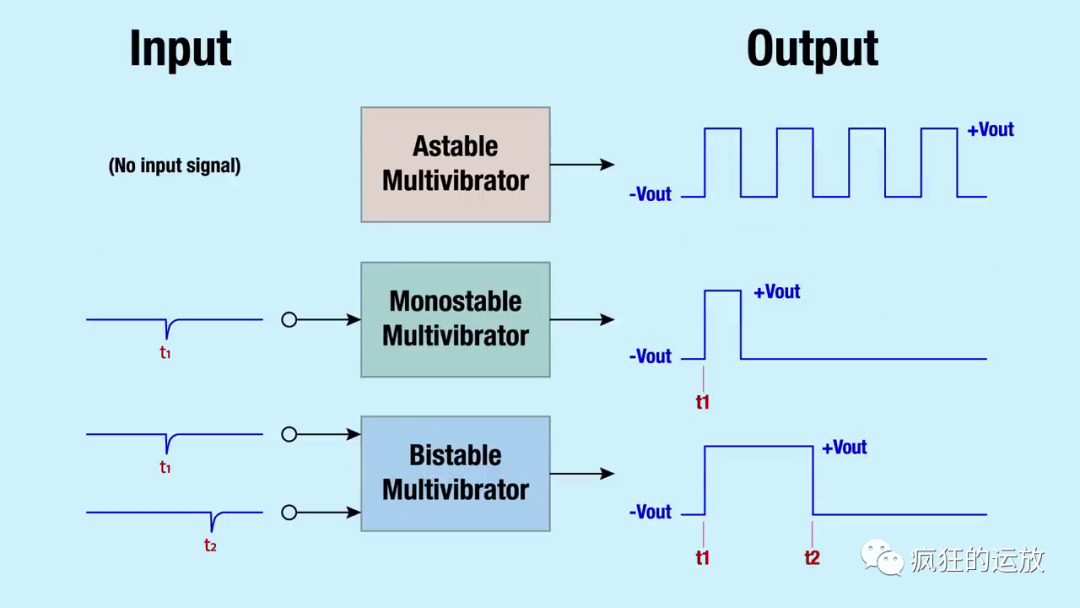
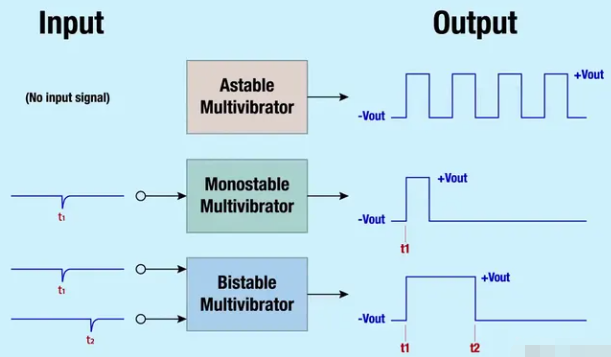
在最近關(guān)于“寄存器與鎖存器與觸發(fā)器”主題的專欄中,我們尊敬的編輯 Max Maxfield 提到了多諧振蕩器(非穩(wěn)態(tài)、單穩(wěn)態(tài)和雙穩(wěn)態(tài)),這引發(fā)了評論部分的一些討論。在這次討論中,一位 EEWeb 社區(qū)成員指出,如果重新觸發(fā)太接近超時,一些可重新觸發(fā)的多諧振蕩器會出現(xiàn)故障。
這很有趣,我想。我已經(jīng)有一段時間沒有使用這些設(shè)備了,所以我決定查看一些數(shù)據(jù)表,看看這種行為是否反映在設(shè)備文檔中。
首先,讓我們看一個不可重新觸發(fā)的單穩(wěn)態(tài)多諧振蕩器。TI 有一個名為CD74HC221的產(chǎn)品,它可以作為一個很好的示例(與往常一樣,我鼓勵您在屏幕上打開我們在這些文章中引用的任何數(shù)據(jù)表或?qū)⑵浯蛴〕鰜恚员隳p松地跟進(jìn))。
數(shù)據(jù)表的第一頁告訴我們,這是一款“帶復(fù)位功能的雙單穩(wěn)態(tài)多諧振蕩器”。該描述解釋了時序由外部電阻器和電容器控制,并且一旦觸發(fā),輸出時序獨立于進(jìn)一步的觸發(fā)輸入,盡管它可以通過復(fù)位控制提前終止。
第 1 頁的真值表告訴我們,Q 輸出通常為低電平,但在輸入 A 的下降沿或輸入 B 的上升沿會產(chǎn)生一個高脈沖(假設(shè)另一個輸入處于正確狀態(tài))。我看了看第 3 頁的邏輯圖。看起來這部分包含幾個 D 型觸發(fā)器和幾個鎖存器。還有幾個運(yùn)算放大器,以及少量晶體管和邏輯門。不過,這個圖有點難以理解,所以讓我們花點時間看看這部分應(yīng)該做什么。
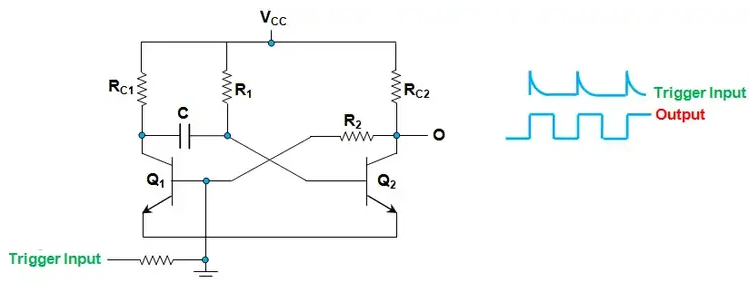
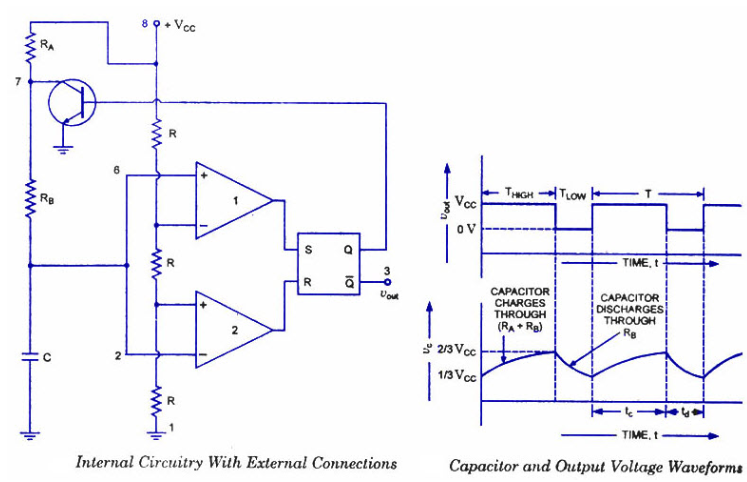
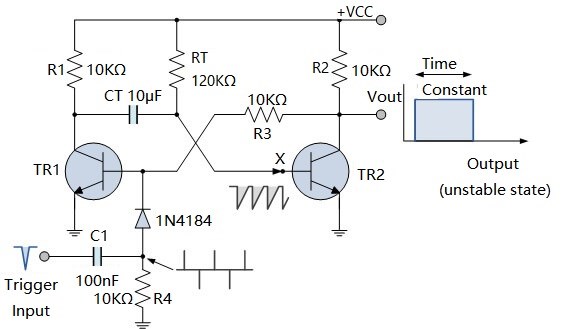
單穩(wěn)態(tài)多諧振蕩器的目的是允許輸入上的短脈沖用于在輸出上產(chǎn)生更長的脈沖。下面的時序圖顯示了它是如何工作的:
請注意,此時序圖未按比例繪制。為了顯示 !A 和 B 上的脈沖,它們必須相對于 RxCx 上的信號被夸大。查看信號 RxCx,我們可以看到它不是數(shù)字信號。觸發(fā)輸入使電容器 C X瞬間放電。釋放時,C X通過電阻器 R X充電。只要 RxCx 低于閾值(此處顯示為 Vth),Q 就會為高。因為這是一個不可重新觸發(fā)的多諧振蕩器,所以當(dāng) Q 為高電平時,邏輯會阻止 RxCx 被拉低(如紅色箭頭所示)。
因為脈沖長度取決于 C X充電的速度,所以它取決于所使用的電阻器 (R X ) 和電容器 (C X ) 的值。在數(shù)據(jù)表的第 1 頁上,我們找到了用于計算脈沖寬度的以下公式:
t W = 0.7* R X * C X在 VCC = 4.5 V
因此,我們可以根據(jù)現(xiàn)有電路中已有的 R X和 C X的值來計算脈沖寬度。或者,我們可以通過為 R X和 C X選擇適當(dāng)?shù)闹祦韯?chuàng)建給定長度的脈沖寬度。
因為找到奇數(shù)值的電阻比找到電容器更容易,所以我們將從選擇一個方便值的電容器開始,然后我們將計算一個相應(yīng)的電阻來給我們所需的脈沖寬度。在選擇 R X和 C X時,我們需要檢查值的限制。我可以在數(shù)據(jù)表中找到的唯一限制是 R X應(yīng)大于 500 Ω。
在查看數(shù)據(jù)表時,我在第 9 頁找到了一些有用的圖表。這些圖表給出了多個 R X值相對于 C X的輸出脈沖寬度,它們?yōu)檫x擇組件值提供了一個有用的起點。
例如,假設(shè)我們想要一個 1 ms 的輸出脈沖寬度,并且我們將在 5 V 下運(yùn)行。從圖 8 中讀取,我們看到 10 3 μs (1 ms)稍微穿過 10K R X線超過 10 5 pF(0.1 μF 或 100 nF)。這意味著,如果我選擇為 C X使用 0.1 μF 電容器,我應(yīng)該得到一個介于 10 kΩ 和 50 kΩ 之間的 R X值。讓我們使用公式來確定值。求解 R X的公式,我們得到:
R X = t W / (0.7 * C X ) = 1 ms / (0.7 * 0.1 μF) = 14.29 kΩ
在我們方便的 1% 電阻表中查找最接近的標(biāo)準(zhǔn)電阻值,我們看到 14.3 kΩ 是一個標(biāo)準(zhǔn)值。這意味著我們的脈沖寬度應(yīng)該非常接近 1 ms。
然而,到目前為止,我們還沒有考慮另一個因素。我們需要考慮到這部分并不是完全數(shù)字化的。事實上,時間是模擬的。因為我們有模擬時序,所以我們需要考慮組件容差。我之前提到過我們將使用 1% 的電阻,但是電容呢?不幸的是,1% 的電容器很難找到并且非常昂貴。另一方面,10% 的電容器比較常見且價格低廉。
這意味著我們的 1 毫秒脈沖會更長或更短,具體取決于電阻器和電容器的確切值。讓我們看看我們的組件公差會產(chǎn)生多大的差異。
一般來說,當(dāng)我們有一個具有公差的組件時,這意味著任何給定零件的實際值 A 將在一個相對于由下式給出的標(biāo)稱值 N 的范圍內(nèi):
N * (1 – tol%) ≤ A ≤ N * (1 + tol%)
使用這個公式,我們的 14.3kΩ、1% 電阻器將介于 14.157kΩ 和 14.443kΩ 之間,而我們的 0.1-μF、10% 電容器將介于 0.09μF 和 0.11μF 之間。現(xiàn)在,當(dāng)我們孤立地討論這些組件時,這些聽起來都不算太糟糕,但是讓我們看看當(dāng)我們將它們組合在一起時會發(fā)生什么:
t W (min) = 0.7 * 14.157 * 0.09 = 0.89 ms
t W(最大值)= 0.7 * 14.443 * 0.11 = 1.11 毫秒
正如我們所看到的,通過將 10% 的電容器與 1% 的電阻器組合在一起,我們最終可能會在脈沖長度上產(chǎn)生 11% 的變化。這只是考慮到容差。如果我們希望該電路在較寬的溫度范圍內(nèi)工作,我們需要考慮這些部件的溫度變化。
再次查看脈沖寬度與電容的關(guān)系圖,看起來這部分可能會有一些變化,具體取決于我們工作的電壓。我沒有在數(shù)據(jù)表中看到這進(jìn)一步量化或解釋,但根據(jù)您需要的準(zhǔn)確度,您可能必須考慮到這一點。
這讓我們回到這是否真的重要。這取決于您說想要 1 毫秒脈沖時的意思。您只是想要一個接近 1 ms 的脈沖、一個至少為 1 ms 的脈沖,還是一個盡可能接近 1 ms 的脈沖?
如果您只想關(guān)閉,那么該電路應(yīng)該足夠好。如果您需要至少 1 毫秒,那么將 R X的值增加11% 左右應(yīng)該可以工作。另一方面,如果你想盡可能接近,你需要一個非常昂貴的電容器,一個電位器來改變 R X的值,或者一個更復(fù)雜的完全數(shù)字電路。
現(xiàn)在,在我被公差分心之前,我在哪里?讓我們繼續(xù)閱讀數(shù)據(jù)手冊,看看還有什么有趣的地方。
DC 電氣規(guī)格與我們在之前的專欄中看到的其他 74HC 系列設(shè)備的規(guī)格相似,因此讓我們繼續(xù)看下一張表,該表標(biāo)題為“開關(guān)功能的先決條件”。在此表中,我們得知輸入有一個最小脈沖寬度以及復(fù)位后的恢復(fù)時間。同樣在此表中,我們提供了不同 R X和 C X值的輸出脈沖寬度。
開關(guān)規(guī)格表包含我們預(yù)期的傳播延遲和轉(zhuǎn)換時間,此外還有“同一封裝中電路之間的脈沖寬度匹配 C X = 1,000 pF,R X = 10 kΩ”參數(shù):
據(jù)此,同一封裝中的兩個單穩(wěn)態(tài)器件之間的脈沖寬度可能相差 2%。盡管沒有明確說明,但我將假設(shè)這是具有相同的 R X和 C X值。我還注意到這是 25°C 時的典型值,因此之前 11% 的容差值現(xiàn)在至少達(dá)到了 13%。
繼續(xù),我們有測試電路和波形,然后在第 9 頁,我們找到了典型的性能曲線。我們已經(jīng)看過脈沖寬度與 C X的關(guān)系圖;現(xiàn)在,讓我們看看這個頁面上的另外兩個圖表:
脈沖寬度與溫度的關(guān)系圖告訴我們,我們可以預(yù)期脈沖寬度會隨著部件變熱而增加。在 25°C 時曲線有相當(dāng)平坦的部分,但如果您希望電路在工業(yè)或軍用溫度范圍內(nèi)運(yùn)行,則需要考慮這種額外的變化。
K 因子與電源電壓的關(guān)系圖有點令人費(fèi)解。首先,他們所說的這個“K 因素”是什么?這是一個很好的問題,因為數(shù)據(jù)手冊中沒有解釋。我猜K是神秘的“0.7”值,我們將R X和C X乘以得到輸出脈沖寬度。如果這是真的,這意味著脈沖寬度隨著電源電壓的降低而增加。我要問的其他問題是:為什么有四行,我使用哪一行?不幸的是,我目前沒有任何關(guān)于這個問題的答案,我非常歡迎您的建議。
在我的下一篇專欄中,我們將介紹可重新觸發(fā)的多諧振蕩器。同時,我歡迎您提出意見、問題和建議。
審核編輯 黃昊宇
 電子發(fā)燒友App
電子發(fā)燒友App























評論