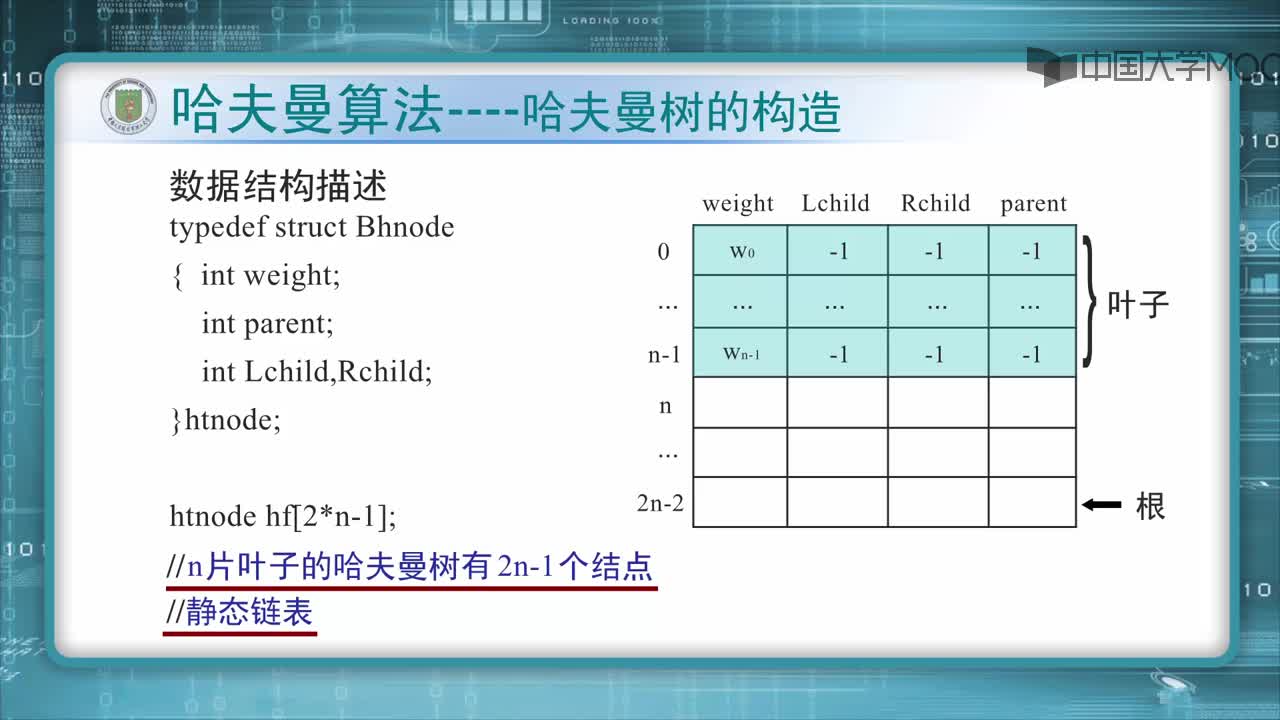
哈夫曼算法原理 - 哈夫曼算法的理解及原理分析,算法實(shí)現(xiàn),構(gòu)造哈夫曼樹的算法

　　哈夫曼算法原理

　　1952年， David A. Huffman提出了一個(gè)不同的算法，這個(gè)算法可以為任何的可能性提供出一個(gè)理想的樹。香農(nóng)-范諾編碼（Shanno-Fano）是從樹的根節(jié)點(diǎn)到葉子節(jié)點(diǎn)所進(jìn)行的的編碼，哈夫曼編碼算法卻是從相反的方向，暨從葉子節(jié)點(diǎn)到根節(jié)點(diǎn)的方向編碼的。

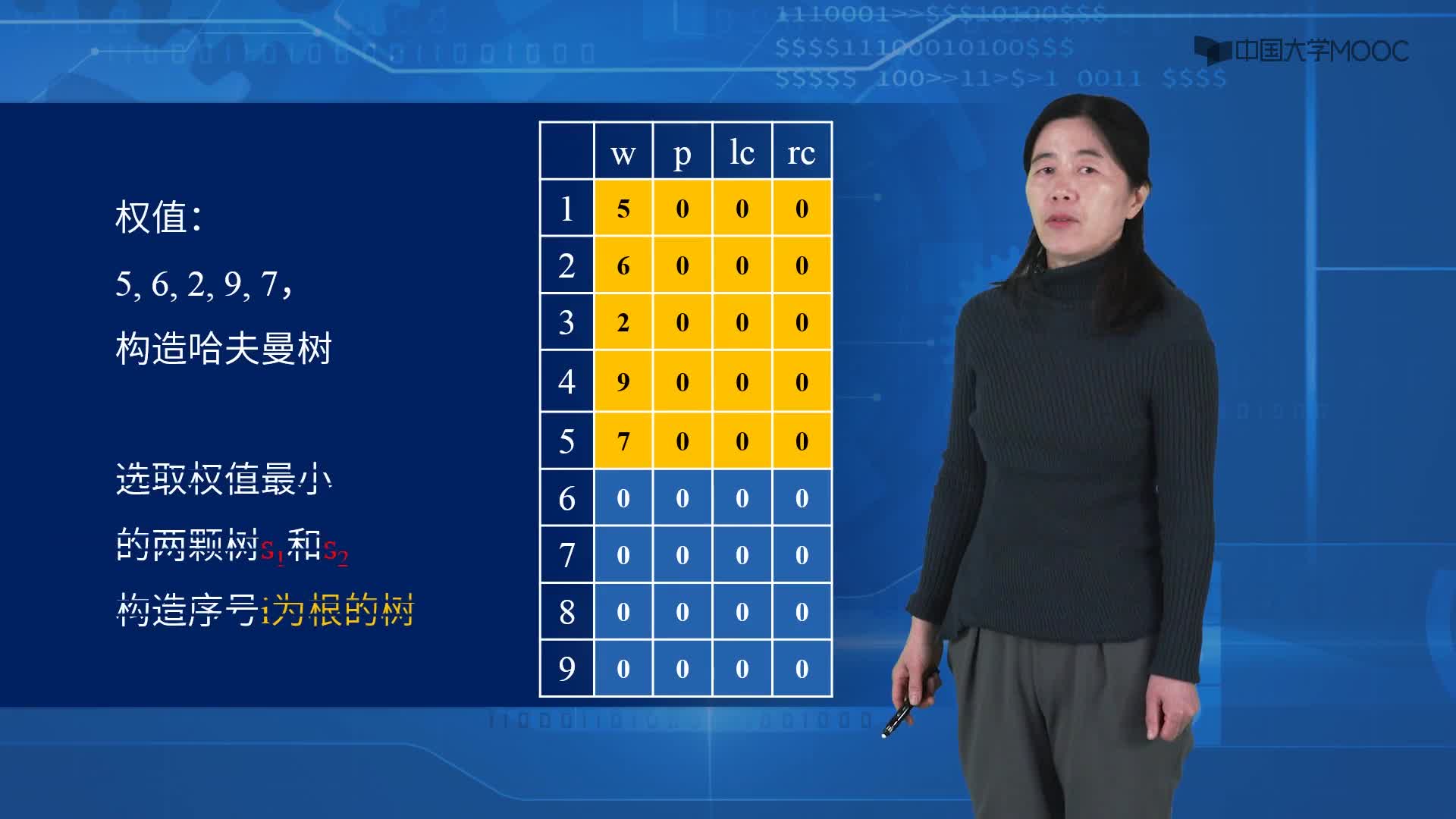
　　1.為每個(gè)符號(hào)建立一個(gè)葉子節(jié)點(diǎn)，并加上其相應(yīng)的發(fā)生頻率

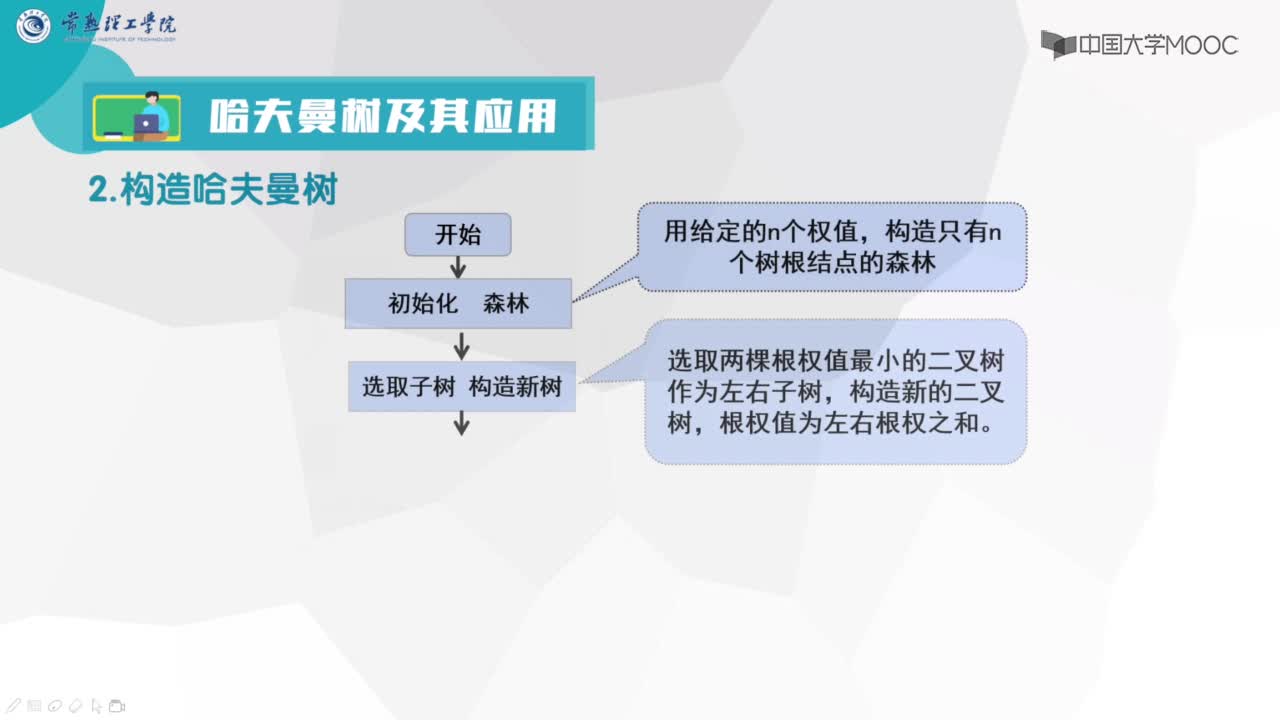
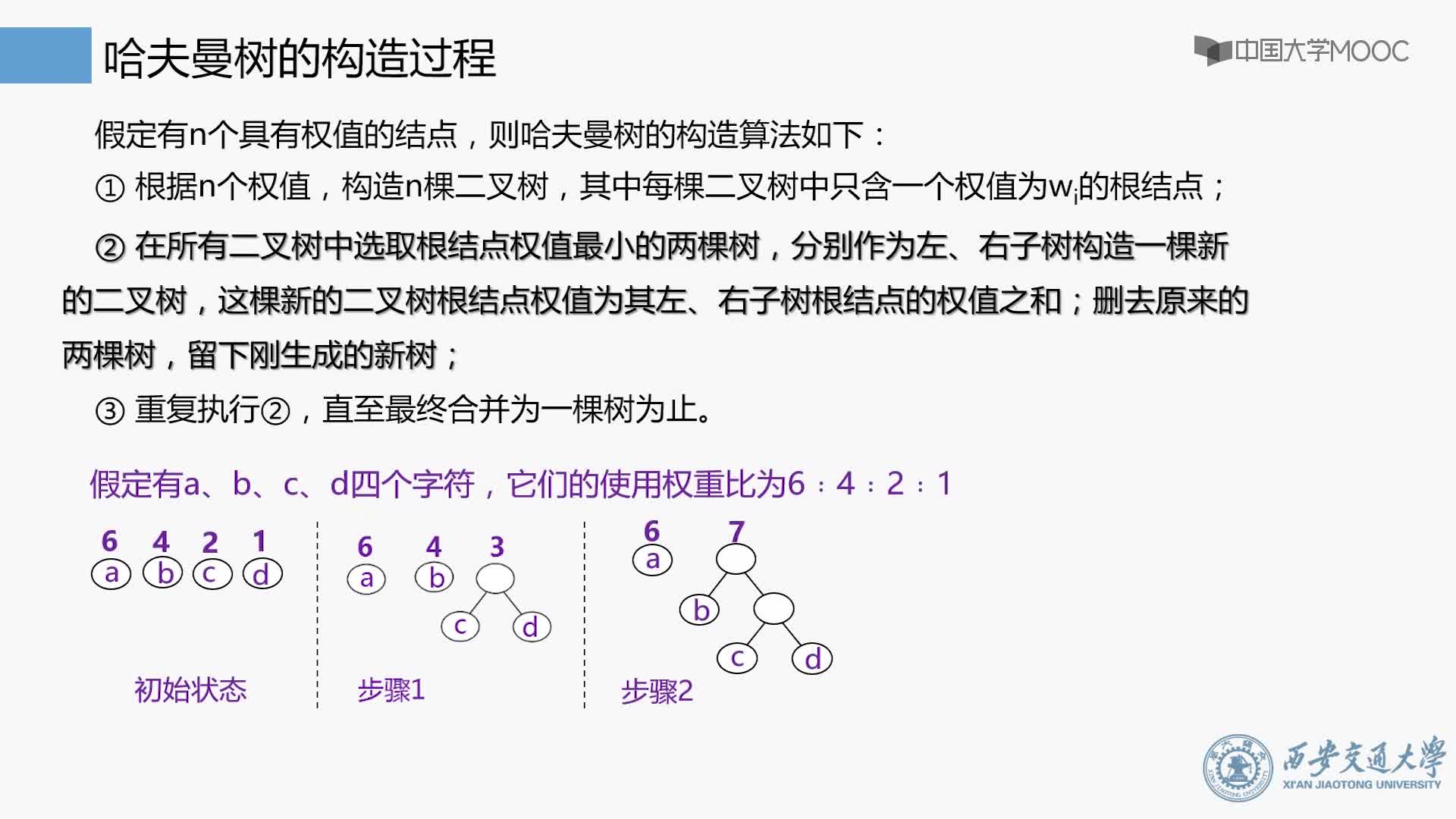
　　2.當(dāng)有一個(gè)以上的節(jié)點(diǎn)存在時(shí)，進(jìn)行下列循環(huán)：

　　1）把這些節(jié)點(diǎn)作為帶權(quán)值的二叉樹的根節(jié)點(diǎn)，左右子樹為空

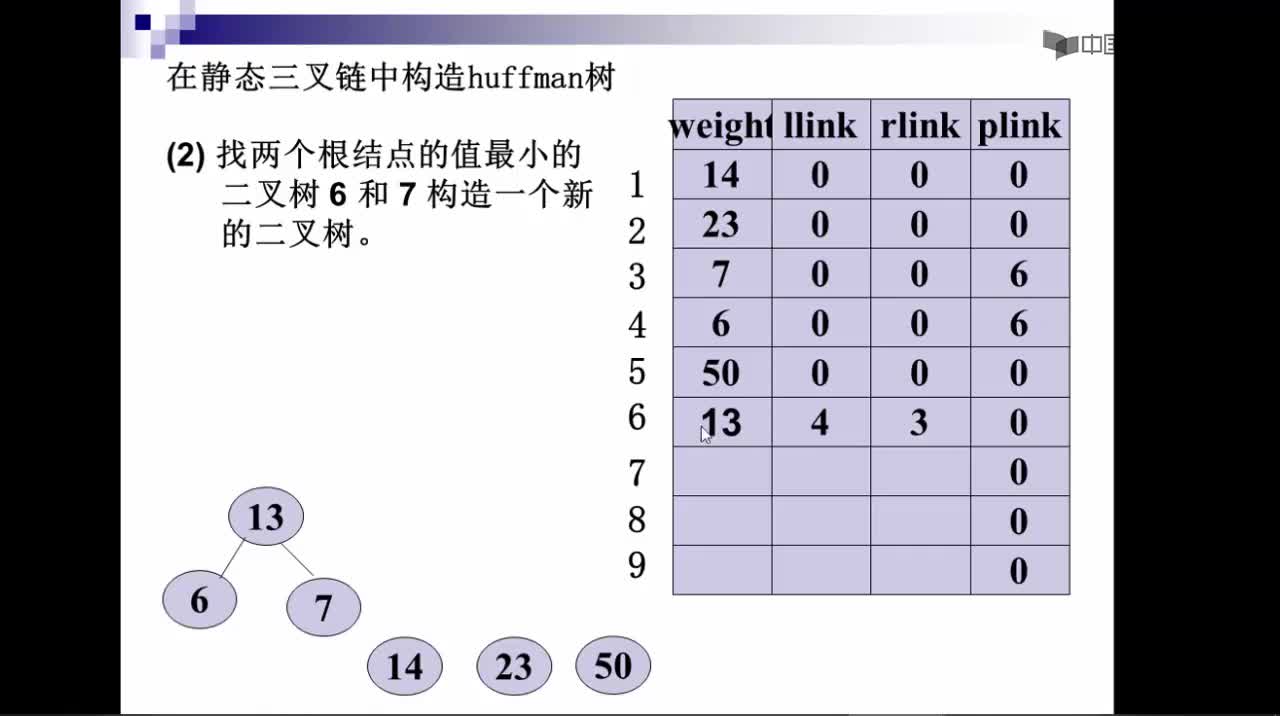
　　2）選擇兩棵根結(jié)點(diǎn)權(quán)值最小的樹作為左右子樹構(gòu)造一棵新的二叉樹，且至新的二叉樹的根結(jié)點(diǎn)的權(quán)值為其左右子樹上根結(jié)點(diǎn)的權(quán)值之和。

　　3）把權(quán)值最小的兩個(gè)根節(jié)點(diǎn)移除

　　4）將新的二叉樹加入隊(duì)列中。

　　5）最后剩下的節(jié)點(diǎn)暨為根節(jié)點(diǎn)，此時(shí)二叉樹已經(jīng)完成。

　　哈夫曼樹的應(yīng)用

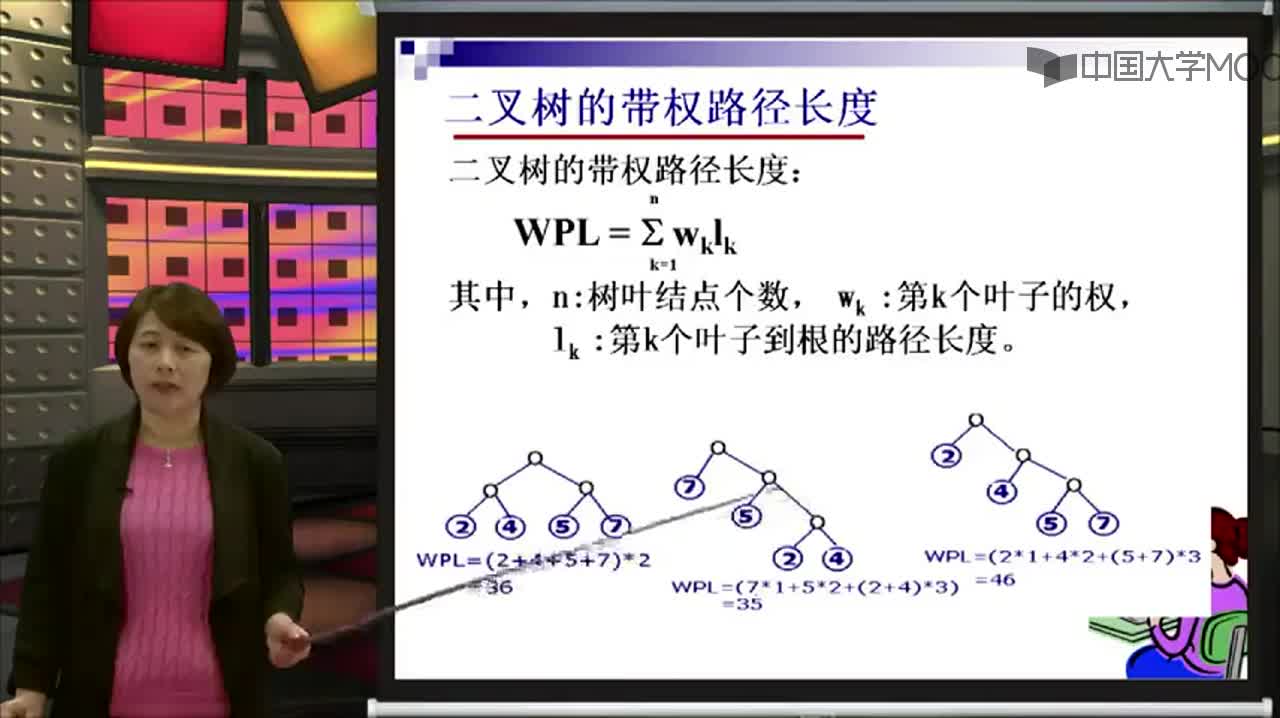
　　哈夫曼編碼：

　　哈夫曼樹可以直接應(yīng)用于通信及數(shù)據(jù)傳送中的二進(jìn)制編碼。設(shè)： D=｛d1，d2，d3…dn｝為需要編碼的字符集合。

　　W=｛w1，w2，w3，…wn｝為D中各字符出現(xiàn)的頻率。現(xiàn)要對(duì)D中的字符進(jìn)行二進(jìn)制編碼，使得：

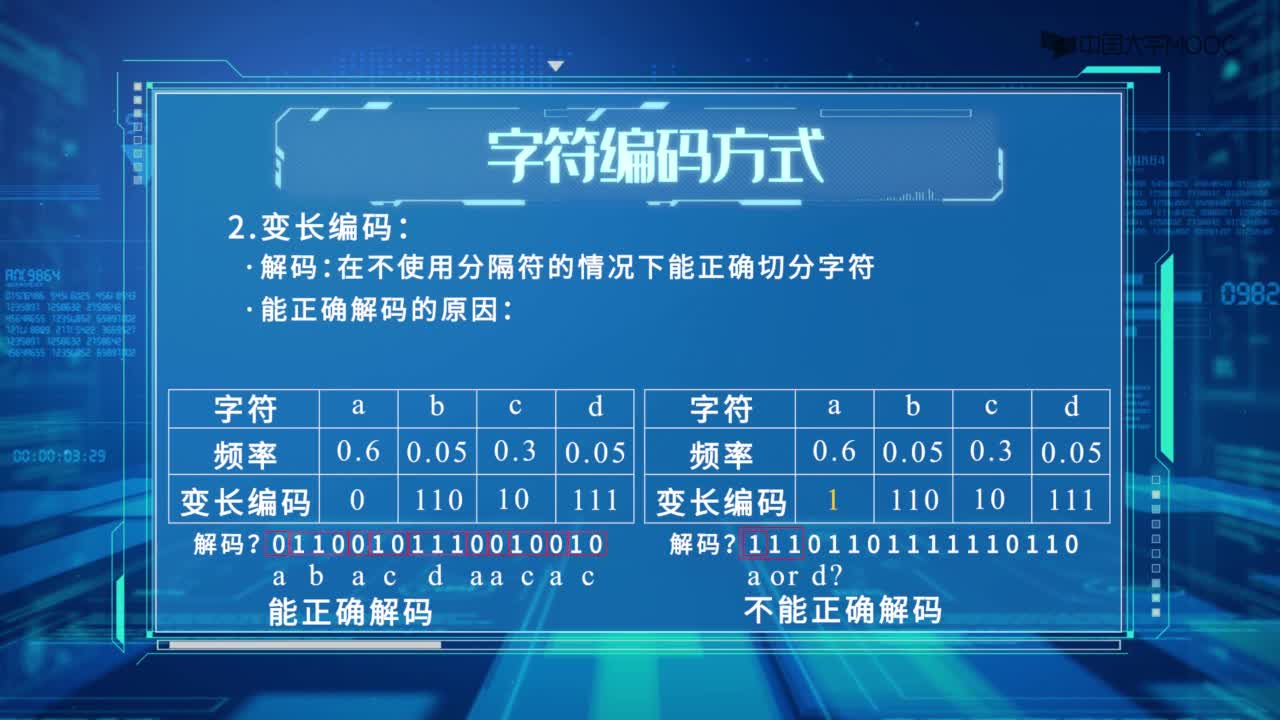
　　（1）按給出的編碼傳輸文件時(shí)，通信編碼的總長(zhǎng)最短。

　　（2）若di不等于dj，則di的編碼不可能是dj的編碼的開始部分（前綴）。

　　滿足上述要求的二進(jìn)制編碼稱為最優(yōu)前綴編碼。上述要求的第一條是為了提高傳輸?shù)乃俣龋诙l是為了保證傳輸?shù)?a target="_blank">信息在譯碼時(shí)無(wú)二性，所以在字符的編碼中間不需要添加任意的分割符。

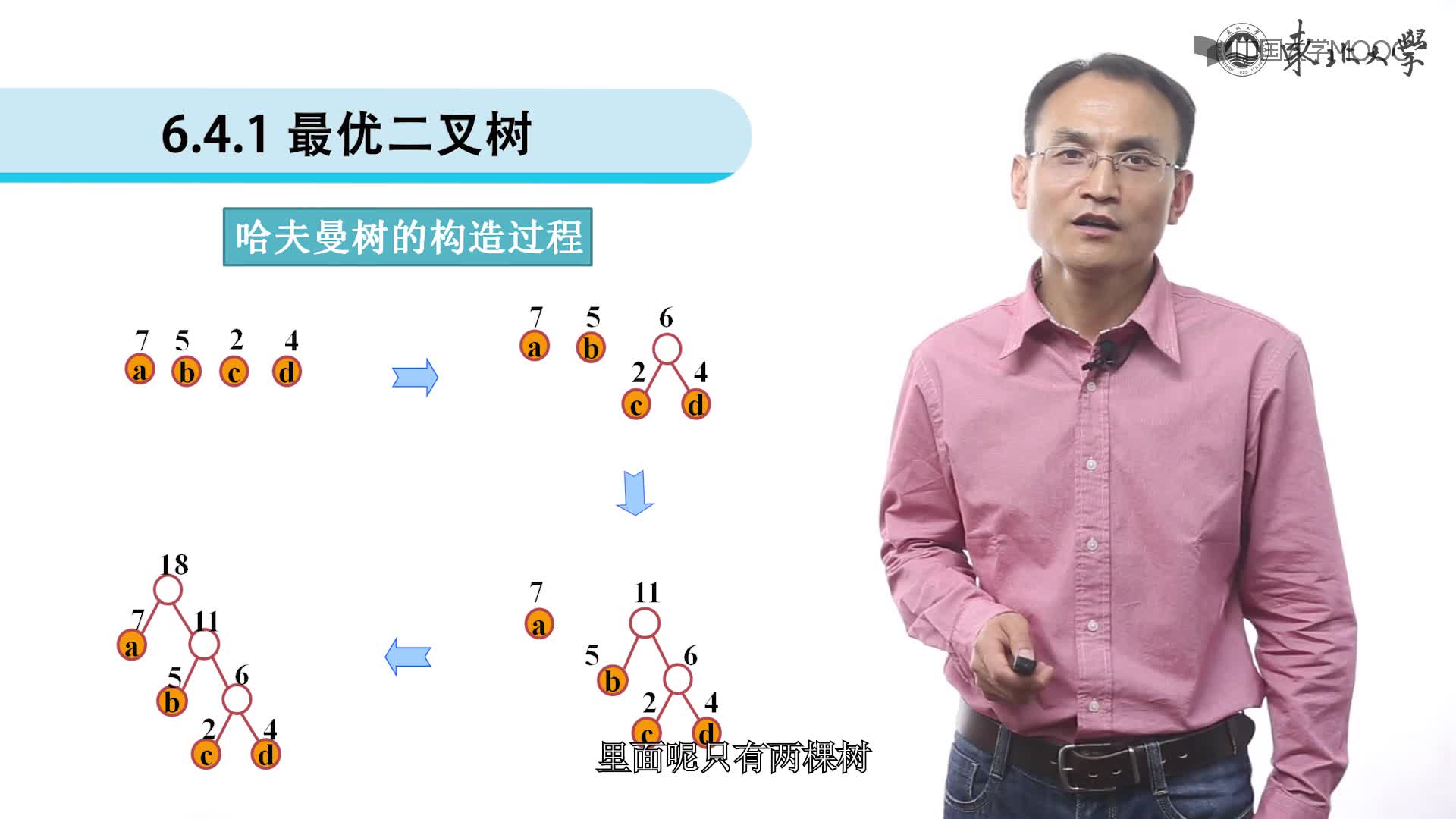
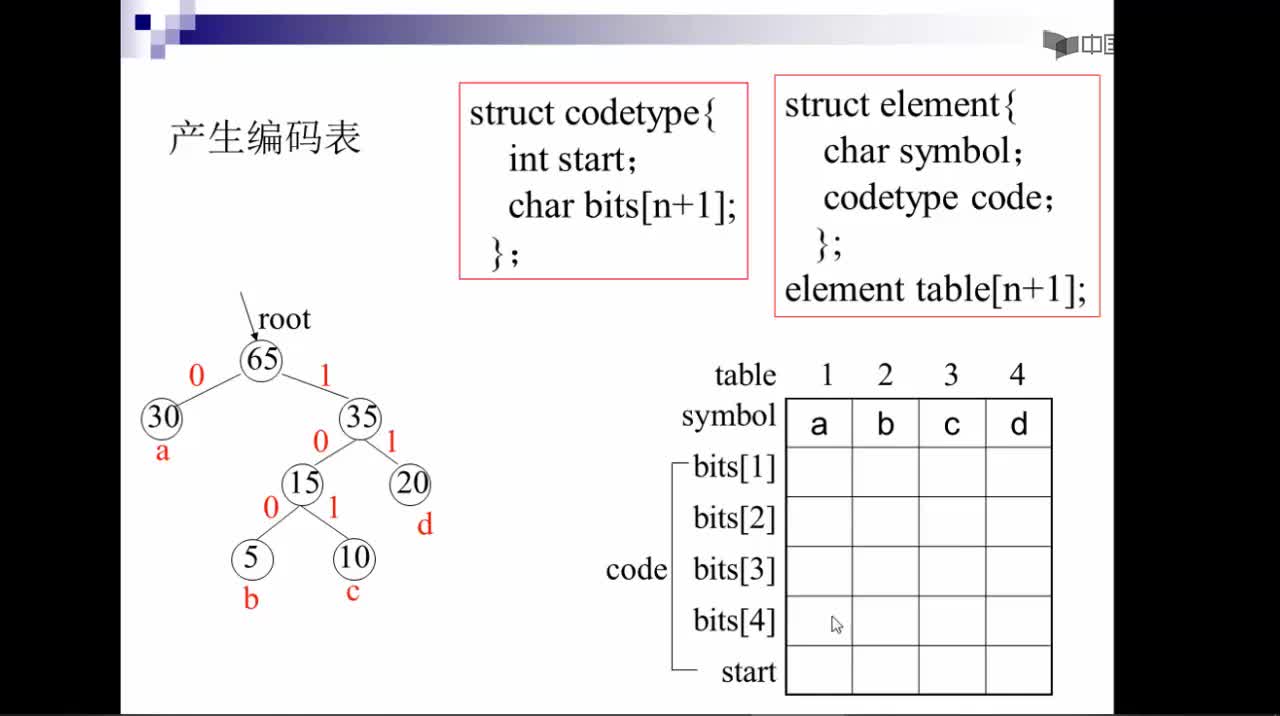
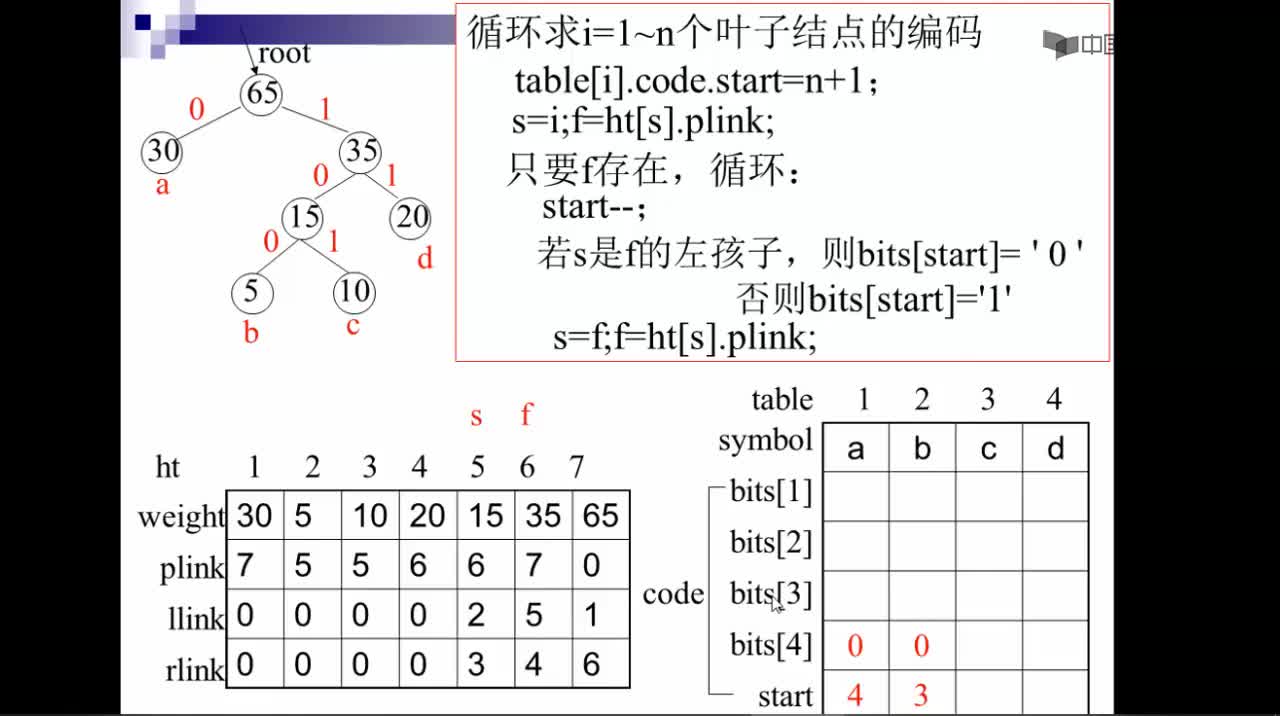
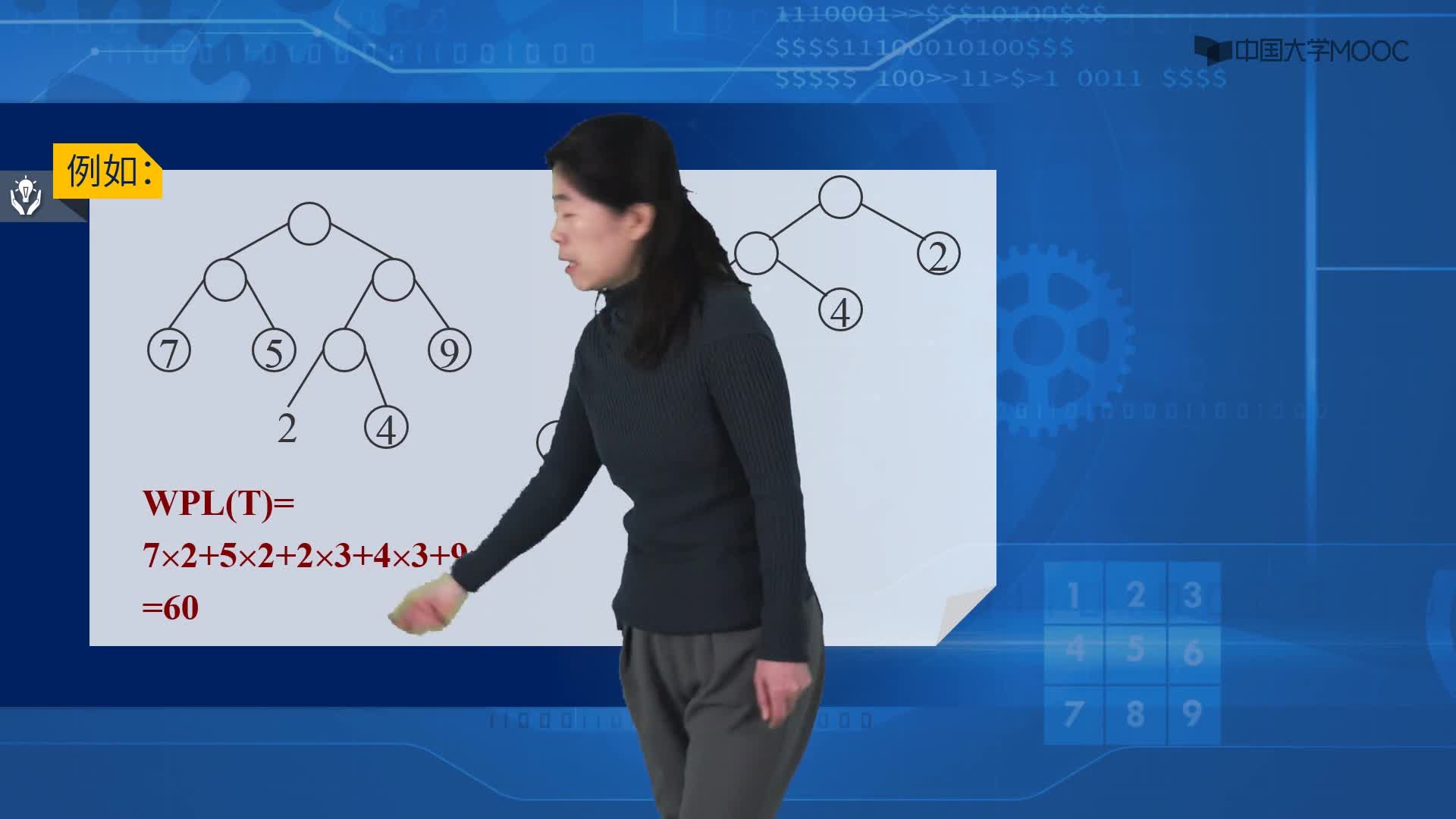
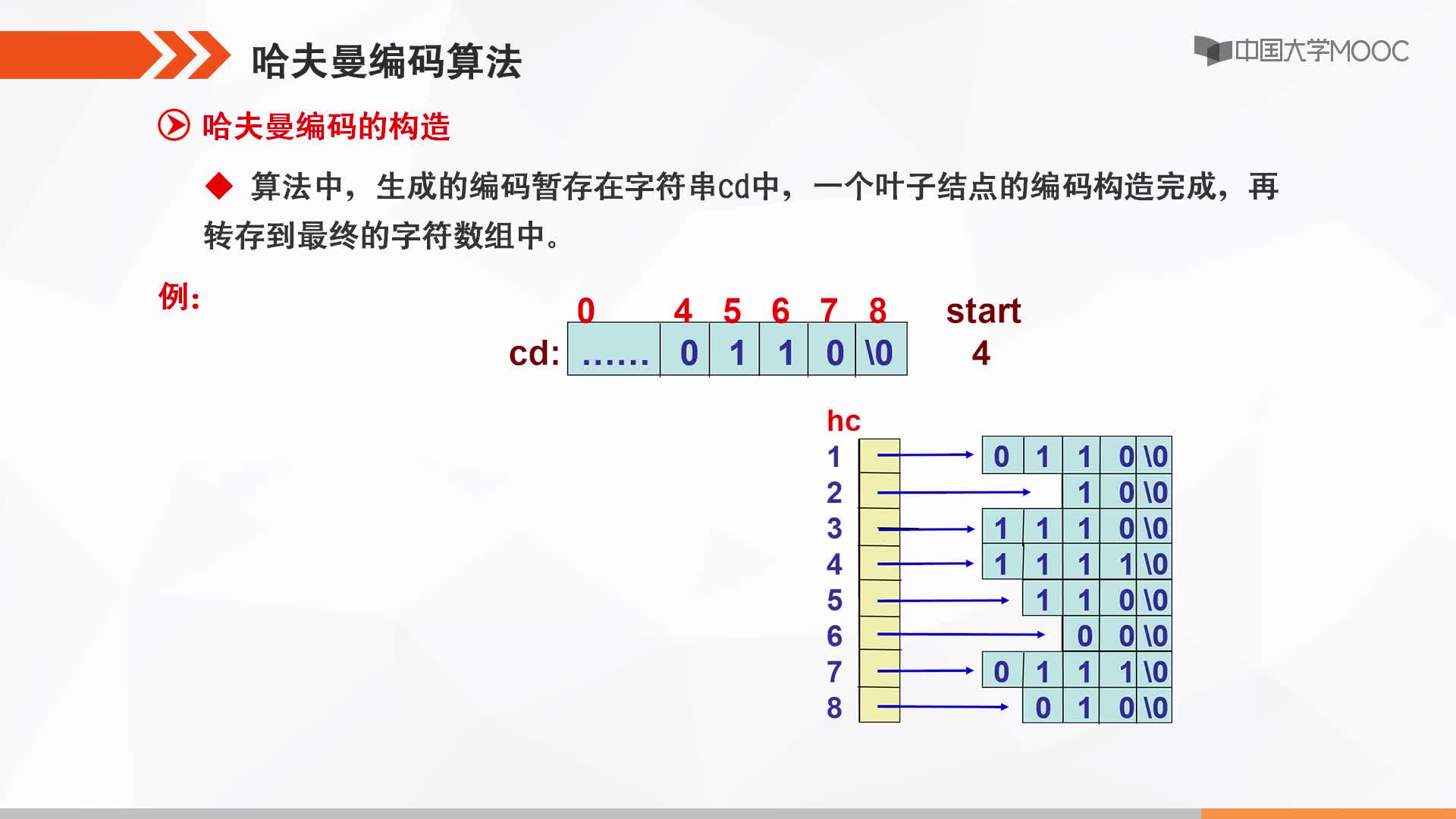
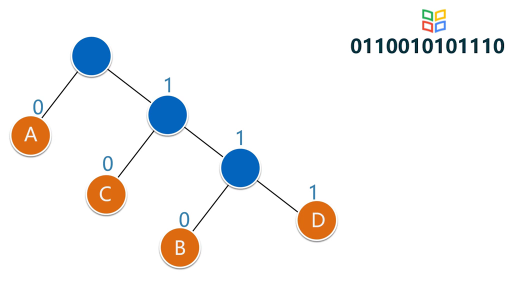
　　對(duì)于這個(gè)問(wèn)題，可以利用哈夫曼樹加以解決：用d1，d2，d3…dn作為外部結(jié)點(diǎn)，用w1，w2，w3…wn作為外部結(jié)點(diǎn)的權(quán)，構(gòu)造哈夫曼樹。在哈夫曼樹中把從每個(gè)結(jié)點(diǎn)引向其左子結(jié)點(diǎn)的邊標(biāo)上二進(jìn)制數(shù)“0”，把從每個(gè)結(jié)點(diǎn)引向右子節(jié)點(diǎn)的邊標(biāo)上二進(jìn)制數(shù)“1”，從根到每個(gè)葉結(jié)點(diǎn)的路徑上的二進(jìn)制數(shù)連接起來(lái)，就是這個(gè)葉結(jié)點(diǎn)所代表字符的最優(yōu)前綴編碼。通常把這種編碼稱為哈夫曼編碼。例如：

　　D=｛d1，d2，d3，d4，d5，d6，d7，d8，d9，d10，d11，d12，d13｝ W=｛2，3，5，7，11，13，17，19，23，29，31，37，41｝利用哈夫曼算法構(gòu)造出如下圖所示的哈夫曼樹：

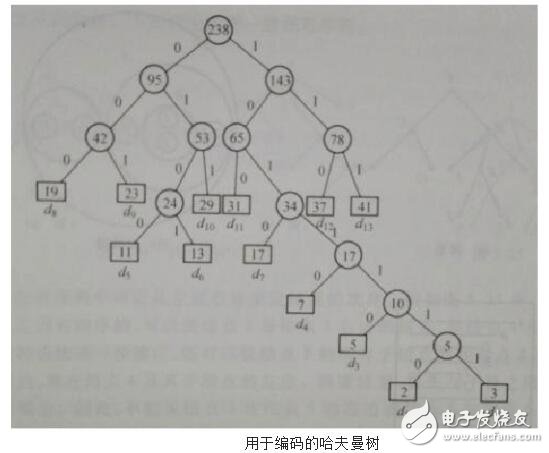
哈夫曼算法的理解及原理分析,構(gòu)造哈夫曼樹的算法