分享本文,希望能起到拋磚引玉的作用,加深朋友對位運算以及計算機底層的認識。
有如下十進制的加法運算:
13 + 9 = 22
我們像這樣來拆分這個運算過程:
不考慮進位,分別對各位數進行相加,結果為sum:
個位數3加上9為2;十位數1加上0為1;最終結果為12;
只考慮進位,結果為carry:
3 + 9 有進位,進位的值為10;
如果步驟2所得進位結果carry不為0,對步驟1所得sum,步驟2所得carry重復步驟1、 2、3;如果carry為0則結束,最終結果為步驟1所得sum:
這里即是對sum = 12 和carry = 10重復以上三個步驟,(a) 不考慮進位,分別對各位數進行相加:sum = 22; (b) 只考慮進位: 上一步沒有進位,所以carry = 0;(c) 步驟2carry = 0,結束,結果為sum = 22。
把上面的運算過程放在二進制中試試。
13和9的二進制分別為:
0000 11010000 1001
①不考慮進位,分別對各位數進行相加得到sum:?
0000 0100
②當考慮進位,有兩處進位,第0位和第3位,只考慮進位的結果為carry:
0001 0010
③判斷carry是否為0,為0則結束,最終計算結果為sum;如果carry不為0,則進行如下操作,并重復步驟①②③:
sum+=carry
上面步驟③中判斷carry不為0,回到步驟①:
不考慮進位,sum+carry= :
0001 0110
步驟②:
只考慮進位,carry =:
0
步驟③:
判斷carry為0,結束,最終sum=:
0001 0110
轉換成十進制剛好是22,十進制的算法同樣適用于二進制!
仔細觀察發現:
第①步不考慮進位的加法其實就是異或運算
第②步只考慮進位就是按位與運算之后左移一位
第③步就是重復前面兩步操作,直到第二步進位結果為0
這里為什么要循環步驟①②③,直到步驟②所得進位carry等于0呢?這是因為有的數做加法時會出現連續進位的情況。在第③步檢測carry如果為0,則表示沒有進位了,此時,此次循環第①步的sum即為最終的結果。
通過位運算實現加法
按照上面的分析,寫出通過位運算實現加法的如下代碼:
// 遞歸寫法 int add(int num1, int num2){if(num2 == 0) return num1;int sum = num1 ^ num2;int carry = (num1 & num2) 《《 1;return add(sum, carry);}
// 迭代寫法 int add(int num1, int num2){ int sum = num1 ^ num2; int carry = (num1 & num2) 《《 1; while(carry != 0){ int a = sum; int b = carry; sum = a ^ b; carry = (a & b) 《《 1; }return sum;}
編輯:lyn
-
C語言
+關注
關注
180文章
7630瀏覽量
140842 -
位運算
+關注
關注
0文章
17瀏覽量
8548
原文標題:通過C語言的位運算實現加法操作
文章出處:【微信號:c-stm32,微信公眾號:STM32嵌入式開發】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
如何用C語言操作寄存器——瑞薩RA系列FSP庫開發實戰指南(10)
Verilog中signed和$signed()的用法
C語言指針運算符詳解
加法運放電路實驗報告數據分析
加法運放電路輸出電壓是多少
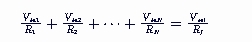





 如何用C語言的位運算實現加法操作詳解
如何用C語言的位運算實現加法操作詳解











評論