01 導論
地球與其它已知星球之最大區別在于地球的表面上存在大量的水。水是生命發生的前提,自然也是物理學發生的前提。水給物理學打上了深深的特征烙印,波(wave)、漲落(fluctuation)、鏡像(mirror image)、渦旋(vortex)等關鍵物理學概念都來自于水。水表面處的分子密度大于體內,其表面張力在20 ℃時~72.75 mN/m,可以說水有一張彈性適中的皮,極易表現出水面的波動。因此,水波也就成為了一個人類也許在有文明之前就爛熟于胸的概念。水波隨處可見,深入人心,也就深入了物理學!
在物理學中,取決于具體的語境,波被用來表示一種運動的形式,也被當作存在的形式,甚至有時不過只是一個空洞抽象的數學表達式。在機械波、電磁波(光波)、物質波(量子力學波函數)以及引力波這些概念中出現的波,以及在傅里葉分析和信號探測理論與實踐中也許是隱性地提及的波,可能多有可檢討的內容。認真分析一下這些波的含義,其所依托概念的來源,其所由來的原初約束與限制,以及其下所依賴的數學,也許可以為對相應的物理學的深刻理解有些許的幫助。
2 機械振動與機械波
固體經歷微小形變時,形變與應力成正比,此即為胡克定律F = -kx ,泰勒展開保證了這個公式的普適性。考察彈簧上一質量為m的振子的振動問題,引入ω2 = k/m ,則振子的運動方程為
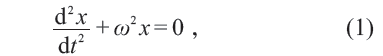
此方程解的形式為
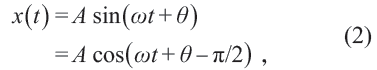
這是一個單變量的三角函數。這即是說,振動在數學上被表示為位置關于時間的三角函數。與此同時,勻速圓周運動可表示為參數方程
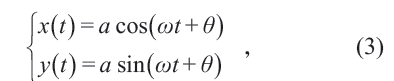
可見勻速轉動在任一方向上的投影是(2)式表述的簡單振動。這說明,振動和轉動實質上有某種一致性。振動與轉動之間的轉換是工業文明的基礎。一個顯見的例子是,縫紉機上踏板的來回振動會轉化為傳動輪的轉動,傳動輪的轉動又轉化為縫紉針的上下振動。縫紉針按照(2)式的諧振動(harmonic oscillation), 配合布料的勻速直線運動,會留下周期性的針腳。
如果振動的物體有足夠的外延,比如一根弦,其上各點的振動之間則可能會是以某種方式耦合的。一根取向沿x 方向的弦的運動方程,在小振幅近似下,為
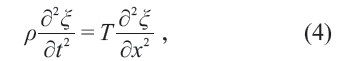
其中ρ 是弦的質量密度,T 是弦(因沿x 方向被緊繃引起)的張力, x ∈[0,L] ,L 是弦長。方程(4)可改寫為
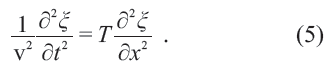
方程(5)形式的關于時間—空間變量的二階微分方程是所謂的經典波動方程。注意,空間變量可以多維的。對于一維情形,方程(5)的通解為
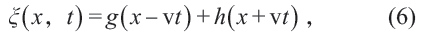
人們把其中形式如
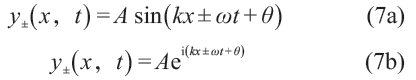
的稱為行波解,其中的k,ω,滿足v = ω/k ,反映的是振動的長度周期和時間周期(一維情形下,k,ω就是兩個數)。注意,弦上的每一點都在與弦垂直的平面內某個方向上振動,所謂的波速v反映的是點振動之間的關聯。實際上,人們也愿意把k,ω看作是實在的物理量,ω是頻率,k 是波矢。波矢,表征波傳播的方向,但實際上它是個切空間里的概念。在三維空間中定義的形如ξ(x,t) = Aei(k ? x - ωt + θ) 的函數,被稱為平面波,意思是波前(wave front)為與方向x垂直的整個平面。平面波展開是常用的計算方法,其合理性和有效性基于傅里葉分析。
(5)式的波動方程和類似(7)式中的表示波的函數,都被當作經典物理中談論波的基礎,甚至成了波的化身,但其實它們遠遠不足以反映機械波的復雜性。比如,1834 年英國人John Scott Russell發現水渠中行駛的船頭總有一個高高的浪頭。此現象涉及的淺水波概念被稱為孤立波。此情景中,水面的運動滿足KdV 方程
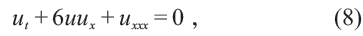
其解的形式為
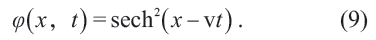
此解與(7)式中的解有相同的本質,是x - vt 形式的變量的三角函數(雙曲函數是虛變量的三角函數)。這反映的是人們數學水平的局限,而非自然現象必然嚴格如此。
3 光的波動說
光充滿宇宙。牛頓認為光是由顆粒(corpuscle)組成的,猜測這可能是來自同雨絲的類比。光線與雨絲一起從夏日的烏云處一起落下,都給人以ray(射線)的印象。雨絲里有一個個的小雨滴,那光線也可能是由分立的顆粒組成的,只是顆粒個頭太小不易分辨而已。荷蘭的惠更斯比較水波的形象和燭光搖曳的影子,認為光應該是水波那樣的波,此為光的波動說。光之波動說的確立有兩個關鍵證據。1801 年英國人托馬斯·楊參照水波干涉所做的光雙縫干涉實驗,得到了如同波浪高低起伏的明暗相間條紋(圖2)。1815 年法國人菲涅爾從惠更斯原理,即波前上的每一點都可以作為次級波源,出發,對楊的實驗結果給出了計算上的證實。菲涅爾的計算還預言,在光路上的圓形小物體,其所造成的陰影中心是亮的。該預言于1817年被實驗觀察證實。
對雙縫干涉實驗的所謂計算解釋,其關鍵詞就是三角函數之和。對函數eikx - ωt + eik(x + Δx) - ωt 求模平方,可得周期函數2 + 2cos kΔx ,干涉條紋的明暗相間就是用這個函數解釋的。當然了,對這個公式不可過于當真,即便計入狹縫的衍射效應所得到的強度分布公式也不能嚴格擬合實驗得到的強度分布,而所謂的干涉花樣強度分布的實驗測量,本身就是個有趣的、困難的話題。
不管怎樣,光的波動說建立起來了。基于波的概念,或者說基于三角函數表示的振蕩及一些其它信念,許多光的現象可以被解釋得相當令人滿意。此時的光是一種波,是某種物質的振動(vibration)。
4 麥克斯韋方程組與電磁波
在1861—1862 年間,英國人麥克斯韋在總結前人電磁學研究的基礎上,得到了一組方程
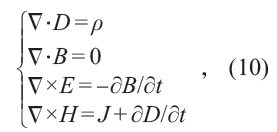
其中第四個方程中的?D/?t 項被稱為位移電流,是麥克斯韋添加上去的。1865 年,麥克斯韋得到了關于電磁場的波動方程
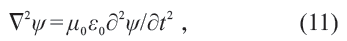
其中的波速c = (μ0ε0)-1/2 具有和當時測得的光速大抵相近的值。這自然導致兩個具有重要物理意義的問題:
1)電磁場可以是波?
2)電磁波的波速等于光速?如果是,這意味著光是電磁波?
記住,對于此時的麥克斯韋,方程(11)描述的電磁波依然是個機械的概念。
1887 年,德國人赫茲用圖3 所示的裝置在電路旁邊的用一根導線連著的兩個鋅球之間引起了電火花,這說明電磁場從線路中溢出來了。這個實驗被看作是第一次產生了電磁波,不過也許同樣重要的是,它第一次讓人們注意到了光電效應。既然實驗產生了電磁波,且速度就是光速,且還存在大量的光—電和電—光效應,認為光是電磁波就是水到渠成的了。
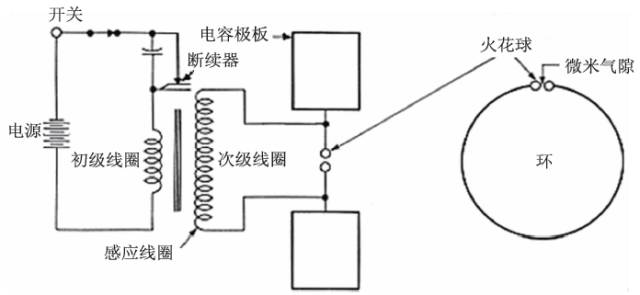
圖3 赫茲產生電磁波所用電路的示意圖
所謂的用電路產生電磁波,電磁波是由電子經加速后向外輻射的。向空間輻射不同花樣的電磁波,要求設計不同樣式的發射天線;當然出于接收電磁波和探測電磁波源的考慮,人們也設計了各色各樣的接收天線。確立電磁波的來源,從來都不是一個簡單的問題。
尋找光,現在是電磁波了,之振動實體或曰介質的過程是物理學史上的重大敘事。Michelson—Morley 實驗的無結果表明,沒有地球對光以太的相對運動。此實驗被當作否定光以太存在的證據。今天的觀點是,電磁波是場,它本身就是存在,它憑借自身向遠處傳播。
5 光的粒子說、物質波與量子力學波函數
1900 年,普朗克從熵概念出發成功擬合了黑體輻射的實驗曲線,其后順著玻爾茲曼的統計物理思路也得到了該擬合曲線。后一條思路用到了一個重要的前提,即頻率為ν的光,其基本能量單位是hν。這是1877 年玻爾茲曼假設的再現。1905 年,愛因斯坦往前更進了一步,他假設如果頻率為ν的光之能量是被固體按照hν一份一份地吸收的,則光電效應的系列實驗結果就能得到完滿的解釋。此外,康普頓研究了電子對X-射線的散射,確立了光的能量量子還對應明確的動量h/λ。到此,原先比照水波概念的光波,有理由被當作粒子(particle)了。注意,此時光是粒子(particle)的觀念同牛頓的光微粒說還是有些區別的:比如,它有明確的頻率或者波長的概念,其能量和動量則分別是固定的hν和h/λ。常數h 被稱為普朗克常數。
光是波還是粒子的觀念激發了法國人德布羅意的靈感:如果光既是(水)波又是粒子,那么作為粒子的電子是否也是波,或者說也會表現出波的行為?1924 年,德布羅意提出了物質波的概念:電子這樣的粒子也是波,相應的波長和頻率由粒子的能量E和動量p給出

1927 年美國人Davidsson 和Germer 用電子束照射到鎳晶體上,獲得了如同X-射線晶體衍射那樣的花樣,算是首次驗證了電子的波動性。
德布羅意的物質波概念隨著他的博士論文被送到了德國和瑞士。據說愛因斯坦對物質波的概念非常欣賞。勞厄認為關于物質波總該有個波動方程,薛定諤接受了為物質波構造方程的挑戰并在1926 年分四部分發表了題為《作為本征值問題的量子力學》的論文,提出了量子力學的波動方程

其中,算符H是系統的哈密頓量,而函數ψ(x,t)是粒子的波函數。波函數是關于時空的復函數,其模平方為粒子在空間某處出現的幾率密度——如果這波函數可以歸一的話。
粒子是波或者會表現出波動行為的想法,結果導致了量子力學以及波函數的概念。根據量子力學,粒子的所有物理信息都被包含在描述其狀態的波函數中了。考察如下的一維諧振子的波函數
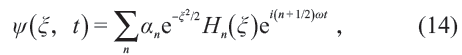
雖然仍可見類似eiωt 那樣的因子,但卻沒有ei(kx - ωt)這樣的因子了。這一點也不妨礙我們把(14)式中的函數稱為波函數。量子力學帶來了物理學的革命,也徹底改變了人類社會,至于其波函數中不(必然)含有ei(kx - ωt) 這樣的描述波動的因子,那有什么關系。波函數到底是什么, 重要嗎?嗯……,不重要嗎?
與對應(7)式那樣的經典平面波表示ψ ∝ ei(kx - ωt)相比,量子力學平面波函數
ψ ∝ ei(p??x?- Et)/?具有更多的內容,其中t 是作為參數的時間,E是體系的能量,對應哈密頓算符H;而x?是位置算符, p?是動量算符,兩者還要滿足量子化條件[x?,p?]=i? ;? = h/2π ,h是普朗克常數,是量子力學的標簽。
量子力學帶來更多的認識。考察一維自由粒子,其哈密頓量為
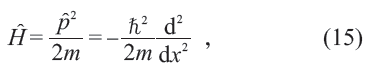
相應的定態薛定諤方程為
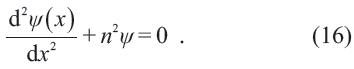
滿足波函數要求的形式解為cos(nx), sin(nx),x ∈(x0,x0 + 2π)。根據量子力學(的數學),此處的哈密頓量是一個自伴隨算符,其所有本征函數構成了一個完備正交基,即是說對于任何定義在(0,2π)上的函數f(x),有
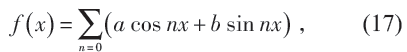
這分明是傅里葉級數展開。
6 傅里葉分析
傅里葉級數是法國人傅里葉在研究傳熱問題時得到的。(17)式形式的展開威力巨大,連鋸齒狀的或者平臺狀的嚴重非光滑函數都可以根據(17)式展開成光滑的三角函數的級數——這個不可思議的特點最是它令人難以接受的地方。進一步地,對于時間的函數s(t),一般有傅里葉變換
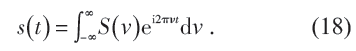
注意,此處與時間共軛的頻率變量也是連續的。
有了傅里葉分析,一般的時空變量的函數f (x,t) 都能表示為sin(kx - ωt) 形式的函數對k,ω的求和或者積分。一條毫無變化的水平線經過傅里葉分析,如果只看其有限的傅里葉展開項,也成了波了,如果波指的是sin(kx - ωt) 形式的三角函數的話。在分析實踐中, 某個時空函數f (x,t) 在固定點上表現為時間序列f (x0,t),它可以按照(18)式被分析為是由具有某頻率譜的波疊加而成的。探測到一個時間序列,將之解釋為對波的探測,除了會作傅里葉分析的功夫,還要有其它的輔助性信念。
傅里葉分析容易讓人想起托勒密的epicycleon-deferent 理論,漢譯本輪—均輪理論。圓周運動上疊加圓周運動是很容易得到各種可能不是很光滑的圖形的,包括棱角分明的三角形——這是數學的威力。
7 相對論與引力波
在牛頓力學中,在引力質量Mg的引力場中運動的質點(慣性質量為mi,引力質量為mg),其運動方程為
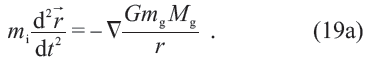
在伽利略變換t ? t′ , r ? r′= r - vt + r0 下,此方程形式不變。與此同時,電磁學的波動方程(11)則是在洛倫茲變換
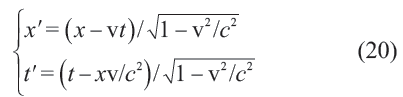
下保持形式不變;或者說,變換(20)保持(光的)時空距離函數
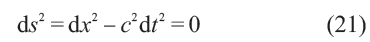
不變。此為狹義相對論。顯然,經典電磁學和引力的方程遵從不同的變換規律,這表明物理學內部尚不協調。愛因斯坦決定把狹義相對論也應用于引力問題,為此要把狹義相對論加以推廣(generalized)。廣義相對論建立在兩個等價原理上。所謂的引力質量與慣性質量等價,是說方程(19a)可以約化為
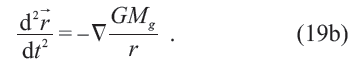
這里方程的左邊是一個運動質點的加速度,右邊則是該質點遭遇的引力場。加上所謂的引力與加速度之間的等價(意思是說19(b)可以移項),而加速度可以從運動軌跡的曲率中得到,因此關于引力的描述就轉化成了關于彎曲時空中路徑之曲率的表述。
愛因斯坦根據以上考慮,從弱靜引力場出發,于1915年構造出了他的引力場方程
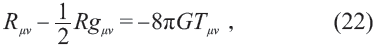
其中gμv 是時空的度規, Rμv 是由gμv 得到的Ricci張量,T 是動量—能量張量。方程(22)于1916 年正式發表,目前只有Schwarzschild 解和Kerr 解這兩個嚴格解,這可能是因為方程(22)要滿足微分同胚協變性,是高度非線性的緣故。與高度非線性的方程(22)相比,經典波動方程和量子力學的薛定諤方程,甚至狄拉克方程,可都是線性的,那里得到的波,或者說(虛)變量x - vt 的三角函數,作為方程的解,還是容易的。
對方程(22)作弱場近似,即考察遠離大質量分布的幾乎平坦的區域,將其度規gμv寫成gμv=ημv+hμv 的形式,其中ημv=(1,1,1;-1)是平直時空(閔可夫斯基時空)的度規,得到近似方程
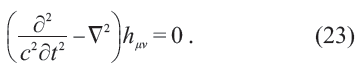
附加的規范條件為h0μ=0;hμμ = 0 ( 橫波, 跡為零)。顯然,(23)和方程(11)具有完全相同的形式,描述的是速度為c 的橫波。此即為引力波方程,此波振蕩的主體是張量hμv=gμv-ημv。或許如同量子力學波函數ψ,hμv也是一個需要詮釋但未被正確詮釋的量。注意,所謂的引力波具有光速的說法,幾乎不具有任何特別的物理意義。愛因斯坦在構造廣義相對論時,本來就是在推廣狹義相對論,要求彎曲時空的局部滿足洛倫茲變換,因此這個參數c 是從一開始被加進去的。如果真有什么獨立的、無心插柳式的實驗,能得到與光速誤差在一兩個數量級內的時空度規振蕩的相速度或群速度,那才真是對廣義相對論的強力支持。
8 結語
本文檢討了自經典力學的機械波到廣義相對論的引力波的諸多波概念。一個事實是,在各種不同語境中出現的波概念,其關切的物理量所涉及的物理現實與數學結構,后者還包括具體方程的形式和波的函數表達,還是有許多或細微或深刻的區別的。在物理學中,波既被當作運動的形式,也被當作存在自身的形式,其實本質上也不過是一個在我們有限的數學知識內容易掌握的工具形式。在真實的物理世界中,一根金屬絲除了會象三角函數那樣來回伸縮,它還會永久變形甚至斷裂;水面上除了有貝塞爾函數那樣的圈狀波紋以及用雙曲函數描述的孤立波,也有能打翻大船的湍流;電磁場除了會優雅地振蕩著飛越真空,它還真能擊穿空氣產生閃電……。物理的現實,不局限于形式簡單的數學解。
審核編輯:郭婷
-
電磁波
+關注
關注
21文章
1481瀏覽量
54611
原文標題:物理學中的波概念
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
吸波材料和屏蔽材料的區別
毫米波雷達工作原理 毫米波雷達應用領域
FMU40-ARB2A4脈沖雷達物位計是電磁波還是機械波
正弦波產生電路有哪幾種
鋸齒波同步信號的觸發電路有哪些
什么是毫米波雷達?毫米波雷達模組選型





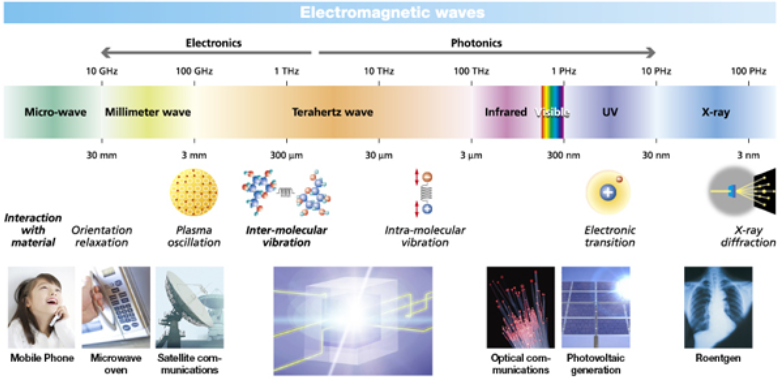
 機械波和引力波的幾種波的概念
機械波和引力波的幾種波的概念











評論