PS:由于本篇文章較長,為了不影響閱讀體驗,所以一分為二,本篇先講述振蕩原理,下一篇再講實際的Snubber電路。
RLC諧振電路廣泛應用于選頻電路中,但由于本人從事非射頻相關工作,所以實際接觸的選頻應用并不多。但是RLC阻尼振蕩卻在平時的電路設計中經常遇到,尤其是與各種電源場合相關的波形振蕩、RC Snubber吸收電路等,其背后的本質都是RLC二階電路動態響應過程的阻尼振蕩。在之前的繼電器和電源文章中都簡單提及到過這個問題,本系列文章將進行詳細講述。
1. RLC振蕩原理
常見的串聯RLC和并聯RLC電路,其原理類似相通,本文以串聯RLC為例進行說明,但并不進行公式推導,而是從結論出發,與實際電路情況進行對應說明。
1.1 零輸入響應
零輸入響應的RLC電路如圖1所示,初始條件為電容電壓UC等于U0,電感電流I等于0,然后開關從左往右撥,根據電路參數的不同,零輸入響應有四種情況:
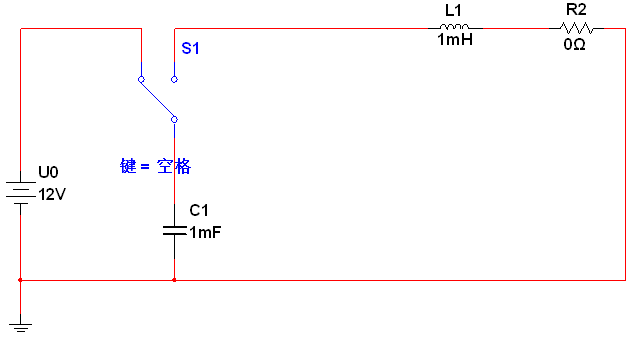
圖1
(1)過阻尼,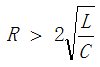 ,電路中的電流在放電過程中永不改變方向,電容在全部時間內一直在非振蕩放電,對應波形示意如圖2所示;
,電路中的電流在放電過程中永不改變方向,電容在全部時間內一直在非振蕩放電,對應波形示意如圖2所示;
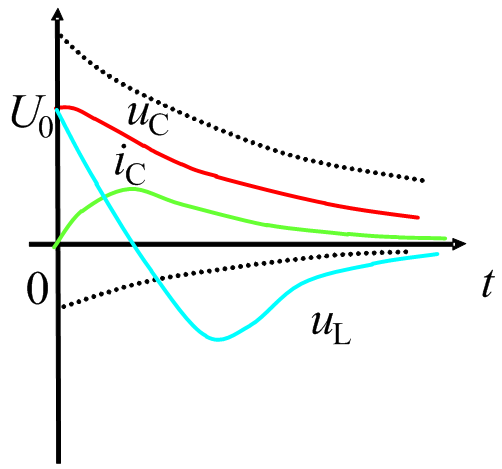
圖2
(2)臨界阻尼,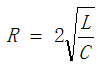 ,電容非振蕩放電,波形與過阻尼類似,如圖2所示;
,電容非振蕩放電,波形與過阻尼類似,如圖2所示;
(3)欠阻尼,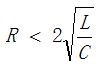 ,電容電壓在零值附近做衰減振蕩放電,電流也在零值附近做衰減振蕩,對應波形示意如圖3所示。這三種有阻尼的情況下,振蕩角頻率為,
,電容電壓在零值附近做衰減振蕩放電,電流也在零值附近做衰減振蕩,對應波形示意如圖3所示。這三種有阻尼的情況下,振蕩角頻率為,
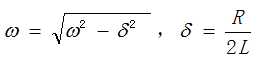
;
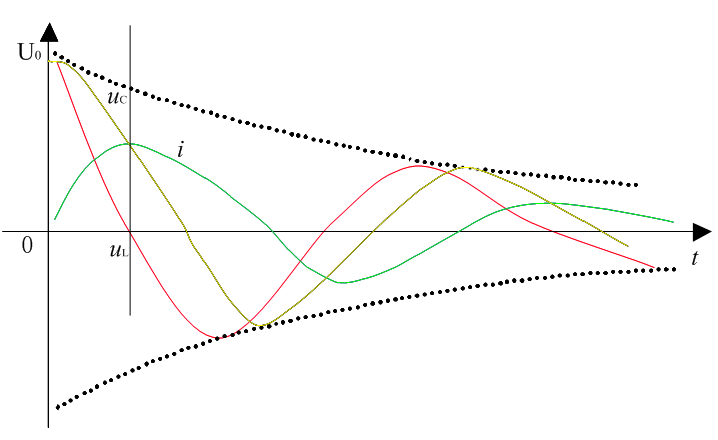
圖3
(4)無阻尼,R=0,電容電壓按正弦規律做等幅振蕩,振蕩角頻率為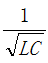 ,對應波形示意如圖4所示,現實情況中阻尼R不可能為0,所以不存在這種現象。
,對應波形示意如圖4所示,現實情況中阻尼R不可能為0,所以不存在這種現象。
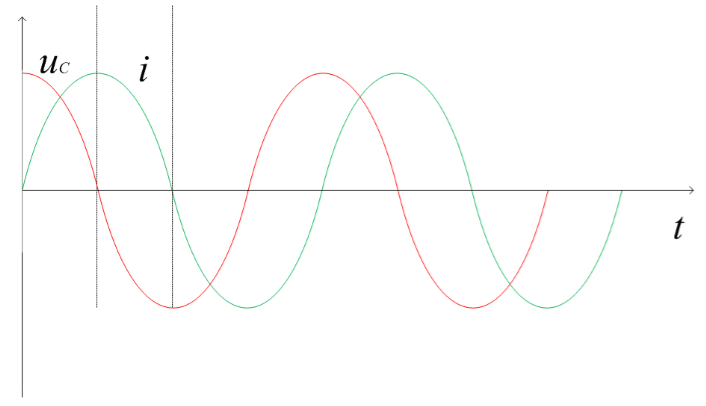
圖4
1.2 零狀態響應
零狀態響應的RLC電路如圖5所示,初始條件為電容電壓UC和電感電流I均等于0,然后輸入激勵。與零輸入響應類似,零狀態響應也有四種情況:
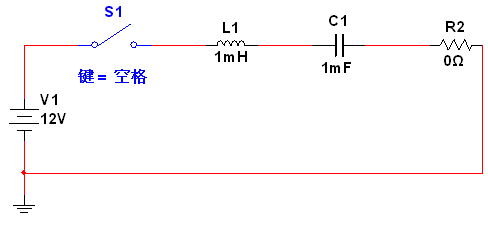
圖5
(1)過阻尼,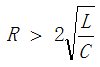 ,電路中的電流在充電過程中永不改變方向,電容在全部時間內一直在非振蕩充電,對應波形示意如圖6所示;
,電路中的電流在充電過程中永不改變方向,電容在全部時間內一直在非振蕩充電,對應波形示意如圖6所示;
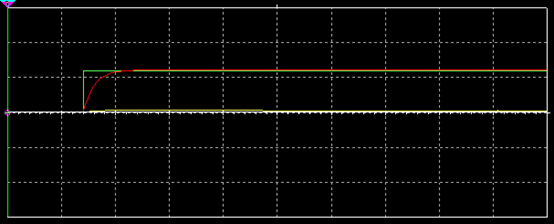
圖6
(2)臨界阻尼,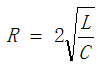 ,電容非振蕩充電,波形與過阻尼類似如圖6所示;
,電容非振蕩充電,波形與過阻尼類似如圖6所示;
(3)欠阻尼,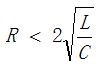 ,電容電壓在電源電壓值U0附近做衰減振蕩充電,但是不會超過電源電壓的2倍,電流在零值附近做衰減振蕩,對應波形如圖7所示。這三種有阻尼的情況下,振蕩角頻率為
,電容電壓在電源電壓值U0附近做衰減振蕩充電,但是不會超過電源電壓的2倍,電流在零值附近做衰減振蕩,對應波形如圖7所示。這三種有阻尼的情況下,振蕩角頻率為
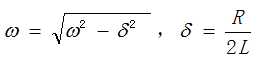
;
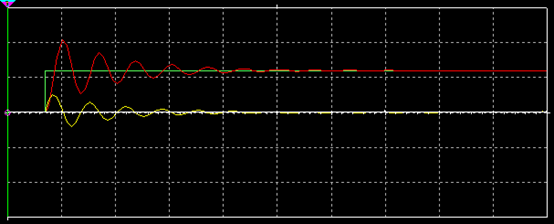
圖7
(4)無阻尼,R=0,電容電壓圍繞著電源電壓值U0按正弦規律在0~2倍的電源電壓大小之間做等幅振蕩,電流圍繞零值附近做等幅的正弦振蕩,振蕩角頻率為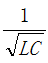 ,對應波形示意如圖8所示,現實情況中阻尼不可能為0,不存在這種現象。
,對應波形示意如圖8所示,現實情況中阻尼不可能為0,不存在這種現象。
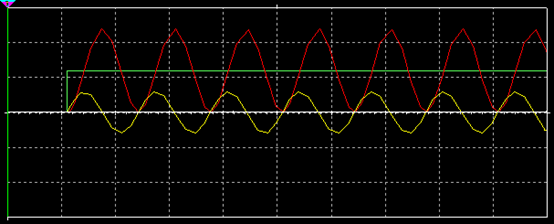
圖8
2. RLC振蕩通俗解釋
上述的阻尼結論是通過數學公式推導得出,波形是通過Multisim仿真得到,但是數學公式并不能讓人對波形圖有直觀的了解,下面將從電荷和電路角度對波形圖進行通俗易懂的解釋。
我們知道電容電壓是連續不能突變的,電容公式I=Cdu/dt,變換可得du=Idt/C,根據數學中的導數知識可得,連續函數在極值點的導數等于0,因此 **電容電壓值最大時** ,即電壓導數du=0時,Idt/C=0,可得 **電容電流I=0** ;同理,電感電流是連續不能突變的,電感公式U=Ldi/dt, **電感電流最大的時候,電感電壓UL=0** 。
2.1 零輸入響應
從無阻尼零輸入響應的波形圖9開始分析,初始條件電容電壓為U0,電感電流為0,由于電阻R=0,由圖1電路,根據基爾霍夫電壓定律可知,無論何時, **電感電壓UL=電容電壓UC** 。在0時刻,由于電容電壓為U0,兩側極板的電荷不平衡,極性為上正下負,所以電容開始放電,電路中的電流開始增加,流向為順時針方向,如圖10所示。直到t1時,電容放電完畢,電壓UC=0,因此電感電壓UL=0。根據上述電感特性,此時電路電流I最大,電容兩側極板電荷處于平衡狀態。 **t1時刻雖然電容處于電荷平衡狀態,但是由于電感電流不能突變,不能瞬間從最大值變為0,只能慢慢降低,這就導致電容的電荷平衡狀態被打破,電容重新被充電,極性與t0時刻相反** **,為上負下正,直至t2時電感電流I=0,根據上述電容特性,此刻電容電壓達到最大值** 。 **t2時刻雖然電感電流I=0,但是此時電容兩側極板的電荷又處于不平衡狀態了,電容又要開始放電,只是方向與0~t1時間段內相反,為逆時針方向,** 后續分析與前述思路相同,不再贅述,整個過程種電容電壓和電流相位正好相差90°。
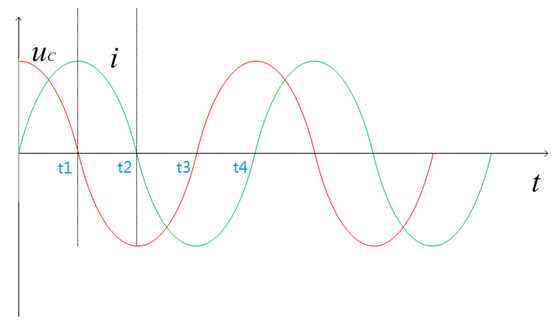
圖9
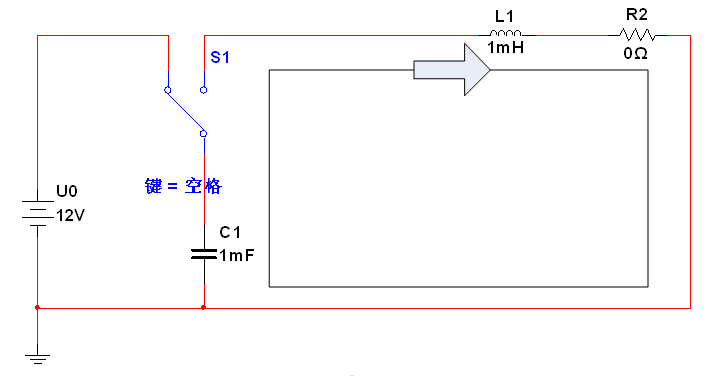
圖10
當電路中的阻尼電阻R≠0時,波形如圖11所示,由于電阻R存在壓降UR,電感電壓UL就不等于電容電壓UC了,而是如下關系:UC=UL+UR。在0時刻,電容放電,電容電壓UC下降,電流I增加,電阻電壓UR增加,直到t1時刻,電容電壓UC和電阻電壓UR相等,即UC=UR=IR時,此時電感電壓UL就等于0,電流I達到最大值,I=UC/R,其小于無阻尼狀態下的電流最大值。t1時刻電容尚未放電完畢,因此在t1~t2時間段內,電容繼續放電直到t2時刻放電結束。而電感電流在t1時刻達到最大值后開始下降,但電流方向不變,到t2時,電容電壓放電完畢,電感電流開始給電容充電,電容極性變為上負下正,直到t3時刻,電感電流I=0,電容電壓UC達到最大值。從分析中可知, **由于電阻R的存在,電感電流在電容尚未放電完畢時就已經達到最大值,電阻R越大,電流最大值I=Uc/R就越小,電流達到最大值的時刻也越早** ,當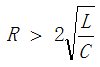 時,電流與電容電壓分別都在同一時刻達到0不再振蕩,形成非振蕩放電。
時,電流與電容電壓分別都在同一時刻達到0不再振蕩,形成非振蕩放電。
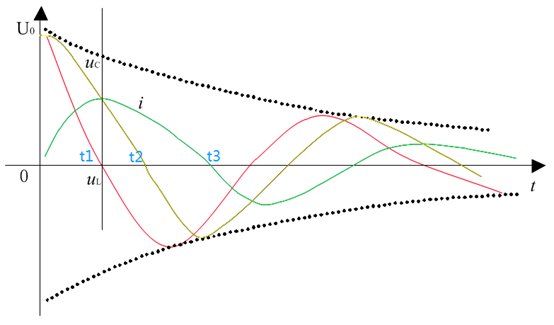
圖11
2.2 零狀態響應
零狀態響應同樣從無阻尼的波形圖12開始分析,初始條件電容電壓UC和電感電流I均為0,激勵電壓為U0,由于電阻R=0,由基爾霍夫電壓定律得,無論何時,U0=UC+UL。在0時刻,電容開始充電,電容UC和電流I開始增加,直到t1時刻,電容電壓UC上升到U0,此時電感電壓UL=0,電感電流I達到最大值。t1時刻后,電流I開始下降,但方向不變,電容繼續充電,直到t2時刻,電流下降到0,電容電壓UC達到最大值2U0。t2時刻后,電容開始放電,電流方向改變為相反方向,電流開始反向增大,直到t3時刻,電容電壓UC下降到U0,此時UL=0,電感電流達到反向最大值。后續分析類似,不再贅述。
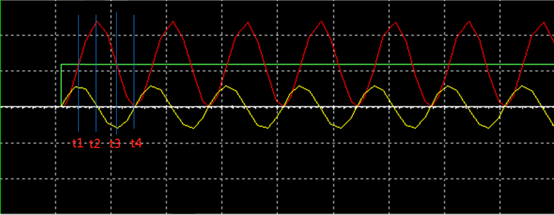
圖12
當電路中的阻尼電阻R≠0時,由于電阻存在壓降,故U0=UR+UC+UL,波形如圖13所示。在0時刻,電容開始充電,電容電壓UC和電流I開始增加,直到t1時刻,U0=UR+UC,UL=0,電流達到最大值I=(U0-UC)/R,小于無阻尼狀態下的電流最大值,此后電感電流開始下降。此時UCU0,電容電壓還未下降到U0。從分析中可知,電阻R越大,電流最大值I=(U0-UC)/R就越小,電流達到最大值的時刻也越早,電容電壓所能達到的最大值也越小,當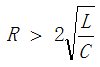 時,電容電壓在電流為0時達到的最大值接近等于U0,由于電容電壓和激勵源U0沒有壓差,無法再充放電,最終形成非振蕩充電。
時,電容電壓在電流為0時達到的最大值接近等于U0,由于電容電壓和激勵源U0沒有壓差,無法再充放電,最終形成非振蕩充電。
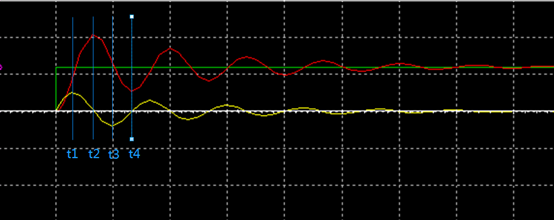
圖13
總結
從前述分析中可知,RLC電路能夠振蕩的初始條件是電容或電感處于不穩定狀態,即電容有充電或者放電的條件,流過電感的電流不為0,最終穩態必然是電容不具備充放電的條件,同時電感電流為0。而振蕩的初始條件在實際的電源電路中經常遇到,這也是隨處可見振蕩的原因,下一篇文章將結合實際電路中的振蕩現象進行講解,并給出如何設計RC吸收電路的參考做法。
-
諧振電路
+關注
關注
11文章
167瀏覽量
27382 -
振蕩
+關注
關注
1文章
134瀏覽量
28537 -
RLC
+關注
關注
1文章
116瀏覽量
39574 -
RLC電路
+關注
關注
2文章
26瀏覽量
7335
發布評論請先 登錄
RLC振蕩電路中如果電容或者電感變化時發生頻移是否可以觀測?
串聯RLC電路的諧振
RLC Network
RLC串聯諧振電路解析,RLC串聯諧振仿真
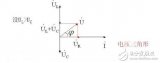





 RLC振蕩原理詳解 RLC振蕩通俗解釋
RLC振蕩原理詳解 RLC振蕩通俗解釋












評論