Labs 導讀
圖作為一種重要的數(shù)據(jù)表示形式,普遍存在于多樣化的實際場景中,如社交網絡中的社交圖、電子商務網站中的用戶興趣圖、科研領域中的論文引文圖等。有效的圖分析能夠幫助人們深入了解數(shù)據(jù)背后的內容,從而解決節(jié)點分類、節(jié)點聚類、鏈路預測等問題。然而圖上的數(shù)學和統(tǒng)計操作是有限的,將機器學習方法直接應用到圖上是很有挑戰(zhàn)性的。在這種情況下,圖嵌入似乎是一個合理的解決方案。
作者:何穎
單位:中國移動智慧家庭運營中心安全產品部
什么是圖嵌入●
圖嵌入是將圖結構數(shù)據(jù)映射為低維稠密向量的過程,同時使得原圖中拓撲結構相似或屬性接近的節(jié)點在向量空間上的位置也接近,能夠很好地解決圖結構數(shù)據(jù)難以高效輸入機器學習算法的問題。
對于圖的表示和存儲,最容易想到的是使用鄰接矩陣的方式。對圖中的每個節(jié)點進行編號,構造出一個 的矩陣,其中
的矩陣,其中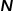 表示圖中節(jié)點的數(shù)量。圖中任意兩個節(jié)點是否有邊相連決定了鄰接矩陣中對應位置的值,這種表示方法非常容易理解且直觀,但是非常低效。因為現(xiàn)實場景中的圖可能會包含成千上萬甚至更多的節(jié)點,而大多數(shù)節(jié)點之間是沒有邊連接的,這會導致得到的鄰接矩陣十分稀疏。使用鄰接矩陣表示和存儲圖需要較高的計算成本和空間成本,而圖嵌入算法能夠高效解決圖分析問題。
表示圖中節(jié)點的數(shù)量。圖中任意兩個節(jié)點是否有邊相連決定了鄰接矩陣中對應位置的值,這種表示方法非常容易理解且直觀,但是非常低效。因為現(xiàn)實場景中的圖可能會包含成千上萬甚至更多的節(jié)點,而大多數(shù)節(jié)點之間是沒有邊連接的,這會導致得到的鄰接矩陣十分稀疏。使用鄰接矩陣表示和存儲圖需要較高的計算成本和空間成本,而圖嵌入算法能夠高效解決圖分析問題。
Part 02 ●基本概念● 概念1 圖: 圖表示為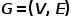 ,其中
,其中 表示節(jié)點,
表示節(jié)點,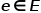 表示邊。
表示邊。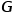 與節(jié)點類型映射函數(shù)
與節(jié)點類型映射函數(shù)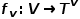 和邊類型映射函數(shù)
和邊類型映射函數(shù)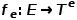 相關聯(lián)。
相關聯(lián)。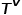 表示節(jié)點類型的集合,
表示節(jié)點類型的集合,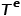 表示邊類型的集合。 ? 概念2 同構圖: 圖
表示邊類型的集合。 ? 概念2 同構圖: 圖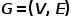 ,其中
,其中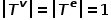 。也就是說,所有節(jié)點都屬于一種類型,所有邊都屬于一種類型,比如社交網絡中的用戶關注關系圖,只有用戶這一種節(jié)點類型和關注關系這一種邊類型。 ? 概念3 異構圖: 圖
。也就是說,所有節(jié)點都屬于一種類型,所有邊都屬于一種類型,比如社交網絡中的用戶關注關系圖,只有用戶這一種節(jié)點類型和關注關系這一種邊類型。 ? 概念3 異構圖: 圖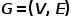 ,其中
,其中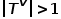 或
或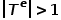 。也就是說,節(jié)點類型或邊類型多于一種,比如學術網絡中的圖結構,存在論文、作者、會議等多種節(jié)點類型,邊的關系包括作者與論文之間的創(chuàng)作關系、論文與會議之間的發(fā)表關系、論文與論文之間的引用關系等。 ? 概念4 一階相似度: 如果連接兩個節(jié)點的邊的權重較大,則它們之間的一階相似度越大。節(jié)點
。也就是說,節(jié)點類型或邊類型多于一種,比如學術網絡中的圖結構,存在論文、作者、會議等多種節(jié)點類型,邊的關系包括作者與論文之間的創(chuàng)作關系、論文與會議之間的發(fā)表關系、論文與論文之間的引用關系等。 ? 概念4 一階相似度: 如果連接兩個節(jié)點的邊的權重較大,則它們之間的一階相似度越大。節(jié)點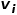 和節(jié)點
和節(jié)點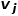 之間的一階相似度表示為
之間的一階相似度表示為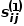 ,有
,有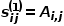 ,其中
,其中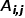 是節(jié)點
是節(jié)點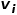 和節(jié)點
和節(jié)點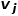 之間連邊
之間連邊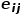 的權重。 ? 概念5 二階相似度: 如果兩個節(jié)點鄰近的網絡結構越相似,則它們之間的二階相似度越大。節(jié)點
的權重。 ? 概念5 二階相似度: 如果兩個節(jié)點鄰近的網絡結構越相似,則它們之間的二階相似度越大。節(jié)點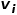 和節(jié)點
和節(jié)點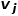 之間的二階相似度
之間的二階相似度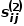 是
是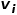 的鄰域
的鄰域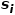 和
和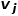 的鄰域
的鄰域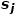 之間的相似性。如圖1所示,因為有邊連接節(jié)點f和節(jié)點g,所以節(jié)點f和節(jié)點g一階相似。雖然沒有邊連接節(jié)點e和節(jié)點g,但是它們相同的鄰居節(jié)點有四個,所以節(jié)點e和節(jié)點g二階相似。 ? ?
之間的相似性。如圖1所示,因為有邊連接節(jié)點f和節(jié)點g,所以節(jié)點f和節(jié)點g一階相似。雖然沒有邊連接節(jié)點e和節(jié)點g,但是它們相同的鄰居節(jié)點有四個,所以節(jié)點e和節(jié)點g二階相似。 ? ?
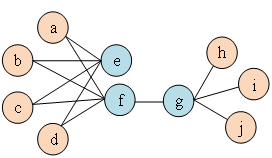
圖1 二階相似度示意圖 概念6 圖嵌入: 給定輸入圖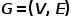 ,以及預定義的嵌入維數(shù)
,以及預定義的嵌入維數(shù)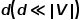 ,圖嵌入是要在盡可能保留圖屬性的前提下,將圖
,圖嵌入是要在盡可能保留圖屬性的前提下,將圖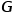 轉換到
轉換到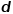 維空間。依賴一階相似度或高階相似度量化圖屬性的保留程度,使用一個
維空間。依賴一階相似度或高階相似度量化圖屬性的保留程度,使用一個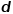 維向量或一組
維向量或一組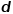 維向量來表示一個圖,每個向量表示圖的一部分的嵌入,例如節(jié)點或邊。
維向量來表示一個圖,每個向量表示圖的一部分的嵌入,例如節(jié)點或邊。
圖嵌入算法分類●
在過去幾十年,研究人員們提出了許多優(yōu)秀的算法,在社交網絡、通信網絡等場景中被證明具有顯著的效果。業(yè)界通常根據(jù)輸出粒度的差異將這些圖嵌入算法分為以下三類:
(1)節(jié)點嵌入
節(jié)點嵌入是最常見的類型,在低維空間中用向量對圖中的每一個節(jié)點進行表示,“相似”節(jié)點的嵌入向量表示也是相似的。當需要對圖中的節(jié)點進行分析,進而執(zhí)行節(jié)點分類或節(jié)點聚類等任務時,通常會選擇節(jié)點嵌入。
(2)邊嵌入
在低維空間中用向量對圖中的每一條邊進行表示。邊由一對節(jié)點組成,通常表示節(jié)點對關系。當需要對圖中的邊進行分析,執(zhí)行知識圖譜關系預測或鏈路預測等任務時,適合選擇邊嵌入。
(3)圖嵌入
在低維空間中用向量對整個圖進行表示,通常是分子或蛋白質這樣的小圖。將圖表示為一個向量便于計算不同圖之間的相似性,從而解決圖分類問題。
不同的任務需求決定了選用的圖嵌入算法,由于篇幅原因,這里節(jié)選出節(jié)點嵌入中的DeepWalk算法和Node2Vec算法來進行相對詳細的學習。
經典圖嵌入算法
● 1.DeepWalk算法 受自然語言處理領域中word2vec思想的啟發(fā),Perozzi等為了建立學習圖中節(jié)點表示向量的模型,將節(jié)點與節(jié)點的共現(xiàn)關系類比于語料庫中詞與詞的共現(xiàn)關系,提出了DeepWalk算法。通過隨機游走的方式采集圖中節(jié)點的鄰居節(jié)點序列,相當于節(jié)點上下文的語料庫,進而可以解決圖中節(jié)點之間共現(xiàn)關系的提取問題。預先設置好節(jié)點序列的長度和起點,隨機游走策略將會指導如何在鄰居節(jié)點中確定下一個游走節(jié)點,重復執(zhí)行該步驟,即可獲得滿足條件的序列,隨機游走示意圖如圖2所示。
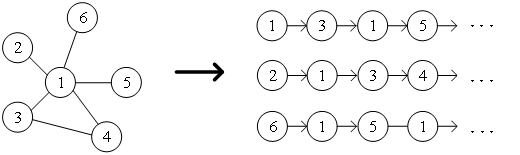
圖2 隨機游走示意圖 將word2vec算法中的單詞對應成圖中的節(jié)點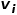 ,單詞序列對應成隨機游走得到的節(jié)點序列,那么對于一個隨機游走
,單詞序列對應成隨機游走得到的節(jié)點序列,那么對于一個隨機游走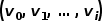 ,定義其優(yōu)化目標函數(shù)如公式所示。 ?
,定義其優(yōu)化目標函數(shù)如公式所示。 ? 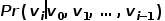 ? 為了更進一步學習節(jié)點的潛在特征表示,DeepWalk算法引入了映射函數(shù)
? 為了更進一步學習節(jié)點的潛在特征表示,DeepWalk算法引入了映射函數(shù)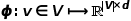 ,實現(xiàn)圖中節(jié)點到
,實現(xiàn)圖中節(jié)點到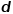 維向量的映射,那么問題就轉換成要估算下列公式的可能性。 ?
維向量的映射,那么問題就轉換成要估算下列公式的可能性。 ? 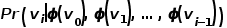 ? 概率的計算同樣需要參考word2vec算法中的skip-gram模型。 ? 如圖3所示,skip-gram模型包含兩個關鍵的矩陣,一個是中心詞向量矩陣
? 概率的計算同樣需要參考word2vec算法中的skip-gram模型。 ? 如圖3所示,skip-gram模型包含兩個關鍵的矩陣,一個是中心詞向量矩陣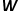 ,另一個是背景詞向量矩陣
,另一個是背景詞向量矩陣 ,這兩個權重矩陣分別代表著作為不同角色時單詞所關聯(lián)的詞向量。skip-gram是一個預測詞上下文的模型,先從語料庫中學習了詞與詞之間的關系,再用這些關系來表達一個特定詞的上下文,即詞的向量表示。也就是說,在同一個序列中,兩個單詞同時出現(xiàn)的頻率越高,兩個單詞的向量表示越相似。將這個思想應用到圖中,定義其優(yōu)化目標函數(shù)如公式所示。 ?
,這兩個權重矩陣分別代表著作為不同角色時單詞所關聯(lián)的詞向量。skip-gram是一個預測詞上下文的模型,先從語料庫中學習了詞與詞之間的關系,再用這些關系來表達一個特定詞的上下文,即詞的向量表示。也就是說,在同一個序列中,兩個單詞同時出現(xiàn)的頻率越高,兩個單詞的向量表示越相似。將這個思想應用到圖中,定義其優(yōu)化目標函數(shù)如公式所示。 ? 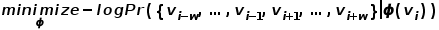 ? 在隨機游走過程中,不考慮采樣序列中節(jié)點與節(jié)點的順序關系,這能夠更好地反映節(jié)點的鄰近關系,同時減少了計算成本。 ?
? 在隨機游走過程中,不考慮采樣序列中節(jié)點與節(jié)點的順序關系,這能夠更好地反映節(jié)點的鄰近關系,同時減少了計算成本。 ?
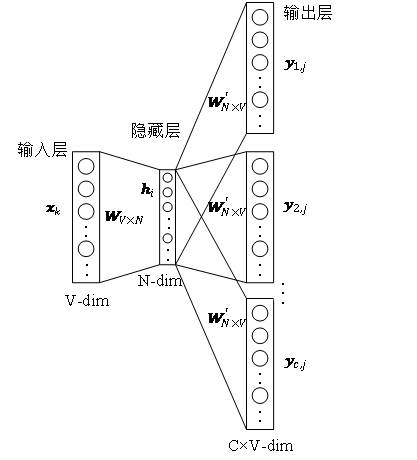
圖3skip-gram模型示意圖 2.Node2Vec算法 在DeepWalk算法的基礎上,研究者Grover A和Leskovec J提出了Node2Vec算法。Node2Vec算法對DeepWalk算法中通過隨機游走生成節(jié)點序列的過程進行優(yōu)化,定義參數(shù)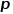 和參數(shù)
和參數(shù)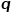 對每次隨機游走是傾向于廣度優(yōu)先采樣還是深度優(yōu)先采樣進行引導,因此適應性很高。假定當前訪問節(jié)點
對每次隨機游走是傾向于廣度優(yōu)先采樣還是深度優(yōu)先采樣進行引導,因此適應性很高。假定當前訪問節(jié)點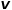 ,則下一個訪問節(jié)點
,則下一個訪問節(jié)點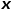 的概率如公式所示。 ?
的概率如公式所示。 ? 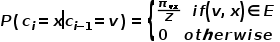 ? 式中
? 式中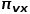 表示從節(jié)點
表示從節(jié)點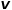 到節(jié)點
到節(jié)點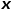 的轉移概率,
的轉移概率,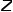 表示歸一化常數(shù)。 ? ?
表示歸一化常數(shù)。 ? ?
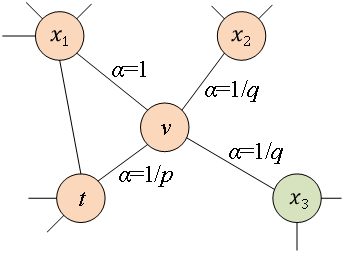
圖4 Node2Vec隨機游走策略示意圖 Node2Vec的隨機游走策略是根據(jù)兩個參數(shù)進行控制的,如圖4所示。假設經過邊 到達節(jié)點v,下一步準備訪問節(jié)點x,設
到達節(jié)點v,下一步準備訪問節(jié)點x,設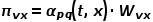 ,
, 是節(jié)點
是節(jié)點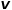 和
和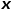 之間的邊權。也就是說,當圖是無權圖時,
之間的邊權。也就是說,當圖是無權圖時,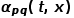 直接決定了節(jié)點的轉移概率。當圖是有權圖時,
直接決定了節(jié)點的轉移概率。當圖是有權圖時,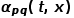 與邊權重的乘積
與邊權重的乘積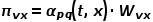 決定了節(jié)點最終的轉移概率。
決定了節(jié)點最終的轉移概率。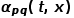 可以根據(jù)以下公式來計算,式中
可以根據(jù)以下公式來計算,式中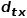 是節(jié)點
是節(jié)點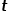 和節(jié)點
和節(jié)點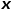 之間的最短路徑距離。 ?
之間的最短路徑距離。 ?
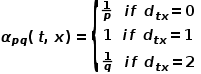
當游走采樣從節(jié)點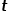 走到節(jié)點
走到節(jié)點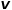 并需要選擇下一跳節(jié)點時,會有以下三種情況。 ? (1) 當
并需要選擇下一跳節(jié)點時,會有以下三種情況。 ? (1) 當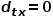 時,返回節(jié)點
時,返回節(jié)點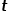 。 ? (2) 當
。 ? (2) 當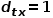 時,選擇節(jié)點
時,選擇節(jié)點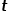 和節(jié)點
和節(jié)點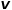 的共同鄰接節(jié)點,例如節(jié)點
的共同鄰接節(jié)點,例如節(jié)點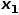 。 ? (3) 當
。 ? (3) 當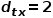 時,選擇與節(jié)點
時,選擇與節(jié)點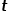 無關的節(jié)點
無關的節(jié)點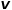 的鄰接節(jié)點,例如節(jié)點
的鄰接節(jié)點,例如節(jié)點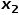 或
或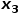 。 ? 也就是說,參數(shù)
。 ? 也就是說,參數(shù)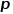 控制著返回上一跳節(jié)點的概率,參數(shù)
控制著返回上一跳節(jié)點的概率,參數(shù)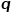 更多地控制的是探索網絡的局部結構信息還是全局結構信息,DeepWalk模型其實是
更多地控制的是探索網絡的局部結構信息還是全局結構信息,DeepWalk模型其實是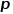 和
和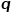 的值設置為1時的Node2Vec模型。
的值設置為1時的Node2Vec模型。
總結
隨著信息技術的快速發(fā)展,網絡環(huán)境變得日益復雜,網絡攻擊頻發(fā),其中APT攻擊呈高發(fā)態(tài)勢,是企業(yè)需要關注的安全問題。事實上,APT攻擊發(fā)生的基本環(huán)境——網絡,本身就是一個由計算機等元素構成的網絡結構,這也不難聯(lián)想到使用圖數(shù)據(jù)結構來表達這些元素間的關系,再將攻擊檢測問題轉化為圖中的節(jié)點、邊或子圖分類任務。圖嵌入是一個豐富且極具研究空間的問題,如何提高模型訓練效率、創(chuàng)新模型構造方法、將圖嵌入的思想應用于更多的生產實踐,企業(yè)需要通過更進一步的研究,才能找到更好的答案。
參考文獻
[1]Xu M. Understanding graph embedding methods and their applications[J]. SIAM Review, 2021, 63(4): 825-853.
[2]Cai H, Zheng VW, Chang K C C. A comprehensive survey of graph embedding: Problems, techniques, and applications[J]. IEEE Transactions on Knowledge and Data Engineering, 2018, 30(9): 1616-1637.
[3]Goyal P, Ferrara E. Graph embedding techniques, applications, and performance: A survey[J]. Knowledge-Based Systems, 2018, 151: 78-94.
編輯:黃飛
-
機器學習
+關注
關注
66文章
8493瀏覽量
134178
原文標題:淺談圖嵌入算法
文章出處:【微信號:5G通信,微信公眾號:5G通信】歡迎添加關注!文章轉載請注明出處。
發(fā)布評論請先 登錄
經典算法大全(51個C語言算法+單片機常用算法+機器學十大算法)
什么是機器學習? 機器學習基礎入門
Spark機器學習庫的各種機器學習算法
機器學習算法分類





 淺談圖嵌入算法如何高效解決輸入機器學習算法的問題
淺談圖嵌入算法如何高效解決輸入機器學習算法的問題










評論