先說答案,這是肯定的,所有遞歸代碼都可以轉為非遞歸代碼。
之所以所有的遞歸都能轉為迭代算法是因為遞歸借助函數調用,函數調用本身就是基于調用棧這種結構實現的,只不過這一切都是自動完成的,我們當然也可以用代碼手動模擬出來。
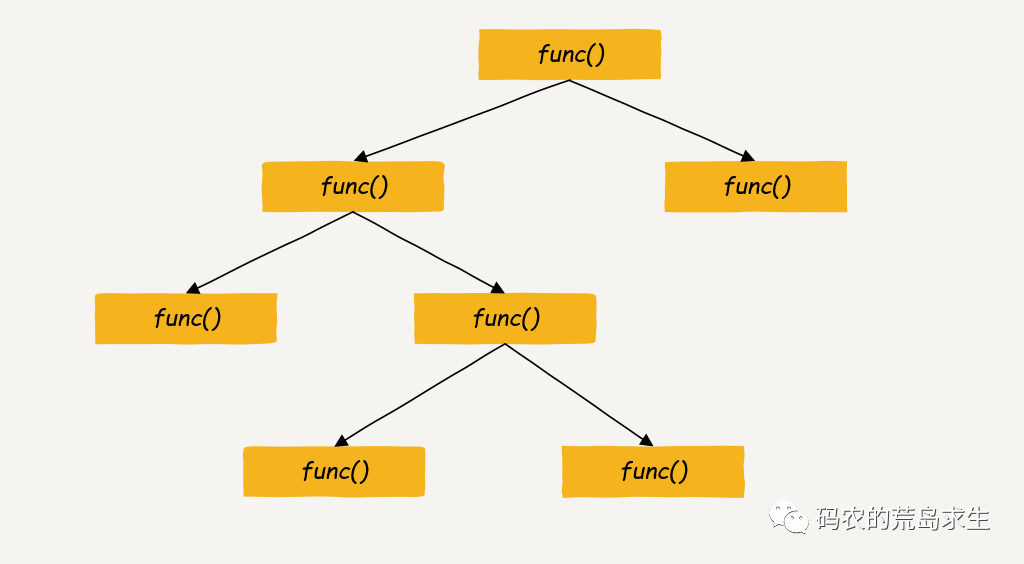
我們知道將遞歸調用全部展開后其實會形成一棵樹,把遞歸轉為非遞歸無非就是在遍歷這棵樹,那么遍歷樹就有很多技術了,基于棧的深度優先遍歷Depth-first traversal,或者基于隊列的廣度優先遍歷breadth-first traversal都是可以的:
說會遞歸轉為非遞歸這個話題,更理論一些的解釋是這樣的,不管是遞歸還是非遞歸,這兩者都是圖靈完備的,既然是圖靈完備,那么它們在表達能力上就是等價的,不存在誰不能轉為誰的問題。
只不過這存在一個難易程度的問題。
大家都知道尾遞歸最容易轉為非遞歸的迭代形式,本質上是這棵樹不是多叉的而是單叉的,單叉的不就退化成鏈表了嘛,遍歷鏈表當然是簡單的,但如果是多叉的話問題就沒那么簡單了, 這里最有趣的是不存在一種模板可以讓我們直接用套路的形式把遞歸轉為非遞歸 ,因此這里存在一個問題:為什么你要把遞歸轉為非遞歸呢?因為最終你會發現將遞歸轉為非遞歸無非就是你自己接手了編譯器本來已經替你完成的工作, 你會發現自己在手動模擬函數調用 。
遞歸的優勢很明顯:代碼簡潔,容易理解和維護,其為人詬病的地方在于執行效率“可能”沒有非遞歸版本的高,但你最好理解這句話到底在說什么,到底哪里效率就不高了?
聲明:本文內容及配圖由入駐作者撰寫或者入駐合作網站授權轉載。文章觀點僅代表作者本人,不代表電子發燒友網立場。文章及其配圖僅供工程師學習之用,如有內容侵權或者其他違規問題,請聯系本站處理。
舉報投訴
相關推薦
關于遞歸,或許在labview中很少聽過或者使用,不過了解下,算是一種娛樂吧,labview是確實支持遞歸的關于遞歸一個可以調用自己的VI就叫做遞歸
發表于 01-05 15:07
("LEVEL %d: n location %p\n" , n, &n);}輸出如下:遞歸的基本原理每級遞歸都使用其私有變量(如例子中的n)每次函數調用都返回前一級(調用他那級
發表于 02-05 20:06
可以用循環替代,但遞歸這種思想符合人類思考問題的方式。在很多問題中,采用遞歸可以大大提高代碼的可讀性,而且編程容易實現。而這時如若非要才要循
發表于 02-14 22:06
我的上一遍主題寫了“三個水桶等分8升水問題”,在其中提到了遞歸的重要性以及LabVIEW如何設置VI才能使得該VI可以實現遞歸調用。而最近看了下《算法的樂趣》中,看到愛因斯坦問題這一章之后,更是讓我
發表于 02-19 11:52
一.NI提供的遞歸調用使用的步驟如下1.將VI設置成重載模式2.使用靜態調用調用調用VI,實現自身調用看見下圖NI自帶遞歸方法二、如果將靜態調用改成直接調用自身也可得到相同的結果,而且程序更直
發表于 05-18 10:36
Labview遞歸函數的使用案例,簡單的1+2+3...+100求和,簡單易懂,充分理解遞歸函數的思想
發表于 10-09 09:37
LabVIEW中使用遞歸算法LabVIEW支持遞歸嗎?如何在LabVIEW中創建遞歸的VI?LabVIEW確實支持遞歸。按照下面的步驟來創建一個遞歸
發表于 04-17 20:11
文中提出一種通用遞歸算法的設計模式,并結合實例說明該模式的應用方法和有效性,為研究遞歸算法提供了有效的解決方案,可推廣性強。同時給出了遞歸程序在調試過程中的一些方法和
發表于 11-03 15:04
?24次下載
LabVIEW中使用遞歸調用不是很方便。并且遞歸并不是編程必須程序結構,任何需要使用遞歸調用的地方,都可以用循環結構來代替。但是在某些情況下,使用遞
發表于 03-25 16:39
?2次下載
之所以所有的遞歸都能轉為迭代算法是因為遞歸借助函數調用,函數調用本身就是基于調用棧這種結構實現的,只不過這一切都是自動完成的,我們當然也可以用代碼
![的頭像]() 發表于
發表于 04-19 15:02
?2181次閱讀
那么我通過一道簡單的面試題,模擬面試的場景,來帶大家逐步分析遞歸算法的時間復雜度,最后找出最優解,來看看同樣是遞歸,怎么就寫成了O(n)的代碼。
![的頭像]() 發表于
發表于 07-13 11:30
?2315次閱讀
Python支持遞歸函數——即直接或間接地調用自身以進行循環的函數。遞歸是頗為高級的話題,并且它在Python中相對少見。然而,它是一項應該了解的有用的技術,因為它允許程序遍歷擁有任意的、不可預知的形狀的結構。遞歸甚至是簡單循環
![的頭像]() 發表于
發表于 02-21 14:28
?681次閱讀
與原問題相似的規模較小的問題來解決,遞歸策略只需少量的程序就可描述出解題過程所需的多次重復計算,大大地減少了程序的代碼量。
![的頭像]() 發表于
發表于 02-21 15:57
?626次閱讀
要說到遞歸如果不說棧的話,我覺得有點不合適,遞歸特點就是不斷的調用同一個函數,如果這個函數沒有一個遞歸界限,那么就是死循環了,所以討論遞歸,就必須要討論
![的頭像]() 發表于
發表于 06-06 15:24
?1072次閱讀
當我們碰到諸如需要求階乘或斐波那契數列的問題時,使用普通的循環往往比較麻煩,但如果我們使用遞歸時,會簡單許多,起到事半功倍的效果。這篇文章主要和大家分享一些和遞歸有關的經典案例,結合一些資料談一下個人的理解,也借此加深自己對遞歸
![的頭像]() 發表于
發表于 08-05 15:57
?393次閱讀








 遞歸代碼都轉為非遞歸可以嗎
遞歸代碼都轉為非遞歸可以嗎











評論